一种测量标记结构的方法、装置及系统与流程

本发明涉及测量标记结构领域，具体涉及测量标记结构的方法、装置及系统。

背景技术：

根据极紫外光刻技术路线图，随着光刻图形cd尺寸进入到7nm及以下工艺节点，对于套刻和cd均匀性要求进一步提升。为了获得预期的套刻精度和线宽均匀性，需要在硅片上加工一批特殊的标记结构，测量该结构，获得套刻精度和cd均匀性，并进一步调制光刻系统的曝光参数，实现对套刻和线宽均匀性的控制。同时，在对准系统和套刻系统中，由于标记的非理想化导致对准误差和套刻误差，也需要测量对准标记的结构。

在测量标记结构时，扫描电子显微镜、原子力显微镜虽然测量分辨率高，但是由于测量速度较慢、测量环境要求苛刻、破坏性等问题，不适用于在线测量；而散射测量的方式由于测量速度较快，分辨率较高的特点成为标记结构在线测量的主要方式。目前采用的散射测量方法主要有角谱散射测量方法和相干傅里叶散射测量方法。其中角谱散射测量方法采用宽谱光源，通过测量不同波长的傅里叶面角谱信息来获得对准结构，但是为了防止不同波长衍射级次的重叠，限制了收集镜组数值孔径，只让0级反射光通过，没有高衍射级次的测量信号；而相干傅里叶散射测量方法，虽然收集镜组数值孔径达到0.95可以收集高衍射级次的衍射光束，但为了保证各衍射级在傅里叶面上相互重叠干涉，测量光束的na较大，导致测量光学系统波像差对测量结果影响较大。因此为了减小波像差的影响，傅里叶相干散色测量方法需要采用哈特曼传感器测量光学系统的波像差。

因此，如何兼顾多衍射级次和光学系统波像差的影响两方面的因素来测量标记结构是目前研究人员关注的问题。

技术实现要素：

(一)要解决的技术问题

如何兼顾多衍射级次和光学系统波像差的影响两方面的因素来测量标记结构是目前研究人员关注的问题。

(二)技术方案

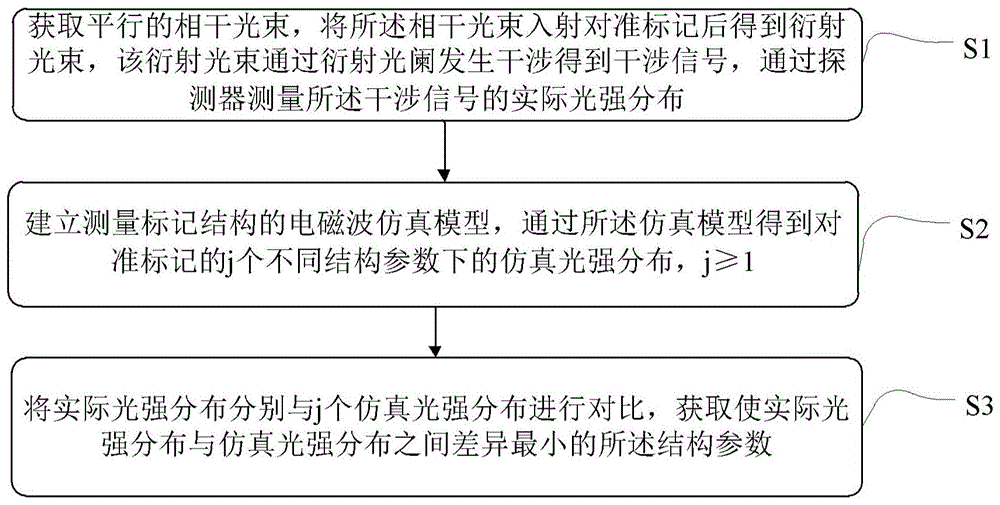
为了解决上述问题，本发明一方面提供了一种测量标记结构的方法，所述方法包括：s1，获取平行的相干光束，将所述相干光束入射对准标记后得到衍射光束，该衍射光束通过衍射光阑发生干涉得到干涉信号，通过探测器测量所述干涉信号的实际光强分布；s2，建立测量标记结构的电磁波仿真模型，通过所述仿真模型得到对准标记的i个不同结构参数下的仿真光强分布，j≥1；s3，将实际光强分布分别与j个仿真光强分布进行对比，获取使实际光强分布与仿真光强分布之间差异最小的所述结构参数。

可选地，所述实际光强分布通过下式表示：

其中，n、m均为对准标记的衍射级次；en、em分别为衍射级级次的复振幅；和为由对准标记结构决定的相位，t(kx)为衍射光阑透射函数t(x)的傅里叶变换，kn、km为衍射级次透过衍射光阑的波矢，由散射测量系统放大倍率以及衍射级次的衍射角决定；kx为阵列探测器上不同位置处波矢的x方向分量，由探测器的位置以及测量光的波矢决定。

可选地，所述s3包括：将实际光强分布分别与j个仿真光强分布进行对比，获取使评价函数值最小的所述结构参数。

所述评价函数通过下式表示：

其中，ii(ω，α)为实际光强分布，α为实际光强分布对应的实际结构参数，为第j个仿真光强分布，αj为第j个仿真光强分布对应的仿真结构参数；ω为散射测量系统中的系统参数，i为空间阵列探测器的像素。

可选地，所述s3包括：s301，将实际光强分布与仿真光强分布进行对比，获取使所述评价函数值最小的第一结构参数；s302，通过非线性优化算法将所述第一结构参数进行优化得到第二结构参数；s303，利用第二结构参数通过电磁波仿真模型，获取优化结构参数后的仿真光强分布；s304，重复步骤s301-s303，直至所述评价函数收敛，得到使实际光强分布与仿真光强分布之间差异最小的所述结构参数。

可选地，所述非线性优化算法为差分迭代算法。

可选地，所述获取平行的相干光束包括：辐射光源产生的光束依次通过准直系统和孔径为300-400μm的孔径光阑后得到所述平行的相干光束。

本发明另一方面提供了一种测量标记结构的散射装置，所述装置包括：依次排布的辐射光源、准直系统、孔径光阑，设置于所述孔径光阑之后的照明镜组和分光镜，分别设置于所述分光镜两侧的收集镜组和聚焦镜组，以及依次设置于所述聚焦镜组之后的衍射光阑和探测器。

可选地，所述探测器为阵列探测器，所述孔径光阑的孔径为300-400μm。

本发明另一方面还提供了一种测量标记结构的系统，所述系统包括上文所述的散射装置，还包括：实际光强分布获取模块，用于通过散射装置获取对准标记的实际光强分布；仿真光强分布获取模块，用于建立测量标记结构的电磁波仿真模型，通过所述仿真模型得到对准标记的j个不同结构参数下的仿真光强分布，j≥1；结构参数获取模块，用于将实际光强分布分别与j个仿真光强分布进行对比，获取使实际光强分布与仿真光强分布之间差异最小的所述结构参数。

(三)有益效果

本公开至少具有以下有益效果：

(1)本发明提供的测量标记结构的装置可以兼顾多衍射级次和光学系统波像差的影响两方面的因素。在发明中采用小尺寸平行相干光束照射对准标记，减小测量系统波像差对测量结果的影响；而采用小尺寸平行相干光束导致对准标记衍射光束在傅里叶面上不重叠，没有干涉信号。为了保证多衍射级次重叠产生干涉信号，引入衍射光阑，使各衍射光束通过光阑衍射扩大其空间范围，相互重叠，产生高衍射级次干涉信号。本发明提供的散射测量装置采用了高衍射级次测量信号，同时减小照明镜组和收集镜组光学系统的影响，提高重建标记结构的测量精度。

(2)本发明提供的测量标记结构的方法和系统，采用上述测量装置提高测量精度的情况下，还利用电磁波仿真模型对进行仿真，通过实际值与仿真值进行对比，寻找使实际值与仿真值差异最小的结构参数。实现了精确获得对准标记结构参数的目的。

附图说明

图1是本发明实施例提供的测量标记结构的方法流程图；

图2是本发明的实施例提供的测量标记结构装置结构示意图；

图3是本发明的实施例提供对准标记结构示意图；

图4是本发明的实施例提供的测量标记结构的方法中各衍射级在收集镜头傅里叶面上光斑分布示意图；

图5是本发明的实施例提供的测量标记结构的方法中衍射级次通过衍射光阑后发生干涉示意图；

图6是本发明实施例提供的测量标记结构的方法中步骤s3的详细步骤流程图；

图7是本发明实施例提供的测量标记结构的方法框图；

图8是本发明实施例提供的测量标记系统框图。

具体实施方式

为使本发明的目的、技术方案和优点更加清楚明白，以下结合具体实施例，并参照附图，对本发明进一步详细说明。

本发明实施例一方面提供了一种测量标记结构的方法，参见图1，所述方法包括：

步骤s1，获取平行的相干光束，将所述相干光束入射对准标记后得到衍射光束，该衍射光束通过衍射光阑发生干涉得到干涉信号，通过探测器测量所述干涉信号的实际光强分布。

首先，需要说明的是，本发明采用的测量装置参见图2，本发明的一个实施例提供了一种测量标记结构的散射装置，所述装置包括：依次排布的辐射光源101、准直系统102、孔径光阑103，设置于所述孔径光阑103之后的照明镜组104和分光镜105，分别设置于所述分光镜105两侧的收集镜组106和聚焦镜组108，以及依次设置于所述聚焦镜组108之后的衍射光阑109和阵列探测器110。

其中，辐射光源101，用于产生空间相干的照明光束；准直系统102和孔径光阑103，用于产生均匀且平行的小尺寸相干照明光束；照明镜组104、分光镜105、收集镜组106，用于构成4f光学系统，将空间相干的窄照明光束入射对准标记；标记结构107，用于产生不同衍射级次的衍射光束；收集镜组106和聚焦镜组108，用于构成4f光学系统，收集衍射光束并将其汇聚于衍射光阑109处；衍射光阑109，用于使衍射光束相互重叠，产生干涉信号；阵列探测器110，用于测量干涉信号。

由此，步骤s1中的所述获取平行的相干光束包括：辐射光源101产生的光束依次通过准直系统102和孔径为300-400μm的孔径光阑103后得到所述平行的相干光束。

需要说明的是，本发明实施例以上述测量装置应用于测量标记结构为例进行说明，因此其采用孔径为300-400μm的孔径光阑，但本发明实施例对孔径光阑的孔径不作具体限制，其可以根据实际待测物的尺寸进行适应性调整。另外，文中所述的“小尺寸”是指光束通过孔径为300-400μm的孔径光阑得到的光束或形成的光斑。

标记结构通常为相位型光栅结构，其结构参数如图3所示，其中1为对准标记的周期，2为对准标记的高度，3为对准标记的侧壁角度，4为对准标记的关键尺寸。

本发明实施例中采用小尺寸相干平行光束照射标记，减小对准光学系统波像的影响：

具体地，首先计算各衍射级次在光瞳处的位置：当测量光束入射光栅标记发生衍射时，由光栅方程可知各衍射光束的衍射角为：

其中d为光栅周期，θ为衍射角，m为衍射级次，λ为测量光波长；

由此，各衍射级次在傅里叶面上的位置为：ξ＝ftanθ其中f为物镜的焦距。

在衍射角较小的情况下，可以近似这样各衍射在傅里叶面上的间隔相等为：

其次，计算采用小尺寸平行相干光束时，各衍射级次在光瞳处各衍射级次的光斑大小ω。

为了降低照明镜组104和收集镜组105光学系统波像差的影响，选择小尺寸的测量光束，同时为了保证光栅的衍射效应，要求测量光束至少覆盖光栅标记3个周期。

假设入射光栅标记的光斑尺寸为ε，则傅里叶面上的光斑大小大约为

由于ε≈3d，所以：ω＜δζ

由此，各衍射级的衍射光斑在收集镜组105的傅里叶面不重合，没有干涉信号的产生，如图4所示。其中401～405表示各衍射光斑，406表示各衍射光斑之间的距离，407表示各衍射光斑的大小，408表示整个光瞳。

由于采用小尺寸的测量光斑，这样测量光斑在光瞳处的大小远小于照明镜组104和收集镜组106光瞳大小，所以在本发明中照明镜组104和收集镜组106光学系统波像差的影响远小于使用较大光瞳的傅里叶散射测量方法。

最后，本发明实施例引入衍射光阑使高衍射级次发生干涉，获得含有高衍射级次的测量信号。

各个在空间分离的衍射级通过聚焦镜组108汇聚于衍射光阑109处，经过衍射效应的影响，各衍射光斑重合，发生干涉，采用阵列探测器110探测远程的光强分布，如图5所示。在入射小孔时，各个离散衍射信号可以表示为：

其中为em衍射级在小孔处的复振幅，为衍射级的波矢，为由光栅标记形貌决定的相位，wm为光学系统波像差。由于该测量系统中，光学系统的波像差对测量信号的影响较小，可以将其忽略。

此处假设只有两个衍射级，这两个衍射信号可以表示为：

建立如图5中的坐标系，并令衍射光阑109中心为原点，其中波矢可以分解到x轴和z轴，如下表示：

由于光阑处z＝0，这样这两个平面光波传播到光阑的位置时，复振幅分布为：

然后该复振幅通过光阑可以表示为：

eb(x)＝ea(x)t(x)

其中t(x)为光阑的透射函数，当在远场接收该光波时，远场的复振幅分布为透过光阑复振幅的傅里叶变换，如下式表示：

其中t(kx)为光阑透射函数的傅里叶变换。这样远场的光强分布为：

该式中前两项为直流项，此处只考虑最后一项交叉项，该项包含由标记形貌决定的相位信息。通过阵列探测器110接收的光强分布可以表示为：

其中的卷积可以用系数c表示，其真实物理意义为波矢为k1x和k2x光波的重叠度。

这样阵列探测器110接收的光强可以表示为：

考虑所有衍射级次，根据波的叠加原理，可以计算出阵列探测器110的光强为：

其中，n、m均为对准标记的衍射级次；en、em分别为衍射级级次的复振幅；和为由对准标记结构决定的相位，t(kx)为衍射光阑透射函数t(x)的傅里叶变换，kn、km为衍射级次透过衍射光阑的波矢，由散射测量系统放大倍率以及衍射级次的衍射角决定；kx为阵列探测器上不同位置处波矢的x方向分量，由探测器的位置以及测量光的波矢决定。

步骤s2，建立测量标记结构的电磁波仿真模型，通过所述仿真模型得到对准标记的j个不同结构参数下的仿真光强分布，j≥1。

其中，电磁波仿真模型为严格电磁波仿真模型，该模型的建立可以为现有技术中任何一种可行的方法，本发明实施例对此不作具体限定。例如其可以通过严格耦合波法、有限元法、傅里叶模态法等方法得到。

步骤s3，将实际光强分布分别与j个仿真光强分布进行对比，获取使实际光强分布与仿真光强分布之间差异最小的所述结构参数。

在一种可行的方式中，参见图6，并结合图7中的里的方法流程，步骤s3可以通过下列步骤s301-s304实现：

s301，将实际光强分布与仿真光强分布进行对比，获取使所述评价函数值最小的第一结构参数。

具体地，通过电磁波仿真模型，获得不同对准标记结构αj情况下，阵列探测器的一系列仿真光强分布图其中，ω为散射测量系统中的系统参数，i为空间阵列探测器的像素，αj为第j个对准标记结构。

将实际光强分布分别与j个仿真光强分布进行对比，获取使评价函数值最小的第一结构参数。

所述评价函数通过下式表示：

其中，ii(ω，α)为实际光强分布，α为实际光强分布对应的实际结构参数，为第j个仿真光强分布，αj为第j个仿真光强分布对应的仿真结构参数；ω为散射测量系统中的系统参数，i为空间阵列探测器的像素。

s302，通过非线性优化算法将所述第一结构参数进行优化得到第二结构参数。

非线性优化算法例如差分迭代算法等，将所述第一结构参数进行优化得到第二结构参数：αj+1＝αj+δα。

s303，利用第二结构参数通过电磁波仿真模型，获取优化结构参数后的仿真光强分布。

s304，重复步骤s301-s303，直至所述评价函数收敛，得到使实际光强分布与仿真光强分布之间差异最小的所述结构参数。

本发明另一方面还提供了一种测量标记结构的系统800，所述系统包括上文所述的散射装置801，还包括：实际光强分布获取模块802，用于通过散射装置获取对准标记的实际光强分布；仿真光强分布获取模块803，用于建立测量标记结构的电磁波仿真模型，通过所述仿真模型得到对准标记的j个不同结构参数下的仿真光强分布，j≥1；结构参数获取模块804，用于将实际光强分布分别与j个仿真光强分布进行对比，获取使实际光强分布与仿真光强分布之间差异最小的所述结构参数。

以上所述的具体实施例，对本发明的目的、技术方案和有益效果进行了进一步详细说明，所应理解的是，以上所述仅为本发明的具体实施例而已，并不用于限制本发明，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。