时变地震衰减模型的构建方法与流程

本发明涉及地球物理信号分析领域，特别是涉及一种时变地震衰减模型的构建方法。

背景技术：

地震衰减系数可分为平均衰减系数和层间衰减系数，层间衰减系数也叫瞬时衰减系数。本发明人曾经在国际上首次提出根据反射地震数据估算平均衰减系数的方法（qanalysisonreflectionseismicdata,geophysicalresearchletters,vol:31/2004/本发明人）即“反射地震数据的q分析”。该方法的突破点是采用一个组合变量，即频率和时间的乘积作为单个变量而不是各自独立的频率和时间两个变量，将二维的时-频谱转化成以上述乘积变量作为单个自变量的一维函数。籍助于这个乘积变量，地震功率谱的对数转化成了线性函数，这样即可通过线性拟合方式得到衰减系数。但是，由于实际地震数据低频限波作用导致的低频振幅缺失，以及实际地震数据中含有的数据噪声，上述线性拟合即衰减系数的估算结果直接依赖于对乘积变量初始值和截止值的设置，因此，该方法对实际地震数据噪声具有一定的敏感性。

上述“反射地震数据的q分析”一文中也提出了根据平均衰减系数求取层间地震衰减系数的反演计算方法。但是，由于反演计算所用的核算子是一个三角矩阵，反演求解的过程中会存在误差逐层累积的现象，因此该方法在实际地震数据的应用之中不够稳定。实际地震数据反演所得的层间衰减系数中甚至有负值出现。这些负值衰减系数的存在违背了地层介质的实际可能特性，因而没有任何物理意义。

技术实现要素：

本发明目的在于克服现有技术的上述缺陷，提出一种时变地震衰减模型的构建方法。该方法是针对现有地震数据衰减模型估算方法的缺陷，包括在平均衰减系数估算中的缺陷以及在层间衰减系数估算中的缺陷。

为实现上述目的，本发明时变地震衰减模型的构建方法是依据物理原理而提出的根据wang’s子波变化特征估算层间衰减系数的全新方法，通过约束反演地震衰减模型不同波长系数的方式，构建稳定的时变地震衰减模型。本发明的突出优点之一是依据物理原理而提出的根据wang’s子波变化特征估算衰减系数的全新方法。另一个突出优点是，提出通过约束反演衰减模型不同波长系数的方式，构建稳定的时变地震衰减模型。因此，本发明具有提出估算地震衰减系数全新方法，通过约束反演衰减模型不同波长系数的方式，构建稳定时变地震衰减模型的优点。

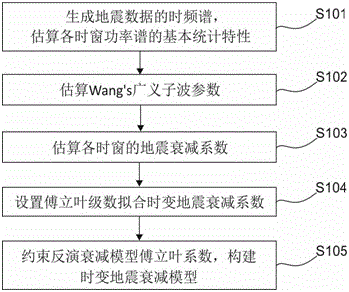
作为优化，实现步骤是：（1）生成地震数据时频谱，估算各时窗的功率谱基本统计特性；（2）估算wang’s广义子波参数；（3）估算各时窗的地震衰减系数；（4）设置傅立叶级数拟合时变地震衰减模型；（5）约束反演衰减模型傅立叶级数的系数，构建时变的地震衰减模型。

作为优化，步骤（1）估算地震数据的时频谱；采用伽柏变换估算地震数据的时频谱，并针对实际地震数据存在的信噪比问题，对时频谱进行加权平均以改善时频谱的信噪比，改善依此得到的地震衰减模型的可靠性；估算各时窗地震数据的功率谱基本统计特性，即均值频率和频率方差。步骤（1）中采用伽柏变换估算地震数据的时频谱时，针对实际地震数据存在的信噪比问题，对地震时频谱进行加权平均改善时频谱的信噪比。本发明提出：提取地震剖面中一组相邻地震道的时频谱，按照其局部倾角对时频谱进行加权平均；对于叠前共中心点道集，沿走时曲线对其时频谱加权平均。通过上述加权平均的方式改善地震时频谱的信噪比，从而改善依此得到的地震衰减模型的可靠性。

步骤（1）估算各时窗的功率谱基本统计特性，即均值频率和频率方差。根据每个时窗的地震数据功率谱估算均值频率fm及其频率方差fσ如下：

式中f是地震信号的频率，w²(f)则是其功率谱。

作为优化，步骤（2）估算wang’s广义子波参数，即固有频率和分数阶值，分为两步优化实现；首先依次估算每个时窗频谱的固有频率和分数阶值；然后对全部固有频率值采用中值滤波获得全局化的子波固有频率，并根据全局化的子波固有频率重新推算每个时窗的子波分数阶值。

步骤（2）估算wang’s广义子波参数，即固有频率和分数阶值，分为两步迭代实现。首先，根据每个时窗的频谱依次估算子波的固有频率f0和分数阶值u：

然后，对全部固有频率值采用中值滤波获得全局化的子波固有频率f0，并根据全局化的子波固有频率重新推算对应于每个时窗的子波分数阶值u：

作为优化，步骤（3）估算各时窗的地震衰减系数，本发明提出根据wang’s子波变化特征估算地震衰减系数的全新表达式如下：

式中α是地震信号的衰减系数，f0是子波的固有频率，τ是地震信号在介质中两点之间的传播时间，(ua,ub)是两时间位置的地震子波分数阶值。

即本发明提出的上述估算衰减系数全新方法依据如下物理基础。地震信号在粘弹性介质中传播：

式中wa(f,0)和wb(f,τ)是两时间位置地震子波的频谱，q是地层介质的品质因子。由上式得到地震信号衰减系数如下：

地震子波wa(f,0)和wb(f,τ)采用wang’s子波定义：

因此地震衰减系数可表达为

设置f=f0，最终得到地震衰减系数估算式如下：

。

作为优化，步骤（3）依据物理原理提出的地震衰减系数全新表达式，

也可近似表示为

因此，估算地震衰减系数的表达式具有以下两个特征：首先，地震衰减系数跟(ua-ub)/τ成近似线性关系；其次，两时间位置的地震子波分数阶值(ua,ub)需要满足下列条件：。但是，分数阶值(ua,ub)因存在估算误差有可能不满足上述条件，本发明提出通过约束反演方式构建时变地震衰减模型。

作为优化，步骤（4）设置傅立叶级数拟合时变地震衰减模型。采用傅立叶级数拟合各时窗的地震衰减系数，构建初始的时变衰减模型α(τ)：

式中∆k是波数增量，{c0,ci,si}是傅立叶级数的系数。本发明采用不同波长及其系数表征时变衰减模型，将时变衰减模型α(τ)转换成2m+1个傅立叶级数的系数，z={c0,ci,si,i=(1,m)}。

作为优化，步骤（5）约束反演衰减模型傅立叶级数的系数，构建时变的地震衰减模型；根据各时窗估算的衰减系数可得到两组平均衰减系数，一组是根据两个子波直接估算得到的平均衰减系数ᾶ(τ)，另一组是根据层间衰减系数用rms计算得到的平均值ᾶrms(τ)；依照上述两组平均衰减系数构建反演问题，通过反演衰减模型不同波长系数的方法，将反演问题转从一个欠定问题转化成超定问题，从而最终获得稳定的时变地震衰减模型。

作为优化，步骤（5）中提出反演衰减模型的傅立叶级数系数的约束反演方法：

式中(ts,te)分别是纳入反演的平均衰减系数最浅时间和最深时间，z0是步骤(4)中给出的层间衰减系数的初始估算模型，用作反演计算的约束条件，μ是其约束系数；根据上述反演结果z最终构建地震衰减模型z→α(τ)。

步骤（5）中时变衰减系数α(τ)是层间衰减系数，也叫瞬时衰减系数。设平均衰减系数为ᾶ(τ)，从起始时间点τa到任意时间点τb>τa，有两组平均衰减系数：一组是根据w(τa)和w(τb)两个子波估算得到的平均衰减系数ᾶ(τ)，另一组是根据[τa,τb]之间的层间衰减系数α(τ)用rms计算得到的平均值ᾶrms(τ)：

如果在上述反演问题中直接反演衰减模型α(τ)，由于需要反演的层间衰减系数总数大于平均衰减系数总数，该反演问题是一个欠定问题。因此，本发明提出反演衰减模型不同波长分量的系数，将反演问题由欠定问题转化成超定问题，从而最终获得稳定的时变衰减模型。

综上所述，本发明具有如下两个突出优点。本发明的一个突出优点是，依据物理原理提出了根据wang’s子波变化特征估算地震衰减系数的全新方法。本发明的另一个突出优点是，通过约束反演地震衰减模型不同波长系数的方式，构建稳定的时变地震衰减模型。

附图说明

图1是时变地震衰减模型的构建方法实现的基本流程图。图2是实施例的地震道集及其对应的均值频率估算结果。

图3是上述地震衰减系数全新表达式的图示，纵轴是地震信号的衰减系数。左图的横轴是地震信号的传播时间τ，右图的横轴是比值(ua-ub)/τ，这里(ua,ub)是地震子波的分数阶值。图中设置地震子波的固有频率为f0=30赫兹，分数阶值，五条曲线分别对应分数阶值=1.8、1.6、1.4、1.2、1.0。图3左图（a）展示对于同样量的子波特征变化(ua-ub)，传播时间越长说明地震衰减系数越小。图3右图（b）展示地震衰减系数跟(ua-ub)/τ成近似线性关系。

图4是根据实际地震数据运用本发明方法构建的时变地震衰减模型，该实施例显示近地表地层的强衰减、时间1.42秒以上碎屑岩层中含煤地层的超强衰减、以及深部碳酸盐岩层中的较弱衰减特征。

具体实施方式

本发明时变地震衰减模型的构建方法是依据物理原理而提出的根据wang’s子波变化特征估算层间衰减系数的全新方法，通过约束反演地震衰减模型不同波长系数的方式，构建稳定的时变地震衰减模型。本发明的突出优点之一是依据物理原理，提出根据wang’s子波变化特征估算地震衰减系数的全新方法。另一个突出优点是，提出通过约束反演衰减模型不同波长系数的方式，构建稳定的时变地震衰减模型。实现步骤是：（1）生成地震数据时频谱，估算各时窗的功率谱基本统计特性；（2）估算wang’s广义子波参数；（3）估算各时窗的地震衰减系数；（4）设置傅立叶级数拟合时变地震衰减模型；（5）约束反演衰减模型傅立叶级数的系数，构建时变的地震衰减模型。本发明具有依据物理原理提出估算地震衰减系数全新方法，通过约束反演衰减模型不同波长系数的方式，构建稳定时变地震衰减模型的优点。

步骤（1）估算地震数据的时频谱；采用伽柏变换估算地震数据的时频谱，并针对实际地震数据存在的信噪比问题，对时频谱进行加权平均以改善时频谱的信噪比，改善依此得到的地震衰减模型的可靠性；估算各时窗地震数据的功率谱基本统计特性，即均值频率和频率方差。步骤（1）中采用伽柏变换估算地震数据的时频谱时，针对实际地震数据存在的信噪比问题，对地震时频谱进行加权平均以改善时频谱的信噪比，从而改善依此得到的地震衰减模型的可靠性。本发明提出：提取地震剖面中一组相邻地震道的时频谱，按照其局部倾角对时频谱进行加权平均；对于叠前共中心点道集，沿走时曲线对其时频谱加权平均。步骤（1）中估算各时窗的功率谱基本统计特性，即均值频率和频率方差。根据每个时窗的地震数据功率谱估算均值频率fm及其频率方差fσ如下：

式中f是地震信号的频率，w²(f)则是其功率谱。

步骤（2）估算wang’s广义子波参数，即固有频率和分数阶值，分为两步迭代实现；首先根据每个时窗的频谱依次估算子波的固有频率和分数阶值；然后对全部固有频率值采用中值滤波获得全局化的子波固有频率，并根据全局化的子波固有频率重新推算对应于每个时窗的子波分数阶值。

步骤（2）估算wang’s广义子波参数，即固有频率和分数阶值，分为两步迭代实现。首先，根据每个时窗的频谱依次估算子波的固有频率f0和分数阶值u：

然后，对全部固有频率值采用中值滤波获取全局化的子波固有频率f0，并根据全局化的子波固有频率重新推算对应于每个时窗的子波分数阶值u：

步骤（3）估算各时窗的地震衰减系数，本发明提出根据wang’s子波变化特征估算地震衰减系数的全新表达式如下：

式中α是地震信号的衰减系数，f0是子波的固有频率，τ是地震信号在介质中两点之间的传播时间，(ua,ub)是两时间位置的地震子波分数阶值。

步骤（3）提出的上述估算衰减系数全新方法依据如下物理原理。地震信号在粘弹性介质中传播：

式中wa(f,0)和wb(f,τ)是两时间位置地震子波的频谱，q是地层介质的品质因子。由上式得到地震信号衰减系数如下：

地震子波wa(f,0)和wb(f,τ)采用wang’s子波定义：

因此地震衰减系数可表达为

设置f=f0，最终得到地震衰减系数估算式如下：

步骤（3）依据物理原理提出的地震衰减系数全新表达式，

也可近似表示为

因此，估算地震衰减系数的表达式具有以下两个特征：首先，地震衰减系数跟(ua-ub)/τ成近似线性关系；其次，两时间位置的地震子波分数阶值(ua,ub)需要满足下列条件：

。但是，分数阶值(ua,ub)因存在估算误差有可能不满足上述条件，本发明提出通过约束反演方式构建时变地震衰减模型。

步骤（4）设置傅立叶级数拟合时变地震衰减模型。采用傅立叶级数拟合各时窗的地震衰减系数，构建初始的时变衰减模型α(τ)：

式中∆k是波数增量，{c0,ci,si}是傅立叶级数的系数。本发明采用不同波长及其系数表征时变衰减模型，将时变衰减模型α(τ)转换成2m+1个傅立叶级数的系数，z={c0,ci,si,i=(1,m)}。

步骤（5）约束反演衰减模型傅立叶级数的系数，构建时变的地震衰减模型；根据各时窗估算的衰减系数可得到两组平均衰减系数，一组是根据两个子波直接估算得到的平均衰减系数ᾶ(τ)，另一组是根据层间衰减系数用rms计算得到的平均值ᾶrms(τ)；依照上述两组平均衰减系数构建反演问题，通过反演衰减模型不同波长系数的方法，将反演问题转从一个欠定问题转化成超定问题，从而最终获得稳定的时变地震衰减模型。

步骤（5）中提出反演衰减模型的傅立叶级数系数的约束反演方法：

式中(ts,te)分别是纳入反演的平均衰减系数最浅时间和最深时间，z0是步骤(4)中给出的层间衰减系数的初始估算模型，用作反演计算的约束条件，μ是其约束系数；根据上述反演结果z最终构建地震衰减模型z→α(τ)。

步骤（5）中时变衰减系数α(τ)是层间衰减系数，也叫瞬时衰减系数。设平均衰减系数为ᾶ(τ)，从起始时间点τa到任意时间点τb>τa，有两组平均衰减系数：一组是根据w(τa)和w(τb)两个子波估算得到的平均衰减系数ᾶ(τ)，另一组是根据[τa,τb]之间的层间衰减系数α(τ)用rms计算得到的平均值ᾶrms(τ)：

如果在上述反演问题中直接反演衰减模型α(τ)，由于需要反演的层间衰减系数总数大于平均衰减系数总数，该反演问题是一个欠定问题。因此，本发明提出反演衰减模型不同波长分量的系数，将反演问题由欠定问题转化成超定问题，从而最终获得稳定的时变衰减模型。

综上所述，本发明具有如下两个突出优点。本发明的一个突出优点是，依据物理基础，提出根据wang’s子波形态变化特征估算地震衰减系数的全新方法。本发明的另一个突出优点是，提出通过优化反演地震衰减模型不同波长系数的方式，构建稳定的时变地震衰减模型。

为使本发明的技术方案和优点更加清楚明白，下面对本发明实施方式作详细具体说明。图1是本发明方法实现的基本流程图。

步骤s101，生成地震数据时频谱，估算各时窗功率谱的基本统计特性。采用伽柏变换估算地震数据的时频谱时，针对实际地震数据存在的信噪比问题，对地震时频谱进行加权平均以改善时频谱的信噪比，从而改善依此得到的地震衰减模型的可靠性。本发明提出：提取地震剖面中一组相邻地震道的时频谱，按照其局部倾角对时频谱进行加权平均；对于叠前共中心点道集，沿走时曲线对其时频谱加权平均。估算各时窗的功率谱基本统计特性，即均值频率fm及其频率方差fσ：

式中f是地震信号的频率，w²(f)则是其功率谱。图2是实施例的地震道集及其对应的均值频率估算结果。

步骤s102，估算wang’s广义子波参数，即固有频率和分数阶值，分为两步迭代实现。首先，根据每个时窗的频谱依次估算子波的固有频率f0和分数阶值u：

然后，对全部固有频率值采用中值滤波获取全局化的子波固有频率f0，并根据全局化的子波固有频率重新推算对应于每个时窗的子波分数阶值u：

步骤s103估算各时窗的地震衰减系数，本发明提出根据wang’s子波变化特征估算地震衰减系数的全新表达式如下：

式中α是地震信号的衰减系数，f0是子波的固有频率，τ是地震信号在介质中两点之间的传播时间，(ua,ub)是两时间位置的地震子波分数阶值。本发明方法所依据的物理原理已经在《发明内容》部分做了详细陈述，在此不再赘述。

图3是上述地震衰减系数全新表达式的图示，纵轴是地震信号的衰减系数。左图的横轴是地震信号的传播时间τ，右图的横轴是比值(ua-ub)/τ，这里(ua,ub)是地震子波的分数阶值。图中设置地震子波的固有频率为f0=30赫兹，分数阶值，五条曲线分别对应分数阶值=1.8、1.6、1.4、1.2、1.0。图3左图（a）展示对于同样量的子波特征变化(ua-ub)，传播时间越长说明地震衰减系数越小。图3右图（b）展示地震衰减系数跟(ua-ub)/τ成近似线性关系。

步骤s103依据物理原理提出的地震衰减系数全新表达式，

也可近似表示为

因此，估算地震衰减系数的表达式具有以下两个特征：首先，正如图3所示，地震衰减系数跟(ua-ub)/τ成近似线性关系；其次，两时间位置的地震子波分数阶值(ua,ub)需要满足下列条件：。但是，分数阶值(ua,ub)因存在估算误差有可能不满足上述条件，本发明提出通过约束反演方式构建时变地震衰减模型。

步骤s104设置傅立叶级数拟合时变地震衰减模型。采用傅立叶级数拟合各时窗的地震衰减系数，构建初始的时变衰减模型α(τ)：

式中∆k是波数增量，{c0,ci,si}是傅立叶级数的系数。本发明采用不同波长及其系数表征时变衰减模型，将时变衰减模型α(τ)转换成2m+1个傅立叶级数的系数，z={c0,ci,si,i=(1,m)}。

步骤s105，约束反演衰减模型的傅立叶系数，构建时变地震衰减模型。上述时变衰减系数α(τ)是层间衰减系数，也叫瞬时衰减系数。设置平均衰减系数为ᾶ(τ)，从起始时间点τa到任意时间点ub>ua，有两组平均衰减系数：一组是根据w(τa)和w(τb)两个子波估算得到的平均衰减系数ᾶ(τ)，另一组是根据[τa,τb]之间的层间衰减系数α(τ)用rms计算得到的平均值ᾶrms(τ)：

依照上述两组平均衰减系数，本发明提出反演衰减模型傅立叶级数系数z的约束反演方法：

式中(ts,te)分别是纳入反演的平均衰减系数最浅时间和最深时间，z0是步骤s104中给出的层间衰减系数的初始估算模型，用作反演计算的约束条件，μ是其约束系数。根据上述反演结果z最终构建地震衰减模型z→α(τ)。图4是根据实际地震数据运用本发明方法构建的时变地震衰减模型，该实施例显示近地表地层的强衰减、时间1.42秒以上碎屑岩层中含煤地层的超强衰减、以及深部碳酸盐岩层中的较弱衰减特征。

如果在上述反演问题中直接反演衰减模型α(τ)，由于需要反演的层间衰减系数总数大于平均衰减系数总数，该反演问题是一个欠定问题。因此，本发明提出反演衰减模型不同波长分量的系数，将反演问题由欠定问题转化成超定问题，从而最终获得稳定的时变衰减模型。

综上所述，本发明的一个突出优点是，依据物理原理提出了根据wang’s子波变化特征估算地震衰减系数的全新方法。本发明的另一个突出优点是，通过约束反演地震衰减模型不同波长系数的方式，构建稳定的时变地震衰减模型。