一种测风雷达探测中流星回波信号的反演方法

1.本发明涉及空间探测技术领域，具体涉及一种测风雷达探测中流星回波信号的反演方法。


背景技术：

2.流星体以11.2-72.8km/s的速度冲进地球大气，在100-300km的高度范围内，稀薄的大气预热了流星体，使其温度在数秒之内快速上升，进而发生熔化和汽化的相态转变，最后烧蚀在70-120km的高度。气化的流星原子与大气分子发生激烈碰撞从而电离，伴随着流星体的飞行形成一条等离子体柱，该等离子体柱通常也被称为流星余迹。流星余迹在形成之后会迅速扩散，研究表明，双极性扩散是扩散过程中最主要的作用，因而，双极性扩散的物理过程很大程度上决定了流星余迹回波信号的性质。
3.不同的流星余迹的双极性扩散会产生不同的电子线密度，根据其各自的电子对回波的散射性质可以将不同的流星余迹分为两类：电子分布较为稀疏，流星余迹的回波信号可以视作其所有电子反射探测波的简单相加，则该流星余迹被定义为欠密的流星余迹；电子分布较为密集，探测波在等离子体电子间的二次散射效应和吸收效应不可忽略从而影响回波性质的，该流星余迹被定义为过密的流星余迹。在主流的风场探测中，一般用到的是欠密的流星余迹回波信号，因此本专利重点模拟欠密流星回波信号的物理模型和回波性质(忽略地磁场影响)。
4.对雷达探测中欠密流星余迹回波信号有效反演,可以较好地模拟欠密流星余迹中电子的运动情况和它对雷达探测波的反射过程，为后续探索和验证与流星事件相关的多普勒频移、接收机间信号的相位差、流星飞行速度、双极性扩散系数等参量提供可靠的物理模型。但是目前尚未有系统全面的对雷达探测中欠密流星余迹回波信号的反演方法。


技术实现要素：

5.本发明的目的是针对现有技术的技术缺陷,提供一种测风雷达探测中流星回波信号的反演方法,以较好地模拟雷达探测中流星余迹的回波信号，为后续探索和验证与流星事件相关的多普勒频移、相位差、流星飞行速度、双极性扩散系数等参量提供了可靠的物理模型。
6.为实现以上技术目的，本发明采用以下技术方案为一种测风雷达探测中流星回波信号的反演方法，其特征在于，包括以下步骤：
7.步骤1：根据输入的初始半径和双极性扩散系数得到随时间变化的所有电子与流星飞行轴线距离的均方根值，根据所有电子与流星飞行轴线距离的均方根值得到流星余迹中随时间和半径变化的电子密度函数；
8.步骤2：截取一定的时间长度，依据流星飞行速度得到该时间内的流星飞行距离；截取一定的流星余迹半径范围，在以流星飞行轴线为中心的半径范围内随机铺满均匀分布的电子微团，根据步骤1中的电子密度函数，计算所有电子微团的电子密度；
9.步骤3：根据电子微团与接收机的距离、探测波频率和脉冲重复时间计算单个电子微团的回波电场强度；对流星余迹中所有电子微团的回波电场强度进行三重积分和相干处理，得到流星余迹中电子群反射雷达探测波的回波相干函数；
10.步骤4：构建相位在[-π,π]均匀分布，振幅服从高斯分布的高斯噪声；构建一定信噪比序列的流星余迹回波复信号；将上述流星余迹回波复信号与高斯噪声依照信噪比序列使用复数加法相叠加，得到不同信噪比的流星余迹模拟信号。
[0011]
作为优选，步骤1所述根据输入的初始半径和双极性扩散系数得到随时间变化的所有电子与流星飞行轴线距离的均方根值，具体为：
[0012][0013]
t∈(0,+∞)
[0014]
其中，t表示时间；r0表示初始半径；d表示双极性扩散系数；r0和d是用户反演时需要输入的值，a表示该均方根值；
[0015]
步骤1所述根据所有电子与流星飞行轴线距离的均方根值得到流星余迹中随时间和半径变化的电子密度函数，具体为：
[0016]
设n(r,t)为该电子密度函数，则
[0017][0018]
r∈(0,+∞)
[0019]
其中，r表示与电子所在位置相对应的流星余迹的半径；
[0020]
作为优选，步骤2所述的截取一定的时间长度为：
[0021]
t∈(0,t]
[0022]
其中，t表示一定的时间长度；
[0023]
步骤2所述的依据流星飞行速度得到的该时间内的流星飞行距离，具体为：
[0024]
设流星飞行速度为vm，且在t∈(0,t]的时间区间内流星做匀速直线飞行运动为：
[0025]
l＝vm*t
[0026]
l∈(0,l]
[0027]
其中，l表示流星飞行的距离区间，l表示研究时段内流星飞行的最大距离；步骤2所述的截取一定的流星余迹半径范围为：
[0028]
r∈(0,λ/2]
[0029]
其中，λ为雷达探测波的波长；
[0030]
步骤2所述的在以流星飞行轴线为中心的半径范围内随机铺满均匀分布的电子微团，具体为：
[0031]
在l∈(0,l]，r∈(0,λ/2]三维空间内，设l所在的直线为z轴，与l垂直的平面内两条垂直的直线分别为x轴和y轴,有：
[0032]
x＝λ*rand(1,n)-λ/2
[0033]
y＝λ*rand(1,n)-λ/2
[0034]
z＝l*rand(1,n)
[0035]
其中，x表示电子微团在三维直角坐标系中x轴的分量；y表示电子微团在三维直角
坐标系中y轴的分量；z表示电子微团在三维直角坐标系中z轴的分量；rand(1,n)表示随机函数，生成n个均匀分布在区间(0,1)的随机数；
[0036]
步骤2所述的根据步骤1中的电子密度函数，计算所有电子微团的电子密度，具体为：
[0037]
设在流星余迹中的第i个电子微团的三维坐标为(xi,yi,zi)，其中，xi表示第i个电子微团在三维直角坐标系中x轴的分量；yi表示第i个电子微团在三维直角坐标系中y轴的分量；zi表示第i个电子微团在三维直角坐标系中z轴的分量；那么，所述第i个电子微团所对应的流星余迹的半径为：
[0038][0039]
i∈(1,n]
[0040]
所述第i个电子微团所对应的时间为：
[0041]
t
mic,i
＝t-zi/vm[0042]
i∈(1,n]
[0043]
所述第i个电子微团所对应的电子密度为：
[0044][0045]
其中，r0表示初始半径；
[0046]
对所有的n个电子微团进行如上计算，即可得到所有电子微团的电子密度；
[0047]
作为优选，步骤3所述的根据电子微团与接收机的距离、探测波频率和回波时间计算单个电子微团的回波相位，具体为：
[0048]
设流星余迹中第i个电子微团与接收机的距离为ri，探测波的频率为ω，探测波的波数为k；脉冲重复时间为t
prf
，设第i个电子微团回波的回波电场强度为e
r,mic,i
，那么有：
[0049]er,mic,i
＝(2z0φ
e,i
)
1/2
*n(r
mic,i
,t
mic,i
)*exp(-j*(ωt
prf-2kri))
[0050]
i∈(1,n]
[0051]
其中，z0为自由空间的波阻抗；φ
e,i
为第i个电子微团散射的辐射在接收天线处的功率通量；n(r
mic,i
,t
mic,i
)表示第i个电子微团所对应的电子密度；
[0052]
步骤3所述的对流星余迹中所有电子微团的回波电场强度进行三重积分和相干处理，得到流星余迹中电子群反射雷达探测波的回波相干函数，具体为：
[0053]
将步骤2中的l∈(0,l]区间向左平移1/4，重新命名为对于时间区间t∈(0,t]内的某一时刻t
′
，流星余迹的长度区间为对该长度区间内所有电子微团的回波电场强度进行三重积分和相干处理，得到流星余迹中电子群反射雷达探测波的回波相干函数er，有：
[0054][0055]
其中，z0表示自由空间的波阻抗；φ
e,i
表示第i个电子微团散射的辐射在接收天线处的功率通量，n(r
mic,i
,t
mic,i
)表示第i个电子微团所对应的电子密度；ω表示探测波的频率；t
prf
表示脉冲重复时间；k表示探测波的波数；ri表示第i个电子微团与接收机的距离；
[0056]
作为优选，步骤4所述的构建相位在[-π,π]均匀分布，振幅服从高斯分布的高斯噪声，具体为：
[0057]
所述振幅服从高斯分布的高斯噪声由高斯噪声的振幅模型、高斯噪声的相位模型、高斯噪声模型构成；
[0058]
构建高斯噪声的振幅模型a
noise
：
[0059]
所述构建高斯噪声的振幅模型a
noise
，具体为：
[0060]anoise
＝μ+σ*randn(1,n
noise
)
[0061]
其中，μ表示a
noise
的均值；σ表示a
noise
的标准差；randn(1,n
noise
)表示生成数量为n
noise
的服从均值为0，标准差为1的正态分布序列；
[0062]
构建高斯噪声的相位模型p
noise
：
[0063]
所述构建高斯噪声的相位模型p
noise
，具体为：
[0064]
p
noise
＝2π*rand(1,n
noise
)-π
[0065]
其中，rand(1,n
noise
)表示随机函数，生成n
noise
个均匀分布在区间(0,1)的随机数；
[0066]
构建高斯噪声模型noise：
[0067]
所述构建高斯噪声模型noise，具体为：
[0068]
将高斯噪声的振幅模型a
noise
和高斯噪声的相位模型p
noise
相结合，生成长度为n
noise
的高斯噪声序列noise，有：
[0069]
noise＝a
noise
*exp(-j*p
noise
)
[0070]
步骤4所述的构建一定信噪比序列的流星余迹回波复信号，具体为：
[0071]
构建信噪比序列snr，有：
[0072]
snr＝snr
min
:snr
interval
:snr
max
[0073]
其中，snr
min
表示信噪比序列snr中的最小值；snr
max
表示信噪比序列snr中的最大值；snr
interval
表示信噪比序列snr中值的间隔；上式表示生成总数为(snr
max-snr
min
)/snr
interval
的信噪比序列snr；
[0074]
设信噪比序列snr中的第k个信噪比为snrk，有
[0075][0076]
k∈(1,(snr
max-snr
min
)/snr
interval
]
[0077]
其中，signalk表示流星余迹回波复信号序列中的第k个回波复信号(与snrk相对应)，表示signalk的振幅最大值，有：
[0078]
signalk＝mk*er[0079]
k∈(1,(snr
max-snr
min
)/snr
interval
]
[0080]
其中，mk是为构建不同信噪比的回波信号而需要回波相干函数er乘以的系数序列的第k个系数；从设定的信噪比序列中解出如同mk的m系数序列，即可构建该信噪比序列对应的流星余迹回波复信号；
[0081]
步骤4所述的将上述流星余迹回波复信号与高斯噪声依照信噪比序列使用复数加法相叠加，通过复数加法得到不同信噪比的流星余迹模拟信号，具体为：
[0082]
设流星余迹回波复信号序列中的第k个回波复信号为signalk，那么它对应的流星余迹模拟信号simu_sk为：
[0083]
simu_sk＝signalk+noise
[0084]
k∈(1,(snr
max-snr
min
)/snr
interval
]
[0085]
其中，simu_sk表示流星余迹模拟信号序列中的第k个流星余迹模拟信号；
[0086]
使用同样方法得到上述所有不同信噪比下的流星余迹模拟信号。
[0087]
与现有技术相比，本发明具有如下优点和有益效果：
[0088]
较好地模拟了欠密流星余迹中电子的运动情况
[0089]
较好地模拟了欠密流星余迹中的电子对雷达探测波的回波信号；
[0090]
反演信号包含了与流星事件相关的多普勒频移、接收机间信号的相位差、流星飞行速度、双极性扩散系数等参量，为后续的探索和验证提供了可靠的物理模型
[0091]
该方法可广泛应用于空间探测和空间物理等相关行业。
附图说明
[0092]
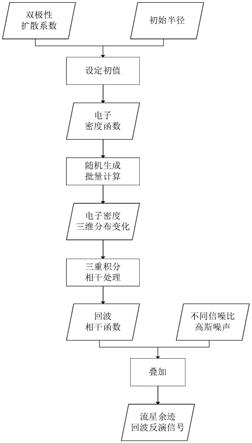
图1：为流星回波信号的反演方法流程图；
[0093]
图2：为电子密度函数随时间和半径的变化示意图；
[0094]
图3：为流星余迹电子相对密度的三维分布示意图；
[0095]
图4：为流星余迹电子相对密度在x轴和z轴所围成平面的剖面图；
[0096]
图5：为回波相干函数的相对振幅；
[0097]
图6：为回波相干函数的相位；
[0098]
图7：为30db信噪比反演复信号与一个真实复信号的对比。
具体实施方式
[0099]
以下将对本发明的具体实施方式进行详细描述。为了避免过多不必要的细节，在以下实施例中对属于公知的结构或功能将不进行详细描述。以下实施例中所使用的近似性语言可用于定量表述，表明在不改变基本功能的情况下可允许数量有一定的变动。除有定义外，以下实施例中所用的技术和科学术语具有与本发明所属领域技术人员普遍理解的相同含义。
[0100]
为了克服现有技术的局限，本发明提出一种测风雷达探测中流星回波信号的反演方法。该方法根据输入的初始半径和双极性扩散系数得到随时间变化的所有电子与流星飞行轴线距离的均方根值，根据所有电子与流星飞行轴线距离的均方根值得到流星余迹中随时间和半径变化的电子密度函数；根据流星飞行速度得到一定的时间长度内的流星飞行距离，截取一定的流星余迹半径范围，在以流星飞行轴线为中心的半径范围内随机铺满均匀分布的电子微团，根据上一步骤中的电子密度函数，计算所有电子微团的电子密度；根据电
子微团与接收机的距离、探测波频率和脉冲重复时间计算单个电子微团的回波电场强度；对流星余迹中所有电子微团的回波电场强度进行三重积分和相干处理，得到流星余迹中电子群反射雷达探测波的回波相干函数；构建相位在[-π,π]均匀分布，振幅服从高斯分布的高斯噪声,构建一定信噪比序列的流星余迹回波复信号,将上述流星余迹回波复信号与高斯噪声依照信噪比序列使用复数加法相叠加，得到不同信噪比的流星余迹模拟信号。本发明较好地模拟了雷达探测中流星余迹的回波信号，为后续探索和验证与流星事件相关的多普勒频移、相位差、流星飞行速度、双极性扩散系数等参量提供了可靠的物理模型。
[0101]
本发明的实施例是对信噪比序列为2db-30db(分辨率0.01db)欠密流星余迹回波信号的反演，反演方法流程图如图1所示，具体步骤如下：
[0102]
步骤1，根据输入的初始半径和双极性扩散系数得到随时间变化的所有电子与流星飞行轴线距离的均方根值，根据所有电子与流星飞行轴线距离的均方根值得到流星余迹中随时间和半径变化的电子密度函数；
[0103]
步骤1所述根据输入的初始半径和双极性扩散系数得到随时间变化的所有电子与流星飞行轴线距离的均方根值，具体为：
[0104][0105]
t∈(0,+∞)
[0106]
其中，t表示时间；r0表示初始半径(此处设为1.53m)；d表示双极性扩散系数(此处设为3.3)；r0和d是用户反演时需要输入的值，a表示该均方根值；
[0107]
步骤1所述根据所有电子与流星飞行轴线距离的均方根值得到流星余迹中随时间和半径变化的电子密度函数，具体为：
[0108]
设n(r,t)为该电子密度函数，则
[0109][0110]
r∈(0,+∞)
[0111]
其中，r表示与电子所在位置相对应的流星余迹的半径；
[0112]
本例中，电子密度函数随时间和半径的变化如图2所示；
[0113]
步骤2，截取一定的时间长度，依据流星飞行速度得到该时间内的流星飞行距离；截取一定的流星余迹半径范围，在以流星飞行轴线为中心的半径范围内随机铺满均匀分布的电子微团，根据步骤1中的电子密度函数，计算所有电子微团的电子密度；
[0114]
步骤2所述的截取一定的时间长度为：
[0115]
t∈(0,t]
[0116]
其中，t表示一定的时间长度(此处设为0.3s)；
[0117]
步骤2所述的依据流星飞行速度得到的该时间内的流星飞行距离，具体为：
[0118]
设流星飞行速度为vm(此处设为20km/s)，且在t∈(0,t]的时间区间内流星做匀速直线飞行运动为：
[0119]
l＝vm*t
[0120]
l∈(0,l]
[0121]
其中，l表示流星飞行的距离区间，l表示研究时段内流星飞行的最大距离(此处为
6km)；
[0122]
步骤2所述的截取一定的流星余迹半径范围为：
[0123]
r∈(0,λ/2]
[0124]
其中，λ为雷达探测波的波长(此处为10m)；
[0125]
步骤2所述的在以流星飞行轴线为中心的半径范围内随机铺满均匀分布的电子微团，具体为：
[0126]
在l∈(0,l]，r∈(0,λ/2]三维空间内，设l所在的直线为z轴，与l垂直的平面内两条垂直的直线分别为x轴和y轴,有：
[0127]
x＝λ*rand(1,n)-λ/2
[0128]
y＝l*rand(1,n)-λ/2
[0129]
z＝l*rand(1,n)
[0130]
其中，x表示电子微团在三维直角坐标系中x轴的分量；y表示电子微团在三维直角坐标系中y轴的分量；z表示电子微团在三维直角坐标系中z轴的分量；rand(1,n)表示随机函数，生成n个(此处设为10000个)均匀分布在区间(0,1)的随机数；
[0131]
步骤2所述的根据步骤1中的电子密度函数，计算所有电子微团的电子密度，具体为：
[0132]
设在流星余迹中的第i个电子微团的三维坐标为(xi,yi,zi)(此处xi＝2,yi＝3,zi＝3)，其中，xi表示第i个电子微团在三维直角坐标系中x轴的分量；yi表示第i个电子微团在三维直角坐标系中y轴的分量；zi表示第i个电子微团在三维直角坐标系中z轴的分量；那么，所述第i个电子微团所对应的流星余迹的半径为：
[0133][0134]
i∈(1,n]
[0135]
所述第i个电子微团所对应的时间为：
[0136]
t
mic,i
＝t-zi/vm[0137]
i∈(1,n]
[0138]
所述第i个电子微团所对应的电子密度为：
[0139][0140]
其中，r0表示初始半径；
[0141]
对所有的n个电子微团进行如上计算，即可得到所有电子微团的电子密度；
[0142]
本例中，流星余迹电子相对密度的三维分布图如图3所示；
[0143]
本例中，流星余迹电子相对密度在x轴和z轴所围成平面的剖面图如图4所示；
[0144]
步骤3，根据电子微团与接收机的距离、探测波频率和脉冲重复时间计算单个电子微团的回波电场强度；对流星余迹中所有电子微团的回波电场强度进行三重积分和相干处理，得到流星余迹中电子群反射雷达探测波的回波相干函数；
[0145]
步骤3所述的根据电子微团与接收机的距离、探测波频率和回波时间计算单个电
子微团的回波相位，具体为：
[0146]
设流星余迹中第i个电子微团与接收机的距离为ri(此处设为150km)，探测波的频率为ω(此处为30mhz)，探测波的波数为k(此处为0.63)；脉冲重复时间为t
prf
(此处设为2ms)，设第i个电子微团回波的回波电场强度为e
r,mic,i
，那么有：
[0147]er,mic,i
＝(2z0φ
e,i
)
1/2
*n(r
mic,i
,t
mic,i
)*exp(-j*(ωt
prf-2kri))
[0148]
i∈(1,n]
[0149]
其中，z0为自由空间的波阻抗(此处为120π)；φ
e,i
为第i个电子微团散射的辐射在接收天线处的功率通量(此处设为3.75
×
10-45
)；n(r
mic,i
,t
mic,i
)表示第i个电子微团所对应的电子密度；
[0150]
步骤3所述的对流星余迹中所有电子微团的回波电场强度进行三重积分和相干处理，得到流星余迹中电子群反射雷达探测波的回波相干函数，具体为：
[0151]
将步骤2中的l∈(0,l]区间向左平移1/4，重新命名为对于时间区间t∈(0,t]内的某一时刻t
′
，流星余迹的长度区间为对该长度区间内所有电子微团的回波电场强度进行三重积分和相干处理，得到流星余迹中电子群反射雷达探测波的回波相干函数er，有：
[0152][0153]
其中，z0表示自由空间的波阻抗(此处为120π)；φe表示三维柱坐标中每个积分微元对应的电子微团的在接收天线处的功率通量，n(r
mic
,t
mic
)表示三维柱坐标中每个积分微元对应的电子微团的电子密度，r表示三维柱坐标中每个积分微元对应的电子微团的与接收机间的距离；φ
e,i
表示第i个电子微团散射的辐射在接收天线处的功率通量(此处设为3.75
×
10-45
)，n(r
mic,i
,t
mic,i
)表示第i个电子微团所对应的电子密度；ω表示探测波的频率(此处为30mhz)；t
prf
表示脉冲重复时间(此处设为2ms)；k表示探测波的波数(此处为0.63)；ri表示第i个电子微团与接收机的距离(此处设为150km)；
[0154]
本例中，回波相干函数的相对振幅如图5所示；
[0155]
本例中，回波相干函数的相位如图6所示；
[0156]
步骤4，构建相位在[-π,π]均匀分布，振幅服从高斯分布的高斯噪声；构建一定信噪比序列的流星余迹回波复信号；将上述流星余迹回波复信号与高斯噪声依照信噪比序列使用复数加法相叠加，得到不同信噪比的流星余迹模拟信号。
[0157]
步骤4所述的构建相位在[-π,π]均匀分布，振幅服从高斯分布的高斯噪声，具体
为：
[0158]
所述振幅服从高斯分布的高斯噪声由高斯噪声的振幅模型、高斯噪声的相位模型、高斯噪声模型构成；
[0159]
构建高斯噪声的振幅模型a
noise
：
[0160]
所述构建高斯噪声的振幅模型a
noise
，具体为：
[0161]anoise
＝μ+σ*randn(1,n
noise
)
[0162]
其中，μ表示a
noise
的均值(此处设为150)；σ表示a
noise
的标准差(此处设为30)；randn(1,n
noise
)表示生成数量为n
noise
的服从均值为0，标准差为1的正态分布序列；
[0163]
构建高斯噪声的相位模型p
noise
：
[0164]
所述构建高斯噪声的相位模型p
noise
，具体为：
[0165]
p
noise
＝2π*rand(1,n
noise
)-π
[0166]
其中，rand(1,n
noise
)表示随机函数，生成n
noise
个均匀分布在区间(0,1)的随机数；
[0167]
构建高斯噪声模型noise：
[0168]
所述构建高斯噪声模型noise，具体为：
[0169]
将高斯噪声的振幅模型a
noise
和高斯噪声的相位模型p
noise
相结合，生成长度为n
noise
的高斯噪声序列noise，有：
[0170]
noise＝a
noise
*exp(-j*p
noise
)
[0171]
步骤4所述的构建一定信噪比序列的流星余迹回波复信号，具体为：
[0172]
构建信噪比序列snr，有：
[0173]
snr＝snr
min
:snr
interval
:snr
max
[0174]
其中，snr
min
表示信噪比序列snr中的最小值(此处设为2db)；snr
max
表示信噪比序列snr中的最大值(此处设为30db)；snr
interval
表示信噪比序列snr中值的间隔(此处设为0.01db)；上式表示生成总数为(snr
max-snr
min
)/snr
interval
(此处为2800)的信噪比序列snr；
[0175]
设信噪比序列snr中的第k个信噪比为snrk，有
[0176][0177]
k∈(1,(snr
max-snr
min
)/snr
interval
]
[0178]
其中，signalk表示流星余迹回波复信号序列中的第k个回波复信号(与snrk相对应)，表示signalk的振幅最大值，有：
[0179]
signalk＝mk*er[0180]
k∈(1,(snr
max-snr
min
)/snr
interval
]
[0181]
其中，mk是为构建不同信噪比的回波信号而需要回波相干函数er乘以的系数序列的第k个系数；从设定的信噪比序列中解出如同mk的m系数序列，即可构建该信噪比序列对应的流星余迹回波复信号；
[0182]
步骤4所述的将上述流星余迹回波复信号与高斯噪声依照信噪比序列使用复数加法相叠加，通过复数加法得到不同信噪比的流星余迹模拟信号，具体为：
[0183]
设流星余迹回波复信号序列中的第k个回波复信号为signalk，那么它对应的流星余迹模拟信号simu_sk为：
[0184]
simu_sk＝signalk+noise
[0185]
k∈(1,(snr
max-snr
min
)/snr
interval
]
[0186]
其中，sumu_sk表示流星余迹模拟信号序列中的第k个流星余迹模拟信号；
[0187]
使用同样方法得到上述所有不同信噪比下的流星余迹模拟信号。
[0188]
本例中，30db信噪比反演复信号与2020年1月1日北纬40
°
xy站点一个真实复信号的对比如图7所示。
[0189]
具体实施时，本发明可采用计算机软件技术实现自动运行流程。
[0190]
以上对本发明的实施例进行了详细说明，但所述内容仅为本发明的较佳实施例，并不用以限制本发明。凡在本发明申请范围内所做的任何修改、等同替换和改进等，均应包含在本发明保护范围之内。