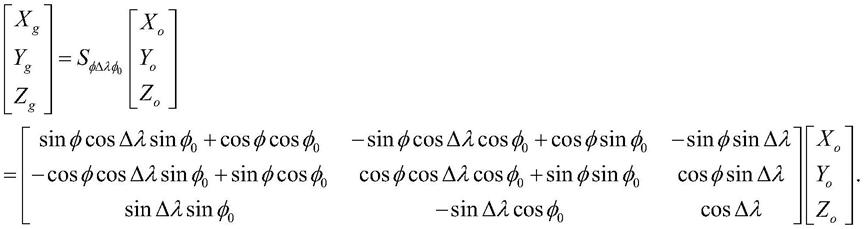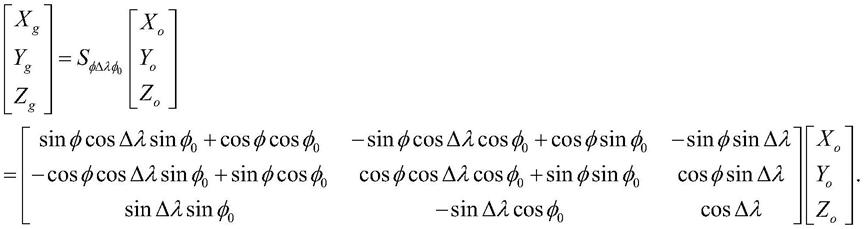
1.本发明涉及捷联惯性导航动态初始对准领域,具体涉及基于车载发射平台的捷联惯性导航系统轨迹发生器设计方法。
背景技术:2.随着无人机应用的迅速发展,以车辆为载体的发射平台解决了无人机应用中迅速转移发射移地点及行驶间发射的问题。对于民用无人机,可广泛应用于大地测量、灾情监视、森林防火、人工降雨、飞播造林等各种工作中,提高无人机发射机动性能。通常在无人机发射前,首先要进行导航信息的初始化,其中获得初始姿态信息的过程即初始对准,车载发射平台的飞行器惯性导航系统初始对准实质上是动基座传递对准过程,初始对准精度的高低将会直接影响到后续惯性导航精度,是进行飞行器研发设计的前提条件。
3.本专利基于这一实际应用的需要,设计车载发射平台捷联惯性导航系统轨迹发生器,为捷联惯导系统的算法设计、精度仿真等前期验证工作提供数据支撑,减少研究中半实物、实物仿真试验,解决硬件支撑缺乏的问题。已有捷联惯性导航系统轨迹发生器设计方法仅能模拟几种典型的运行情况,本专利结合实际车载发射过程,分别建立了发射车、发射架运动模型,最大限度地模拟实际运动。同时,现有轨迹发生器仅针对单一平台,本专利通过调整发射车、发射架相关参数,轨迹发生器可产生相同发射平台不同运动状态及不同发射平台运动数据,设计方法具有普遍适用性。
技术实现要素:4.根据实际运动情况,在准备发射阶段,无人机惯导系统敏感的运动是发射车与发射架运动的叠加。为模拟惯导系统轨迹数据,需要同时将发射车、发射架、惯导运动转换到地心赤道坐标系中进行计算,力学建模过程复杂且难度大。为实现上述发明目的,本发明采用下述的技术方案:
5.一种基于车载发射平台的捷联惯导系统轨迹发生器设计方法,包括如下步骤:
6.s1,坐标系定义,采用车载方式发射的飞行器体积较小,飞行时间较短,因此本发明忽略地球自转的影响,假设地球为椭圆球。具体定义如下坐标系:
7.(1)惯性坐标系s
e-oexeyeze。惯性坐标系固连于地心oe,不随地球自转。其中oe为地球中心,oexe轴位于赤道面内并指向春分点,oeze轴与地球自转轴重合,oeye轴由右手法则确定。
8.(2)地心赤道旋转坐标系s
r-oexryrzr。地心赤道旋转坐标系固连于地心oe,其为动坐标系随着地球自转。oezr垂直于赤道平面,指向北极;xr轴和yr轴在赤道平面内,且xr轴与子午线相交,yr轴由右手法则确定。
9.(3)当地铅垂坐标系s
g-oxgygzg。坐标系原点为飞行器质心o,oyg在地心 oe与质心o的连线上,oxg在过质心o的子午面内垂直于oyg,指向北极为正, ozg轴与其他两轴构成右手直角坐标系,即“北-天-东”原则,该坐标系随地球自转。
10.(4)航空器坐标系s
b-oxbybzb。飞行器质心o为坐标原点,oxb轴在飞行器主对称平面内沿纵轴指向头部,oyb轴也在主对称平面内与oxb轴垂直,当oxb轴与oxgzg平面呈现锐角时,oyb指向天,ozb轴垂直于该对称面;该坐标系为右手直角坐标系;该坐标系随地球自转。
11.(5)车体坐标系s
c-ocxcyczc。车质心oc为坐标原点,ocxc轴在车主对称平面内沿纵轴指向头部,ocyc轴也在主对称平面内与ocxc轴垂直,oczc由右手定则确定;当飞行器平放在发射车上时(航空器朝向车头),s
c-ocxcyczc可以由s
b-oxbybzb平移得到,该坐标系随地球自转。
12.(6)当地固定铅垂坐标系s
o-oox
oyozo
。坐标系原点为仿真初始时刻的飞行器质心oo,o
oyo
在地心oe与质心oo的连线上,ooxo在过质心oo的子午面内垂直于o
oyo
,指向北极为正,o
ozo
轴与其他两轴构成右手直角坐标系,即“北-天-东”原则,该坐标系随地球自转。
13.s2,坐标系转换关系,各坐标系间的转换关系如图2所示,具体转换关系为:
14.(1)当地铅锤坐标系与航空器坐标系,航空器坐标系sb与当地铅锤坐标系 sg的空间关系可以使用以下三个姿态角来定义:俯仰角偏航角ψ1以及滚转角γ1;则这两个坐标系之间的转换矩阵为
[0015][0016]
其中,xbybzb为航空器的坐标;xgygzg为航空器的当地铅垂坐标;t为转置符号。只需将中的姿态角替换为对应的变量。
[0017]
(2)地铅垂坐标系与当地固定铅垂坐标系,当地铅垂坐标系sg与当地固定铅垂坐标系so间的空间转换关系可以使用三个角度来实现:φ,
△
λ,φ0,φ和λ分别为当地铅垂坐标系坐标原点o的纬度和经度,φ0和λ0分别为当地固定铅垂坐标系原点oo的纬度和经度;则
△
λ为o与oo之间精度之差,即
△
λ=λ-λ0;则这两个坐标系之间的转换矩阵为
[0018][0019]
(3)当地铅垂坐标系与地心赤道旋转坐标系,当地铅垂坐标系sg与地心赤道旋转坐标系sr间的空间转换关系可以使用φ,λ两个角度来实现;φ和λ分别为当地铅垂坐标系坐标原点o的纬度和经度;这两个坐标系之间的转换矩阵为
[0020]
[0021]
s3,建立发射车姿态运行动力学方程,假设发射车质心位置不变,j为发射车转动惯量矩阵,发射车为面对称构型,则有j
xz
=j
yz
=0,矩阵可表示为
[0022][0023]
绕发射车三个轴的相对惯性坐标系的转动角速度在车体坐标系三个轴上的投影设定为ω
cg
=[ω
cxg ω
cyg ω
czg
]
t
,
[0024]
则发射车三个轴的转动角速度可以由下式计算得到
[0025][0026]
其中,f
cy
和f
cz
为车体坐标系y和z轴上的合外力;若f
cy
作用在单个轮子上,则 l
cz
为两个前轮间距的一半,l
cx
为同侧前后两个轮间距的一半;若f
cy
作用在两个前轮或两个后轮上,则l
cz
=0,l
cx
为同侧前后两个轮间距的一半;若f
cy
作用在同侧轮上,则f
cy
l
cx
=0,l
cz
为两个前轮间距的一半,l
cx
为同侧前后两个轮间距的一半。
[0027]
设绕发射车三个轴的相对当地固定铅垂坐标系的转动角速度在车体坐标系三个轴上的投影设定为ωc=[ω
cx ω
cy ω
cz
]
t
,其值可由下式计算得到
[0028][0029]
s4,建立飞行器质心姿态运行动力学方程,假设发射车质心位置不变,且飞行器为面对称构型,则i
xz
=i
yz
=0,转动惯量矩阵为
[0030][0031]
绕飞行器三个轴的相对连接点(发射车与飞行器的连接点)的转动角速度设定为ω
bg
′
=[ω
bxg
′ꢀ
ω
byg
′ꢀ
ω
bzg
′
]
t
;已知
[0032][0033]
则可以得到下式
[0034][0035]
其中发射架与发射车连接处的合力矩可以由下式计算得到
[0036][0037]
mf为发射架质量。绕飞行器三个轴的相对惯性坐标系的转动角速度在航空器坐标系三个轴上的投影设定为ω
bg
=[ω
bxg ω
byg ω
bzg
]
t
,其值可以由下式计算得到
[0038][0039]
设绕飞行器三个轴的相对当地固定铅垂坐标系的转动角速度在航空器坐标系三个轴上的投影设定为ωb=[ω
bx ω
by ω
bz
]
t
;其值可由下式计算得到
[0040][0041]
s5,建立飞行器线运动动力学方程,在当地固定铅垂坐标系中建立发射车质心运动学模型
[0042][0043]
其中f
cy
为发射车在车体坐标系y轴上的合力。在当地固定铅垂坐标系中的飞行器质心速度为
[0044][0045]
进而可以计算得到飞行器质心在当地固定铅垂坐标系上的位置为 od=[x
do y
do z
do
]
t
。
[0046]
s6,建立飞行器和发射车相对当地铅垂坐标系的姿态角运动方程,若飞行器质心位置是运动的,则o与oo不重合。由当地铅垂坐标系的定义可知,若坐标原点的经纬度发生变化,则会造成当地铅垂坐标系发生偏转,相应的发射车与飞行器姿态角也会发生变化。
[0047]
其中,r0为oo与oe的矢径,其值可以由下式计算得到
[0048][0049]
其中已知地球长半轴ae=6378140m,地球扁率αe=(a
e-be)/ae=1/298.257,be为地球短半轴长;则飞行器质心到地心之间的距离r可以由下式计算
[0050][0051]
进而由空间转换关系可知地球经纬度可以由下式计算得到
[0052][0053]
由于飞行器质心的经纬度发生变化,导致坐标系的方向发生变化,而这种变化需要叠加到飞行器运动中。若绕飞行器三个轴的相对当地铅垂坐标系的转动角速度在航空器坐标系三个轴上的投影设定为ω
b1
=[ω
bx1 ω
by1 ω
bz1
]
t
;其值可以由下式计算得到
[0054][0055]
则飞行器相对当地铅垂坐标系的三个姿态角速度可以由下式计算得到
[0056][0057]
类似的,若绕发射车三个轴的相对当地铅垂坐标系的转动角速度在车体坐标系三个轴上的投影设定为ω
c1
=[ω
cx1 ω
cy1 ω
cz1
]
t
;其值可以由下式计算得到
[0058][0059]
则发射车相对当地铅垂坐标系的三个姿态角速度可以由下式计算得到
[0060][0061]
(1)本发明解决了一类车载发射平台动力学建模问题,通过参数调整,可提供多型号发射车及发射架运行模型,解决了这一领域轨迹发生器缺失问题。
[0062]
(2)本发明提出的车载发射平台动力学模型同时考虑了发射车运动与发射架运动,与传统单一平台单一动力学模型相比,建模过程复杂,实现难度大,本专利首次解决了这一问题;
[0063]
(3)本发明提出的轨迹发生器设计方法基于六自由度动力学模型生成仿真数据,设计了发射架运动控制器,更加符合实际情况,大大提高了仿真轨迹数据的真实性。
[0064]
(4)本专利考虑到平台及惯导系统误差的影响,采用的设计方法具有可扩展性,用户可能根据实际情况加入到不同坐标系模型中计算仿真数据。
附图说明
[0065]
图1为坐标系定义示意图;
[0066]
图2为坐标系间的转换关系;
[0067]
图3为航空器观测到的俯仰角;
[0068]
图4为航空器观测到的偏航角;
[0069]
图5为航空器观测到的滚转角;
[0070]
图6为航空器观测到的经度;
[0071]
图7为航空器观测到的纬度;
[0072]
图8为航空器观测到的高度。
具体实施方式
[0073]
下面结合附图和具体实施例对本发明的技术内容进行详细具体的说明。
[0074]
如图1与图2所示,本发明提供的一种基于车载发射平台的捷联惯导系统轨迹发生器设计方法,包括坐标系的定义与转换。下面对这一过程做详细具体的说明。
[0075]
s1,坐标系定义,采用车载方式发射的飞行器体积较小,飞行时间较短,因此本专利忽略地球自转的影响,假设地球为椭圆球。具体定义如下坐标系:
[0076]
(1)惯性坐标系s
e-oexeyeze。惯性坐标系固连于地心oe,不随地球自转。其中oe为地球中心,oexe轴位于赤道面内并指向春分点,oeze轴与地球自转轴重合,oeye轴由右手法则确定。
[0077]
(2)地心赤道旋转坐标系s
r-oexryrzr。地心赤道旋转坐标系固连于地心oe,其为动坐标系随着地球自转。oezr垂直于赤道平面,指向北极;xr轴和yr轴在赤道平面内,且xr轴与子午线相交,yr轴由右手法则确定。
[0078]
(3)当地铅垂坐标系s
g-oxgygzg。坐标系原点为飞行器质心o,oyg在地心 oe与质心o的连线上,oxg在过质心o的子午面内垂直于oyg,指向北极为正, ozg轴与其他两轴构成右手直角坐标系,即“北-天-东”原则,该坐标系随地球自转。
[0079]
(4)航空器坐标系s
b-oxbybzb。飞行器质心o为坐标原点,oxb轴在飞行器主对称平面内沿纵轴指向头部,oyb轴也在主对称平面内与oxb轴垂直,当oxb轴与oxgzg平面呈现锐角时,oyb指向天,ozb轴垂直于该对称面;该坐标系为右手直角坐标系;该坐标系随地球自转。
[0080]
(5)车体坐标系s
c-ocxcyczc。车质心oc为坐标原点,ocxc轴在车主对称平面内沿纵轴指向头部,ocyc轴也在主对称平面内与ocxc轴垂直,oczc由右手定则确定;当飞行器平放在发射车上时(航空器朝向车头),s
c-ocxcyczc可以由 s
b-oxbybzb平移得到,该坐标系随地球自转。
[0081]
(6)当地固定铅垂坐标系s
o-oox
oyozo
。坐标系原点为仿真初始时刻的飞行器质心oo,o
oyo
在地心oe与质心oo的连线上,ooxo在过质心oo的子午面内垂直于o
oyo
,指向北极为正,o
ozo
轴与其他两轴构成右手直角坐标系,即“北-天-东”原则,该坐标系随地球自转。
[0082]
s2,坐标系转换关系,各坐标系间的转换关系如图2所示,具体转换关系为:
[0083]
(1)当地铅锤坐标系与航空器坐标系,航空器坐标系sb与当地铅锤坐标系 sg的空间关系可以使用以下三个姿态角来定义:俯仰角偏航角ψ1以及滚转角γ1;则这两个坐标系之间的转换矩阵为
[0084][0085]
其中,只需将中的姿态角替换为对应的变量。
[0086]
(2)地铅垂坐标系与当地固定铅垂坐标系,当地铅垂坐标系sg与当地固定铅垂坐标系so间的空间转换关系可以使用三个角度来实现:φ,
△
λ,φ0,φ和λ分别为当地铅垂坐标系坐标原点o的纬度和经度,φ0和λ0分别为当地固定铅垂坐标系原点oo的纬度和经度;则
△
λ为o与oo之间精度之差,即
△
λ=λ-λ0;则这两个坐标系之间的转换矩阵为
[0087][0088]
(3)当地铅垂坐标系与地心赤道旋转坐标系,当地铅垂坐标系sg与地心赤道旋转坐标系sr间的空间转换关系可以使用两个角度来实现:φ,λ,φ和λ分别为当地铅垂坐标系坐标原点o的纬度和经度;这两个坐标系之间的转换矩阵为
[0089][0090]
s3,建立发射车姿态运行动力学方程,假设发射车质心位置不变,且发射车为面对称构型,则j
xz
=j
yz
=0,转动惯量矩阵为
[0091][0092]
绕发射车三个轴的相对惯性坐标系的转动角速度在车体坐标系三个轴上的投影设定为ω
cg
=[ω
cxg ω
cyg ω
czg
]
t
;已知
[0093][0094]
则发射车三个轴的转动角速度可以由下式计算得到
[0095][0096]
其中,f
cy
和f
cz
为车体坐标系y和z轴上的合外力;若f
cy
作用在单个轮子上,则 l
cz
为两个前轮间距的一半,l
cx
为同侧前后两个轮间距的一半;若f
cy
作用在两个前轮或两个后轮上,则l
cz
=0,l
cx
为同侧前后两个轮间距的一半;若f
cy
作用在同侧轮上,则f
cy
l
cx
=0,l
cz
为两个前轮间距的一半,l
cx
为同侧前后两个轮间距的一半。
[0097]
设绕发射车三个轴的相对当地固定铅垂坐标系的转动角速度在车体坐标系三个轴上的投影设定为ωc=[ω
cx ω
cy ω
cz
]
t
,其值可由下式计算得到
[0098][0099]
s4,建立飞行器质心姿态运行动力学方程,假设发射车质心位置不变,且飞行器为面对称构型,则i
xz
=i
yz
=0,转动惯量矩阵为
[0100][0101]
绕飞行器三个轴的相对连接点(发射车与飞行器的连接点)的转动角速度设定为ω
bg
′
=[ω
bxg
′ꢀ
ω
byg
′ꢀ
ω
bzg
′
]
t
;已知
[0102][0103]
则可以得到下式
[0104][0105]
其中发射架与发射车连接处的合力矩可以由下式计算得到
[0106][0107]
mf为发射架质量。绕飞行器三个轴的相对惯性坐标系的转动角速度在航空器坐标系三个轴上的投影设定为ω
bg
=[ω
bxg ω
byg ω
bzg
]
t
,其值可以由下式计算得到
[0108][0109]
设绕飞行器三个轴的相对当地固定铅垂坐标系的转动角速度在航空器坐标系三个轴上的投影设定为ωb=[ω
bx ω
by ω
bz
]
t
;其值可由下式计算得到
[0110][0111]
s5,建立飞行器线运动动力学方程,在当地固定铅垂坐标系中建立发射车质心运动学模型
[0112][0113]
其中f
cy
为发射车在车体坐标系y轴上的合力。在当地固定铅垂坐标系中的飞行器质心速度为
[0114][0115]
进而可以计算得到飞行器质心在当地固定铅垂坐标系上的位置为 od=[x
do y
do z
do
]
t
。
[0116]
s6,建立飞行器和发射车相对当地铅垂坐标系的姿态角运动方程,若飞行器质心位置是运动的,则o与oo不重合。由当地铅垂坐标系的定义可知,若坐标原点的经纬度发生变化,则会造成当地铅垂坐标系发生偏转,相应的发射车与飞行器姿态角也会发生变化。
[0117]
其中,r0为oo与oe的矢径,其值可以由下式计算得到
[0118][0119]
其中已知地球长半轴ae=6378140m,地球扁率ae=(a
e-be)/ae=1/298.257,be为地球短半轴长;则飞行器质心到地心之间的距离r可以由下式计算
[0120][0121]
进而由空间转换关系可知地球经纬度可以由下式计算得到
[0122][0123]
由于飞行器质心的经纬度发生变化,导致坐标系的方向发生变化,而这种变化需要叠加到飞行器运动中。若绕飞行器三个轴的相对当地铅垂坐标系的转动角速度在航空器坐标系三个轴上的投影设定为ω
b1
=[ω
bx1 ω
by1 ω
bz1
]
t
;其值可以由下式计算得到
[0124][0125]
则飞行器相对当地铅垂坐标系的三个姿态角速度可以由下式计算得到
[0126][0127]
类似的,若绕发射车三个轴的相对当地铅垂坐标系的转动角速度在车体坐标系三个轴上的投影设定为ω
c1
=[ω
cx1 ω
cy1 ω
cz1
]
t
;其值可以由下式计算得到
[0128][0129]
则发射车相对当地铅垂坐标系的三个姿态角速度可以由下式计算得到
[0130][0131]
这里设定发射车转动惯量矩阵为
[0132][0133]
航空器转动惯量矩阵为
[0134][0135]
航空器质心初始经纬度为λ=111度,φ=40.8度。发射车头朝北,且水平停置,航空器在发射车上平放;且lc=7m,l
cx
=7m和l
cy
=1m。
[0136]
若驱动航空器的转动力矩大小不受限制,这里设计如下控制器
[0137][0138]
设定当时,进行其它机动,这里设定转动目标为
[0139]
ψ
1f
=40
°
;γ
1f
=0
°
。
[0140]
设定发射车驱动发射架的转动角速度为10
°
/s,得到子惯导系统的仿真结果如图3-8所示。