弱超声导波信号的双混沌系统检测方法

1.本发明属于超声导波无损检测方法领域，特别是一种弱超声导波信号的双混沌系统检测方法。


背景技术：

2.导波因其具有传播距离长、可同时检测管道表面和内部缺陷等优点，被认为在检测埋地管道、含包裹层管道中具有独特的优势，然而对于小缺陷或远距离缺陷检测，测试得到的缺陷回波往往十分微弱，甚至完全淹没在噪声信号中。
3.为了克服这一困难，研究人员利用混沌系统敏感性增强小缺陷来进行检测。然而，利用混沌检测系统进行的信号识别只能判定待检信号中是否含有缺陷回波，而无法判定缺陷回波的出现时刻和大小，成为本领域内难以克服的困难，致使混沌检测方法在超声导波信号检测中的应用十分有限。
4.中国发明申请cn103323529a，本发明公开了一种利用改进型杜芬混沌系统识别斜裂纹管道超声导波的方法，有以下步骤：1)在管道的一侧端面激发超声导波信号，使超声导波遍历管道的所有位置；2)在激发端附近的接收端接收超声导波回波信号并记录超声导波管道中传播的时间历程曲线，其中超声导波回波信号包含端面回波信号、噪声信号和淹没在噪声中的斜裂纹缺陷信号；3)利用改进型杜芬混沌系统对超声导波回波信号进行检测与分析，提取并识别淹没在噪声中的斜裂纹缺陷信息，获得整个管道的斜裂纹缺陷情况。该方法虽然可以检测到弱的缺陷回波信号，却无法对信号的幅值和发生时刻进行定位，也就无法实现缺陷的定量分析。
5.中国发明申请cn 105954358b，本发明公开了一种tr与duffing系统相结合的超声导波小缺陷定位检测方法，步骤如下：1)在管道的一端面激发超声导波信号，使超声导波遍历管道的所有位置；2)在激发端附近的另一端面接收超声导波回波信号并记录超声导波管道中传播的时间历程曲线；3)利用改进型杜芬混沌系统对超声导波回波信号进行检测与分析，提取并识别淹没在噪声中的小缺陷信息；4)将得到的带有小缺陷信息的信号进行时间反转后再进行二次激发；5)接收反转信号。该方法中混沌检测系统是一项辅助手段，用以判定检测信号中是否含有缺陷信号，以决定是否有进行时间反转检测的必要。
6.因此，为同时实现缺陷回波信号的检测、定量和定位技术，寻求一种弱超声导波信号的双混沌系统检测方法，来解决该领域中无法对缺陷信号进行定量分析的难题是十分迫切且必要的。


技术实现要素：

7.本发明针对上述现有技术中的缺陷，提出一种弱超声导波信号的双混沌系统检测方法。该方法包括确定目标信号，构造第一混沌系统并确定第一混沌系统阈值，构建第一混沌检测系统并识别目标信号幅值，确定考虑相位影响时的第一混沌系统阈值减小量，构造第二混沌系统并构建第二混沌检测系统，进行目标信号的检测和定位，进行管道缺陷定量
检测以确定管道缺陷的位置和大小。本发明利用双混沌检测系统，通过相位差补偿快速、准确地检测出缺陷回波目标信号的发生时刻，节省了求解资源，提高了分析效率，同时对小缺陷或远距离的检测提供了方向。
8.本发明提供一种弱超声导波信号的双混沌系统检测方法，其包括以下步骤：
9.s1、确定目标信号：设目标信号为调制的单频信号s(t)；
10.s2、构造第一混沌系统并确定第一混沌系统阈值f
c1
；
11.s21、以duffing方程构造第一混沌系统：
[0012][0013]
其中，ω表示第一外驱动力圆频率；c表示第一阻尼且为常数；x表示混沌系统的位移变量；f表示外驱动力幅值；t表示混沌系统的演化时间；
[0014]
s22、在第一参数条件下，变换外驱动力幅值f，得到由周期态向混沌态转变的第一混沌系统阈值f
c1
，将参数为第一混沌系统阈值f
c1
、第一阻尼c、第一外驱动力圆频率ω确定的系统设定为第一混沌系统；
[0015]
s3、构建第一混沌检测系统并识别目标信号幅值：将目标信号叠加到式(2)右侧的外驱动力项上构建第一混沌检测系统，叠加目标信号部分，实现目标信号幅值的识别；
[0016]
s4、确定考虑相位影响时第一混沌系统的阈值减小量；
[0017]
s41、设步骤s1中目标信号与步骤s2中式(2)右侧外驱动力存在相位差当时，步骤s3中第一混沌检测系统变为：
[0018][0019]
其中，ω1表示目标信号圆频率，且ω1＝2πf，f表示目标信号频率；n表示目标信号波谷数；k为整数；a表示目标信号幅值；δt表示目标信号长度，且δt＝2πn/ω；
[0020]
s42、考虑相位影响时，第一混沌系统的阈值减小量δf变为：
[0021][0022]
当时，第一混沌系统的阈值减小量δf取得最大值，为目标信号幅值a；
[0023]
s5、构造第二混沌系统并构建第二混沌检测系统，与第一混沌检测系统联合进行目标信号定位；
[0024]
s51、所述第一混沌系统的外驱动力添加一个初相位进行相位补偿，式(7)变为：
[0025][0026]
s52、变换初相位叠加目标信号，若系统进入混沌态后，减小驱动力幅值，使系统再次回到周期态，记驱动力幅值减小量为第一混沌系统的阈值减小量δf，若系统仍保持
为周期态，记δf＝0，并绘制曲线，当时，第一混沌系统的阈值减小量δf取得极大值，有(δf)
max
＝a，记此时初相位为
[0027]
s53、构造第二混沌系统：在第二参数条件下，变换外驱动力幅值f，得到该系统由周期态向混沌态转变的第二混沌系统阈值f
c2
；将参数为第二混沌系统阈值f
c2
、第二阻尼c2、第二外驱动力圆频率ω2确定的系统设定为第二混沌系统；
[0028]
s54、构建第二混沌检测系统的数学模型：
[0029][0030]
其中，表示第二混沌检测系统的第二外驱动力补偿初相位；
[0031]
s55、变换第二混沌检测系统的第二外驱动力初相位叠加目标信号，若系统进入混沌态后，减小驱动力幅值，使系统再次回到周期态，记驱动力幅值减小量为第二混沌系统的阈值减小量δf，若系统仍保持为周期态，记δf＝0，并绘制曲线，标记第二混沌系统的阈值减小量δf取得极大值时为
[0032]
s56、目标信号的波峰发生时刻t
x
为：
[0033][0034]
其中，t表示待检信号长度；
[0035]
叠加待检信号的起始时间t0，获得目标信号的真实波峰发生时刻td为：
[0036][0037]
完成目标信号的检测和定位。
[0038]
进一步，所述步骤s3具体包括以下步骤：
[0039]
s31、将目标信号叠加到duffing方程右侧的外驱动力上，则第一混沌检测系统为：
[0040][0041]
s32、考察叠加目标信号部分，有：
[0042][0043]
s33、式(4)中n不超过20，满足限定条件，此时后两项可忽略不计，有：
[0044][0045]
s34、当duffing方程处于周期向混沌转变的临界态时，叠加导波信号，系统变为混沌状态，通过减小式(5)中f
c1
的值，使其再次进入周期，则第一混沌系统的阈值减小量δf：
[0046]
δf＝a
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(6)；
[0047]
利用式(6)实现目标信号幅值的识别。
[0048]
可优选的，所述步骤s1中所述目标信号s(t)满足函数关系：
[0049][0050]
可优选的，所述步骤s2中所述第一参数条件为第一混沌系统的第一阻尼c＝c1，且第一混沌系统的第一外驱动力圆频率ω与目标信号圆频率ω1一致，即ω＝ω1。
[0051]
可优选的，所述步骤s53中所述第二参数条件为第二混沌系统的第二阻尼与第一混沌系统的第一阻尼相同，即c2＝c＝c1，且第二混沌系统的第二外驱动力圆频率ω2满足关系：
[0052]
(ω
1-ω2)t＝π
ꢀꢀꢀꢀꢀ
(10)。
[0053]
可优选的，所述步骤s33中所述限定条件为当待检信号频率与duffing方程驱动力频率相差3％以上时，待检信号将不会引起duffing方程解的改变。
[0054]
可优选的，所述步骤s41中与目标信号发生时刻有关，所述步骤s51和s54通过双混沌检测系统驱动力相位补偿，进行目标信号发生时刻检测。
[0055]
在本发明的一个优选实施方式中，本发明的方法能够应用在管道缺陷的定量检测上。其还包括以下步骤：
[0056]
s6、进行管道缺陷定量检测：基于超声导波的传播速度和结构中垂直入射超声导波的反射定律，确定管道缺陷的位置和大小；
[0057]
s61、当已知超声导波的传播速度为c时，通过步骤s5中求得目标信号的真实波峰发生时刻td，即缺陷回波发生时刻，计算缺陷到信号激励即接收位置的距离l
x
：
[0058][0059]
s62、根据结构中垂直入射超声导波的反射定律，获得反射系数r为：
[0060][0061]
其中，β表示结构截面损失率；
[0062]
s63、反射系数r为缺陷回波幅值ad＝a与入射波幅值a0之比：
[0063][0064]
其中，k表示衰减修正系数，0《k《1；
[0065]
s64、由式(15)和式(16)获得结构截面损失率β：
[0066]
[0067]
s65、基于结构截面损失率β和缺陷到信号激励即接收位置的距离l
x
，确定管道缺陷的位置和大小。
[0068]
与现有技术相比，本发明的技术效果为：
[0069]
1、本发明提出的弱超声导波信号的双混沌系统检测方法，以处于由周期向混沌态转变的duffing方程临界状态作为混沌检测系统，将目标信号叠加到驱动力项上，系统转变为混沌态，再通过调整驱动力幅值，使系统返回周期态，通过驱动力幅值调整量确定了目标信号幅值；实现了利用混沌系统检测弱信号幅值，为目标信号大小评估提供了依据。
[0070]
2、本发明提出的弱超声导波信号的双混沌系统检测方法，构造两个驱动力频率不同、但满足一定关系的duffing混沌系统，对双混沌系统构造驱动力项进行初相位补偿，同时进行弱信号检测，分别绘制两个系统的曲线，通过两条曲线峰值所对应的相位差确定目标信号的发生时刻，以此来确定缺陷位置；利用双混沌检测系统，通过相位差快速、准确地检测出目标信号的发生时刻，节省了求解资源，提高了分析效率，并且所提出的利用曲线进行信号幅值和发生时刻分析，具有直观、快捷的优点。
[0071]
3、本发明提出的弱超声导波信号的双混沌系统检测方法，在管道缺陷定量检测上，由于小缺陷导致了微弱的缺陷回波，同时超声导波信号又经过了较长距离的传播，致使缺陷回波十分微弱，该方法仍然可以准确识别并明显优于传统方法，提高了管道超声导波检测小缺陷或远距离的检测效率，对于提高超声导波检测效率具有重要意义。
附图说明
[0072]
通过阅读参照以下附图所作的对非限制性实施例所作的详细描述，本技术的其它特征、目的和优点将会变得更明显。
[0073]
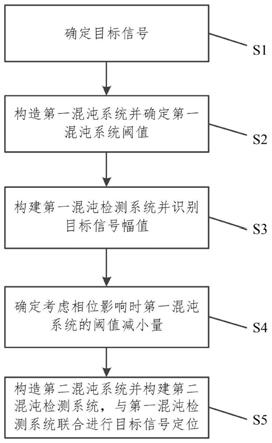
图1是本发明的弱超声导波信号的双混沌系统检测方法流程图；
[0074]
图2是本发明的待识别的目标信号图；
[0075]
图3是本发明的管道超声导波检测缺陷原理图；
[0076]
图4a是本发明的一个具体实施例的实验设备组成图；
[0077]
图4b是本发明的一个具体实施例的实验原理图；
[0078]
图5a是本发明的一个具体实施例的完好管道超声导波测试信号图；
[0079]
图5b是本发明的一个具体实施例的损伤管道超声导波测试信号图；
[0080]
图6a是本发明的采用butterworth带通滤波器滤波后的完好管道信号效果图；
[0081]
图6b是本发明的采用butterworth带通滤波器滤波后的损伤管道信号效果图；
[0082]
图7a是本发明的完好管道第一混沌检测系统识别结果图；
[0083]
图7b是本发明的完好管道第二混沌检测系统识别结果图；
[0084]
图8a是本发明的损伤管道第一混沌检测系统识别结果图；
[0085]
图8b是本发明的损伤管道第二混沌检测系统识别结果图。
具体实施方式
[0086]
下面结合附图和实施例对本技术作进一步的详细说明。可以理解的是，此处所描述的具体实施例仅仅用于解释相关发明，而非对该发明的限定。另外还需要说明的是，为了
便于描述，附图中仅示出了与有关发明相关的部分。
[0087]
需要说明的是，在不冲突的情况下，本技术中的实施例及实施例中的特征可以相互组合。下面将参考附图并结合实施例来详细说明本技术。
[0088]
图1示出了本发明的弱超声导波信号的双混沌系统检测方法，该方法包括以下步骤：
[0089]
s1、确定目标信号：设目标信号为经hanning窗调制的单频信号s(t)，满足函数关系：
[0090][0091]
其中，ω1表示目标信号圆频率，且ω1＝2πf，f表示目标信号频率；n表示目标信号波谷数；a表示目标信号幅值；δt表示目标信号长度，且δt＝2πn/ω。
[0092]
在一个具体实施例中，选频率为f＝70khz，为了与混沌系统求解匹配，进行如下单位变换，70khz＝0.07(1/μs)，ω1＝2π
·
0.07rad/μs≈0.439823rad/μs。取一个完整波包长度为142μs，a＝0.1mv，n＝10，δt≈142(μs)，待识别的目标信号形状如图2所示。
[0093]
s2、构造第一混沌系统并确定第一混沌系统阈值f
c1
。
[0094]
s21、以duffing方程构造第一混沌系统：
[0095][0096]
其中，ω表示第一外驱动力圆频率；c表示第一阻尼且为常数；x表示混沌系统的位移变量；f表示外驱动力幅值；t表示混沌系统演化时间。
[0097]
s22、在第一参数条件下，变换外驱动力幅值f，得到该系统由周期态向混沌态转变的第一混沌系统阈值f
c1
，将参数为第一混沌系统阈值f
c1
、第一阻尼c、第一外驱动力圆频率ω确定的系统设定为第一混沌系统；第一参数条件为第一混沌系统的第一阻尼c＝c1，且第一混沌系统的第一外驱动力圆频率ω与目标信号圆频率ω1一致，即ω＝ω1。
[0098]
在一个具体实施例中，取第一阻尼c＝0.4，得到该系统由周期态向混沌态转变的临界值为f
c1
＝0.45781，将参数为f
c1
＝0.45781，c＝0.4，ω＝ω1确定的系统设定为第一混沌系统。
[0099]
s3、构建第一混沌检测系统并识别目标信号幅值：将目标信号叠加到式(2)右侧的外驱动力上构建第一混沌检测系统，叠加目标信号部分，实现目标信号幅值的识别。
[0100]
s31、将目标信号叠加到duffing方程右侧的外驱动力上，则第一混沌检测系统为：
[0101][0102]
s32、考察叠加目标信号部分，有：
[0103][0104]
s33、式(4)中n不超过20，满足限定条件：当待检信号频率与duffing方程驱动力频
率相差3％以上时，待检信号将不会引起duffing方程解的改变。此时，后两项可忽略不计，有：
[0105][0106]
s34、当duffing方程处于周期向混沌转变的临界态时，叠加导波信号，系统变为混沌状态，通过减小式(5)中f
c1
的值，使其再次进入周期，则第一混沌系统的阈值减小量δf：
[0107]
δf＝a
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(6)；
[0108]
利用式(6)实现目标信号幅值的识别。
[0109]
s4、确定考虑相位影响时第一混沌系统的阈值减小量。
[0110]
s41、设步骤s1中目标信号与步骤s2中式(2)右侧外驱动力项存在相位差当时，步骤s3中第一混沌检测系统变为：
[0111][0112]
其中，k为整数；与目标信号发生时刻有关。
[0113]
s42、考虑相位影响时，第一混沌系统的阈值减小量δf变为：
[0114][0115]
当时，第一混沌系统的阈值减小量δf取得最大值，为目标信号幅值a。
[0116]
s5、构造第二混沌系统并构建第二混沌检测系统，与第一混沌检测系统联合进行目标信号定位。
[0117]
s51、所述第一混沌系统的外驱动力添加一个初相位进行相位补偿，式(7)变为：
[0118][0119]
s52、变换初相位叠加目标信号，若系统进入混沌态后，减小驱动力幅值，使系统再次回到周期态，记驱动力幅值减小量为第一混沌系统的阈值减小量δf，若系统仍保持为周期态，记δf＝0，并绘制曲线，当时，第一混沌系统的阈值减小量δf取得极大值，有(δf)
max
＝a，记此时初相位为
[0120]
s53、构造第二混沌系统：在第二参数条件下，变换外驱动力幅值f，得到该系统由周期态向混沌态转变的第二混沌系统阈值f
c2
；将参数为第二混沌系统阈值f
c2
、第二阻尼c2、第二外驱动力圆频率ω2确定的系统设定为第二混沌系统；所述步骤s53中所述第二参数条件为第二混沌系统的第二阻尼与第一混沌系统的第一阻尼相同，即c2＝c＝c1，且第二混沌系统的第二外驱动力圆频率ω2满足关系：
[0121]
(ω
1-ω2)t＝π
ꢀꢀꢀꢀꢀ
(10)
[0122]
其中，t表示待检信号长度。
[0123]
在一个具体实施例中，第二阻尼c2＝0.4，得到该系统由周期态向混沌态转变的临界值为f
c2
＝0.45609，将参数为f
c2
＝0.45609，c2＝0.4，确定的系统设定为第二混沌系统。
[0124]
s54、构建第二混沌检测系统的数学模型：
[0125][0126]
其中，表示第二混沌检测系统的第二外驱动力补偿初相位。
[0127]
s55、变换第二混沌检测系统的第二外驱动力初相位叠加目标信号，若系统进入混沌态后，减小驱动力幅值，使系统再次回到周期态，记驱动力幅值减小量为第二混沌系统的阈值减小量δf，若系统仍保持为周期态，记δf＝0，并绘制曲线，标记第二混沌系统的阈值减小量δf取得极大值时为
[0128]
s56、目标信号的波峰发生时刻t
x
为：
[0129][0130]
叠加待检信号的起始时间t0，获得目标信号的真实波峰发生时刻td为：
[0131][0132]
完成目标信号的检测和定位。
[0133]
s6、进行管道缺陷定量检测：基于超声导波的传播速度和结构中垂直入射超声导波的反射定律，确定管道缺陷的位置和大小，管道超声导波检测缺陷原理图如图3所示。
[0134]
s61、当已知超声导波的传播速度为c时，通过步骤s5中求得目标信号的真实波峰发生时刻td，即缺陷回波发生时刻，计算缺陷到信号激励即接收位置的距离l
x
：
[0135][0136]
由于缺陷回波的反射系数与缺陷大小成正比，当利用第一混沌检测系统识别出缺陷回波幅值后，可用于求解反射系数，从而得到缺陷大小。
[0137]
s62、根据结构中垂直入射超声导波的反射定律，获得反射系数r为：
[0138][0139]
其中，β表示结构截面损失率。
[0140]
s63、反射系数r为缺陷回波幅值ad＝a与入射波幅值a0之比：
[0141][0142]
其中，k表示衰减修正系数，0《k《1。
[0143]
s64、由式(15)和式(16)获得结构截面损失率β：
[0144][0145]
s65、基于结构截面损失率β和缺陷到信号激励即接收位置的距离l
x
，确定管道缺陷的位置和大小。
[0146]
为了验证本方法的有效性，对一长5m的无缝钢管进行了实验研究，所用设备如图4a所示，主要包括：任意信号发生器、低频放大器和示波器，采用压电换能器激发和采集超声导波信号。测试系统搭建如图4b所示，并采用n＝10，中心频率为70khz的hanning窗调制信号作为激励信号。
[0147]
设置表1所示的3种工况，工况1为完好管道，然后在距激励端3m处利用切割机加工裂纹模拟缺陷，分别令截面减少3.2％和6.4％，为工况2和工况3。
[0148][0149]
表1
[0150]
图5a和5b分别给出了完好管道与截面损失3.2％时的测试信号，可以看出，损失管道测试信号与完好管道相比，也不能清晰的看出缺陷回波。图5a和5b中左侧为入射波ω1，右侧为端面回波ω2，中间部分为待检信号cs。
[0151]
在传统的检测方法中，可以通过滤波的方式，降低噪声影响，从而获得缺陷回波信息。本方法将图4中的测试信号使用butterworth带通滤波器进行滤波，其中心频率为70khz，低频截止频率为60khz，高频截止频率为80khz。滤波后的完好管道与截面损失3.2％的效果分别如图6a和6b所示。图6a和6b图例中上方线型为原始信号a，下方为滤波信号b。
[0152]
显然，滤波后损伤工况依然难以观察到缺陷回波，这主要在于小缺陷导致了微弱的缺陷回波，同时超声导波信号又经过了较长距离的传播，致使缺陷回波十分微弱。
[0153]
采用本发明的双混沌检测系统可以有效的识别出小缺陷回波信息：
[0154]
截取完好管道工况入射波与端面回波中间(0.65ms～1.65ms)的信号为待测信号时(见图5a)，有t＝1ms，，由于其中不含有缺陷回波，只有噪声信号，利用双混沌检测系统识别该信号，第一混沌检测系统和第二混沌检测系统结果分别如图7a和7b所示，可见无论是
第一混沌检测系统还是第二混沌检测系统，δf的值都非常小，且呈随机分布，说明该待检信号中没有缺陷回波(目标信号)。
[0155]
同样，截取损伤工况(0.65ms～1.65ms)之间的信号(见图5b)，并利用双混沌检测系统进行识别，第一混沌检测系统和第二混沌检测系统结果分别如图8a和8b所示，从中可清晰的看出曲线上的峰值。注意到每个混沌检测系统有多个峰值，这与识别结果与相位之间存在周期性相关，利用式(12)，只要保证与满足关系
[0156][0157]
即可。可见，只要在两个混沌检测系统中都选择第一个峰值就可以满足要求。
[0158]
根据图8a的峰值，识别出缺陷回波峰值为0.04mv，依据式(17)识别缺陷大小为截面损失3.45％，相对误差7.81％。
[0159]
利用图8a和8b进行缺陷定位，波速可利用入射波和端面回波的时间差，以及它们的传播距离求得，
[0160]
截取信号起始时刻为：t0＝0.65ms。
[0161]
缺陷回波发生时刻为：
[0162]
缺陷定位为：相对误差为5.63％。
[0163]
采用相同的方法，识别另一个工况，缺陷大小识别结果为截面损失6.61％，相对误差3.28％，缺陷位置识别结果为3.203m，相对误差6.7％，识别精度可满足需求。
[0164]
本发明设计的一种弱超声导波信号的双混沌系统检测方法，以处于由周期向混沌态转变的duffing方程临界状态作为混沌检测系统，将目标信号叠加到驱动力项上，系统转变为混沌态，再通过调整驱动力幅值，使系统返回周期态，通过驱动力幅值调整量确定了目标信号幅值；实现了利用混沌系统检测弱信号幅值，为目标信号大小评估提供了依据；构造两个驱动力频率不同、但满足一定关系的duffing混沌系统，对双混沌系统构造驱动力项的初相位，同时进行弱信号检测，分别绘制两个系统的曲线，通过两条曲线峰值所对应的相位差确定目标信号的发生时刻，以此来确定缺陷位置；利用双混沌检测系统，通过相位差快速、准确地检测出目标信号的发生时刻，节省了求解资源，提高了分析效率，并且所提出的利用曲线进行信号幅值和发生时刻分析，具有直观、快捷的优点；在管道缺陷定量检测上，由于小缺陷导致了微弱的缺陷回波，同时超声导波信号又经过了较长距离的传播，致使缺陷回波十分微弱，该方法仍然可以准确识别并明显优于传统方法，提高了管道超声导波检测小缺陷或远距离的检测效率，对于提高超声导波检测效率具有重要意义。
[0165]
最后所应说明的是：以上实施例仅以说明而非限制本发明的技术方案，尽管参照上述实施例对本发明进行了详细说明，本领域的普通技术人员应当理解：依然可以对本发明进行修改或者等同替换，而不脱离本发明的精神和范围的任何修改或局部替换，其均应涵盖在本发明的权利要求范围当中。