一种基于经验模态分解的光纤光栅光谱信号调制系统的制作方法

1.本发明属于光纤光栅技术领域，特别涉及一种基于经验模态分解的光纤光栅光谱信号调制系统。


背景技术：

2.光纤光栅是利用曝光(或光刻)技术在光纤上形成折射率(或物理损伤)周期性分布结构，能够把光纤中特定波长的光反射，由于其反射波长满足布拉格衍射方程，所以把这种光栅称为光纤布拉格光栅，其作用的实质是在纤芯内形成一个窄带的滤波器，当有光入射到光纤布拉格光栅，处于光纤光栅谐振波长(频率)的光将被反射回去，其它波长(频率)的光会透射过去。光纤光栅受温度、应变、振动等因素的影响，会导致其光纤光栅谐振波长发生变化，这使得光纤光栅可作为传感器。
3.光纤光栅类传感器因探头不需要单独供电、信号可长距离传输等优点，在深海、边远山区、深井等恶劣环境中具有极好的应用前景，适用于地球物理、海洋探测等领域，然而现有较为成熟的光纤光栅类传感器一般采用高斯拟合算法、质心法、自相关法进行解调，精度较低，主要受限于光纤光栅的光谱噪声，光纤光栅光谱噪声包括激光强度噪声、激光频率噪声、散弹噪声和环境中的随机扰动。
4.针对光纤光栅光谱噪声限制光纤光栅类传感器精度的问题，目前尚未提出有效的解决方案。


技术实现要素：

5.本发明克服了现有技术的不足之一，提供了一种基于经验模态分解的光纤光栅光谱信号调制系统，能够解决光谱噪声限制光纤光栅类传感器精度的技术问题，提高光纤光栅类传感器的精度。
6.根据本公开的一方面，本公开提出了一种基于经验模态分解的光纤光栅光谱信号调制系统，所述系统包括：光谱采集模块、模态分解模块、目标滤波器、加法器和光谱寻峰模块；
7.其中，所述光谱采集模块，用于采集光纤光栅光谱信号；
8.所述模态分解模块，用于利用经验模态分解算法将所述光纤光栅光谱信号分解为多个本征模函数；
9.所述目标滤波器，用于对所述本征模函数的噪声进行滤波；
10.所述加法器，用于重构经过滤波后的本征模函数为去噪后的光纤光栅光谱信号；
11.所述光谱寻峰模块，用于利用高斯拟合法对去噪后的光纤光栅光谱信号进行寻峰，得到所述光纤光栅光谱信号调制结果。
12.在一种可能的实现方式中，所述经验模态分解算法为：
[0013][0014]
其中，t为时间，x(t)为光纤光栅光谱信号，ci(t)为本征函数，r(t)为残余量。
[0015]
在一种可能的实现方式中，所述本征模函数具有时域对称性。
[0016]
在一种可能的实现方式中，所述本征模函数包括所述光纤光栅光谱信号的峰值、局部极值点和过零点。
[0017]
在一种可能的实现方式中，在整个时间周期内，多个本征模函数的局部极值点和过零点的数量相同。
[0018]
在一种可能的实现方式中，所述本征函数的局部均值为零。
[0019]
在一种可能的实现方式中，所述目标滤波器为savitzky-golay平滑滤波器。
[0020]
在一种可能的实现方式中，所述去噪后的光纤光栅光谱信号
[0021][0022]
其中，sg[]为savitzky-golay平滑滤波函数，n为数据点的数量，i、k均为正整数。
[0023]
本公开的基于经验模态分解的光纤光栅光谱信号调制系统，包括：光谱采集模块、模态分解模块、目标滤波器、加法器和光谱寻峰模块；光谱采集模块，用于采集光纤光栅光谱信号；模态分解模块，用于利用经验模态分解算法将光纤光栅光谱信号分解为多个本征模函数；目标滤波器，用于对本征模函数的噪声进行滤波；加法器，用于重构经过滤波后的本征模函数为去噪后的光纤光栅光谱信号；光谱寻峰模块，用于利用高斯拟合法对去噪后的光纤光栅光谱信号进行寻峰，得到光纤光栅光谱信号调制结果。能够解决光谱噪声限制光纤光栅类传感器精度的技术问题，提高光纤光栅类传感器的精度。
附图说明
[0024]
附图用来提供对本技术的技术方案或现有技术的进一步理解，并且构成说明书的一部分。其中，表达本技术实施例的附图与本技术的实施例一起用于解释本技术的技术方案，但并不构成对本技术技术方案的限制。
[0025]
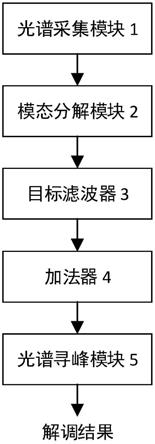
图1示出了根据本公开一实施例的基于经验模态分解的光纤光栅光谱信号调制系统框图。
具体实施方式
[0026]
以下将结合附图及实施例来详细说明本发明的实施方式，借此对本发明如何应用技术手段来解决技术问题，并达到相应技术效果的实现过程能充分理解并据以实施。本技术实施例以及实施例中的各个特征，在不相冲突前提下可以相互结合，所形成的技术方案均在本发明的保护范围之内。
[0027]
另外，附图的流程图示出的步骤可以在诸如一组计算机可执行指令的计算机中执行。并且，虽然在流程图中示出了逻辑顺序，但是在某些情况下，可以以不同于此处的顺序执行所示出或描述的步骤。
[0028]
图1示出了根据本公开一实施例的基于经验模态分解的光纤光栅光谱信号调制系统框图。如图1所示，该调制系统可以包括：光谱采集模块1、模态分解模块2、目标滤波器3、加法器4和光谱寻峰模块5。光谱采集模块1的输出端与模态分解模块2的输入端相连，模态分解模块2的输出端与目标滤波器3的输入端相连，目标滤波器3的输出端与加法器4的输入端相连，加法器4的输出端与光谱寻峰模块5的输入端相连。
[0029]
其中，光谱采集模块1，用于采集光纤光栅光谱信号。
[0030]
模态分解模块2，用于利用经验模态分解算法将光纤光栅光谱信号分解为多个本征模函数。
[0031]
其中，经验模态分解算法为：
[0032]
其中，t为时间，x(t)为光纤光栅光谱信号，ci(t)为本征函数，r(t)为残余量。
[0033]
本征模函数包括光纤光栅光谱信号的峰值、局部极值点和过零点。本征模函数具有时域对称性，在整个时间周期内，多个本征模函数的局部极值点和过零点的数量相同。
[0034]
例如，模态分解模块2利用式(1)对光纤光栅光谱信号进行上述经验模态分级后，可以得到一系列从高频到低频、带宽不等的本征模函数。本征函数具有时域对称性，则多个本征模函数在整个时间范围内，局部极值点和过零点的数目相等，或最多相差一个任意时刻点，且其局部最大值的包络线(上包络线)和局部最小值的包络线(下包络线)平均为0。
[0035]
目标滤波器3，用于对所述本征模函数的噪声进行滤波。目标滤波器为平滑滤波器，例如可以为savitzky-golay平滑滤波器，在此不做限定。
[0036]
savitzky-golay滤波器是一种在时域内基于多项式，通过移动窗口利用最小二乘法进行最佳拟合的方法。是一种直接处理来自时间域内数据平滑问题的方法，与现有滤波器先在频域中定义特性后再转换到时间域不同，能保留光纤光栅光谱信号的相对极大值、极小值和宽度等分布特征。
[0037]
savitzky-golay滤波器可由下式表达：
[0038][0039]
式中，n为数据点的数量，m为sg滤波器的窗口宽度，j为坐标数据中原始数据表中的运行索引。
[0040]
法器4，用于重构经过滤波后的本征模函数为去噪后的光纤光栅光谱信号。
[0041]
例如，用savitzky-golay滤波器对得到多个本征模函数ci(t)进行滤波,将得到的本征模函数在加法器中进行相加，得到重构了的噪声处理后的光纤光栅光谱可以表示为：
[0042][0043]
其中，sg[]为savitzky-golay平滑滤波函数，n为数据点的数量，i、k均为正整数。
[0044]
相对于光纤光栅光谱信号可表示为x(t)，重构了的噪声处理后的光纤光栅光谱y(t)的光谱噪声都得到的有效抑制。
[0045]
寻峰模块5，用于利用高斯拟合法对去噪后的光纤光栅光谱信号进行寻峰，得到光纤光栅光谱信号调制结果。
[0046]
其中，高斯拟合法是将采集获得到的fbg反射谱数据，通过高斯函数进行拟合处理。
[0047]
设拟合高斯函数表达式：
[0048]
[0049]
式中，i0为反射谱强度i的幅值，λc为反射谱中心波长，δλ为反射谱的3db带宽。对上式两边取对数，可得
[0050][0051]
令lni(λ)＝z，可得：
[0052][0053]
可以简写为：
[0054]
z＝xb
ꢀꢀꢀ
式(7)
[0055]
通过最小二乘原理判定最佳拟合曲线：
[0056]
b＝(x
t
x)-1
x
tzꢀꢀꢀ
式(8)
[0057]
求得b0、b1、b2，就可以求出i0、λc、δλ，进而得到光纤光栅光谱信号调制结果i0。
[0058]
本公开的基于经验模态分解的光纤光栅光谱信号调制系统，包括：光谱采集模块、模态分解模块、目标滤波器、加法器和光谱寻峰模块；光谱采集模块，用于采集光纤光栅光谱信号；模态分解模块，用于利用经验模态分解算法将光纤光栅光谱信号分解为多个本征模函数；目标滤波器，用于对本征模函数的噪声进行滤波；加法器，用于重构经过滤波后的本征模函数为去噪后的光纤光栅光谱信号；光谱寻峰模块，用于利用高斯拟合法对去噪后的光纤光栅光谱信号进行寻峰，得到光纤光栅光谱信号调制结果。通过经验模态分解和savitzky-golay滤波器平滑滤波，实现对光纤光栅光谱信号进行分解和降噪，从而降低光谱噪声能够解决光谱噪声限制光纤光栅类传感器精度的技术问题，提高光纤光栅类传感器的精度。
[0059]
虽然本发明所揭露的实施方式如上，但所述的内容只是为了便于理解本发明而采用的实施方式，并非用以限定本发明。任何本发明所属技术领域内的技术人员，在不脱离本发明所揭露的精神和范围的前提下，可以在实施的形式上及细节上作任何的修改与变化，但本发明的专利保护范围，仍须以所附的权利要求书所界定的范围为准。