一种基于反正切函数的变步长谐波电流检测方法与流程

1.本发明属于电力系统的谐波电流检测技术领域，更具体地，涉及一种基于反正切函数的变步长谐波电流检测方法。


背景技术：

2.近年来，大量的电力电子器件在电力系统中的应用使得电力电网谐波污染问题日益突出，严重影响着电网质量和用户设备的安全运行。因而有效治理谐波，对提高电能质量十分重要。其中，最典型的治理方案之一是有源电力滤波器(active power filter，apf)。该apf基于对电网谐波的实时检测，而相应给电网注入一个反相的谐波电流，从而实现对电网的谐波污染补偿、抑制。其性能的好坏很大程度上取决于对谐波电流实时、精确的检测，因此谐波电流检测方法至关重要。在实验中，一般采用假设电源电压us(t)无畸变为标准的正弦电压即us(t)＝umsin(wt)，其中，um为电压幅值，角频率w＝2pf＝100p，则流过非线性负载的周期性非正弦电流为i
l
(t)，其离散值i
l
(k)为：
[0003][0004]
式(1)中：i
l
(k)为负载电流i
l
(t)的采样点，ts为采样周期，k为采样点，ik和ψk分别为第n次谐波的幅值和相位，i
1p
(k)、i
1q
(k)和ih(k)分别为基波有功电流、基波无功电流和谐波电流，ir(k)＝i
1q
(k)+ih(k)为广义谐波电流。
[0005]
随着自适应滤波器的发展，将其应用于谐波电流检测并取得了很好的效果。其中，最小均方算法(least mean square，lms)由于计算简便、收敛性好、偏差性小和稳定性强等特点，因此，其是稳定性最好，应用最广泛的算法之一。但是lms算法的各项指标都受其步长的影响，导致在固定步长的情况下，不能同时保障收敛速度和稳态误差。因此引入变步长方法，在前期利用较大步长使其收敛性加快收敛，在后期利用小步长来减小稳态误差。在自适应谐波电流检测的应用中，现有的性能较好的方法有基于s函数的广义谐波电流检测算法：参考文献1“一种改进变步长的自适应谐波检测算法”(杨建宁，陈婕，关佳军，李自成，电力系统保护与控制[j].2011，39(16)：40-44，52)该方法采用当前误差和前一时刻误差的自相关时间均值估计来消除谐波干扰，再将均值估计通过改进的s函数来控制步长更新。称作基于s函数的广义谐波电流检测算法，该方法不能消除基波无功电流对步长更新的干扰致使稳态误差较大且计算成本高。
[0006]
目前为止，有多位学者提出了一些基于lms的变步长检测法，但都存在着一些问题。有些没有消除同频率谐波对步长的影响，有的计算步骤繁琐，而有的难以运用到实际应用当中。换言之，为了提高自适应谐波检测系统的算法性能，需要设计一种可以提高收敛速度和跟踪性能且降低稳态误差的算法。


技术实现要素：

[0007]
针对现有技术的以上缺陷或改进需求，本发明提出了一种基于反正切函数的变步长谐波电流检测方法，采用该方法进行谐波电流检测，能获得更快的收敛速度和跟踪性能以及更低的稳态误差。
[0008]
本发明提供了一种基于反正切函数的变步长谐波电流检测方法，包括：
[0009]
s1：对周期性非正弦负载电流i
l
(t)采样得到当前k时刻的负载电流离散值i
l
(k)，对i
l
(t)的基波有功电流的参考信号x(t)采样得到当前k时刻的参考信号离散值x(k)，k为时间t的离散点；
[0010]
s2：将参考信号离散值x(k)作为基于反正切函数的自适应滤波器的输入，得到基波有功电流i
1p
(k)的估计值
[0011]
s3：将采样的当前k时刻的负载电流离散值i
l
(k)减去基波有功电流i
1p
(k)的估计值得到误差信号
[0012]
s4：计算自适应滤波器步长的指数值，通过指数函数计算出自适应滤波器下一时刻k+1的步长λ(k+1)；
[0013]
s5：根据误差信号得到当前k时刻去谐波干扰的误差信号，然后，更新得到自适应滤波器的下一时刻k+1的权系数w(k+1)；
[0014]
s6：更新k为下一时刻值，重复执行步骤s1～s5，实时输出周期性非正弦负载电流i
l
(t)的广义谐波电流的估计值
[0015]
在一些可选的实施方案中，由得到当前k时刻的广义谐波电流ir(k)＝i
1q
(k)+ih(k)的估计值表示误差信号e(k)，ih(k)分为高次谐波电流。
[0016]
在一些可选的实施方案中，步骤s4包括：
[0017]
s4.1：由λ
exp
(k-1)＝exp(-λ(k-1))λ(k-1)计算出k-1时刻的控制反正切函数形状的控制因子；
[0018]
s4.2：由λ(k)＝ρ1λ(k-1)+ρ2λ
exp
(k-1)通过前一时刻的指数函数λ
exp
(k-1)计算出自适应滤波器当前k时刻的步长λ(k)，其中，exp(
·
)表示指数运算，ρ1和ρ2为参数。
[0019]
在一些可选的实施方案中，步骤s5包括：
[0020]
s5.1：根据当前k时刻的误差信号e(k)，由反正切运算得到当前k时刻去谐波干扰的误差信号
[0021]
s5.2：由当前k时刻去谐波干扰的误差信号及当前k时刻的自适应滤波器步长更新得到自适应滤波器的下一时刻k+1的权系数w(k+1)。
[0022]
在一些可选的实施方案中，由得到当前k时刻去谐波干扰的误差信号其中，arctan(
·
)表示反正切函数，的初始值设为零。
[0023]
在一些可选的实施方案中，由更新得到自适应滤波器的下一时刻k+1的权系数w(k+1)，其中，λ(k)是当前k时刻的自适应滤波器步长，w(k-1)是k-1时刻自适应滤波器的权系数，w(k)是当前k时刻自适应滤波器的权
系数。
[0024]
在一些可选的实施方案中，ρ1的取值可以为(0.99951)；参数ρ2的取值可以为(00.0001)。
[0025]
总体而言，通过本发明所构思的以上技术方案与现有技术相比，能够取得下列有益效果：
[0026]
本发明采用基于反正切的变步长方法，该方法检测结果精度高、跟踪性能更强。初始时刻检测算法具有较大的步长，可以快速检测到谐波电流。当算法收敛到稳态阶段时，基波有功电流与其估计值基本相等，此时检测算法具有较小步长，可以得出较小的稳态误差。总之，本发明提出的检测方法既可以平衡加快收敛速度和降低稳态误差之间的矛盾，又能够显著抑制非周期畸变电流干扰，提高谐波电流检测效果。
附图说明
[0027]
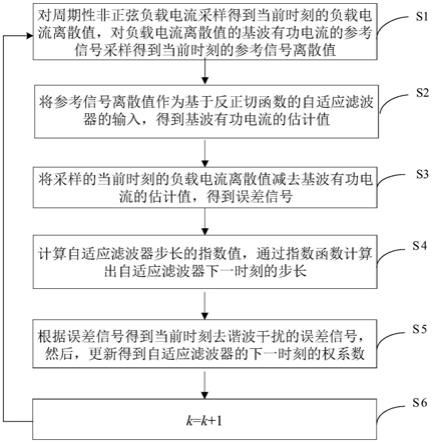
图1是本发明实施例提供的一种基于反正切函数的变步长谐波电流检测方法的流程图；
[0028]
图2是本发明实施例提供的一种针对幅值为
±
1a的负载电流i
l
(t)的工频方波的广义谐波电流曲线；
[0029]
图3是本发明实施例提供的一种针对幅值为
±
1a的负载电流i
l
(t)的工频方波的本发明和基于s函数的广义谐波电流检测值与其理论值的误差曲线。
具体实施方式
[0030]
为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。此外，下面所描述的本发明各个实施方式中所涉及到的技术特征只要彼此之间未构成冲突就可以相互组合。
[0031]
如图1所示是本发明实施例提供的一种基于反正切函数的变步长谐波电流检测方法的流程图，包括以下步骤：
[0032]
s1：采样
[0033]
对周期性非正弦负载电流i
l
(t)采样得到当前k时刻负载电流的离散值i
l
(k)；同时，对i
l
(t)的基波有功电流的参考信号x(t)＝sin(2πft)采样得到当前k时刻的参考信号离散值x(k)，其中频率f＝50hz，k为时间t的离散点；
[0034]
s2：将步骤s1中的参考信号离散值x(k)输入基于反正切函数的自适应滤波器后输出得到基波有功电流i
1p
(k)的估计值即其中，w(k)是当前k时刻自适应滤波器的权系数，若k为初始时刻，则其值取零；
[0035]
s3：用s1步骤中采样的当前k时刻的负载电流离散值i
l
(k)减去基波有功电流i
1p
(k)的估计值得到当前k时刻的广义谐波电流ir(k)＝i
1q
(k)+ih(k)的估计值也是误差信号e(k)，即：
[0036][0037]
其中，i
1q
(k),ih(k)分别是基波无功电流和高次谐波电流；
[0038]
s4：步长λ的更新
[0039]
s4.1：首先，计算出k-1时刻的控制反正切函数形状的控制因子，即：
[0040]
λ
exp
(k-1)＝exp(-λ(k-1))λ(k-1)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)
[0041]
s4.2：然后，通过前一时刻的指数函数λ
exp
(k-1)计算出自适应滤波器当前k时刻的步长λ(k)为：
[0042]
λ(k)＝ρ1λ(k-1)+ρ2λ
exp
(k-1)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0043]
其中，exp(
·
)表示指数运算，参数ρ1的取值可以为(0.99951)；参数ρ2的取值可以为(00.0001)；
[0044]
s5：权系数的更新
[0045]
s5.1：根据s3步骤中当前k时刻的误差信号e(k)，得到当前k时刻去谐波干扰的误差信号
[0046][0047]
其中arctan(
·
)表示反正切函数；的初始值设为零，即
[0048]
s5.2：然后，更新得到自适应滤波器的下一时刻k+1的权系数w(k+1)，即：
[0049][0050]
其中，λ(k)是当前k时刻的自适应滤波器步长，w(k-1)是k-1时刻自适应滤波器的权系数；
[0051]
s6：令k＝k+1，重复步骤s1～步骤s5，即可实时输出周期性非正弦负载电流i
l
(t)的广义谐波电流的估计值
[0052]
仿真实验
[0053]
为了验证本发明的有效性，进行了仿真实验，并与背景技术中提供的现有的文献1的方法进行了对比。
[0054]
仿真实验的参考信号为工频正弦信号，采样频率为10khz。负载电流为1a的工频方波电流，文献1与本发明的参数值设置，如表1所示
[0055]
表1 各方法的实验最优参数取值
[0056]
文献1β＝0.99；γ＝0.99；η＝0.002本发明ρ1＝0.985；ρ2＝0.001
[0057]
图2和图3是在表1参数条件下的本发明与文献1两种方法的谐波电流检测仿真结果：图2为广义谐波电流估计值曲线；图3为广义谐波电流检测值与其理论值的误差曲线。
[0058]
从仿真结果图可以看出：本发明的谐波电流检测的动态响应大约在1周期，而文献1的动态响应时间为1.5周期；文献1和本发明的广义谐波电流检测最小稳态误差分别为
±
0.0125a～
±
0.0296a和
±
0.00125a～
±
0.00296a。所以本发明谐波检测算法具有明显优势。
[0059]
需要指出，根据实施的需要，可将本技术中描述的各个步骤/部件拆分为更多步骤/部件，也可将两个或多个步骤/部件或者步骤/部件的部分操作组合成新的步骤/部件，以实现本发明的目的。
[0060]
本领域的技术人员容易理解，以上所述仅为本发明的较佳实施例而已，并不用以
限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。