一种用于智能轮椅的神经网络PID滑模控制系统的制作方法

本发明涉及智能轮椅的控制领域，特别涉及智能轮椅的神经网络pid滑模控制方法。

背景技术：

中国已经成为世界上老年人口最多的国家，也是人口老龄化发展速度最快的国家之一。轮椅作为老年人和弱势群体的基本代步工具，在他们的日常生活中发挥着重要作用。手动轮椅由于自身的一些缺陷，有被电动轮椅取代的趋势。电动轮椅带有驱动装置，使用者只需操作操纵杆，就可控制轮椅的转动和移动，但电动轮椅是开环控制，严重影响了轮椅的运行精度和稳定性。在这种情况下，智能轮椅应运而生，智能轮椅不仅功能更齐全，运行速度更精确，安全性更高。

对于智能轮椅的速度控制，常用的控制方法是pid控制方法，此方法虽控制简单，稳定性较好，但其随动性较差，特别是当轮椅的运行地面不够平整时，其控制精度往往达不到要求，所以针对智能轮椅，寻求一种兼顾运行稳定性和控制精度的控制方法尤为重要。

技术实现要素：

本发明的目的是克服现有技术的不足，提供一种用于智能轮椅的神经网络pid滑模控制系统，pid滑模的加入可以提高智能轮椅的稳态精度，使智能轮椅具有良好的动态和静态品质。

为了解决上述技术问题，本发明提供了一种用于智能轮椅的神经网络pid滑模控制系统，其特征在于：控制结构包括主控制器、电机驱动模块、带霍尔元件的无刷直流电机、驱动轮和轮椅框架，直流电机与驱动轮固为一体，主控制器发送控制信号给电机驱动模块，通过神经网络pid滑模控制方法来控制直流电机的转速，直流电机上的霍尔元件将电机的实时转速反馈给主控器，形成速度闭环控制系统。

本发明提供的一种用于智能轮椅的神经网络pid滑模控制系统，其神经网络pid滑模控制方法包括步骤：

1）建立直流电机的力学方程；

2）建立神经网络pid滑模控制系统，基于神经网络pid滑模控制设计控制律，将其作为直流电机的控制输入。包括如下步骤：

2-1）设计pid滑模面为：；

其中,是直流电机位置输出的跟踪误差。是直流电机速度的跟踪误差。，为滑模系数，且他们都为正常数；

2-2）设计神经网络pid滑模控制律，使直流电机实际轨迹跟踪上理想轨迹；

其中，该控制器为：

式中，是机械系数;是阻尼系数，,,分别是所述转子的旋转位置，转子的旋转速度，转子的旋转加速度，，仅是可测量的，是转动惯量，是正常数；

3）采用lyapunov函数理论，设计自适应律，验证所述神经网络pid滑模控制系统的渐进稳定性。

进一步的，所述步骤1）中，无刷直流电机的力学方程为：

式中，是机械系数;是阻尼系数，,,是所述转子的旋转位置，转子的旋转速度，转子的旋转加速度，分别，,仅是可测量的，是转动惯量;是负载转矩和干扰转矩的总和。

进一步的，所述步骤2）中神经网络用来估计负载转矩和干扰力矩的总和，设计为：，为映射误差。

进一步的，所述lyapunov函数设计为：，所述自适应率设计为：。

其中，是学习速率，是神经网络中的权重向量，是高斯函数，是被估计的权重向量，是被估计的权重向量的误差，。

实施本发明，具有如下有益效果：1、一种用于智能轮椅的神经网络pid滑模控制系统，由于滑动模态可以进行设计且与直流电机的参数及扰动无关，这就使得滑模控制具有快速响应，对参数变化及扰动不灵敏，物理实现简单等优点。这种控制方法通过控制量的切换使系统状态沿着滑模面滑动，使智能轮椅的控制系统在受到参数摄动和外界干扰的时候具有不变性。

2、pid滑模的加入可以提高智能轮椅控制系统的稳态精度，使智能轮椅具有良好的动态和静态品质。

3、基于李雅普诺夫稳定性理论设计自适应律，实现了参数的在线更新，能够在任意初始值的情况下，保证智能轮椅控制系统的全局渐进稳定性。

附图说明

图1为本发明的智能轮椅控制系统原理方框图。

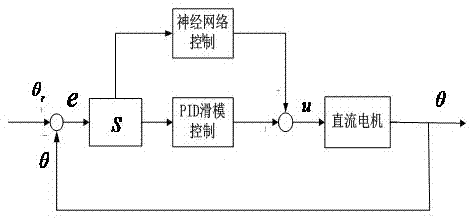
图2为本发明中无刷直流电机控制框图。

具体实施方式

为了便于对本发明的理解，对此作进一步说明。

本发明提供了一种用于智能轮椅的神经网络pid滑模控制系统，图1为本发明智能轮椅控制系统原理方框图，其特征在于：控制结构包括主控制器、电机驱动模块、带霍尔元件的无刷直流电机、驱动轮和轮椅框架，直流电机与驱动轮固为一体，主控制器发送控制信号给电机驱动模块，通过神经网络pid滑模控制方法来控制直流电机的转速，同时，直流电机上的霍尔元件将电机的实时转速反馈给主控器，形成速度闭环控制系统。

图2为本发明智能轮椅的无刷直流电机控制框图，采用神经网络pid滑模控制方法，包括如下步骤：

1.建立无刷直流电机的力学方程：

.（1）

式中，是机械系数;是阻尼系数，,,是所述转子的旋转位置，转子的旋转速度，转子的旋转加速度，分别，,仅是可测量的，是转动惯量;是负载转矩和干扰转矩的总和；

2．建立神经网络pid滑模控制系统，基于神经网络pid滑模控制设计控制律，将其作为直流电机的控制输入。

定义跟踪误差为：.（2）

其中，为位置指令，为直流电机转子的实际旋转位置。

设计pid滑模面，使它所确定的滑动模态渐进稳定且具有良好的动态品质。s设计为：(3)

其中,是直流电机位置输出的跟踪误差，是速度的跟踪误差，，为滑模系数，且他们都为正常数。

设计神经网络pid滑模控制律，使直流电机实际轨迹跟踪上理想轨迹。

其中，该控制器为：

.（4）

式中，是机械系数;是阻尼系数，,,是所述转子的旋转位置，转子的旋转速度，转子的旋转加速度，,仅是可测量的，是转动惯量,是正常数。

3．采用lyapunov函数理论，设计自适应律，验证所述神经网络pid滑模控制系统的渐进稳定性。

lyapunov函数设计为：

.（5）

其中，是学习速率，是神经网络中的权重向量，是高斯函数。是被估计的权重向量，是被估计的权重向量的误差，。

对pid滑模面求导，得到：

.（6）

神经网络用来估计负载转矩和干扰力矩的总和，设计为：

.（7）

其中，为神经网络的映射误差。

将神经网络pid滑模控制律式（4）作为直流电机的控制输入带入式（6），得到

.（8）

那么

.（9）

自适应率设计为：

.（10）

则有：

.（11）

因为，都为正数，是半负定的，所以该智能轮椅的控制系统是稳定的。

本发明提供的一种用于智能轮椅的神经网络pid滑模控制系统，由于滑动模态可以进行设计且与直流电机的参数及扰动无关，这就使得滑模控制具有快速响应，对参数变化及扰动不灵敏，物理实现简单等优点。这种控制方法通过控制量的切换使系统状态沿着滑模面滑动，使智能轮椅的控制系统在受到参数摄动和外界干扰的时候具有不变性。pid滑模的加入可以提高智能轮椅控制系统的稳态精度，使智能轮椅具有良好的动态和静态品质。基于李雅普诺夫稳定性理论设计自适应律，实现了参数的在线更新，能够在任意初始值的情况下，保证智能轮椅控制系统的全局渐进稳定性。