一种在随机非线性系统中补偿丢失信息的方法与流程

本发明涉及自动控制领域的一种在随机非线性系统中补偿丢失信息的方法。

背景技术：

在过去的几十年里，随机系统在各方面都取得了广泛的应用，随机系统鲁棒性和稳定性等方面的研究得到了长足的进步。目前对于随机系统的热点在对于线性随机系统在有限时间内的稳定性。线性随机系统在有限时间内的稳定性是指在一个给定的有限时间周期内，所有允许的输入扰动都不会使其输出超过给定的上限阈值。随着通信网络的飞速发展，越来越多的信息是通过通信网络进行传递的。将通信网络引入反馈控制环以后将发生一些问题，其中测量数据的数据包丢失被视为控制系统性能恶化的主要因素。目前涉及到测量数据的数据包丢失的随机系统在有限时间稳定性的研究几乎为没有，而同步考虑非线性随机系统在有限时间稳定性和测量数据的数据包丢失将使问题更加复杂。

技术实现要素：

本发明的目的是为了克服现有技术的不足，提供一种在随机非线性系统中补偿丢失信息的方法，实现了对受状态依赖性噪声影响的离散时间非线性系统，在有测量数据的数据包丢失时的有效补偿和控制，而且运行稳定可靠。

实现上述目的的一种技术方案是：一种在随机非线性系统中补偿丢失信息的方法，包括下列步骤：

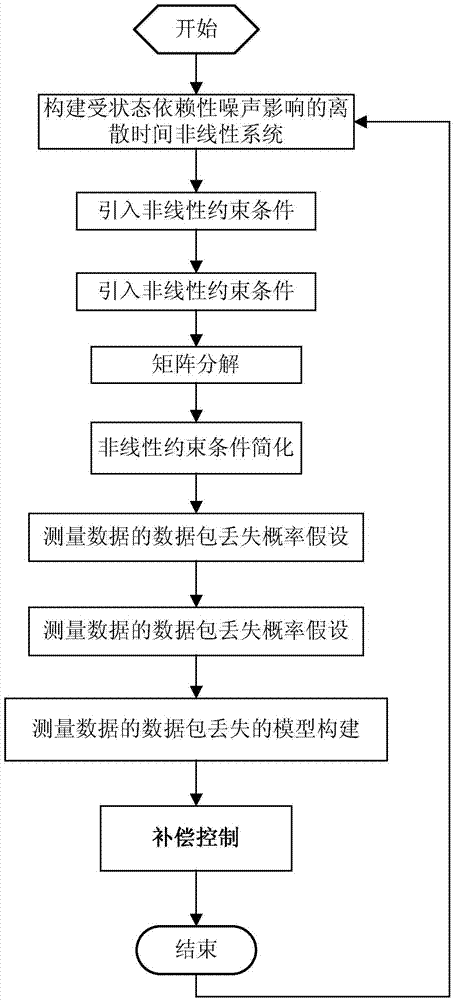
构建受状态依赖性噪声影响的离散时间非线性系统步骤：

对一个受状态依赖性噪声影响的离散时间非线性系统；

其中是系统状态，为控制输入量，为系统输出量，ε{ωk}＝0，当i≠j时ε{ωiωj}＝0，矩阵和矩阵是已知的，为外来干扰量，满足其中σ为一个恒定的自然数；

引入非线性约束条件步骤：

当k∈n0时，对于未知的非线性函数满足下列的二次曲面的约束条件的空间：

其中均是未知的；

矩阵分解步骤：

将分解为：

其中，δc(k)和δf(k)未知的随时间变换矩阵函数，并满足δc(k)≤1，δf(k)≤1，矩阵a、b、f、af、bf、ff是已知的；

测量数据的数据包丢失概率假设步骤：

随机变量θk表征发生状态测量数据丢失的概率，并符合贝努利过程：

其中表示任意一个数据包丢失的可能性，表示状态数据成功通过通信网络完成了传递；

测量数据的数据包丢失的模型构建步骤：

给以一个标量β〉0和一个迭代补偿常数n，以及一个矩阵r〉0，随机非线性系统对于(σ,β,n,r)是一个在有限时间内稳定的系统，如果任何外来扰动满足即有：

补偿控制步骤：

其中

并在k＝0，

令其中k为矩阵放大增益。

进一步的，所述矩阵分解步骤和所述测量数据的数据包丢失概率假设步骤之间还设有非线性约束条件简化步骤，将二次曲面的约束条件曲线边界的约束条件或标准的lipschitz约束条件。

进一步的，没有测量数据的数据包丢失时，状态的估计值是收到的数据。

采用了本发明的一种在随机非线性系统中补偿丢失信息的方法的技术方案，通过依次进行的构建受状态依赖性噪声影响的离散时间非线性系统步骤、引入非线性约束条件步骤、矩阵分解步骤、测量数据的数据包丢失概率假设步骤和补偿控制步骤，实现了对受状态依赖性噪声影响的离散时间非线性系统，在有测量数据的数据包丢失时的有效补偿和控制，而且运行稳定可靠。

附图说明

图1为本发明的一种在随机非线性系统中补偿丢失信息的方法的流程图。

图2为本发明的一种随机非线性系统用补偿控制器的结构图。

具体实施方式

请参阅图1，本发明的发明人为了能更好地对本发明的技术方案进行理解，下面通过具体地实施例，并结合附图进行详细地说明：

若是一个可能性空间。ω是样本空间,f是样本空间子集的σ代数，是可能性的测量，ε{·}表示关于可能性的测量，是期望算符。m＞0表示m是个正定矩阵，m<0表示m一个负定矩阵，记号p＞q表示矩阵p-q＞0.||·||表示向量的欧几里得范数或者向量的谱范数在对称的矩阵中”★”用来表示对称矩阵中主对角线下方的元素，对于给定的矩阵a，令he{a}＝a+a^t。

本发明的一种在随机非线性系统中补偿丢失信息的方法是通过一个随机非线性系统用补偿控制器完成的。该补偿控制器包括控制输入单元1、控制输出单元2、误差输入单元3、补偿单元4、系统构建单元5、约束条件输入单元6、矩阵分解单元7、约束条件简化单元8和数据包丢失模型单元9构成的。

构建受状态依赖性噪声影响的离散时间非线性系统步骤：

对一个受状态依赖性噪声影响的离散时间非线性系统；

其中是系统状态，为控制输入量，为系统输出量，ωk是一个在指定的可能性空间内的标准一维布朗运动，该可能性空间与σ代数的一个单调递增向量族(fk)k∈n相关，该单调递增向量族(fk)k∈n是由其中为自然数。因此可以假设ε{ωk}＝0，当i≠j时ε{ωiωj}＝0。矩阵和矩阵是已知的，外来干扰量满足其中σ为一个恒定的自然数。

其中控制输入量是通过该补偿控制器中的控制输入单元1输入的，系统输出量是通过该补偿控制器中的控制输出单元2输出的。外来干扰量是通过该补偿控制器中该误差输入单元3输入的，系统状态是通过该补偿控制器的补偿单元4进行存储和计算的。该受状态依赖性噪声影响的离散时间非线性系统是通过该补偿控制器中的系统构建单元5构建的。

引入非线性约束条件步骤：

当k∈n0时，对于未知的非线性函数满足下列的二次曲面的约束条件的空间：

该步骤是通过该补偿控制器的约束条件输入单元6进行的。

矩阵分解步骤：

对于含有未知量的矩阵均可分解成如下形式：

其中，δc(k)和δf(k)未知的随时间变换矩阵函数，并满足δc(k)≤1，δf(k)≤1，矩阵a、b、f、af、bf、ff是已知的。

该步骤是通过该补偿控制器的矩阵分解单元7进行的。

非线性约束条件简化步骤：

需要指出的是许多非线性条件都属于二次曲面的约束条件。比如对于未知函数f(xk,uk,dk)在空间(uk,dk)内是自由的，则约束条件的空间：

可变化为：其等价于：

[f(xk)-(a+af)xk]^t[f(xk)-(a+af)xk]≤0；

这样二次曲面的约束条件被简化为曲线边界的约束条件。

此外，二次曲面的约束条件的空间：

的中心源自于一个n维超球空间，且在该二次曲面的约束条件的空间的右侧不存在控制输入量和外来干扰量，则该二次曲面的约束条件的空间可以简化为标准的lipschitz约束条件，即(f(0)≡0)。

该步骤是通过该补偿控制器的约束条件简化单元8进行的。

测量数据的数据包丢失概率假设步骤：

传感器和补偿控制器之间在通过通信网路传递状态的测量数据的过程中，会出现测量数据的数据包的丢失，在补偿控制器设计过程中必须考虑测量数据的数据包丢失的影响。本发明中，随机变量θk表征发生状态测量数据丢失的概率，并符合贝努利过程。

其中表示任意一个数据包丢失的可能性，表示状态数据成功通过通信网络完成了传递。

测量数据的数据包丢失的模型构建步骤：

描述通信网络中数据包丢失的模型很多，本发明的一种在随机非线性系统中补偿丢失信息的方法适用测量数据的数据包连续丢失的情况。本发明的一种在随机非线性系统中补偿丢失信息的方法中，对于输入输出在有限时间内稳定的随机非线性系统：

给以一个标量β＞0和一个迭代补偿n，以及一个矩阵r＞0，随机非线性系统对于(σ,β,n,r)是一个在有限时间内稳定的系统，如果任何外来扰动满足即有：

令和φk为在相应维度内的实矩阵，则对于任意标量∈＞0，都有

对于任意标量，∈＞0和矩阵p＞0，都有：

其中，为闭环系统中定义的非线性函数。

上述两个步骤是通过该补偿控制器中的数据包丢失模型单元9进行的。

补偿控制步骤：通过该补偿控制器中的补偿单元4进行的，其采用的补偿策略为：

其中构建的补偿为

为了实际应用的需要，在开始迭代时，令k＝0，

通过所述补偿，构建一个状态反馈：

其中k为矩阵放大增益，必须说明的是即使没有测量数据的数据包丢失，状态的估计值也是所述补偿控制器所能收到的数据。否则的话，在k-1步骤中的状态的估计值会被自动默认为代入：

可得:

其中：

本技术领域中的普通技术人员应当认识到，以上的实施例仅是用来说明本发明，而并非用作为对本发明的限定，只要在本发明的实质精神范围内，对以上所述实施例的变化、变型都将落在本发明的权利要求书范围内。