基于空间圆弧近似的轮廓误差实时估计方法与流程

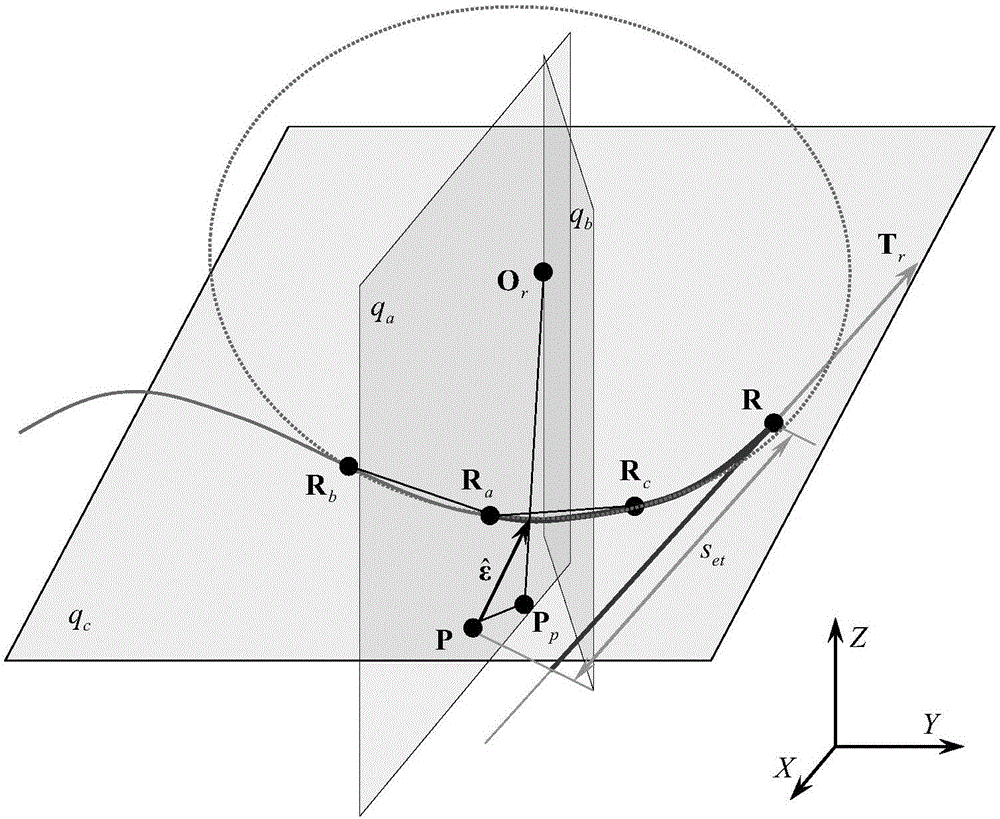
本发明属于精密高效数控加工
技术领域：
，涉及一种样条曲线插补加工过程中基于空间圆弧近似的轮廓误差实时估计方法。
背景技术：
：随着高端装备领域的快速发展，复杂曲面零件的高速数控加工技术应用越来越广。鉴于复杂曲面零件加工刀轨多为具有复杂几何特征的曲线，采用传统的直线、圆弧插补数控加工时，由于直线、圆弧段逼近理想曲线时一阶不连续点的存在，会导致数控加工过程中进给轴的频繁加减速，影响加工质量和加工效率。参数样条曲线直接插补技术可克服传统直线、圆弧插补加工的缺陷，因此得到了广泛研究。然而，在参数曲线直接插补过程中，由于各进给轴伺服控制系统的滞后特性及动态性能不匹配等原因，会引起较大的加工轨迹轮廓误差，且该误差随着进给速度的增加而增大，从而降低了复杂曲面零件的加工精度。为解决这一问题，国内外学者提出了一系列先进的控制算法，交叉耦合控制是其中的典型代表。交叉耦合控制器主要由轮廓误差估计算法和控制律构成，因此，高精度的轮廓误差估计是保障交叉耦合控制器性能进而提高数控系统轮廓跟踪精度的前提。综上，研究参数样条曲线插补加工过程中轮廓误差的实时高精度估计方法对实现复杂曲面零件的高效精密数控加工具有重要意义。文献“ANovelContourErrorEstimationforPositionLoop-BasedCross-CoupledControl”，Yang等，IEEE/ASMETransactionsonMechatronics，2011，16(4)：643-655，该文献提出一种基于密切圆弧近似的轮廓误差估计方法，然而，该方法只适用于二维平面轮廓，且当随动误差较大时估计精度较低；文献“AReal-timecontouringerrorestimationformulti-axismotionsystemsusingthesecond-orderapproximation”，Zhu等，InternationalJournalofMachineToolsandManufacture，2013，68：75-80，该文献提出一种基于点到曲线距离公式的二阶近似空间轮廓误差实时估计方法，然而该方法当随动误差较大时估计精度同样较低，且估计算法获得的为实际点到理想曲线的距离值，而非轮廓误差矢量值。技术实现要素：本发明旨在克服现有技术缺陷，发明一种适用于参数样条曲线插补器的空间轮廓误差实时估计方法，该方法基于一阶泰勒级数展开法计算参数曲线上用于拟合空间圆弧的特征点，并构造空间圆弧近似替代理想轮廓，从而计算轮廓误差矢量值，实现空间轮廓误差的高精度估计。本发明的技术方案是一种基于空间圆弧近似的轮廓误差实时估计方法，其特性在于，该方法基于一阶泰勒级数展开法计算参数样条曲线上用于轮廓误差估计的特征点，再根据特征点拟合空间圆弧，并获得其圆心坐标；最后，根据实际加工点与所拟合空间圆弧的位置关系，计算轮廓误差矢量估计值；方法的具体步骤如下：第一步计算特征点设参数样条曲线的方程为C＝C(u)，其中u为曲线参数，当前理想刀位点为R，对应的曲线参数值为ur，实际刀位点为P，则随动误差向量Et为：Et＝R-P(1)为全面反映实际刀位点P附近理想曲线形貌，以随动误差向量在曲线当前理想刀位点处的切线方向上的投影长度为基准，根据一阶泰勒级数展开法，确定参数曲线上用于空间圆弧拟合的第一个特征点Ra，以投影长度的1.5倍为基准，确定第二个特征点Rb，以投影长度的0.5倍为基准，确定第三个特征点Rc；Ra点处曲线参数ua的计算方法为：ua=ur-duds|u=urEt·Tr---(2)]]>其中，s为曲线弧长，Tr为理想刀轨在R点处的单位切失，参数u对s的导数为：duds|u=ur=1dsdu|u=ur=1||C′(ur)||---(3)]]>其中，C′(ur)为参数方程C(u)对参数u的导矢在ur处的值；Tr为：Tr=C′(ur)||C′(ur)||---(4)]]>将公式(1)、(3)、(4)带入公式(2)得：ua=ur-(R-P)·C′(ur)||C′(ur)||2---(5)]]>因此Rb点处曲线参数ub为：ub=ur-32duds|u=urEt·Tr=3ua-ur2---(6)]]>Rc点处曲线参数uc为：uc=ur-12duds|u=urEt·Tr=ua+ur2---(7)]]>因此Ra、Rb、Rc点分别计算为Ra＝C(ua)，Rb＝C(ub)及Rc＝C(uc)；根据特征点Ra、Rb及Rc实现空间圆弧的拟合；第二步拟合空间圆弧通过Ra、Rb和Rc三点所确定空间圆的圆心为线段RaRb的中垂面qa、线段RaRc的中垂面qb以及Ra、Rb、Rc三点所确定的平面qc三个平面的交点，其中，平面qa的表达式为：(Ra-Rb)·xyz=(Ra-Rb)·(Ra+Rb)2---(8)]]>式中，(x,y,z)为平面上任一点的坐标值；平面qb的表达式为：(Rc-Ra)·xyz=(Rc-Ra)·(Rc+Ra)2---(9)]]>平面qc的表达式为：(Rb-Rc)×(Ra-Rb)·xyz=(Rb-Rc)×(Ra-Rb)·Rc---(10)]]>设拟合空间圆的圆心为Or＝[OxrOyrOzr]T，则其必满足公式(8)、(9)和(10)，因此圆心坐标计算为：Or=12·(Ra-Rb)T(Rc-Ra)T((Rb-Rc)×(Ra-Rb))TT.(Ra-Rb)·(Ra+Rb)(Rc-Ra)·(Rc+Ra)2(Rb-Rc)×(Ra-Rb)·Rc---(11)]]>所构造的空间圆弧即为以Or为圆心，以||Ra-Or||为半径的在平面qc上的圆；第三步计算轮廓误差矢量估计值令轮廓误差估计值为实际刀位点P到第二步中所构造空间圆弧的距离；因空间圆所在平面为qc，设qc面的单位法矢为nc，则：nc=(Rb-Rc)×(Ra-Rb)||(Rb-Rc)×(Ra-Rb)||---(12)]]>P点在qc平面上的投影点Pp为：Pp＝P-(nc·(P-Ra))nc(13)将公式(12)代入(13)得Pp点为：Pp=P-((Rb-Rc)×(Ra-Rb)·(P-Ra))||(Rb-Rc)×(Ra-Rb)||2(Rb-Rc)×(Ra-Rb)---(14)]]>将轮廓误差矢量的估计值表示为则根据实际刀位点P与拟合空间圆Or的几何关系确定其计算公式为：ϵ^=(||R1-Or||||Pp-Or||-1)(Pp-Or)+Pp-P---(15)]]>在数控系统的每个插补周期内，根据插补器提供的参数曲线几何信息及实际刀位点坐标，执行上述步骤实现每一点处轮廓误差矢量值的实时估计。本发明的有益效果是：建立了基于空间圆弧近似的轮廓误差估计模型，为参数曲线插补空间轨迹加工轮廓误差的实时高精度估计提供了有效途径；在估计轮廓误差时充分考虑了实际刀位点附近的理想刀轨形貌，在随动误差较大时亦可保证轮廓误差的估计精度。附图说明图1—空间刀轨轮廓几何模型图。图2—轮廓误差估计方法示意图，其中，R为理想刀位点，P为实际刀位点，Tr为理想刀轨在R点处的单位切失，set为随动误差在Tr方向上的投影长度，Ra为第一个特征点，Rb为第二个特征点，Rc为第三个特征点，qa为线段RaRb的中垂面，qb为线段RaRb的中垂面，qc为Ra、Rb、Rc三点确定的平面，Or为拟合空间圆的圆心，Pp为P点在qc平面上的投影点，为轮廓误差矢量的估计值。图3—本方法估计轮廓误差与实际轮廓误差的偏差图，其中，X轴表示插补周期序号，Y轴表示偏差值，单位为mm。图4—Zhu等人方法估计轮廓误差与实际轮廓误差的偏差图；其中，X轴表示插补周期序号，Y轴表示偏差值，单位为mm。具体实施方式结合技术方案与附图详细说明本发明的具体实施方式。在参数样条曲线直接插补过程中，由于各进给轴伺服控制系统的滞后特性及动态性能不匹配等原因，会引起较大的加工轨迹轮廓误差，为提高加工轮廓精度，需在实时估计轮廓误差的基础上，进行轮廓控制。据此，发明一种基于空间圆弧近似的高精度轮廓误差实时估计方法。附图1为空间刀轨轮廓几何模型图，以附图1所示的非均匀有理B样条空间刀轨轮廓为例，详细说明本发明具体实施过程，该空间刀轨轮廓的非均匀有理B样条参数为：阶数：2；控制点：{(0,0,0)；(-8,-20,0)；(30,-5,-5)；(60,-20,0)；(47,0,0)；(60,20,0)；(30,5,-5)；(-8,20,0)；(0,0,0)}；权因子：{1,0.9,0.75,1.5,6,3.5,1.8,1.5,1}；节点向量：{0,0,0,0.15,0.3,0.45,0.6,0.75,0.85,1,1,1}。借助MATLAB/SIMULINK数值仿真平台，建立三轴数控机床进给伺服控制系统模型，X轴进给控制系统的传递函数Gx(s)为：Gx(s)=6751.8S2+91.24s+6751.8---(16)]]>Y轴进给控制系统的传递函数Gy(s)为：Gy(s)=6478.1S2+91.24s+6478.1---(17)]]>Z轴进给控制系统的传递函数Gz(s)为：Gz(s)=7116.8S2+91.24s+7116.8---(18)]]>根据二阶泰勒级数展开法对附图1所示空间刀轨轮廓进行曲线插补，并在每一个插补周期内依据理想刀位点R、实际刀位点P以及轮廓曲线参数信息，利用本方法实时估计轮廓误差；附图2为轮廓误差估计方法示意图，实施的具体过程如下：第一步，计算特征点：根据公式(5)、(6)、(7)计算特征点参数ua、ub、uc，进而获得三个特征点Ra、Rb和Rc；第二步，拟合空间圆弧：根据第一步中获得的特征点Ra、Rb和Rc，利用公式(8)、(9)、(10)获得线段RaRb的中垂面qa、线段RaRc的中垂面qb以及Ra、Rb、Rc三点所确定平面qc，进而利用公式(11)计算通过三个特征点的空间圆弧圆心Or坐标；第三步，计算轮廓误差矢量估计值：根据公式(14)计算实际刀位点P在圆弧所在平面qc上的投影Pp，进而利用公式(15)获得轮廓误差矢量的估计值在每个插补周期内重复上述步骤，即可得到每个插补点处的轮廓误差估计值，另外，利用离线非实时方法计算实际轮廓误差真值，将本方法估计的轮廓误差值与实际误差值对比，得到二者偏差如附图3所示；为说明本发明在轮廓误差估计精度方面的优势，同样采用Zhu等人在文献“AReal-timecontouringerrorestimationformulti-axismotionsystemsusingthesecond-orderapproximation”，Zhu等，InternationalJournalofMachineToolsandManufacture，2013，68：75-80，中提出的基于点到曲线距离公式的二阶空间轮廓误差估计方法进行轮廓误差估计，并将该方法的估计值与实际误差值对比，得到偏差如附图4所示；对比附图3和附图4可见，本方法的估计偏差最大值为0.0093mm，Zhu等人方法的估计偏差最大值为0.0899mm，说明了采用本方法可有效提高轮廓误差估计精度，具有良好的轮廓误差估计效果。本发明面向参数样条曲线插补实际加工中对产生的轮廓误差进行补偿与控制时高精度估计轮廓误差的重大需求，发明了基于空间圆弧近似的轮廓误差实时估计方法，对数控机床进给伺服系统轮廓跟踪精度的提高具有重大意义。当前第1页1 2 3