一种基于模糊自适应PID的高阶控制系统稳定性判定方法与流程

本发明属于模糊控制
技术领域：
，尤其涉及一种基于模糊自适应PID的高阶控制系统稳定性判定方法。
背景技术：
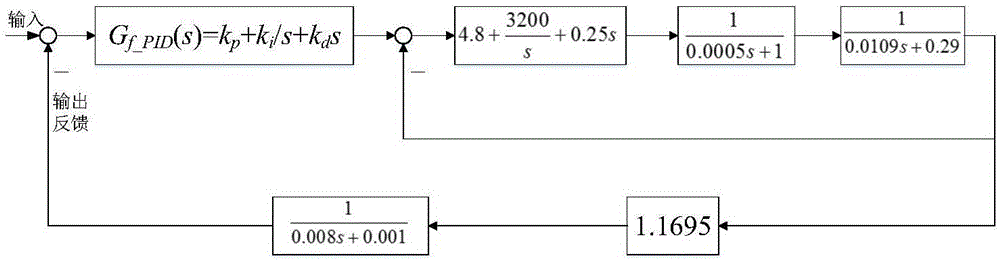
：目前，基于模糊自适应PID的控制系统已经在工业过程、家电控制、水电控制等领域取得了应用。基于模糊自适应PID的控制系统中含有一个或多个模糊自适应PID控制器，是模糊控制系统的重要组成部分，但是模糊自适应PID控制器本身是非线性的，并且没有统一的系统描述方式，研究人员很难将经典控制理论推广到其设计与分析过程中，现代控制理论提出了一些解决该问题的思想与方法，文献《解析模糊控制理论：模糊控制系统稳定性分析》中提到了Lyapunov稳定性理论，小增益理论，相平面分析法和基于滑模变结构系统分析方法等，然而，这些方法常用作指导理论来设计稳定的模糊控制器，具有先验性功能，如果采用这些方法对模糊控制系统进行稳定性判定则有以下缺点：首先，一般采用何种方法进行模糊控制器设计，也只能采用何种方法进行系统的稳定性判定，因此，不具有普适应，后验性功能差；其次，这些方法的实施过程都比较复杂。技术实现要素：要解决的技术问题为解决基于模糊自适应PID的高阶控制系统稳定性判定困难的问题，本发明提出一种基于模糊自适应PID的高阶控制系统稳定性判定方法，该方法根据高阶控制系统的特征方程和模糊自适应PID控制器参数的取值范围，利用随机搜索法求得特征根，并根据特征根对系统稳定性作出判定。技术方案一种基于模糊自适应PID的高阶控制系统稳定性判定方法，其特征在于步骤如下：步骤1：确定系统特征方程：根据系统的开环传递函数G(s)得到系统的特征方程D(s)＝fn(kp,ki,kd)sn+fn-1(kp,ki,kd)sn-1+……+f1(kp,ki,kd)s+f0(kp,ki,kd)＝0；其中，G(s)＝Gf_PID(s)·F(s)，为模糊自适应PID控制器的传递函数，F(s)为系统中除模糊自适应PID控制器之外其它部分的传递函数，kp为模糊自适应PID控制器的比例系数，ki为模糊自适应PID控制器的积分系数，kd为模糊自适应PID控制器的微分系数，f0(kp,ki,kd)、f1(kp,ki,kd)、…、fn-1(kp,ki,kd)、fn(kp,ki,kd)是特征方程的各项系数；步骤2：确定参数取值范围：按照ap＝x1K′p+kp0计算得到比例系数kp的取值下限ap，按照bp＝x2K′p+kp0计算得到比例系数kp的取值上限bp，则确定比例系数kp的取值范围为[ap，bp]；按照ai＝x1K′i+ki0计算得到积分系数ki的取值下限ai，按照bi＝x2K′i+ki0计算得到积分系数的取值上限bi，则确定积分系数ki的取值范围为[ai，bi]；按照ad＝x1K′d+kd0计算得到微分系数kd的取值下限ad，按照bd＝x2K′d+kd0计算得到微分系数kd的取值上限bd，则确定微分系数kd的取值范围为[ad，bd]；其中，x1、x2分别是输出模糊论域的下限和上限，K′p、K′i、K′d分别是比例系数、积分系数和微分系数对应的输出比例因子，kp0、ki0、kd0分别是比例系数、积分系数和微分系数的初始值；步骤3：稳定性判定：1)采用随机搜索法在比例系数kp、积分系数ki和微分系数kd的取值范围内搜索得到n组不同的值Xj＝(kpj，kij，kdj)；其中n≥800；j＝1,…,n；kpj∈[ap,bp]，kij∈[ai,bi]，kdj∈[ad,bd]；2)将这n组不同的值分别代入步骤一得到的系统特征方程，解特征方程，得到其特征根，如果存在某组值使得某个特征根的实部大于0，则判定系统不稳定；否则，利用随机搜索法分别在使得特征根实部取值最大的三组值Xa＝(kpa，kia，kda)、Xb＝(kpb，kib，kdb)、Xc＝(kpc，kic，kdc)的附近范围内搜索，分别得到m组不同的值Xaz＝(kpaz，kiaz，kdaz)、Xbz＝(kpbz，kibz，kdbz)、Xcz＝(kpcz，kicz，kdcz)；其中，m≥800；z＝1,…,m；Xa、Xb、Xc的附近范围分别为[0.9Xa,1.1Xa]，[0.9Xb,1.1Xb]，[0.9Xc,1.1Xc]，即kpaz∈[0.9kpa,1.1kpa]，kiaz∈[0.9kia,1.1kia]，kdaz∈[0.9kda,1.1kda]，kpbz∈[0.9kpb,1.1kpb]，kibz∈[0.9kib,1.1kib]，kdbz∈[0.9kdb,1.1kdb]，kpcz∈[0.9kpc,1.1kpc]，kicz∈[0.9kic,1.1kic]，kdcz∈[0.9kdc,1.1kdc]；将这3m组不同的值分别代入步骤一得到的系统特征方程，解特征方程，得到其特征根，如果存在某组值使得某个特征根的实部大于0，则判定系统不稳定；否则，判定系统稳定。有益效果本发明提出一种基于模糊自适应PID的高阶控制系统稳定性判定方法，将模糊自适应PID控制器看成参数可变的传统PID控制器，首先确定系统的特征方程和模糊自适应PID控制器参数的取值范围，然后根据特征根进行稳定性判定，方法简单且能对任意基于模糊自适应PID的系统进行稳定性判定，具有后验性功能。此外，采用随机搜索法很好地解决了高阶控制系统特征方程没有通解的问题，简单高效。附图说明图1是本发明的一种基于模糊自适应PID的高阶控制系统稳定性判定方法的基本流程图。图2是基于模糊自适应PID的高阶控制系统结构框图。图3是随机搜索法算法框图。具体实施方式下面结合附图和实施例对本发明进一步说明，本发明包括但不仅限于下述实施例。本发明提出一种基于模糊自适应PID高阶控制系统的稳定性判定方法，结合模糊自适应PID控制器的特点和经典控制理论对已有高阶控制系统的稳定性进行判定，如图1所示，其具体步骤如下：1)确定系统的特征方程本实施例的基于模糊自适应PID的高阶控制系统结构框图如图2所示，将其模糊自适应PID控制器看成参数可变的传统PID控制器，即传递函数为Gf_PID(s)＝kp+ki/s+kds。其中，kp、ki和kd分别为模糊自适应PID控制器的比例系数、积分系数和微分系数，这些参数在工作过程中无规律变化。根据系统的结构框图可以写出其开环传递函数为：0.292kds4+(5.614kd+0.292kp)s3+(3742.4kd+5.614kp+0.292ki)s2D(s)=+(3742.4kp+5.614ki)s+3742.4ki4.36×10-8s5+0.002s4+0.041s3+25.605s2+3.2s---(1)]]>则系统的特征方程为：D(s)=4.36×10-8s5+(0.292kd+0.002)s4+(5.614kd+0.292kp+0.041)s3+(3742.4kd+5.614kp+0.292ki+25.605)s2+(3742.4kp+5.614ki+3.2)s+3742.4ki=0---(2)]]>可以看出，系统特征方程是关于变量kp、ki、kd的5阶方程。2)确定kp、ki、kd的变化范围模糊自适应PID控制器参数kp、ki、kd的变化范围分别等于各参数初始值kp0、ki0、kd0加上其校正量kp*、ki*、kd*，而校正量kp*、ki*、kd*的大小由输出模糊论域[x1,x2]和相应的输出比例因子K′p、K′i、K′d决定。具体为：按照ap＝x1K′p+kp0计算得到比例系数kp的取值下限ap，按照bp＝x2K′p+kp0计算得到比例系数kp的取值上限bp，则确定比例系数kp的取值范围为[ap，bp]；按照ai＝x1K′i+ki0计算得到积分系数ki的取值下限ai，按照bi＝x2K′i+ki0计算得到积分系数的取值上限bi，则确定积分系数ki的取值范围为[ai，bi]；按照ad＝x1K′d+kd0计算得到微分因子kd的取值下限ad，按照bd＝x2K′d+kd0计算得到微分因子kd的取值上限bd，则确定微分因子kd的取值范围为[ad，bd]；本实施例中输出模糊论域是[-1,1]，输出比例因子分别为K′p＝51，K′i＝0.3，K′d＝0.15，各参数初始值分别为kp0＝85，ki0＝0.5，kd0＝0.25，那么模糊自适应PID控制器各参数的取值范围为：kp∈[34,136]，ki∈[0.2,0.8]，kd∈[0.1,0.4]。3)采用随机搜索法取点，对系统稳定性作出判断根据经典控制理论，如果可以求出系统特征方程的根，且特征方程的根的实部都小于0，则系统稳定。由系统特征方程(公式(2))可以看出，由于是5阶的，且kp、ki、kd不断变化，并没有通解。需要寻找一种直接解方程以外的方式来解决这个问题。kp、ki、kd的变化范围已知，在变化范围内每取一组kp、ki和kd，特征方程会求得对应的特征根，对比所有特征根的实部，如果能找到一组kp、ki和kd使得某个特征根的实部大于0，则系统并不是完全稳定的，即存在不稳定的因素；如果对任意kp、ki和kd所能寻得的特征根的实部都是小于0的，认为系统是稳定的，此时，原问题转换成在约束条件下寻最大特征根实部的问题，即：f(s)=maxRe(s)s.t.D(s)=034≤kp≤1360.2≤ki≤0.80.1≤kd≤0.4]]>其中，Re(s)为特征根实部，f(s)为最大特征根实部。为解决上述问题，需要采用一种优化方法来寻找满足条件的点，寻优的过程是一种抽样验证的方法，本发明采用较简单的随机搜索法。搜索区间是一个三维空间，向量形式表示为X＝(kp，ki，kd)，假设满足Re(s)>0的X占整个搜索区间的比例为p＝20％，那么不满足的点占整个搜索区间的80％，随机取n个点，遇到满足Re(s)>0的概率为P(f)＝1-0.8n，当n值非常大时，找到最优点的可能性会增大，基于该原理，当满足Re(s)>0的点占整个区域的0.5％以上时，只要实验次数超过1000次，能找到满足条件结果的概率已经超过99％，为避免“弃真”错误，如图3所示，这里采用多次取样的方法：采用随机搜索法给出n＝1000组不同的随机点Xi＝(kpi，kii，kdi)，i＝1,…,n，随机点先由Matlab函数random()产生[0,1]的随机数，再将它们调整到需要范围之内，这样可保证取值的随机性，本实施例中kpi＝34+102*random()，kii＝0.2+0.6*random()，kii＝0.1+0.3*random()；然后，将随机点代入特征方程D(s)中求出所有特征根，如果存存在点Xi使得任意一个特征根实部大于0，直接作出系统会不稳定的判断，原模糊控制系统需要重新设计；如果在上述搜索过程中不存在点Xi使得特征根实部大于0，为避免“误判”情况的发生，再一次采用随机搜索法进行寻优，经过第一次随机搜索之后，在使Re(s)取值最大的前三个点Xa，Xb和Xc附近能寻找到使得maxRe(s)>0的点的概率将大大增加，所以重点在这三个点附近范围(变化±10％)内，利用随机搜索法各取m＝800个点Xaj，Xbj和Xcj，j＝1,…,m，代入特征方程求所有的特征根，如果所有的特征根实部仍然都小于0，则作出系统稳定的判断，否则作出系统会不稳定的判断。由上述过程可以看出，本发明提出的一种基于模糊自适应PID高阶控制系统的稳定性判定方法是一种简单的、具有普适性的后验性判定方法。当前第1页1 2 3