基于生物速度调节的欠驱动AUV三维轨迹跟踪控制方法与流程

本发明涉及的是一种水下无人航行器的运动控制方法，具体地说是一种欠驱动水下无人航行器的运动控制方法。

背景技术：

水下无人航行器(Autonomous underwater vehicle,AUV)的三维空间轨迹跟踪能力是实现海洋资源开发、海底地形勘测等领域重要技术前提。欠驱动AUV只具有纵向推进器，在垂向和横向上缺少推进器，AUV在水下三维空间的六自由度运动形式使得模型具有高度耦合性和非线性特性，加之外界的干扰导致模型参数的不确定性，且还需满足时间与空间上的要求，使得欠驱动AUV的三维轨迹跟踪控制更加难以实现。

目前对于AUV的轨迹和路径跟踪控制的研究方法大多采用反步法设计控制器，反步法在解决不确定非线性系统的控制设计中具有明显优势。反步法采用基于系统分层递推的设计思想，通过分步构造李雅普诺夫能量函数，通过设计中间虚拟控制函数并逐步计算出中间虚拟控制量的导数，然后逐级的引入后续的子系统，实现对前级子系统的镇定，利用这种迭代的思想获得最终的实际控制输入。可直接对虚拟控制量解析求导会导致“计算膨胀”，并且虚拟速度控制都和误差相关，当误差增大时，速度会产生较大的跳变，可能会超出控制力矩的输出范围，导致控制失效。为此本发明将生物启发模型和定义虚拟速度误差变量反步控制方法相结合,利用生物启发模型来调节所设计的速度误差,实现了对速度误差进行一定范围内动态调节的目的。从动力学角度设计了欠驱动AUV三维生物速度调节轨迹跟踪控制器,克服了反步法跟踪控制中拐点处跳变的问题,在保证避免奇异值的同时,增加了系统对拐点跳变的鲁棒性。为了克服传统反步法中的计算量大的缺点，文献《Position-tracking control of underactuated autonomous underwater vehicles in the presence of unknown ocean currents》(IET Control Theory and Applications.2010,第4卷第11期)通过定义虚拟速度误差变量简化了传统反步法中的中间计算过程；文献《欠驱动无人水下航行器三维轨迹跟踪的反步控制》(控制理论与应用.2014,第31卷第11期)提出了定义虚拟速度误差变量的方法,并实现了欠驱动UUV三维轨迹跟踪控制,但该方法为了避免虚拟控制律中分母可能出现的奇异值,降低了系统的控制性能,且文中未对轨迹的直角拐点进行研究处理；文献《An efficient neural network approach to tracking control of an autonomous surface vehicle with unknown dynamics》(Expert Systems with Applications.2013,第40卷第5期)将一种生物启发模型和反步法应用在移动机器人和水面艇中,然而平面移动机器人和水面艇的结构相对简单,控制器的设计较容易；文献《A Bioinspired Filtered Backstepping Tracking Control of 7000-m Manned Submarine Vehicle》(IEEE Transactions on Industrial Electronics.2014,第61卷第7期)将这种生物启发模型应用在全驱动水下航行器中,且该方法只是从运动学的角度起到了平滑与滤波的作用,并未考虑动力学模型的设计；目前还没有相关文献讨论基于生物速度调节的欠驱动AUV三维轨迹跟踪控制设计。

申请人提出的申请号为201610247753.1的专利文件中，公开了《一种基于动态速度调节的欠驱动UUV平面轨迹跟踪控制方法》，改进定义虚拟速度误差变量反步法的控制律，提出利用生物启发模型对速度误差进行动态调节的方法，但该方法只停留在研究平面轨迹跟踪控制上，且只能对光滑的轨迹进行跟踪，实际应用价值有限。

技术实现要素：

本发明的目的在于提供一种速度可调的、避免出现奇异值的基于生物速度调节的基于生物速度调节的欠驱动AUV三维轨迹跟踪控制方法。

本发明的目的是这样实现的：

步骤1、AUV根据当前任务，给定一个期望状态X_d(t)＝[x_d(t),y_d(t),z_d(t),θ_d(t),ψ_d(t)]^T，并通过所搭载的导航设备和传感器获取AUV的实际状态X(t)＝[x(t),y(t),z(t),θ(t),ψ(t)]^T和速度V(t)＝[u(t),v(t),ω(t),q(t),r(t)]^T信息，其中x_d(t),y_d(t),z_d(t)和θ_d(t),ψ_d(t)为地面坐标下AUV的期望位置与姿态，x(t),y(t),z(t)和θ(t),ψ(t)为地面坐标下AUV的实际位置和姿态，u(t),v(t),ω(t)和q(t),r(t)为船体坐标系下的线速度和角速度；

步骤2、利用步骤1中的得到的AUV实际状态，通过欠驱动AUV的数学模型和轨迹跟踪位置误差模型，计算出实际轨迹与期望轨迹之间的位置误差和姿态误差，将地面坐标信息转换为船体坐标信息；

步骤3、基于步骤2中计算出的位置和姿态误差，采用定义虚拟速度误差变量的方法，将姿态跟踪控制转化为速度控制，计算出纵向速度虚拟控制律u_d、纵倾角速度虚拟控制律q_d和艏摇角速度虚拟控制律r_d；

步骤4、计算得出纵向速度误差e_u，纵倾角速度误差e_q和艏摇角速度误差e_r，并将这三个误差分别通入生物启发模型，通过设置生物启发模型中的参数，完成对速度误差的动态调节；

步骤5、根据给定的数学模型和步骤4中经动态调节后得到的输出量，推导欠驱动AUV三维轨迹跟踪的动态速度调节控制器，包括纵向控制力矩τ_u的控制信号、纵倾控制力矩τ_q和艏摇控制力矩τ_r的控制信号，并对当前环境扰动进行估计设计了自适应控制律，实现在外界常值扰动下对欠驱动AUV三维轨迹跟踪控制。

本发明还可以包括：

1、所述欠驱动AUV的数学模型包括运动学模型、动力学模型、轨迹跟踪误差模型、位置误差以及期望姿态，表达式分别为:

运动学模型：

动力学模型：

其中：d₂₂＝Y_v+Y_v|v||v|；d₃₃＝Z_w+Z_w|w||w|；d₅₅＝M_q+M_q|q||q|；d₆₆＝N_r+N_r|r||r|；X_u,X_u|u|,Y_v,Y_v|v|,Z_w，Z_w|w|,M_q,M_q|q|,N_r,N_r|r|为水动力参数；ρ,g,▽,分别为水密度、重力加速度、水容积和纵向稳心高；ω_u、ω_v、ω_w、ω_q、ω_r为外界干扰在AUV运动系各自由度的分量；

位置误差：

轨迹跟踪位置误差模型：

其中，

期望姿态：

2、定义虚拟速度误差变量：

α＝v_t sine_ψ，β＝v_p sine_θ；

步骤3中所涉及的纵向速度虚拟控制律u_d，纵倾角速度虚拟控制律q_d和艏摇角速度虚拟控制律r_d的表达式分别为：

纵向速度虚拟控制律：

u_d＝-k₁e_x/e+v_psinθ_dsinθ+v_tcosθcose_ψ，

其中，k₁为正常数，

艏向角、纵倾角速度虚拟控制律：

3、所述的纵向速度误差e_u角速，度误差e_r、e_q，生物启发模型的表达式分别为：

纵向速度误差：

e_u＝u-u_d；

角速度误差：

生物启发模型：

其中i＝u,q,r；j＝1,2,3,S_u、S_q和S_r分别为纵向速度误差、纵倾角速度误差和首向角速度误差动态模型的输出；参数A_j是正常数,为动态速度误差输出的衰减率；正常数B_j和D_j分别为动态速度误差输出的上限和下限；e_u、e_q和e_r的值通过分别设置A_j、B_j和D_j以及生物模型本身的特性来完成对速度误差的动态调节，函数f(e_i)＝max{e_i,0},g(e_i)＝max{-e_i,0}。

4、所述的纵向控制力矩τ_u的控制信号、纵倾控制力矩τ_q和艏摇控制力矩τ_r的控制信号的表达式分别为：

其中，为对当前环境扰动的估计值；

所述的界扰动自适应控制律为：

其中，c₁,c₂,c₃均是正常数。

本发明方法针对欠驱动无人水下航行器三维轨迹跟踪控制中的位置、速度、姿态等随时间变化的要求，定义了虚拟速度误差控制变量的反步控制设计方法，有别于传统定义虚拟速度误差变量的方法，有效的避免了控制律中出现奇异值的问题，并利用生物启发模型来调节所设计的速度误差，实现了对速度进行一定范围内的动态调节的目的，该设计在保证避免奇异值的同时，提高了控制器的性能。同时设计了欠驱动AUV平面动态速度调节轨迹跟踪控制器，并基于李雅普诺夫理论证明了该控制系统误差在外界常值扰动下最终一致有界。仿真研究中考虑到了艏向角误差为±90°的情况，仿真结果表明，本发明所提出的控制方法收敛、有效，可以实现欠驱动AUV三维轨迹的精确跟踪控制。

相比已有平面动态速度调节轨迹跟踪方法，本发明方法不仅将其扩展到三维空间中，而且还能针对不光滑轨迹进行精确的跟踪，对拐点以及突变轨迹有较强的跟踪能力，这些对于欠驱动水下无人航行器不仅具有科学的研究意义，而且还具有工程应用价值，其更接近实际 使用，有利于加快本发明的技术转化。

本发明方法的有益效果主要体现在：

1、定义了虚拟速度误差变量，将姿态跟踪控制转化为速度控制，简化了计算过程；

2、设计了虚拟控制律，避免了基于虚拟速度误差变量反步法设计虚拟控制量时，艏向角误差为±90°时的奇异值问题；

3、将纵向速度误差、艏向角速度误差和纵倾角速度误差分别通入到生物启发模型，完成了对速度的动态调节增加了系统的控制性能；

4、在外界常值扰动下可以实现对欠驱动AUV不光滑的三维轨迹精确跟踪控制。

附图说明

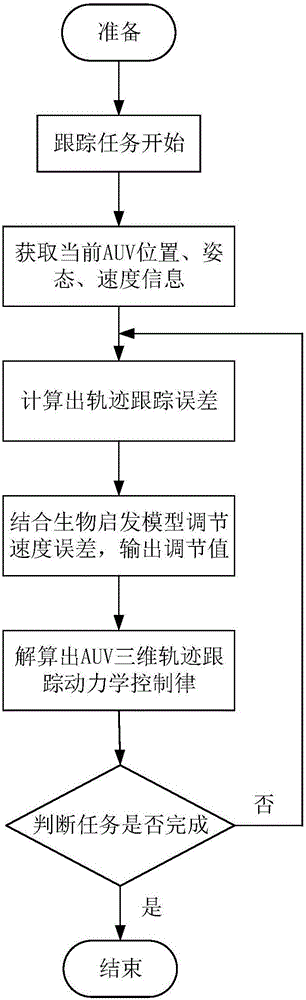
图1欠驱动水下无人航行器三维轨迹跟踪控制结算流程图；

图2 AUV大地坐标系与船体坐标系；

图3欠驱动AUV三维轨迹跟踪控制系统结构图；

图4三维轨迹跟踪控制效果图；

图5三维轨迹跟踪XY平面投影；

图6三维轨迹跟踪XZ平面投影；

图7 AUV总位置误差和姿态角误差；

图8 AUV三维轨迹跟踪位置误差；

图9 AUV线速度响应曲线；

图10 AUV角速度响应曲线；

图11 AUV实际控制输入；

图12 AUV纵向速度误差与其调节输出；

图13 AUV纵倾角速度误差与其调节输出；

图14 AUV艏向角速度误差与其调节输出。

具体实施方式

下面举例对本发明做更详细的描述。

步骤1中AUV根据当前任务，将期望轨迹位置信息给定AUV，并通过所搭载的导航设备和传感器采集数据，获得当前的位置X(t)＝[x(t),y(t),z(t)]^T信息、姿态[θ(t),ψ(t)]^T信息、速 度V(t)＝[u(t),v(t),ω(t),q(t),r(t)]^T信息。

然后AUV获取在地面坐标系下的初始位置X(t)＝[x(t),y(t),z(t)]^T，AUV初始的艏向角ψ(t)，纵倾角θ(t)，AUV的初始纵向速度u_r(t)、横向速度v_r(t)和艏摇角速度r(t)，并给定期望轨迹位置X_d(t)＝[x_d(t),y_d(t),z_d(t)]^T。

步骤2中利用步骤1中的信息，通过欠驱动AUV的数学模型和轨迹跟踪位置误差模型，计算出实际轨迹与期望轨迹之间的位置误差，和期望姿态，将地面坐标信息转换为船体坐标信息。

所涉及的欠驱动AUV的数学模型包括运动学模型和动力学模型表达式为：

运动学模型：

动力学模型：

其中：d₁₁＝X_u+X_u|u||u|；d₂₂＝Y_v+Y_v|v||v|；d₃₃＝Z_w+Z_w|w||w|；d₅₅＝M_q+M_q|q||q|；d₆₆＝N_r+N_r|r||r|；X_u,X_u|u|,Y_v,Y_v|v|,Z_w，Z_w|w|,M_q,M_q|q|,N_r,N_r|r|为水动力参数；ρ,g,▽,分别为水密度、重力加速度、水下全排水容积和初稳心高；ω_u、ω_v、ω_w、ω_q、ω_r为外界干扰在AUV运动系各自由度的分量。

根据给定的期望轨迹位置信息可以得到AUV的期望姿态：

姿态误差方程为：

所述的将地面坐标信息转换为船体坐标的过程如下：

首先根据期望轨迹获得地面坐标系下的位置误差为：

再经过坐标转换后得到新的船体坐标系下的位置误差为：

轨迹跟踪位置误差模型：

其中定义至此完成了欠驱动AUV的初始化设置。

欠驱动AUV满足如下的假设：

假设1.1欠驱动AUV的速度和控制输入均有界,即其中,均为已知的上界。

假设1.2当t＞0时,期望轨迹的变量u_d,q_d,r_d均有界,且它们的导数也有界。

假设1.3对欠驱动AUV的纵倾角|θ(t)|≤π/2。

步骤3中按下式分别给出或计算出所定义的虚拟速度误差变量、纵向速度虚拟控制律u_d、纵倾角速度虚拟控制律q_d和艏向角速度虚拟控制律r_d。

对于位置误差(6)构造李雅普诺夫能量函数：

定义虚拟速度误差变量：

α＝v_t sine_ψ，β＝v_p sine_θ (9)

所设计的虚拟控制律α_d、β_d：

纵向速度虚拟控制律：

u_d＝-k₁e_x/e+v_psinθ_dsinθ+v_tcosθcose_ψ (11)

其中k₁,k₂,k₃都是正常数,

给出误差变量分别为：

结合式(9)-(12)对(8)式求导可得出：

然后对虚拟控制量e_α、e_β构造李雅普诺夫能量函数：

所设计的艏向角和纵倾角速度虚拟控制律为：

给出误差变量为：

结合式(15)，(16)对(14)式求导可得出：

其中

步骤4中将步骤3中计算得出的纵向速度和纵倾角、艏向角角速度误差通入生物模型对其进行动态调节，可得到如下的方程：

其中(i＝u,q,r；j＝1,2,3),S_u、S_q和S_r分别为纵向速度误差、纵倾角速度误差和艏向角速度误差动态模型的输出；参数A_j是正常数,为动态速度误差输出的衰减率；正常数B_j和D_j分别为动态速度误差输出的上限和下限；从S_u、S_q和S_r的输出可以看出,e_u、e_q和e_r的值可以通过分别设置A_j、B_j和D_j以及生物模型本身的特性来完成对速度误差的动态调节,这也是本发明的最大创新之处,函数f(e_i)＝max{e_i,0},g(e_i)＝max{-e_i,0}。

步骤5中推导的欠驱动AUV三维轨迹跟踪的生物速度调节控制器，具体的计算和推到过程如下：

对于速度误差e_u、e_q和e_r，构造李雅普诺夫能量函数：

结合(17)式，对(19)式求导可得：

其中δ＝e_αv_tδ₁cos^-1θ+e_βv_pδ₂.

控制输入τ_u,τ_q,τ_r选取为：

其中，

结合(20)-(22)式，可得到：

其中为对当前环境扰动的估计值。

对于模型输出量S_u、S_q和S_r，构造李雅普诺夫能量函数：

结合(18)和(23)式，对(24)式求导可得：

其中(i＝u,q,r；j＝1,2,3)。

最终得到系统的误差方程

令B_j＝D_j(j＝1,2,3),当e_i＞0时,f(e_i)＝e_i,g(e_i)＝0,因此：

f(e_i)-g(e_i)-e_i＝0 (27)

当e_i＜0时,f(e_i)＝0,g(e_i)＝e_i,因此：

f(e_i)-g(e_i)-e_i＝0 (28)

其中(i＝u,q,r).因此B_u＝0,B_q＝0,B_r＝0。

将式(27)、(28)代入(25)得到：

由函数f(e_i)、g(e_i)定义可知f(e_i)≥0,g(e_i)≥0,另外参数A_j,B_j,D_j(j＝1,2,3)均是正常数,因此A_i≥0(i＝u,q,r).其中

对于外界干扰量，构造李雅普诺夫能量函数：

其中c₁,c₂,c₃都是正常数，对式(30)两边求导得：

根据式(31)分别设计外界常值干扰的自适应控制律为：

将式(32)代入式(31)，得：

且参数k₁,k₂,k₃,k₄,k₅,c₁,c₂,c₃均是正常数,且A_i≥0(i＝u,q,r).所以在假设1.1和假设1.2条件下δ＝e_αv_tδ₁cos^-1θ+e_βv_pδ₂存在最大值即δ有界。

定义结合式(33)有

2V₅＝||z||² (34)

再结合(30)有

其中γ＝min{k₁,k₂,k₃,k₄,A_u,A_q,A_r,c₁,c₂,c₃},由于δ有界,根据参考文献[8]中的比较原理,有:

因此:

式(37)表明,Lyapunov函数V₅被界定在(0-δ/2γ)范围内,即控制误差均是有界的,且收敛在半径为δ/2γ的邻域内,且可以通过增大增益k₁,k₂,k₃,k₄,A_u,A_q,A_r,c₁,c₂,c₃,获得较大的γ值,以使收敛半径变的足够小.即系统误差最终一致有界。

仿真实验验证与分析

下面举例说明并验证本发明方法的有效性：

为了验证所提控制方法的优点和有效性,及动态速度调节的效果,并从实际工程的角度考虑设计了一种螺旋下潜并结合平面搜索的三维时变轨迹曲线.为了证明所设计控制器能够有效的解决当艏向角误差ψ_e＝±π/2时控制律中存在奇异值的情况,在设计平面跟踪时考虑到了此种情况.其中螺旋下潜部分选取轨迹为

起始点为(x,y,z)＝(10,90,10),即选取的初始位置误差为(x_e,y_e,z_e)＝(10,-10,10),螺旋下潜与平面轨迹的切换a点选取为(x,y,z)＝(-54.4,-84.0,100),几个轨迹直角拐点分别选取为b:(x,y,z)＝(-104.4,-84.0,100),c:(x,y,z)＝(-104.4,66.0,100),d:(x,y,z)＝(-154.4,66,100),e:(x,y,z)＝(-154.4,-84.0,100),f:(x,y,z)＝(-204.4,-84.0,100)。初始姿态和航速均为零，控制增益为:k₁＝2,k₂＝0.5,k₃＝1,k₄＝0.5,c₁＝0.5,c₂＝0.1,c₃＝0.1，三个生物模型参数分别选取为：

模型参数如下:仿真中所用到的模型参数为:m＝165kg,I_z＝50kgm²,X_u＝70kg/s,X_u|u|＝100kg/s,Y_v＝100kg/m,Y_v|v|＝200kg/m,Z_w＝100kg/s,Z_w|w|＝200kg/s,N_r＝50kgm²/s,N_r|r|＝100kgm²,M_q＝50kgm²/s,M_q|q|＝100kgm²。外界常值环境扰动为:ω_u＝0.5N,ω_v＝0N,ω_w＝0N,ω_r＝0.1Nm,ω_r＝0.1Nm。Simulink仿真实验结果如图4-图14所示。

图4为欠驱动AUV对期望轨迹的三维空间螺旋与平面跟踪；

图5、图6,分别为三维轨迹跟踪XY平面投影和三维轨迹跟踪XZ平面投影，控制器在juyou一定初始位置念头下较平滑的实现对三维路径的跟踪控制，且保证了跟踪精度；

图7、图8表示出各项跟踪的误差都足够小,且最终趋于零,图7中我们定义的 表示的是期望轨和实际轨迹的总体误差值,其中五个艏向角误差ψ_e＝±π/2也清晰可见，在拐点处跳变大的问题得到解决，艏向角的超调振荡小，调节时间短，控制效果好，说明本发明所提控制方法的有效性和鲁棒性；从图8可以看出各项位置误差的变化,且较快的趋于零；

图9为欠驱动AUV线速度响应曲线,从中可以看出即使在角度突变的情况下,速度变化依然较缓,说明所提方法很好的抑制了速度突变的问题；

图10为欠驱动AUV角速度响应曲线,虽然在角度突变时有较大的变化,但依然能实现对跟踪误差的控制；

图11为AUV的实际控制输入相应的变化情况；

图12、图13、图14分别为纵向速度误差、纵倾角速度误差、艏向角速度误差分别与其通入生物启发模型后的输出,可以看出其动态速度调节的效果很明显,图12中纵向速度误差在拐点突变出缩小超调约25％；图13中纵倾角速度误差在螺旋曲线向平面过度时缩小超调约28％；图14艏向角速度误差在每个拐点处缩小超调最大约26％；调节后的各项速度误差输出明显小于调节前；

从图4-图14可以看出本发明所设计的欠驱动AUV生物速度调节轨迹跟踪控制器能够实现在外界常值扰动下对时变三维轨迹的精确跟踪。