一种无人机飞行控制系统的故障可分离性评价方法与流程

本发明涉及一种无人机飞行控制系统的故障可分离性评价方法，用于评价无人机飞行控制系统中执行器故障和传感器故障实现故障分离的难易程度，属于无人机系统故障分离
技术领域：
。
背景技术：
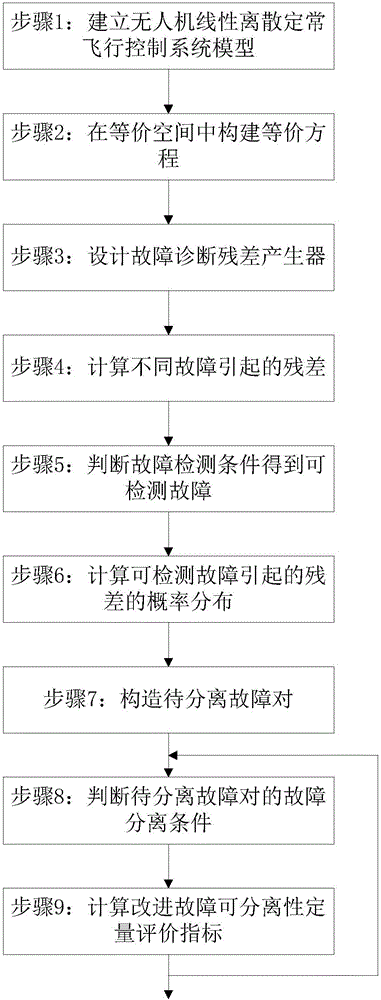
：无人机在现代侦察、工程测绘和科学实验等领域得到广泛应用，具有较为可观的军用与民用前景。无人机飞行控制系统是无人机实现自主飞行或半自主飞行的控制系统，对稳定和控制无人机姿态、管理无人机完成任务起到至关重要的作用。无人机在飞行过程中易受复杂环境因素的影响，飞行控制系统不可避免会发生故障，易导致无人机难以完成任务，甚至造成无人机坠毁事故。目前对无人机飞行控制系统故障检测的研究已取得大量成果，但无人机飞行控制系统故障分离算法的设计以及故障可分离性分析尚待进一步研究。一方面，在无人机飞行控制系统的设计阶段若不考虑故障可分离性，易导致设计的无人机飞行控制系统难以实现故障分离，系统发生故障时无法及时修复故障；另一方面，无人机飞行控制系统中执行器故障和传感器故障缺乏统一的故障可分离性定量指标，难以定量评价不同故障分离的难易程度，因此对无人机故障可分离性评价的研究至关重要。目前，对于系统故障分离难易程度的评价问题，大多数研究成果根据控制输入与量测输出的冗余关系定性评价故障可分离性。王振西等所撰论文“基于系统冗余关系的可诊断性方法研究[J].航天控制,2013,31(6):10-16,26”利用故障变量能否引起输出变量变化构造关联矩阵，利用关联矩阵分析故障可分离性，但该方法仅能定性判断系统中不同故障能否分离，不能定量评价故障分离的难易程度，且未能考虑未知输入对故障分离的影响。王大轶等所撰专利“一种噪声影响下航天器控制系统可诊断性确定方法[P].中国,201410827895.6”利用等价空间方法产生故障诊断残差，将故障可分离性的评价问题转化为残差向量距离相似度判别问题或方向相似度判别问题，但该方法仅能定量评价残差在距离或方向上的差异，未能综合评价残差向量在距离和方向上的差异。总之，现有故障可分离性评价方法仅能定量评价不同故障引起的残差向量在距离上的差异或方向上的差异，尚未有文献或专利提出的故障可分离性评价方法能够综合评价残差向量在距离和方向上的差异并将定性方法和定量方法相结合，故障可分离性评价方法有待深入研究。技术实现要素：本发明的技术解决问题是：评价无人机飞行控制系统故障分离的难易程度，利用等价空间中不同故障引起的故障诊断残差向量的余弦距离建立故障分离条件；利用残差向量的相似度定量评价故障分离的难易程度，将模式识别中距离相似度和方向相似度相结合，提出一种改进故障可分离性定量评价指标，利用故障分离条件和故障可分离性定量评价指标评价故障可分离性。本发明的技术解决方案为：一种无人机飞行控制系统的故障可分离性评价方法，包括下列步骤：步骤1：根据无人机飞行控制系统原理，建立无人机线性离散定常飞行控制系统模型如下：x(k+1)=Ax(k)+Bu(k)+Bdd(k)+Bff(k)y(k)=Cx(k)+Du(k)+Ddd(k)+Dff(k)]]>其中，分别为状态变量、控制输入变量、输出变量、未知输入变量和故障变量，根据无人机飞行控制系统结构和飞行环境确定；nx、nu、ny、nd、nf分别为x(k)、u(k)、y(k)、d(k)、f(k)的维数，k表示采样时刻，分别表示所有nx、nu、ny、nd、nf维实数向量；d(k)包括噪声、大气扰动以及模型不确定性，假设无人机飞行控制系统中未知输入变量为线性互不相关的零均值高斯随机向量表示均值为0、协方差矩阵为Λd的高斯随机分布，0表示零矩阵或零向量，Λd为d的协方差矩阵；无人机飞行控制系统中故障变量f为l2范数有界的确定性加性故障，且fi(k),1≤i≤nf为故障变量f(k)的第i个分量，fi(k)≠0表示某执行器或传感器发生故障；A、B、C、D分别为无人机飞行控制系统的系统矩阵、输入矩阵、输出矩阵和传输矩阵，根据无人机飞行控制系统的结构和参数确定；Bf、Df为根据系统故障f类型确定的已知矩阵或向量，Bd、Dd为根据系统未知输入d类型确定的已知矩阵或向量；步骤2：根据无人机飞行控制系统结构、参数和计算能力，确定等价空间阶数表示所有正整数，由步骤1所述的无人机线性离散定常飞行控制系统控制输入变量u(k)和输出变量y(k)的冗余关系，在等价空间中构建无人机飞行控制系统的等价方程；步骤3：对步骤2所述的无人机飞行控制系统的等价空间中等价方程进行等价变换，根据未知输入d和无人机飞行控制系统参数设计无人机飞行控制系统故障诊断残差产生器；步骤4：根据步骤3所述的无人机飞行控制系统故障诊断残差产生器计算未知输入d引起的残差向量rd和不同故障fi引起的标称残差向量rfi,1≤i≤nf，根据rd、rfi计算不同故障fi引起的残差向量ri,1≤i≤nf；步骤5：根据步骤4所述的不同故障引起的标称残差向量rfi，建立故障fi的故障检测条件，依次判断各故障能否满足故障检测条件，得到无人机飞行控制系统中可检测故障表示无人机飞行控制系统的可检测故障数；步骤6：根据步骤3所述的无人机飞行控制系统故障诊断残差产生器和等价空间中未知输入变量ds的概率分布，计算未知输入d引起的残差向量rd的概率分布，根据rd的概率分布计算步骤5所述的无人机飞行控制系统可检测故障引起的残差向量的概率分布；步骤7：若无人机飞行控制系统中故障均不可检测或可检测故障数则系统中不含待分离故障对；若可检测故障数将无人机飞行控制系统中任意两个可检测故障构造待分离故障对；步骤8：从第一组待分离故障对开始，根据步骤7所述的待分离故障对中故障引起的残差向量和标称残差向量的方向差异，依次建立待分离故障对的故障分离条件，判断待分离故障对能否满足故障分离条件；步骤9：若待分离故障对满足步骤8所述的故障分离条件，计算待分离故障对的改进故障可分离性定量评价指标判断是否全部待分离故障对分析完毕，若是，则故障可分离性定量评价结束，否则回到步骤8继续计算，直至全部待分离故障对故障可分离性评价完毕。其中，步骤2中所述的无人机飞行控制系统在等价空间中的等价方程的具体求解方法为：首先，根据等价空间阶数s，在等价空间中构建无人机飞行控制系统的等价方程如下：ys(k)-Husus(k)＝Hosx(k-s)+Hdsds(k)+Hfsfs(k)其中，ys(k)、us(k)、ds(k)、fs(k)分别表示y(k)、u(k)、d(k)、f(k)在等价空间中的输出变量、控制输入变量、未知输入变量和故障变量；分别表示所有(ny·(s+1))×(nu·(s+1))、(ny·(s+1))×(nd·(s+1))、(ny·(s+1))×(nf·(s+1))、(ny·(s+1))×nx维实数矩阵，分别表示所有nu·(s+1)、nd·(s+1)、nf·(s+1)、ny·(s+1)维实数向量。其中，步骤3所述的无人机飞行控制系统故障诊断残差产生器的具体设计方法为：首先对无人机飞行控制系统的等价方程进行等价变换，在等价方程等式两端左乘矩阵Hos的左零矩阵Ns，即NsHos＝0，得到不含状态变量x(k-s)的等价方程：Ns(ys(k)-Husus(k))＝NsHdsds(k)+NsHfsfs(k)然后，计算NosHdsds的协方差矩阵Λds表示等价空间中ds的协方差矩阵，并计算P＝(Λnds)-1/2，在上述等价方程两端左乘矩阵P以满足I表示单位矩阵，得到等价方程：PNs(ys(k)-Husus(k))＝PNsHdsds(k)+PNsHfsfs(k)最后，设计无人机飞行控制系统故障诊断残差产生器为：r(k)＝NosHdsds(k)+NosHfsfs(k)其中，Nos＝PNs，无人机飞行控制系统故障诊断残差r(k)＝Nos(ys(k)-Husus(k))。其中，步骤4所述的不同故障引起的残差向量的具体求解方法为：根据无人机飞行控制系统故障诊断残差产生器r(k)，首先计算故障未发生f(k)＝0时未知输入d(k)引起的残差向量rd(k)＝NosHdsds(k)和不同故障fi(k)发生时引起的标称残差向量rfi(k)＝NosFifsi(k),1≤i≤nf，然后计算不同故障fi(k)引起的残差向量，得：ri(k)＝NosFifsi(k)+NosHdsds(k),1≤i≤nf其中，Bf,i、Df,i,1≤i≤nf分别表示Bf的第i列、Df的第i列。其中，步骤5所述的故障检测条件并得到可检测故障的具体判断方法为：当故障fi发生时，即fi(k)≠0，fi(k)引起的标称残差向量rfi(k)＝NosFifsi(k)＝0表示故障fi的发生不能引起标称残差向量rfi变化，因此故障fi不能通过残差ri被检测，fi不满足故障检测条件；当fi(k)≠0时，若rfi(k)≠0则故障fi的发生可通过残差ri被检测，fi满足故障检测条件；依次对判断故障检测条件，得到无人机飞行控制系统中可检测故障表示无人机飞行控制系统的可检测故障数。其中，步骤6所述的不同残差向量概率分布的具体求解方法为：首先，计算未知输入d引起的残差向量rd的概率分布；由于且未知输入d引起的残差向量rd相当于对未知输入变量ds进行线性变换，得到未知输入d引起的残差向量rd的概率分布为然后，计算可检测故障引起的残差向量的概率分布；由于引起的残差向量为标称残差向量为其中得到可检测故障引起的残差向量的概率分布如下：其中，分别表示Bf的第列、Df的第列。其中，步骤7所述的待分离故障对的具体求解方法为：若无人机飞行控制系统中所有故障均不可检测，即所有故障均不能实现故障分离；若无人机飞行控制系统中只有一个可检测故障，即则该故障发生时与其他故障分离问题转化为该故障的故障检测问题，此时研究故障可分离性毫无意义，因此或时无人机飞行控制系统中不含待分离故障对。若无人机飞行控制系统中可检测故障数将任意两个可检测故障构成待分离故障对，共得到组待分离故障对。其中，步骤8所述的待分离故障对故障分离条件的具体判断方法为：首先，建立可检测故障发生时与可检测故障实现故障分离条件的余弦形式；由于可检测故障发生时与可检测故障实现故障分离的条件为引起的残差向量与引起的标称残差向量间的夹角应小于与引起的标称残差向量其余弦形式为：|ri‾T·rfi‾|||ri‾||2·||rfi‾||2>|ri‾T·rfj‾|||ri‾||2·||rfj‾||2,1≤i‾≠j‾≤n‾f]]>其中，表示的欧式范数，以此类推；然后，将基于引起的标称残差向量的欧式范数建立发生时与可检测故障实现故障分离的条件化简，得：||rfi‾||2=||NosFi‾(||fsi‾||2·fsi‾,1)||2=||fsi‾||2·||rfi‾,1||2>rdT·nij‾(1-|ni‾T·nj‾|)]]>其中，最后，根据无人机飞行控制系统的实际需求确定故障分离置信度α，由于建立可分离故障fi发生时以置信度α与可检测故障分离的条件如下：||fsi‾||2>fij‾,i‾c,1≤i‾≠j‾≤n‾f]]>其中：待分离故障对中的故障分离阈值为置信度α对应的标准高斯分布置信区间上限；从第一组待分离故障对开始，判断组待分离故障对能否满足故障分离条件。其中，步骤9所述的待分离故障对的改进故障可分离性定量评价指标的具体求解方法为：首先，计算待分离故障对引起的残差向量的K-L散度改进指标该指标定量评价残差的距离相似度，即：D1(ri‾,rj‾)=max(KL(ri‾:rd),KL(rj‾:rd))min(KL(ri‾:rd),KL(rj‾:rd))]]>其中，表示rd的K-L散度(Kullback-Leiblerdivergence)，由于经计算分别表示中的最大值、最小值。由于得有意义；然后，计算待分离故障对引起的标称残差向量的正弦值该指标通过的方向差异定量评价残差的方向相似度，即：D2(ri‾,rj‾)=sin2(rfi‾,rfj‾)=1-(rfi‾T·rfj‾||rfi‾||2·||rfj‾||2)2]]>此外，考虑未知输入对故障分离的影响，引入故障可检测性定量评价指标定量评价故障与未知输入引起残差相对变化程度的差异，即：D3(ri‾,rj‾)=min(||rfi‾||2,||rfj‾||2)Jth]]>其中：表示中的最小值，定量评价故障对残差的影响程度；故障检测阈值由置信度α及残差方差确定，表示置信度为α自由度为η的卡方分布，η为Nos的行数，定量评价未知输入对残差的影响程度；最后，计算待分离故障对的改进故障可分离性定量评价指标：Di‾,j‾=D1(ri‾,rj‾)·D2(ri‾,rj‾)·D3(ri‾,rj‾)=(1-(rfi‾·rfj‾)2||rfi‾||22·||rfj‾||22)·max(||rfj‾||22,||rfj‾||22)min(||rfi‾||22,||rfj‾||22)·χα2(η),1≤i‾≠j‾≤n‾f]]>判断组待分离故障对的故障可分离性评价是否分析完毕，若是，则故障可分离性评价结束，否则回到步骤8继续计算，直至全部待分离故障对故障可分离性评价完毕。本发明与现有技术相比的优点在于：(1)本发明根据等价空间中不同故障引起的故障诊断残差向量的方向差异建立故障分离条件，将故障分离条件转化为等价空间中不同故障向量的欧式范数与故障分离阈值的比较问题，该方法直接利用故障向量欧式范数判断故障分离条件，能够更为直观地评价无人机飞行控制系统中执行器故障和传感器故障能否实现故障分离。(2)本发明利用不同故障引起的故障诊断残差向量的相似度定量评价故障可分离性，提出的改进故障可分离性定量评价指标将距离相似度和方向相似度相结合，能够更为准确地定量评价不同故障引起的残差向量在距离和方向上的差异，提高了故障可分离性评价的准确性，其故障可分离性评价结果为无人机飞行控制系统设计及故障分离算法设计提供一种参考依据。(3)本发明将故障可分离性定性评价方法和定量评价方法相结合，较比现有故障可分离性评价方法能够更为全面、准确地评价无人机飞行控制系统故障分离的难易程度。附图说明图1为无人机飞行控制系统框图；图2为本发明提出的无人机飞行控制系统的故障可分离性评价方法流程图；图3为无人机飞行控制系统故障检测图；图4为无人机飞行控制系统故障分离图。具体实施方式本发明无人机飞行控制系统框图如图1所示，主要由控制器、执行器、无人机机体和传感器组成，控制指令通过控制器作用于执行器，通过控制输入引起无人机机体位置、速度和姿态等状态变量的变化，经过传感器进行量测并将量测变量反馈给控制器，控制器再根据控制指令和量测变量产生控制输入。无人机飞行控制系统的故障可分离性评价方法流程图如图2所示，具体方法如下：步骤1：根据无人机飞行控制系统原理，建立无人机线性离散定常飞行控制系统模型如下：x(k+1)=Ax(k)+Bu(k)+Bdd(k)+Bff(k)y(k)=α(k)+Du(k)+Ddd(k)+Dff(k)]]>其中，分别为状态变量、控制输入变量、输出变量、未知输入变量和故障变量，根据无人机飞行控制系统结构和飞行环境确定；nx、nu、ny、nd、nf分别为x(k)、u(k)、y(k)、d(k)、f(k)的维数，k表示采样时刻，分别表示所有nx、nu、ny、nd、nf维实数向量；d(k)包括噪声、大气扰动以及模型不确定性，假设无人机飞行控制系统中未知输入变量为线性互不相关的零均值高斯随机向量表示均值为0、协方差矩阵为Λd的高斯随机分布，0表示零矩阵或零向量，Λd为d的协方差矩阵；无人机飞行控制系统中故障变量f为l2范数有界的确定性加性故障，且fi(k),1≤i≤nf为故障变量f(k)的第i个分量，fi(k)≠0表示某执行器或传感器发生故障；A、B、C、D分别为无人机飞行控制系统的系统矩阵、输入矩阵、输出矩阵和传输矩阵，根据无人机飞行控制系统的结构和参数确定；Bf、Df为根据系统故障f类型确定的已知矩阵或向量，Bd、Dd为根据系统未知输入d类型确定的已知矩阵或向量；步骤2：根据无人机飞行控制系统结构、参数和计算能力，确定等价空间阶数表示所有正整数，由步骤1所述的无人机线性离散定常飞行控制系统控制输入变量u(k)和输出变量y(k)的冗余关系，在等价空间中构建无人机飞行控制系统的等价方程如下：ys(k)-Husus(k)＝Hosx(k-s)+Hdsds(k)+Hfsfs(k)其中，ys(k)、us(k)、ds(k)、fs(k)分别表示y(k)、u(k)、d(k)、f(k)在等价空间中的输出变量、控制输入变量、未知输入变量和故障变量；分别表示所有(ny·(s+1))×(nu·(s+1))、(ny·(s+1))×(nd·(s+1))、(ny·(s+1))×(nf·(s+1))、(ny·(s+1))×nx维实数矩阵，分别表示所有nu·(s+1)、nd·(s+1)、nf·(s+1)、ny·(s+1)维实数向量。步骤3：根据步骤2所述的无人机飞行控制系统等价空间中等价方程设计无人机飞行控制系统故障诊断残差产生器。首先对步骤2所述的无人机飞行控制系统的等价空间中在等价方程等式两端左乘矩阵Hos的左零矩阵Ns，即NsHos＝0，得到不含状态变量x(k-s)的等价方程：Ns(ys(k)-Husus(k))＝NsHdsds(k)+NsHfsfs(k)，然后计算NosHdsds(k)的协方差矩阵Λds表示等价空间中ds的协方差矩阵，并计算P＝(Λnds)-1/2，此时I表示单位矩阵，得到等价方程：PNs(ys(k)-Husus(k))＝PNsHdsds(k)+PNsHfsfs(k)，最后设计无人机飞行控制系统故障诊断残差产生器：r(k)＝NosHdsds(k)+NosHfsfs(k)其中，Nos＝PNs，无人机飞行控制系统故障诊断残差r(k)＝Nos(ys(k)-Husus(k))。步骤4：根据步骤3所述的无人机飞行控制系统故障诊断残差产生器计算不同故障引起的残差。首先计算故障未发生f(k)＝0时未知输入d(k)引起的残差向量rd(k)＝NosHdsds(k)和不同故障fi发生时引起的标称残差向量rfi(k)＝NosFifsi(k),1≤i≤nf，然后计算不同故障fi引起的残差向量为：ri(k)＝NosFifsi(k)+NosHdsds(k),1≤i≤nf其中，Bf,i、Df,i,1≤i≤nf分别表示Bf的第i列、Df的第i列。步骤5：根据步骤4所述的不同故障引起的标称残差向量rfi判断故障检测条件。当故障fi发生时，即fi(k)≠0，fi引起的标称残差向量rfi(k)＝NosFifsi(k)＝0则故障fi的发生不能引起标称残差向量rfi变化，因此故障fi不能通过残差ri被检测，fi不满足故障检测条件；当fi(k)≠0时，若rfi(k)≠0则故障fi的发生可通过残差ri被检测，fi满足故障检测条件。依次对判断故障检测条件，得到无人机飞行控制系统中可检测故障表示无人机飞行控制系统的可检测故障数。步骤6：根据无人机飞行控制系统故障诊断残差产生器和未知输入的概率分布，计算无人机飞行控制系统可检测故障引起的残差的概率分布。首先，计算未知输入d引起的残差向量rd的概率分布。由于且未知输入d引起的残差向量rd相当于对未知输入变量ds进行线性变换，得到未知输入d引起的残差向量rd的概率分布为然后，计算可检测故障引起的残差向量的概率分布。由于引起的残差向量为标称残差向量为其中得到可检测故障引起的残差向量的概率分布如下：其中，分别表示Bf的第列、Df的第列。步骤7：根据无人机飞行控制系统的可检测故障构造无人机飞行控制系统的待分离故障对。若无人机飞行控制系统中所有故障均不可检测，即所有故障均不能实现故障分离；若无人机飞行控制系统中只有一个可检测故障，即则该故障发生时与其他故障分离问题转化为该故障的故障检测问题，此时研究故障可分离性毫无意义，因此或时无人机飞行控制系统中不含待分离故障对。若无人机飞行控制系统中可检测故障数将任意两个可检测故障构成待分离故障对，共得到组待分离故障对。步骤8：依次建立待分离故障对的故障分离条件，判断无人机飞行控制系统待分离故障对能否满足故障分离条件。首先，建立可检测故障发生时与可检测故障实现故障分离条件的余弦形式。由于可检测故障发生时与可检测故障实现故障分离的条件为引起的残差向量与引起的标称残差向量间的夹角应小于与引起的标称残差向量其余弦形式为：|ri‾T·rfi‾|||ri‾||2·||rfi‾||2>|ri‾T·rfj‾|||ri‾||2·||rfj‾||2]]>其中，表示的欧式范数，以此类推。然后，将基于引起的标称残差向量的欧式范数建立发生时与可检测故障实现故障分离的条件化简，得：||rfi‾||2=||NosFi‾(||fsi‾||2·fsi‾,1)||2=||fsi‾||2·||rfi‾,1||2>rdT·nij‾(1-|ni‾T·nj‾|)]]>其中，最后，根据无人机飞行控制系统的实际需求确定故障分离置信度α，由于建立可分离故障发生时以置信度α与可检测故障分离的条件如下：||fsi‾||2>fij‾,ic‾,1≤i‾≠j‾≤n‾f]]>其中：待分离故障对中的故障分离阈值为置信度α对应的标准高斯分布置信区间上限。从第一组待分离故障对开始，判断组待分离故障对能否满足故障分离条件。步骤9：若待分离故障对满足步骤8所述的故障分离条件，计算待分离故障对的改进故障可分离性定量评价指标。首先，计算待分离故障对引起的残差向量的K-L散度改进指标该指标定量评价残差的距离相似度，即：D1(ri‾,rj‾)=max(KL(ri‾:rd),KL(rj‾:rd))min(KL(ri‾:rd),KL(rj‾:rd))]]>其中，表示rd的K-L散度(Kullback-Leiblerdivergence)，由于经计算分别表示中的最大值、最小值。由于得有意义。然后，计算待分离故障对引起的标称残差向量的正弦值该指标通过的方向差异定量评价残差的方向相似度，即：D2(ri‾,rj‾)=sin2(rfi‾,rfj‾)=1-(rfi‾T·rfj‾||rfi‾||2·||rfj‾||2)2]]>此外，考虑未知输入对故障分离的影响，引入故障可检测性定量评价指标定量评价故障与未知输入引起残差相对变化程度的差异，即：D3(ri‾,rj‾)=min(||rfi‾||2,||rfj‾||2)Jth]]>其中：表示中的最小值，定量评价故障对残差的影响程度；故障检测阈值由置信度α及残差方差确定，表示置信度为α自由度为η的卡方分布，η为Nos的行数，定量评价未知输入对残差的影响程度。最后，计算待分离故障对的改进故障可分离性定量评价指标：Di‾,j‾=D1(ri‾,rj‾)·D2(ri‾,rj‾)·D3(ri‾,rj‾)=(1-(rfi‾·rfj‾)2||rfi‾||22·||rfj‾||22)·max(||rfj‾||22,||rfj‾||22)min(||rfi‾||22,||rfj‾||22)·χα2(η),1≤i‾≠j‾≤n‾f]]>判断组待分离故障对的故障可分离性评价是否分析完毕，若是，则故障可分离性评价结束，否则回到步骤8继续计算，直至全部待分离故障对故障可分离性评价完毕。本发明以一种固定翼无人机在H0＝7000m，V0＝0.4Ma的等速无侧滑平直飞行状态下的纵向模型为例评价故障可分离性。步骤1：取系统状态变量x(t)＝[VαqθH]T，控制输入量u(t)＝[δeδp]T，量测变量y(t)＝[VqθH]T，f(t)表示执行器故障或传感器故障，其中本实施例中执行器故障以升降舵恒偏差故障f1＝0.5为例，传感器故障以俯仰陀螺恒偏差故障f2＝0.5、垂直陀螺恒偏差故障f3＝0.5为例，故障向量f＝[f1f2f3]T，假设未知输入其中d1,d2,d3分别为过程噪声，大气干扰及量测噪声，其中大气干扰d2中考虑水平风速和垂直风速，忽略侧向风速，建立无人机线性连续定常飞行控制系统模型如下：x·(t)=Acx(t)+Bcu(t)+Bfcf(t)+Bdcd2(t)+d1(t)y(t)=Ccx(t)+Dfcf(t)+d3(t)]]>其中：在Matlab仿真环境下，令采样时间T＝0.01s，利用Matlab离散化工具，建立无人机线性离散定常飞行控制系统模型如下：x(k+1)=Ax(k)+Bu(k)+Bff(k)+Bdd2(k)+d1(k)y(k)=Cx(k)+Dff(k)+d3(k)]]>其中：步骤2：根据无人机飞行控制系统状态维数nx＝5，设定等价空间阶数s＝5，置信度α＝0.05，建立等价空间中等价方程如下：ys(k)-Husus(k)＝Hosx(k-s)+Hdsds(k)+Hfsfs(k)其中，us(k)＝[uT(k-5)uT(k-4)…uT(k)]T，ys(k)、ds(k)、fs(k)以此类推；Hus、Hds以此类推。步骤3：首先计算Hos的左零矩阵在等价方程等式两端左乘矩阵Hos，得：Ns(ys(k)-Husus(k))＝NsHdsds(k)+NsHfsfs(k)然后，计算NosHdsds(k)的协方差矩阵并计算得到等价方程：PNs(ys(k)-Husus(k))＝PNsHdsds(k)+PNsHfsfs(k)最后，设计无人机飞行控制系统故障诊断残差产生器为：r(k)＝NosHdsds(k)+NosHfsfs(k)其中，步骤4：根据步骤3所述的无人机飞行控制系统故障诊断残差产生器r(k)，得到rd(k)＝NosHdsds(k)、不同故障fi发生时引起的标称残差向量rfi(k)＝NosFifsi(k)(i＝1,2,3)以及不同故障fi发生时引起的残差向量ri(k)＝NosFifsi(k)+NosHdsds(k)(i＝1,2,3)，其中F2、F3以此类推。步骤5：根据步骤4所述的不同故障引起的标称残差向量rfi，由于fi(k)≠0(i＝1,2,3)时，得f1满足故障分离条件，同理可得f2、f3满足故障分离条件，f1、f2、f3均为可检测故障。步骤6：计算引起残差的的概率分布为步骤7：由于无人机飞行控制系统中可检测故障数将任意两个可检测故障构成待分离故障对，共得到3组待分离故障对。步骤8：根据引起的标称残差向量的欧式范数，建立f1发生时与f2分离的条件如下：||rf1||2=||fs1||2·||rf1,1||2>rdT·n12(1-|n1T·n2|)]]>其中，fs1,1＝0.4082×[111111]T，根据置信度0.05，由于得ρ12＝1.96，建立可分离故障f1发生时以置信度0.05与可检测故障f2分离的条件为||fs1||2＞f12,1c＝0.7305。由于||fs1||2＝1.2247＞0.7305，f1发生时能以置信度0.05与可检测故障f2分离，其余故障分离以此类推，得到故障分离阈值如表1所示，其中故障f1发生时不能以置信度0.05与可检测故障f3分离，其余情况均能实现故障分离。表1无人机纵向控制系统故障分离阈值步骤9：首先，计算待分离故障对f1、f2引起的残差向量r1、r2的K-L散度改进指标：然后计算待分离故障对f1、f2引起的标称残差向量rf1、rf2的正弦值D2(r1,r2)＝sin2(rf1,rf2)＝0.9962；置信度0.05下故障检测阈值Jth＝30.14，计算故障可检测性定量评价指标：得到待分离故障对f1、f2的改进故障可分离性定量评价指标D1,2＝246.8，其它待分离故障对的改进故障可分离性定量评价指标以此类推，得到改进故障可分离性定量评价指标如表2所示。表2无人机纵向控制系统改进故障可分离性定量评价指标由表2可知，待分离故障对f1、f3的改进故障可分离性定量评价指标D1,3远低于其它待分离故障对的改进故障可分离性定量评价指标，与表1结果相符。为了验证本发明的分析结果，首先对上述无人机飞行控制系统进行故障检测，仿真5s数据，在2s依次加入f1、f2、f3，其故障检测残差评价函数分别为Jk1、Jk2、Jk3；置信度0.05下故障检测阈值为表示置信度为0.05、自由度为19的卡方分布，得到无人机飞行控制系统故障检测图如图3所示。由于图3中故障f1、f2、f3发生后故障检测残差评价函数Jk1、Jk2、Jk3均明显高于故障检测阈值Jth，说明故障f1、f2、f3均可检测。本发明利用方向性残差进行故障分离验证本评价方法的正确性，依次计算待分离残差ri与标称残差rf1、rf2、rf3的余弦距离，由于余弦距离最大的标称残差与ri方向最相近，由该标称残差的故障类型确定系统发生的故障类型。记故障fi引起的ri与fj的标称残差向量rfj的余弦距离为Jij，无人机飞行控制系统故障分离图如图4所示，其中故障f1发生时J11、J12、J13如图4a所示；故障f2发生时J21、J22、J23如图4b所示；故障f3发生时J31、J32、J33如图4c所示，图4c中第二张图为第一张图的局部放大图。由图4a可知，f1发生时，故障f1引起的残差向量r1与故障f1的标称残差向量rf1的余弦距离J11明显大于r1与故障f2的标称残差向量rf2的余弦距离J12，说明故障f1发生时残差向量r1与rf1的夹角明显小于r1与rf2的夹角，f1发生时易于与f2实现故障分离；但r1与rf1的余弦距离J11同r1与rf3的余弦距离J13没有明显区别，说明故障f1发生时r1与rf1的夹角同r1与rf3的夹角没有明显区别，f1发生时难以与f3实现故障分离，与本发明评价方法相符。由图4b可知，f2发生时，r2与rf2的余弦距离J22明显大于r2与rf1、rf3的余弦距离J21、J23，说明故障f2发生时r2与rf2的夹角明显小于r2与rf1、rf3的夹角，f2发生时易于与f1、f3实现故障分离，与本发明所述评价方法相符。由图4c可知，f3发生时，r3与rf3的余弦距离J33略大于r3与rf1的余弦距离J31，说明r3与rf3的夹角略小于r3与rf1的夹角，f3发生时能与f1实现故障分离；r3与rf3的余弦距离J33明显大于r3与rf2的余弦距离J32，说明r3与rf3的夹角明显小于r3与rf2的夹角，f3发生时易于与f2实现故障分离，与本发明评价方法相符，验证了本发明的有效性。当前第1页1 2 3