基于遗传算法和MMAS算法的塔机群多任务的调度方法与流程
本发明涉及塔机控制领域,特别涉及一种基于遗传算法和MMAS算法的塔机群多任务的调度方法。
背景技术:
塔机是建设房屋和桥梁的主要运输作业工具。随着建筑作业的密集化发展,多台塔机作业区域的相互覆盖为塔机带来严重安全隐患的同时也为塔机群协同作业带来了可能,利用多台塔机“合作运输”的方式,我们可以将建筑物料运送到更远的地方。然而现有技术中如何利用“合作运输”为各塔机制定完善的作业方案还未解决,不仅能够避免危险情况的产生,还能提升塔机群的作业效率。同时,塔机群在多任务环境下的作业情况值得被考虑,针对某单一任务的执行效率提升方案极有可能对相关另一任务的执行情况产生负面影响。
技术实现要素:
本发明提供一种基于遗传算法和MMAS算法的塔机群多任务的调度方法,解决了现有技术中如何使多台塔机合作运输的技术问题,达到了提供一种为塔机制定完善方案、合作运输的塔机调度方法的技术效果。
为解决上述技术问题,本发明提供一种基于遗传算法和MMAS算法的塔机群多任务的调度方法,所述塔机群具有交叉区域,所述调度方法包括:
步骤一,基于遗传算法,获取初始种群;随机在所述塔机群各任务选择D条调度路径作为遗传算法的初始种群,所述塔机群记为{T1,T2,……,Tn},Tn为第n个塔机;
步骤二,基于MMAS算法,获取初始路径;在所述塔机群各任务的交叉区域内,为所述选择的D条调度路径选择装卸点作为MMAS算法的初始路径;
步骤三,根据步骤一和步骤二中选择的遗传算法的初始种群和MMAS算法的初始路径,分解塔机群多任务路径为多次双塔机作业,计算所述多次双塔机作业所需的时间,最后一个塔机作业的完成时间为该调度方案总耗时;其中所述计算所述多次双塔机作业所需的时间具体为多次双塔机每条调度路径独立完成所需的时间;
步骤四,将所述调度方案总耗时作为更新MMAS算法中的信息素,返回步骤二开始迭代寻找基于已定调度路径下使该调度方案总耗时最短的最优交接点,所述最优交接点为基于MMAS算法迭代至第一预设次数终止时调度方案总耗时最短的所述D条调度路径的装卸点;
步骤五,基于遗传算法,将步骤四中得到最短的调度方案总耗时作为参考保留优质种群,淘汰劣质种群,优质种群之间相互交叉生成新的种群以保证种群数量;返回步骤二开始迭代寻找最优种群,所述最优种群为基于遗传算法迭代至第二预设次数终止时最优种群为最优调度方案。
优选的,在所述步骤四之前,所述步骤三之后,所述调度方法还包括:
当所述塔机群为多作业并行情况时,基于防碰撞算法对塔机作业完成的时间以延迟等待的方式进行修正,获取最后一个塔机作业的完成时间为该调度方案总耗时。
优选的,所述步骤三中所述分解塔机群多任务路径为多次双塔机作业,计算所述多次双塔机作业所需的时间,最后一个塔机作业的完成时间为该调度方案总耗时,所述调度方案总耗时具体为:
Tj1=TX1+TX2+……+TXn-1+TN;
其中,Tj1为任务J1的调度方案总耗时,X1,X2,……,Xn-1为任务J1的调度方案的n-1个装卸点,TX1、TX2、……、TXn-1、TN分别为X1,X2,……,Xn-1的n段路径的耗时。
优选的,所述步骤三中所述分解塔机群多任务路径为多次双塔机作业,具体为:
所述塔机群多任务路径为Tnum111→Tnum12,num222→……→Tnum1n,num2nn;
将塔机群多任务路径分解为{(Tnum111→Tnum122),(Tnum222→Tnum133),……,(Tnum1n-1n-1→Tnum1nn),Tnum2nn};
其中,Tnum1n,num2nn为第n个塔机,且第n个塔机的吊臂具有两个旋转方向{num1n,num2n},cw表示顺时针旋转,aw表示逆时针旋转,其中num1n和num2n均可以取cw和aw两个值。
优选的,所述步骤三中所述计算所述多次双塔机作业所需的时间中,每次双塔机作业所需的时间,具体计算方法为:
通过计算确定双塔机吊臂合适的旋转方向以获得最小调度时长时所需的时间。
优选的,所述步骤三中所述计算所述多次双塔机作业所需的时间中,每次双塔机作业所需的时间,具体计算方法为:
当双塔机作业为高塔到低塔作业时,货物由塔机T1交于T2,且T1高于T2,塔机T1和塔机T2具有一交叉区域Q,X为交叉区域S中的装卸点,双塔机作业所需的时间取决于塔机吊臂旋转时间、变幅小车移动时间和吊钩起升/下放时间中的最大值。
优选的,所述当双塔机作业为高塔到低塔作业时,货物由塔机T1交于T2,且T1高于T2时,塔机T1和塔机T2具有一交叉区域Q,X为交叉区域S中的装卸点,双塔机作业所需的时间,具体计算方法为:
当塔机T1的吊臂旋转方向为顺时针旋转时,
当塔机T1的吊臂旋转方向为逆时针旋转时,
设A,B为距离交叉区域的端点,B与X的距离小于或等于A与X的距离;运送货物时,塔机T1从B点离开交叉区域Q,使塔机T2可以进入交叉区域Q;所述双塔机作业任务为需要塔机T1从地面上的M点运送到N点;
t1表示塔机T1从启动到运送货物从M点至装卸点X点并离开交叉区域Q的时间长度;
表示塔机T1从S1位置开始,塔机T1吊臂与吊钩均到达M点的时间,当塔机T1在零时刻时已经装载货物,则取0;
S1表示零时刻时塔机T1的吊臂所在的位置;
S2表示零时刻时塔机T2的吊臂所在的位置;
ω1表示塔机T1的旋转角速度;
ω2表示塔机T2的旋转角速度;
νc1表示塔机T1的吊臂上的变幅小车的运行速度;
νc2表示塔机T2的吊臂上的变幅小车的运行速度;
lc1表示塔机T1的吊臂上的变幅小车的运行幅度;
lc2表示塔机T2的吊臂上的变幅小车的运行幅度;
νh1表示塔机T1的吊钩的起降速度;
νh2表示塔机T2的吊钩的起降速度;
lh1表示塔机T1的吊钩距离地面的高度;
lh2表示塔机T2的吊钩距离地面的高度;
lm为M点与塔机T1中心的距离;
ln为N点与塔机T2中心的距离;
lx1为装卸点X与塔机T1中心的距离;
lx2为装卸点X与塔机T2中心的距离;
为塔机T1的吊臂从S1到M’点的劣弧弧度,M’点为M点映射以塔机T1中心为圆心,塔机T1中心到S1的距离为半径的圆弧上的圆周位置;
为塔机T1的吊臂从M’至A的劣弧弧度,由A至X的距离;
为塔机T1的吊臂从M’至B的劣弧弧度,由B至X的距离;
为塔机T1的吊臂从X至B的距离。
优选的,所述当双塔机作业为高塔到低塔作业时,货物由塔机T1交于T2,且T1高于T2时,塔机T1和塔机T2具有一交叉区域Q,X为交叉区域S中的装卸点,双塔机作业所需的时间,具体计算方法为:
当塔机T2的吊臂顺时针旋转以接收货物,且塔机T2在零时刻启动时,
在t1时刻,塔机T2的吊臂可能在弧线上的一点运行,或者在B’停机等待塔机T1的吊臂退出交叉区域,tw表示在B’停机等待塔机T1的吊臂退出交叉区域的等待时间;
在塔机T1的作业圆周外定义一条虚线圆弧,所述虚线圆弧与所述塔机T1的作业圆周距离2米的安全距离,而A’、B’为塔机T2的吊臂与所述虚线圆弧的切点;
为塔机T2的吊臂从S2到B’点的劣弧弧度;
为塔机T2的吊臂从B’至X的劣弧弧度。
优选的,所述当双塔机作业为高塔到低塔作业时,货物由塔机T1交于T2,且T1高于T2时,塔机T1和塔机T2具有一交叉区域Q,X为交叉区域S中的装卸点,双塔机作业所需的时间,具体计算方法为:
货物从塔机T1到T2的一次传递T1→T2cw的时间Tx可以表示为塔机T2的等待时间tw与塔机T2的吊钩从S2到达X的时间;
其中,表示塔机T2的吊臂从S2到B’点,再从B’点至X的劣弧弧度;
货物从X到N的一次性传递时间TN为:
或,
其中,表示塔机T2的吊臂从X到B’点,再从B’点至N的劣弧弧度;表示塔机T2的吊臂从X到A’点,再从B’点至N的劣弧弧度。
优选的,所述当双塔机作业为高塔到低塔作业时,货物由塔机T1交于T2,且T1高于T2时,塔机T1和塔机T2具有一交叉区域Q,X为交叉区域S中的装卸点,双塔机作业所需的时间,具体计算方法为:
当塔机T2的吊臂逆时针旋转以接收货物,且塔机T2在零时刻启动时,
为塔机T2的吊臂从S2到B’点的劣弧弧度;
为塔机T2的吊臂从A’至X的劣弧弧度。
本申请有益效果如下:
本发明提供的基于遗传算法和MMAS算法的塔机群多任务的调度方法,结合遗传算法和MMAS算法寻找最优方案,提高多塔机多任务作业的效率。
附图说明
为了更清楚地说明本发明实施例或现有技术中的技术方案,下面将对实施例描述中所需要使用的附图作简单地介绍,显而易见地,下面描述中的附图仅仅是本发明的一些实施例。
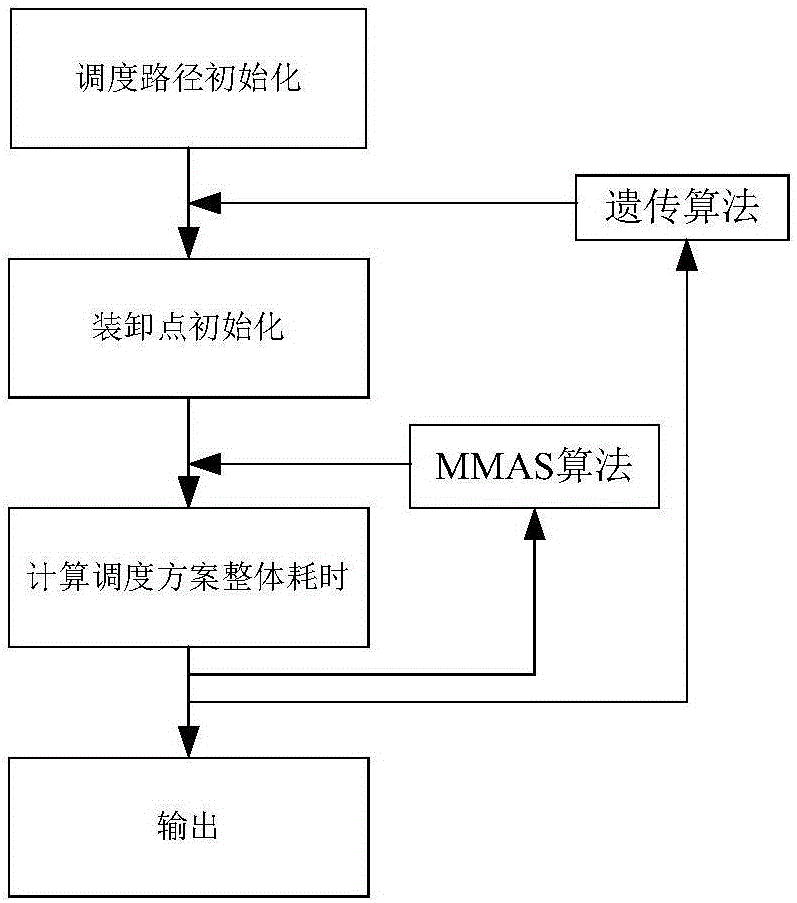
图1为本申请较佳实施方式基于遗传算法和MMAS算法的塔机群多任务的调度方法的流程图;
图2为本申请塔机群多任务调度一实施例的示意图;
图3为本申请双塔机作业一实施例的示意图;
图4为本申请双塔机作业高塔到低塔调度的一实施例的示意图;
图5为本申请双塔机作业低塔到高塔调度的一实施例的示意图;
图6为本申请采用MMAS算法第一阶段寻优的示意图;
图7为本申请采用MMAS算法第二阶段寻优的示意图;
图8为本申请蚂蚁在塔机群多任务问题中的解P{X}的示意图。
具体实施方式
为了更好的理解上述技术方案,下面将结合说明书附图以及具体的实施方式对上述技术方案进行详细的说明。
本申请提供的一种基于遗传算法和MMAS算法的塔机群多任务的调度方法,所述塔机群具有交叉区域,请参阅图1,所述调度方法包括:
步骤一,基于遗传算法,获取初始种群;随机在所述塔机群各任务选择D条调度路径作为遗传算法的初始种群,所述塔机群记为{T1,T2,……,Tn},Tn为第n个塔机;
步骤二,基于MMAS算法,获取初始路径;在所述塔机群各任务的交叉区域内,为所述选择的D条调度路径选择装卸点作为MMAS算法的初始路径;
步骤三,根据步骤一和步骤二中选择的遗传算法的初始种群和MMAS算法的初始路径,分解塔机群多任务路径为多次双塔机作业,计算所述多次双塔机作业所需的时间,最后一个塔机作业的完成时间为该调度方案总耗时;其中所述计算所述多次双塔机作业所需的时间具体为多次双塔机每条调度路径独立完成所需的时间;
其中,请参阅图2,图2为塔机群多任务路径的一实例,图2中七台塔机T1—T7作业范围相互相交,基于各塔机吊臂长度作为半径绘圆,圆内区域代表该塔机的作业覆盖范围。同时,有三个任务J1、J2、J3,需要将货物分别从M1、M2、M3运送至N1、N2、N3,各货物从起始点通过第一台塔机吊臂旋转运送至与其他塔机交叉区域内的某一点卸下,如图2中A、B、C所示,然后在一段时间后由第二台塔机前来装载并继续运送,直到完成作业。
所述步骤三中所述分解塔机群多任务路径为多次双塔机作业,计算所述多次双塔机作业所需的时间,最后一个塔机作业的完成时间为该调度方案总耗时,所述调度方案总耗时具体为:
Tj1=TX1+TX2+……+TXn-1+TN;
其中,Tj1为任务J1的调度方案总耗时,X1,X2,……,Xn-1为任务J1的调度方案的n-1个装卸点,TX1、TX2、……、TXn-1、TN分别为X1,X2,……,Xn-1的n段路径的耗时。
所述步骤三中所述分解塔机群多任务路径为多次双塔机作业,具体为:
所述塔机群多任务路径为Tnum111→Tnum12,num222→……→Tnum1n,num2nn;
将塔机群多任务路径分解为{(Tnum111→Tnum122),(Tnum222→Tnum133),……,(Tnum1n-1n-1→Tnum1nn),Tnum2nn};
其中,Tnum1n,num2nn为第n个塔机,且第n个塔机的吊臂具有两个旋转方向{num1n,num2n},cw表示顺时针旋转,aw表示逆时针旋转,其中num1n和num2n均可以取cw和aw两个值。
所述步骤三中所述计算所述多次双塔机作业所需的时间中,每次双塔机作业所需的时间,具体计算方法为:
通过计算确定双塔机吊臂合适的旋转方向以获得最小调度时长时所需的时间。
所述步骤三中所述计算所述多次双塔机作业所需的时间中,每次双塔机作业所需的时间,具体计算方法为:
当双塔机作业为高塔到低塔作业时,货物由塔机T1交于T2,且T1高于T2,塔机T1和塔机T2具有一交叉区域Q,X为交叉区域S中的装卸点,双塔机作业所需的时间取决于塔机吊臂旋转时间、变幅小车移动时间和吊钩起升/下放时间中的最大值。
所述当双塔机作业为高塔到低塔作业时,货物由塔机T1交于T2,且T1高于T2时,塔机T1和塔机T2具有一交叉区域Q,X为交叉区域S中的装卸点,双塔机作业所需的时间,请参阅图3,具体计算方法为:
当塔机T1的吊臂旋转方向为顺时针旋转时,
当塔机T1的吊臂旋转方向为逆时针旋转时,
设A,B为距离交叉区域的端点,B与X的距离小于或等于A与X的距离;运送货物时,塔机T1从B点离开交叉区域Q,使塔机T2可以进入交叉区域Q;所述双塔机作业任务为需要塔机T1从地面上的M点运送到N点;
t1表示塔机T1从启动到运送货物从M点至装卸点X点并离开交叉区域Q的时间长度;
表示塔机T1从S1位置开始,塔机T1吊臂与吊钩均到达M点的时间,当塔机T1在零时刻时已经装载货物,则取0;
S1表示零时刻时塔机T1的吊臂所在的位置;
S2表示零时刻时塔机T2的吊臂所在的位置;
ω1表示塔机T1的旋转角速度;
ω2表示塔机T2的旋转角速度;
νc1表示塔机T1的吊臂上的变幅小车的运行速度;
νc2表示塔机T2的吊臂上的变幅小车的运行速度;
lc1表示塔机T1的吊臂上的变幅小车的运行幅度;
lc2表示塔机T2的吊臂上的变幅小车的运行幅度;
νh1表示塔机T1的吊钩的起降速度;
νh2表示塔机T2的吊钩的起降速度;
lh1表示塔机T1的吊钩距离地面的高度;
lh2表示塔机T2的吊钩距离地面的高度;
lm为M点与塔机T1中心的距离;
ln为N点与塔机T2中心的距离;
lx1为装卸点X与塔机T1中心的距离;
lx2为装卸点X与塔机T2中心的距离;
为塔机T1的吊臂从S1到M’点的劣弧弧度,M’点为M点映射以塔机T1中心为圆心,塔机T1中心到S1的距离为半径的圆弧上的圆周位置;
为塔机T1的吊臂从M’至A的劣弧弧度,由A至X的距离;
为塔机T1的吊臂从M’至B的劣弧弧度,由B至X的距离;
为塔机T1的吊臂从X至B的距离。
所述当双塔机作业为高塔到低塔作业时,货物由塔机T1交于T2,且T1高于T2时,塔机T1和塔机T2具有一交叉区域Q,X为交叉区域S中的装卸点,双塔机作业所需的时间,具体计算方法为:
当塔机T2的吊臂顺时针旋转以接收货物,且塔机T2在零时刻启动时,
在t1时刻,塔机T2的吊臂可能在弧线上的一点运行,或者在B’停机等待塔机T1的吊臂退出交叉区域,tw表示在B’停机等待塔机T1的吊臂退出交叉区域的等待时间;
在塔机T1的作业圆周外定义一条虚线圆弧,所述虚线圆弧与所述塔机T1的作业圆周距离2米的安全距离,而A’、B’为塔机T2的吊臂与所述虚线圆弧的切点;
为塔机T2的吊臂从S2到B’点的劣弧弧度;
为塔机T2的吊臂从B’至X的劣弧弧度。
所述当双塔机作业为高塔到低塔作业时,货物由塔机T1交于T2,且T1高于T2时,塔机T1和塔机T2具有一交叉区域Q,X为交叉区域S中的装卸点,双塔机作业所需的时间,具体计算方法为:
货物从塔机T1到T2的一次传递T1→T2cw的时间Tx可以表示为塔机T2的等待时间tw与塔机T2的吊钩从S2到达X的时间;
其中,表示塔机T2的吊臂从S2到B’点,再从B’点至X的劣弧弧度;
货物从X到N的一次性传递时间TN为:
或,
其中,表示塔机T2的吊臂从X到B’点,再从B’点至N的劣弧弧度;表示塔机T2的吊臂从X到A’点,再从B’点至N的劣弧弧度。
请参阅图4,当塔机T2的吊臂逆时针旋转以接收货物,且塔机T2在零时刻启动时,
为塔机T2的吊臂从S2到B’点的劣弧弧度;
为塔机T2的吊臂从A’至X的劣弧弧度。
针对双塔机作业为低塔到高塔的情况
所述当双塔机作业为低塔到高塔作业时,货物由塔机T1交于T2,且T1低于T2时,塔机T1和塔机T2具有一交叉区域Q,X为交叉区域S中的装卸点,双塔机作业所需的时间,请参阅图3,具体计算方法为:
当塔机T1的吊臂旋转方向为顺时针旋转时,
当塔机T1的吊臂旋转方向为逆时针旋转时,
设A,B为距离交叉区域的端点,B与X的距离小于或等于A与X的距离;运送货物时,塔机T1从B点离开交叉区域Q,使塔机T2可以进入交叉区域Q;所述双塔机作业任务为需要塔机T1从地面上的M点运送到N点;
t1表示塔机T1从启动到运送货物从M点至装卸点X点并离开交叉区域Q的时间长度;
表示塔机T1从S1位置开始,塔机T1吊臂与吊钩均到达M点的时间,当塔机T1在零时刻时已经装载货物,则取0;
S1表示零时刻时塔机T1的吊臂所在的位置;
S2表示零时刻时塔机T2的吊臂所在的位置;
ω1表示塔机T1的旋转角速度;
ω2表示塔机T2的旋转角速度;
νc1表示塔机T1的吊臂上的变幅小车的运行速度;
νc2表示塔机T2的吊臂上的变幅小车的运行速度;
lc1表示塔机T1的吊臂上的变幅小车的运行幅度;
lc2表示塔机T2的吊臂上的变幅小车的运行幅度;
νh1表示塔机T1的吊钩的起降速度;
νh2表示塔机T2的吊钩的起降速度;
lh1表示塔机T1的吊钩距离地面的高度;
lh2表示塔机T2的吊钩距离地面的高度;
lm为M点与塔机T1中心的距离;
ln为N点与塔机T2中心的距离;
lx1为装卸点X与塔机T1中心的距离;
lx2为装卸点X与塔机T2中心的距离;
为塔机T1的吊臂从S1到M’点的劣弧弧度,M’点为M点映射以塔机T1中心为圆心,塔机T1中心到S1的距离为半径的圆弧上的圆周位置;
为塔机T1的吊臂从M’至A的劣弧弧度,由A至X的距离;
为塔机T1的吊臂从M’至B的劣弧弧度,由B至X的距离;
为塔机T1的吊臂从X至B的距离。
所述当双塔机作业为低塔到高塔作业时,货物由塔机T1交于T2,且T1低于T2时,塔机T1和塔机T2具有一交叉区域Q,X为交叉区域S中的装卸点,双塔机作业所需的时间,具体计算方法分两种情况为:
第一种情况,当塔机T2经逆时针到达X时,塔机T2需要在吊臂到达C点之前将小车收回到幅度小于ls,因而该段调动时间由段吊臂与小车运动时间的较大值以及段吊臂与小车运动时间的较大值组成,考虑到吊钩的下降时间,最终T2从启动到开始装载X点货物的时间可以表示为:的时间为:
C为塔机T1与T2的中心的连线与T2圆周的交点;
为塔机T2从S2到C的弧度;
为塔机T2从C到X的弧度;
ls为塔机T2的吊臂上的变幅小车的最小允许幅度,即塔机T2的吊臂上的变幅小车与虚线弧度的距离,所述虚线弧度为在塔机T1的作业圆周外定义的一条虚线圆弧,所述虚线圆弧与所述塔机T1的作业圆周距离2米的安全距离;
lc2表示塔机T2的吊臂上的变幅小车的运行幅度;
ω1表示塔机T1的旋转角速度;
νc1表示塔机T1的吊臂上的变幅小车的运行速度;
lx2为装卸点X与塔机T2中心的距离;
lh2表示塔机T2的吊钩距离地面的高度;
νh2表示塔机T2的吊钩的起降速度。
用tc表示塔机T2的吊臂上的变幅小车从进入虚线区域到抵达X点的时间为:
类似高塔到低塔情况中塔机T2延时启动的分析,将塔机T2的吊臂上的变幅小车在安全区域外等待T1退出的时间tw(如果存在的话)移动到T2启动之前,以保证T2塔机运动的连续性。延时时间tw可以表示为:
同样令tw=(tw+|tw|)/2,作业中从塔机T1→T2aw的传递时间为:
Tx=tw+tx。
第二种情况,当塔机T2经顺时针到达X时,旋臂不会经过两塔机中心连线,T2小车不用拉回到幅度ls。而是运动到与X等距的lx2,假设弧线上一点D使得T2吊臂在D点时小车的最大安全幅度与到X点的幅度相同为lx2,T2小车在该点进入安全区域。由T2延时启动保证连续运动的性质,此时T1正好退出安全区域,则有:
T1→T2cw的传递时间Tx为:
为塔机T2的吊臂从S2至B的劣弧弧度,由B至D的距离;
为塔机T2从D到X的弧度。
步骤四,将所述调度方案总耗时作为更新MMAS算法中的信息素,返回步骤二开始迭代寻找基于已定调度路径下使该调度方案总耗时最短的最优交接点,所述最优交接点为基于MMAS算法迭代至第一预设次数终止时调度方案总耗时最短的所述D条调度路径的装卸点;
步骤五,基于遗传算法,将步骤四中得到最短的调度方案总耗时作为参考保留优质种群,淘汰劣质种群,优质种群之间相互交叉生成新的种群以保证种群数量;返回步骤二开始迭代寻找最优种群,所述最优种群为基于遗传算法迭代至第二预设次数终止时最优种群为最优调度方案。
具体的,在所述步骤四之前,所述步骤三之后,所述调度方法还包括:
当所述塔机群为多作业并行情况时,基于防碰撞算法对塔机作业完成的时间以延迟等待的方式进行修正,获取最后一个塔机作业的完成时间为该调度方案总耗时。
针对遗传算法的调度路径选择,本申请采用实例来解释。
假设当前有m台塔机需要完成n个作业,以参与某一作业的塔机路径组合数进行计算,若编号为i的作业有Di条调度路径,则n个作业的调度组合方案共有D=D1×D2×……×Dn种。设置遗传算法的初始种群数量为
GN=δD
其中δ为小于1的正浮点数,根据D的大小设置合适的数值,一般取0.1-0.2。每个种群包含n条染色体,每条染色体的基因即为相应作业的一条调度路径。可以通过一个简单的规则来初步估计调度路径的好坏:每步交接均由当前点到达下个交叉区域最近的端点,由此得到该路径的参考时间TR。TR在一定程度上可以反应路径的好坏,但也并不总是这样,尤其某几台塔机特别繁忙的情况下。因此,为不同长度的调度路径赋予不同的权重,可以在保留长路径被选择概率的同时有效改善初始种群的质量。设置第j条参考时间为TRi的调度路径的权重
则该路径被染色体选择的概率可以通过以下式子得到:
一条完整的染色体除了包含该作业的调度路径,还需具有该路径上各交叉区域内的交接点集合P{X},这样代表n个任务的n条染色体即可构成一套完整的调度方案。通过求取该调度方案的完成时间,即可得到该种群的适应度。如果以P*{X}表示该种群内能够使全部作业完成时间最短的n个P{X}的集合,则得到P*{X}即为最优调度方案。但由于多任务间相互约束,很难在多项式时间内得到真正的最短时间。故考虑使用蚁群算法渐进地逼近P*{X}。本申请采用的MMAS算法(最大最小蚁群算法)来渐进逼近。
下面将针对MMAS算法选择交叉区域中装卸点位置做详细解释。
根据问题规模,为每个种群添加m只蚂蚁,从J1到Jn遍历调度方案的每个交接区域,并在其中选择一个点作为可能的最优点访问。以米为单位将交叉区域网格化,使区域上的无穷个点得以离散为包含有限个点的集合。一般而言,当X在交叉区域两端点的连线方向上变化时主要影响两塔机吊臂旋转时间,因而对作业时间影响较大;而在两塔机中心连线方向上变化时主要影响小车变幅时间而对作业时间影响相对较小。
因此,为了提升蚂蚁的寻优速度,将蚂蚁的寻优过程分为两个阶段。首先在初始阶段将蚂蚁可以访问的点限定在交叉区域连线左右一米范围内。如图6所示,在初始时刻,蚂蚁不会在所有网格上的点进行尝试,而是在虚线框内的点集p1-pk中寻求它们当中的最优解。假设迭代求得pj为该点集中的最优解,则继续在两塔机中心连线方向上的pj邻域点集中寻求最优解,如图6和图7所示。
如果要求精度较高,在种群内迭代结束后,可以对输出P{X}的邻域再度离散化(以0.5米的精度或者更小),以获得更加逼近P*{X}的解。由此将求解P*{X}在连续域内的寻优问题转变为多级决策问题,蚂蚁在该问题中的解可用图8来表示:
在角速度为ω的塔机上,同一作业中的两相邻交接点Xi转移到Xj的概率通过下式计算:
其中初始时刻各路径上信息素τ(0)=C,C为一任意常数值。u表示当前可选点集的容量。Xi到Xj的能见度ηij=ω/XiXj。如果Xi属于该作业的第一个交接点,则ηij=ω/MXi。
基于MMAS(Max-Min Ant System,最大-最小蚁群算法),将各条路径上的信息素限制在[τmin,τmax],τmin可以有效避免算法停滞,τmax可以避免因某条路径上的信息素远大于其他路径而导致算法早熟。所有蚂蚁中只有精英蚂蚁(总调度时间最短的蚂蚁)可以留下信息素,路径上的信息素强度按照下式进行更新:
τij(t+n)=ρ·τij(t)+Δτij
式中ρ(0≤ρ<1)为信息素的残留系数,代表轨迹的持久性,Δτij表示精英蚂蚁在路径(Xi,Xj)上所留下的信息素,可以通过下式计算:
其中,Q是常数,其大小决定了算法的收敛速度,但如果取值过大容易使算法很快陷入停滞。Ttotal表示基于精英蚂蚁此次路径(即全部作业完成)的总调度时间。
基于连续域函数小范围单调特性,对精英蚂蚁的路径集合P{X}中的每个X点的邻域进行搜索,如果新解集优于当前解,则采纳新的解集;如果新解集与P{X}所获得总调度时间相同,则为该区域范围性添加信息素。
经过Naco次迭代获得该种群的调度时间后,与其他种群进行对比,并淘汰时间较长的种群。淘汰率取决于种群内部蚁群算法的迭代次数,如果迭代次数较少,淘汰率也可以相对偏小,以保证尽可能不会错误地淘汰优秀种群。
筛选后最优秀的两个种群之间相互杂交,即随机地交换两者在同一作业中不同的调度路径,并产生新的种群。如果前两名种群的染色体完全一致,可以通过随机变异某一作业调度路径的方式产生子代种群。由于短时间内无法判断子代的优劣,因此将子代种群与筛选留下的父代一同参与迭代,经过Nga次循环后得到最优解。整个算法的循环次数可以由式子NC=Nga×Naco表示,Naco与Nga的大小取决于问题规模。
本申请有益效果如下:
本发明提供的基于遗传算法和MMAS算法的塔机群多任务的调度方法,结合遗传算法和MMAS算法寻找最优方案,提高多塔机多任务作业的效率。
最后所应说明的是,以上具体实施方式仅用以说明本发明的技术方案而非限制,尽管参照实例对本发明进行了详细说明,本领域的普通技术人员应当理解,可以对本发明的技术方案进行修改或者等同替换,而不脱离本发明技术方案的精神和范围,其均应涵盖在本发明的权利要求范围当中。
- 还没有人留言评论。精彩留言会获得点赞!