一种基于频率自适应的分数补偿重复控制器的磁悬浮转子谐波电流抑制方法与流程

本发明涉及磁悬浮转子谐波电流抑制的技术领域，具体涉及一种基于整数延时与分数阶重复控制器相结合的磁悬浮转子谐波电流抑制方法，用于磁悬浮陀螺或者磁悬浮飞轮的谐波电流抑制，为磁悬浮飞轮或陀螺在“超静”卫星平台上的应用提供技术支持。

背景技术：

磁悬浮转子采用磁轴承支撑的方式，由于磁轴承转子系统具有长寿命、无摩擦和主动振动可控等优点，适用于各种高速旋转设备，在航天、航空、核事业和机械工程领域等领域具有广泛的应用前景，特别是在磁悬浮飞轮、磁悬浮陀螺和磁悬浮分子泵等方面有良好的应用。

在实际情况中，由于机械加工精度有限和材料不均匀等因素的影响，磁悬浮转子无法避免的会出现质量不平衡，在高速转动过程中会产生与转速频率相同的同频扰动；另一方面，由于传感器检测面、检测表面电或磁特性不一致，会产生同频及倍频的扰动信号，也即是传感器谐波，传感器谐波会引发谐波控制电流。谐波控制电流进而引发磁轴承产生谐波振动力，振动通过磁轴承传递到基座进而传递给航天器，影响航天器指向精度和稳定精度。

在谐波电流抑制算法中，根据算法能否同时抑制多种频率成分，可以将其归为以下两类：一类是单一频率抑制，若要对多频率成分的谐波信号进行抑制需要该类算法的叠加，如并联多个陷波器或多个LMS滤波器等。该方法复杂度和计算量大，且需考虑不同频率扰动抑制算法的收敛速度，谐波抑制性能低，不利于工程化应用。另一类算法是不需要多个算法的累加，单一算法即可实现对多种频率成分扰动的同时抑制，也即是重复控制算法。重复控制算法基于内模原理，能够对周期已知、幅值不确定，包含多种频率成分的周期性扰动信号进行有效地抑制，本质是通过将外部信号的等效数学模型植入到控制器内部，从而实现对外部输入信号跟踪或抑制作用。重复控制算法具有计算量小、结构简单、占用内存小和易于实现等优点，适用于主动磁轴承系统多种倍频的抑制。如图4所示的重复控制算法，只能针对特定的转子转速进行电流抑制，一旦采样频率与谐波干扰信号基频的比值不为整数时，无法对小数部分进行补偿，也即是无法做到在任意额定频率下对谐波扰动信号的精确抑制。

技术实现要素：

本发明的目的：克服现有传统控制器的不足，发明一种不受低通滤波器限制，并且在采样频率与谐波电流基频的比值为分数情况下，能进行补偿的频率自适应分数阶重复控制算法。

本发明的技术解决方案：一种基于频率自适应的分数补偿重复控制器的磁悬浮转子谐波电流抑制方法，其特征在于包括以下步骤：

步骤(1)建立包含不平衡质量和传感器谐波的磁悬浮转子动力学模型

根据牛顿第二定律，磁悬浮转子在X方向的动力学方程为：

其中，表示转子在X方向的加速度，m表示转子质量，f_x表示磁轴承在X方向的轴承力，f_u表示转子的不平衡力，可表示为：

f_u＝meΩ²cos(Ωt+φ)

其中e表示转子几何中心与质心之间的偏差，Ω表示转子转速，φ表示转子不平衡质量的初始相位；

当转子围绕磁轴承中心悬浮时，磁轴承的电磁力可表示为线性化方程：

f_x≈K_xx+K_ii

其中K_x和K_i分别表示磁轴承位移刚度和电流刚度，i表示磁轴承线圈控制电流；

由于机械加工精度和材料的不均匀因素的影响，磁悬浮转子的位移传感器检测面会出现圆度不理想、材质不均匀、剩磁特性不同因素，位移传感器的输出将会出现同频和倍频的多谐波信号，则位移传感器的输出可表示为：

x_s(t)＝x(t)+x_d(t)

其中x(t)表示转子几何中心真实的坐标值，x_s(t)表示传感器的输出值，x_d(t)为传感器输出值与真实值的误差，可表示为：

其中l表示谐波次数，c_l表示谐波系数，θ_l表示谐波初始相位；

将i、x_d(t)、f_u依次进行拉普拉斯变换可得i(s)、x_d(s)、f_u(s)，则磁轴承电流i(s)的传递函数可表示为：

其中G_c(s)是控制器的传递函数，G_w(s)是功放环节的传递函数，G_p(s)是磁悬浮转子的传递函数，其中R(s)表示参考输入信号，K_s表示传感器增益；

步骤(2)：基于频率自适应的分数补偿重复控制器的建立

定义N为系统采样频率与谐波信号基频的比值，同时N的大小可体现出分数重复控制器的控制分辨率的高低，一般采样频率越高意味着控制精度越高。在工程实际应用中，分数延时环节无法直接实现，需要找到一种替换形式。分数阶延时环节可用一种拉格朗日插值多项式来替代；

步骤(3)：基于频率自适应的分数补偿重复控制器的稳定性分析

为了便于系统的稳定性分析，引入重复控制器的重构谱R(ω)。重构谱函数作为判断系统稳定性的一种依据：根据最小增益理论可知，对于一个稳定系统，如果加入重复控制器后系统重构谱函数能满足R(ω)<1，则新系统也是稳定的。

步骤(4)：设计基于频率自适应的分数补偿重复控制器的谐波电流抑制算法的子步骤

当系统采样频率与谐波信号基频的比值不为整数时，为了实现对小数部分的补偿，如图5所示，以从G_w(s)输出的电流i作为重复控制器的输入，经过整数延时和分数延时相串联的频率自适应分数补偿重复控制器，重复控制器的输出和控制器G_c(s)的输出一起作为G_w(s)的输入，同时将低通滤波器Q(s)由反馈回路内移动到与重复控制器相串联的支路上。采用以上所述系统结构，一方面消除低通滤波器幅值衰减和相位滞后带来的影响，使得系统在高频段也能实现电流抑制，另一方面在采样频率与谐波扰动信号基频比值不为整数时，可以实现分数阶补偿，从而提高任意额定转速下磁轴承的谐波电流抑制精度。

以外部参考输入信号R(s)和谐波扰动等效信号D(s)作为输入，以磁轴承线圈电流i(s)作为输出，加入分数阶重复控制器时的灵敏度函数S₂(s)可表示如下：

其中，表示未加重复控制器时系统的灵敏度函数,N₁表示采样的整周期数，N₂表示超前相位补偿周期数，A表示小数补偿周期数，并且N＝N₁+N₂+A，说明当N为分数时，也能使得灵敏度函数S₂(s)幅值为零，并且不受低通滤波器的影响。K_f(s)为相位补偿函数和K_rc为增益调节参数，低通滤波器Q(s)的截止频率ω_c大于有效谐波扰动的最高频率ω_max，在ω∈(0,ω_max)范围内Q(s)的幅值衰减和相位滞后很小，|Q(s)|≈1，arg[Q(s)]_s＝jω≈0。

更进一步的，所述步骤(2)分数阶延时环节可表示为：

是采样周期的整数延时环节，重复控制器的相位超前补偿环节。由于并且N₁+N₂＝int[N]作为N的整数部分，所以有A＝N-(N₁+N₂)，0＜A＜1作为N的分数部分。分数阶延时环节可用一种拉格朗日插值多项式来表示：

其中系数D_l可表示如下：

本发明基本原理：由于质量不平衡和传感器谐波的存在，主动磁轴承会产生谐波电流，从而引起谐波振动，影响磁悬浮转子的工作状态。本发明针对谐波电流进行抑制，减小谐波振动。通过建立含质量不平衡和传感器谐波的磁悬浮转子动力学模型，分析系统的谐波电流，提出了一种频率自适应的分数补偿重复控制器，从而实现磁悬浮转子高转速下谐波电流抑制，重点从两个方面进行研究：分数阶延时环节的设计，引入分数延时滤波器替代分数延时环节，当转子的转速发生改变的时候，可通过在线改变分数延时滤波器的系数实现小数部分精确补偿；通过设计相位补偿环节以保证稳定性，最终实现任意转速下磁悬浮转子谐波电流的精确抑制。

本发明与现有技术相比的优点在于：把低通滤波器从反馈回路内移动到与重复控制器相串联的支路上，有效的消除了由于低通滤波器幅值衰减和相位滞后带来的影响，引入分数补偿环节，使得系统有对分数具有补偿的能力，使得系统能在任意额定的采样频率下，能实现对谐波扰动信号的精确抑制。

附图说明

图1为本发明的流程图；

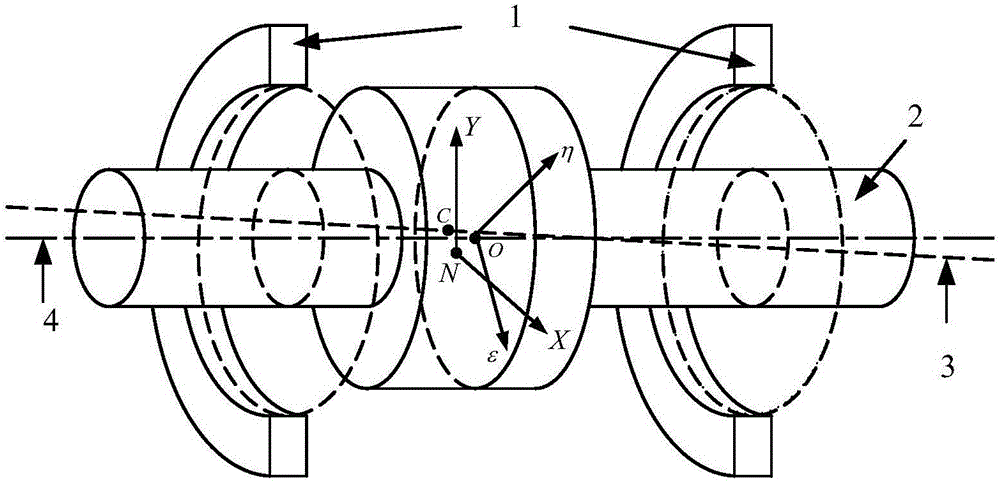
图2为磁悬浮转子系统结构示意图，其中，1为磁轴承，2为转子，3为惯性主轴，4为几何轴；

图3为X通道磁轴承转子控制系统方框图；

图4为传统重复控制器系统方框图；

图5为分数阶重复控制器系统方框图；

图6为简化后的改进重复控制器系统方框图；

图7为磁轴承转子在75Hz下的谐波电流抑制结果。其中图7a为不加振动抑制算法，图7b为加入本发明所述方法的重复控制器。

具体实施方式

下面结合附图以及具体实例进一步说明本发明。

如图1所示，一种基于频率自适应的分数补偿重复控制器的磁悬浮转子谐波电流抑制方法的实施过程是：首先建立含质量不平衡和传感器谐波的磁悬浮转子动力学模型，然后设计一种基于频率自适应的分数补偿重复控制器的磁悬浮转子谐波电流抑制方法。

磁悬浮转子系统由位移传感器K_s、控制器G_c(s)、功率放大器G_w(s)和磁悬浮转子G_p(s)组成，位移传感器测量出转子位移并反馈至控制器，控制器输出控制量至功率放大器，功率放大器输出电流到磁轴承线圈，磁轴承产生力和力矩使转子稳定悬浮。由于机械加工精度有限，磁悬浮转子无法避免的会出现质量不平衡；由于传感器检测面、检测表面电或磁特性不一致，会产生同频及倍频的扰动信号，也即是传感器谐波。

步骤(1)建立包含不平衡质量和传感器谐波的磁悬浮转子的数学模型

磁悬浮转子除了由电机控制的轴向旋转自由度外，其他五个自由度均是由主动磁轴承来控制。其系统结构示意图如图2所示，两个径向通道的平动被主动磁轴承控制。C表示转子的质心，N表示磁轴承定子的几何中心，以N为中心建立惯性坐标系NXY。O表示转子的几何中心，以O为中心建立旋转坐标系Oεη。由于转子结构是对称的，所以转子在X和Y方向有相同的数学模型，根据牛顿第二定律，磁悬浮转子在X方向的动力学方程为：

其中，表示转子在X方向的加速度，m表示转子质量，f_x表示磁轴承在X方向的轴承力，f_u表示转子的不平衡力，可表示为：

f_u＝meΩ²cos(Ωt+φ)

其中e表示转子几何中心与质心之间的偏差，Ω表示转子转速，φ表示转子不平衡质量的初始相位；

当转子围绕磁轴承中心悬浮时，磁轴承转子的电磁力可表示为线性化方程：

f_x≈K_xx+K_ii

其中K_x和K_i分别表示磁轴承位移刚度和电流刚度，i表示磁轴承线圈控制电流；

由于机械加工精度和材料的不均匀等因素的影响，磁悬浮转子的位移传感器检测面会出现圆度不理想、材质不均匀、剩磁特性不同等因素，位移传感器的输出将会出现同频和倍频的多谐波信号，则位移传感器的输出可表示为：

x_s(t)＝x(t)+x_d(t)

其中x(t)表示转子几何中心真实的坐标值，x_s(t)表示传感器的输出值，x_d(t)为传感器输出值与真实值的误差，可表示为：

其中l表示谐波次数，c_l表示谐波系数，θ_l表示谐波初始相位。式中，当l＝1时，表示位移传感器输出中存在同频信号，而当l＝2、3、4.......时，表示位移传感器中包含倍频信号，也即是系统中存在多次谐波。

磁悬浮转子在Y方向的动力学方程为：

其中，表示转子在Y方向的加速度，m表示转子质量，f_y表示磁轴承在Y方向的轴承力，f_u表示转子的不平衡力，可表示为：

f_u＝meΩ²cos(Ωt+φ)

其中e表示转子几何中心与质心之间的偏差，Ω表示转子转速，φ表示转子不平衡质量的初始相位；

当转子围绕磁轴承中心悬浮时，磁轴承转子的电磁力可表示为线性化方程：

f_y≈K_yy+K_ii

其中K_y和K_i分别表示磁轴承位移刚度和电流刚度，i表示磁轴承线圈控制电流；

则位移传感器的输出可表示为：

y_s(t)＝y(t)+y_d(t)

其中y(t)表示转子几何中心真实的坐标值，y_s(t)表示传感器的输出值，y_d(t)为传感器输出值与真实值的误差，可表示为：

其中l表示谐波次数，c_l表示谐波系数，θ_l表示谐波初始相位。式中，当l＝1时，表示位移传感器输出中存在同频信号，而当l＝2、3、4.......时，表示位移传感器中包含倍频信号，也即是系统中存在多次谐波。

将i、x_d(t)、f_u依次进行拉普拉斯变换可得i(s)、x_d(s)、f_u(s)。从图3可看出，此时未加重复控制算法，以外部参考信号R(s)为输入，通过只由G_c(s)、G_w(s)、G_p(s)和K_s反馈回路组成的系统，最终输出信号还叠加了f_u和x_d(t)/y_d(t)引起的输出，由此可得磁轴承电流i(s)的传递函数可表示为：

或

其中G_c(s)是控制器的传递函数，G_w(s)是功放环节的传递函数，G_p(s)是磁悬浮转子的传递函数，其中R(s)表示参考输入信号，K_s表示传感器增益；

结合以上分析可得，转子质量不平衡以及传感器误差会使得磁轴承产生谐波控制电流，从而产生谐波振动。

步骤(2)：基于频率自适应的分数补偿重复控制器的建立

定义N为系统采样频率与谐波信号基频的比值，同时N的大小可体现出分数阶重复控制器的控制分辨率的高低，一般采样频率越高意味着控制精度越高。由于并且N₁+N₂＝int[N]作为N的整数部分，所以有A＝N-(N₁+N₂)，0＜A＜1作为N的分数部分。在工程实际应用中，分数延时环节无法直接实现，需要找到一种替换形式。分数阶延时环节可用一种拉格朗日插值多项式来表示：

其中系数D_l可表示如下：

根据拉格朗日插值方法，多项式与分数延时环节的差值R_n可表示如下：

其中ξ∈[T_k,T_k+1]，T_k和T_k+1分别代表第k个和第k+1个的采样时刻，随着拉格朗日插值多项式阶数n的增大，近似余项R_n逐渐减小，即拉格朗日插值多项式的近似程度逐渐升高，但是，随着n的增大，算法计算量将大幅度增大。在实际工程中，应该综合考虑差值R_n和算法计算量两个因素，本发明中选用n＝1，则有

步骤(3)基于频率自适应的分数补偿重复控制器的分数补偿的稳定性分析

引入了分数阶补偿环节后，在ω∈(0,ω_c)频率范围内，分数阶延时环节可用一种拉格朗日插值多项式来表示，也即多项式的相位为-A·T_sω，幅值为在加入算法后对系统进行稳定性分析，可得如下：

当ω∈(0,ω_c)时，如图5所示，引入分数补偿环节，采用整数延时和分数延时相串联的频率自适应分数补偿重复控制器，并加入相应的相位补偿函数，同时将低通滤波器Q(s)由反馈回路内移动到与重复控制器相串联的支路上。图5经过简化得到图6，图6中分数延时环节已经被分数延时滤波器替代，且与高频段的相位补偿相串联，其中相位补偿函数C(s)可以表示为：

其中K_rc表示改进重复控制器增益，K_f(s)表示在低频段和中频段的相位补偿函数，表示高频段的相位补偿函数。

由图6可以得到加入改进重复控制器后系统的闭环特征方程，表示如下：

其中，M(s)＝1+G_c(s)G_w(s)G_p(s)K_s，

为了便于系统的稳定性分析，引入改进重复控制器后的重构谱，重构谱的定义如下：

重构谱函数可以作为判断系统稳定性的一种依据：根据最小增益理论可知，对于一个稳定系统，如果加入重复控制器后系统重构谱函数能满足R(ω)＜1，ω∈(0,ω_c)，则新系统也是稳定的。

定义系统函数F(s)：

其中，|F(s)|_s＝jω＝L(ω)e^jθ(ω)，加入重复控制器后系统的重构谱函数为：

其中取λ(ω)＝θ(ω)+θ_b(ω)+(N₂+A)T_sω，上式通过欧拉公式可得：

|1+K_rcL(ω)·K_b(ω)cosλ(ω)+jK_rcL(ω)·K_b(ω)sinλ(ω)|＜1

对上式两边分别进行取模的平方，可以得到：

[K_rcL(ω)·K_b(ω)]²＜-2K_rcL(ω)·K_b(ω)cosλ(ω)

因为重复控制器的增益K_rc＞0，且L(ω)＞0，K_b(ω)＞0，所以上式可简化为：

K_rcL(ω)·K_b(ω)＜-2cosλ(ω)

要使得上式恒成立，必须保证cosλ(ω)＜0，也即是：

90°＜λ(ω)＜270°

综上所述，通过串联合适的相位补偿函数和增益系数，可以保证加入算法后系统的稳定性。

步骤(4)设计基于频率自适应的分数补偿重复控制器的谐波电流抑制算法的子步骤

重复控制器基于内模原理，能消除输入信号中的谐波分量，在实际的磁轴承控制系统中，采样频率与谐波干扰信号基频的比值不一定为整数，从而需要对小数部分进行补偿，现有的针对磁轴承谐波电流抑制的重复控制器只能对其整数部分进行补偿，这样使得谐波电流抑制的精度大大降低，针对这一不足，本发明采用整数延时和分数延时相串联频率自适应分数补偿重复控制器。如图5所示，是采样周期的整数延时环节，重复控制器的相位超前补偿环节，是采样周期的分数阶延时环节，由分数延时滤波器替代得到。以从G_w(s)输出的电流i作为重复控制器的输入，经过整数延时和分数延时相串联的频率自适应分数补偿重复控制器，重复控制器的输出和控制器G_c(s)的输出一起作为G_w(s)的输入，同时将低通滤波器Q(s)由反馈回路内移动到与重复控制器相串联的支路上。分数补偿环节由分数延时滤波器替代，当谐波电流基频发生改变时，会得到一个新的小数，把小数带入分数延时滤波器确定分数延时滤波器的系数，从而实现分数延时滤波器的系数更新，进而可实现对小数部分进行补偿。采用以上的串联形式，一方面消除低通滤波器幅值衰减和相位滞后带来的影响，使得系统在高频段也能实现电流抑制，另一方面在采样频率与谐波扰动信号基频比值不为整数时，可以实现分数阶补偿，从而提高任意额定转速下磁轴承的谐波电流抑制精度，实现任意额定转速下的磁轴承谐波电流精确抑制。

以外部参考输入信号R(s)和谐波扰动等效信号D(s)作为输入，此时磁轴承线圈电流i(s)作为输出的灵敏度函数S₂(s)可表示如下：

其中，表示未加重复控制器前的系统的灵敏度函数,N₁表示采样的整周期数，N₂表示超前相位补偿周期数，A表示小数补偿周期数，并且N＝N₁+N₂+A，说明当N为分数时，也能使得灵敏度函数S₂(s)幅值为零，并且不受低通滤波器的影响。K_f(s)为相位补偿函数和K_rc为增益调节参数，低通滤波器Q(s)的截止频率ω_c大于有效谐波扰动的最高频率ω_max，在ω∈(0,ω_max)范围内Q(s)的幅值衰减和相位滞后很小，|Q(s)|≈1，arg[Q(s)]_s＝_jω≈0。

磁轴承转子在转速为4500rpm(75Hz)下的谐波电流频域和时域结果如图7所示，采用本发明的频率自适应分数补偿重复控制器与传统的重复控制器相比，电流的抑制效果明显的提高。图7(a)为不加重复控制器时电流图，图7(b)为加入本发明的分数阶重复控制器电流抑制效果图。通过对比图7(a)和图7(b)可得知道加入分数阶重复控制器前后磁轴承电流时域变化情况：从87mA降到12.4mA，降低了85.7％；频域变化情况：同频(从-22dB降低至-73dB，减少了99.7％)，二倍频(从-45dB降低至-75dB，减少了96.8％)，三倍频(从-48dB降低至-71dB，减少了92.9％)，四倍频(从-58dB降低至-77dB，减少了88.8％)，五倍频(从-57dB降低至-76dB，减少了88.8％)，从以上分析可知，加入分数阶重复控制器可以有效的抑制各个频段的谐波电流，所以本发明方法简明有效。

本发明未详细阐述部分属于本领域专业人员公知的现有技术。