考虑全捷联导引头视场约束的制导控制一体化设计方法与流程

本发明涉及一种制导控制一体化设计方法，特别涉及一种考虑全捷联导引头视场约束的制导控制一体化设计方法。

背景技术：

随着技术的发展，无人机载武器和单兵制导武器逐渐向小型化和低成本化方向发展，其典型特点是采用全捷联体制导引头以减小体积，降低成本，这种方式非常适合空间有限的导弹。然而，此类导弹的导引头光轴与弹体姿态固联，这使得传统基于惯性弹目视线角速度的制导方法无法直接使用，并且在姿态扰动影响下容易引起视场角超限，从而导致脱靶。

针对全捷联导弹制导控制系统设计主要是首先基于惯组信息和体视线角信息进行视线解耦，获取惯性系视线角速度信息，然后再采用频谱分离思想分别对制导系统和控制系统进行独立设计。这种设计方法存在较大的保守性，针对射程较近的单兵武器而言容易失稳。为了提高制导控制系统的综合性能，确保飞行过程的稳定性，基于Lyapunov稳定性理论开展制导控制系统的一体化设计成为有效的解决途径。目前该领域研究的主要进展有：考虑导引头视场限制的先进制导方法和考虑终端角度约束的制导控制一体化设计方法。

文献1“带导引头视场限制的多约束导引律及剩余时间估计，系统工程与电子技术，2014,Vol.36(8),p1609-1613”公开了一种考虑导引头视场限制的制导方法。该方法采用余弦函数的非线性特性，在传统攻击角度约束比例导引律的基础上增加了附加约束项，满足了攻击过程导引头视场约束。该方法在数学建模过程中假设导弹飞行过程中攻角很小可以忽略，由此避免了弹体姿态对视场角约束的影响，然而，全捷联导引头视场角超限问题通常主要是由于姿态扰动引起的，因此该方法具有局限性。

文献2“带终端角度约束的飞行器三维制导控制一体化设计，航天控制，2016,Vol.34(2),p3-8”公开了一种满足终端攻击角度约束的STT飞行器制导控制一体化设计方法。该方法结合鲁棒动态逆和动态面分块设计方法，满足了三维攻击过程的终端角度约束。然而，终端角是属于制导范畴的物理量，满足终端角度约束并不能从根本上确保视场角度满足约束，因此该方法无法确保全捷联导引体制下的视场角限制。

综上所述，现有制导控制方法难以从理论上同时满足制导精度和全捷联导引头视场角约束条件，并且国内外针对全捷联视场约束下的制导控制一体化设计方法还未见公开文献。

技术实现要素：

为了克服现有制导控制一体化设计方法实用性差的不足，本发明提供一种考虑全捷联导引头视场约束的制导控制一体化设计方法。该方法首先建立导弹纵向通道姿态控制系统模型、纵向平面内导弹-目标的相对运动模型以及全捷联导引头纵向通道视线解耦模型；再选择状态变量和系统输出变量，建立考虑视场角约束的制导控制一体化状态空间数学模型；采用障碍Lyapunov函数、扩张状态观测器以及动态面控制相结合的控制方法。由于采用障碍Lyapunov函数、扩张状态观测器以及动态面控制相结合的控制方法，同时满足了制导精度和全捷联导引头视场角约束条件，保证了导弹制导控制过程中全捷联导引头探测的体视线角满足导引头试场约束。

本发明解决其技术问题所采用的技术方案：一种考虑全捷联导引头视场约束的制导控制一体化设计方法，其特点是包括以下步骤：

步骤一、建立导弹纵向通道姿态控制系统模型、纵向平面内导弹-目标的相对运动模型以及全捷联导引头纵向通道视线解耦模型；

(a)建立导弹纵向通道姿态控制系统模型。

其中，α是导弹的飞行攻角，ω_z是导弹的俯仰角速度，δ是导弹的俯仰舵偏角；P是导弹的发动机推力，m是导弹的质量，J_z是导弹的转动惯量，V_M是导弹的飞行速度；q是导弹的飞行动压，S是导弹的参考面积，L是导弹的参考长度；是升力系数对攻角的偏导数，是升力系数对舵偏角的偏导数，是俯仰力矩系数对攻角的偏导数，是俯仰力矩系数对舵偏角的偏导数，是俯仰阻尼力矩系数；Δ_α是攻角微分方程的不确定性，Δ_ω是角速度微分方程的不确定性。

(b)建立纵向平面内导弹-目标的相对运动模型。

其中，q是弹-目相对视线角，是弹-目相对视线角速度，是弹-目相对视线角加速度，r是弹-目相对距离，是弹-目相对速度；A_M是导弹的加速度，A_T是目标的加速度；θ_M是导弹运动的弹道角，θ_T是目标运动的弹道角；V_M是导弹的飞行速度，V_T是目标的飞行速度。

(c)建立全捷联导引头纵向通道视线解耦模型。

其中，q_ε为捷联导引头测量到的目标体视线角。

步骤二、选择状态变量和系统输出变量，建立考虑视场角约束的制导控制一体化状态空间数学模型；

对于地面固定目标进行精确打击时，认为A_T＝0,V_T＝0,θ_T＝0。因此选择状态变量为：得到系统的状态空间模型如下：

其中，Δ₁为第一个状态方程的综合不确定性，Δ₂为第二个状态方程的综合不确定性，Δ₃为第三个状态方程的综合不确定性，Δ₄为第四个状态方程的综合不确定性；u是待设计的系统控制输入。

步骤三、给定视场角约束边界，基于障碍Lyapunov函数和反步法设计对应于视线角速度第一层虚拟控制量；

定义误差项e₁＝x₁和e₂＝x₂-x_2d，其中x_2d是待设计的状态x₂的虚拟控制。为了确保失调角满足要求|x₁|≤Q，Q为需要约束的视场角范围，选择障碍Lyapunov函数如下：

当设计虚拟控制K₁>0时，其微分为：

步骤四、根据视线角速度跟踪误差，基于Lyapunov稳定性理论设计对应于飞行攻角的第二层虚拟控制量；

定义攻角状态的误差项e₃＝x₃-x_3d，选择新的Lyapunov函数为：

当设计虚拟控制K₂>0时，其微分为：

步骤五、根据飞行攻角跟踪误差，基于Lyapunov稳定性理论设计对应于姿态角速度的第三层虚拟控制量；

定义俯仰角速度状态的误差项e₄＝x₄-x_4d，选择新的Lyapunov函数为：

当设计虚拟控制K₃>0时，其微分为：

步骤六、根据姿态角速度跟踪误差，基于Lyapunov稳定性理论综合设计俯仰通道制导控制一体化的理想舵偏角指令；

选择新的Lyapunov函数为：

对其求导得到：

当设计虚拟控制K₄>0时，其微分为：

步骤七、针对步骤三～步骤五所对应的虚拟控制量微分问题，引入动态面一阶延迟予以替代；

其中，x_ic，i＝2,3,4是步骤3～步骤5中虚拟控制量x_id，i＝2,3,4的近似量，τ_i，i＝2,3,4是相应动态面的时间延迟参数。

步骤八、针对步骤七中对虚拟控制量近似微分带来的信号偏差以及制导控制一体化状态空间数学模型各通道干扰带来的模型不确定问题，采用干扰观测器进行干扰的在线估计；给出干扰观测器表达式如下：

其中，z₁₀是系统状态x₁的估计值，z₂₀是系统状态x₂的估计值，z₃₀是系统状态x₃的估计值，z₄₀是系统状态x₄的估计值；z₁₁是系统方程组(4)中第一个方程不确定性Δ₁的估计值，z₂₁是系统方程组(4)中第二个方程不确定性Δ₂的估计值，z₃₁是系统方程组(4)中第三个方程不确定性Δ₃的估计值，z₄₁是系统方程组(4)中第四个方程不确定性Δ₄的估计值；非线性函数fal(e_i′,α_i,σ_i)表达式如下：

步骤九、结合步骤六～步骤八设计结果综合得到最终考虑全捷联导引头视场角约束的制导控制一体化设计结果。给出最终的控制器表达式如下：

其中，η₁>0是对应第一个状态的可调参数，η₂>0是对应第二个状态的可调参数，η₃>0是对应第三个状态的可调参数，η₄>0是对应第四个状态的可调参数；sign(e_i),i＝1…4是标准符号函数。

本发明的有益效果是：该方法首先建立导弹纵向通道姿态控制系统模型、纵向平面内导弹-目标的相对运动模型以及全捷联导引头纵向通道视线解耦模型；再选择状态变量和系统输出变量，建立考虑视场角约束的制导控制一体化状态空间数学模型；采用障碍Lyapunov函数、扩张状态观测器以及动态面控制相结合的控制方法。由于采用障碍Lyapunov函数、扩张状态观测器以及动态面控制相结合的控制方法，同时满足了制导精度和全捷联导引头视场角约束条件，保证了导弹制导控制过程中全捷联导引头探测的体视线角满足导引头试场约束。

下面结合附图和具体实施方式对本发明作详细说明。

附图说明

图1是本发明考虑全捷联导引头视场约束的制导控制一体化设计方法的流程图；

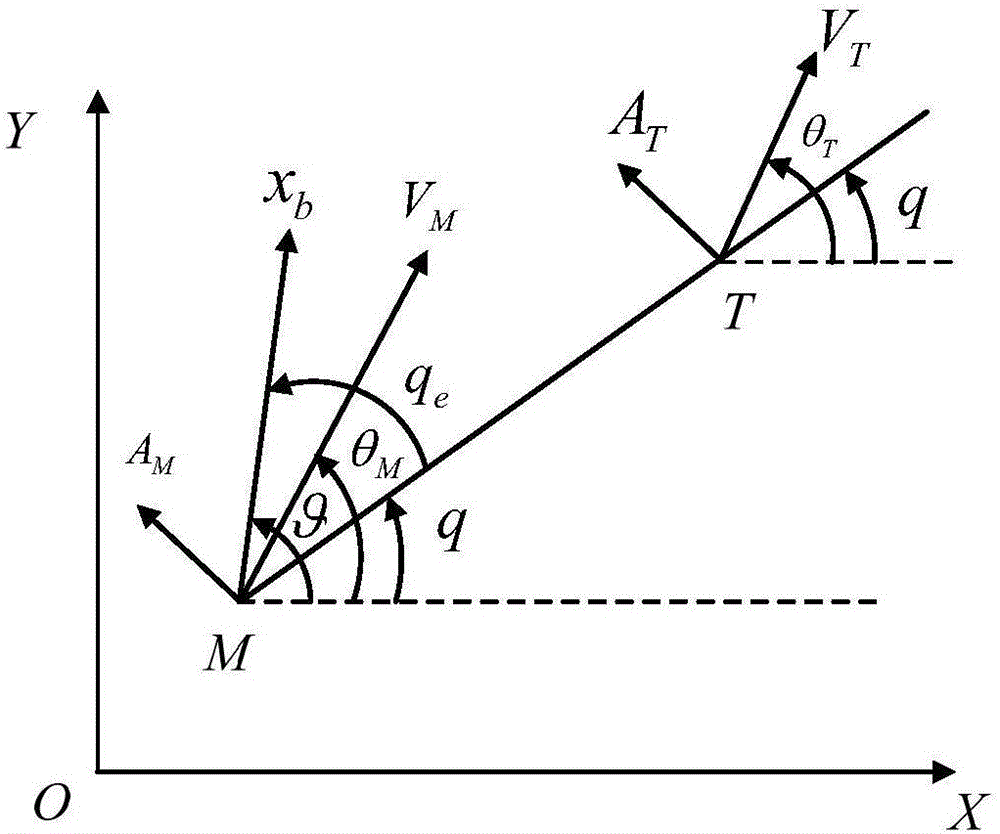
图2是导弹攻击目标过程中各个物理量信息的示意图；

图3是导弹攻击典型地面目标的弹道轨迹；

图4是导弹攻击典型地面目标过程捷联导引头测量体视线角曲线；

图5是导弹攻击典型地面目标过程惯性系视线角速度曲线；

图6是导弹攻击典型地面目标过程弹体攻角变化曲线；

图7是导弹攻击典型地面目标过程弹体俯仰角速度变化曲线。

具体实施方式

以下实施例参照图1-7。

实施例1：

本发明考虑全捷联导引头视场约束的制导控制一体化设计方法具体步骤如下：

步骤一、建立进行系统设计的状态空间模型，其由导弹纵向通道姿态控制系统模型、纵向平面内导弹-目标的相对运动模型以及全捷联导引头纵向通道视线解耦模型三部分组成。

(a)导弹纵向通道姿态控制系统模型。

其中，α是导弹的飞行攻角，ω_z是导弹的俯仰角速度，δ是导弹的俯仰舵偏角；P是导弹的发动机推力，m是导弹的质量，J_z是导弹的转动惯量，V_M是导弹的飞行速度；q是导弹的飞行动压，S是导弹的参考面积，L是导弹的参考长度；是升力系数对攻角的偏导数，是升力系数对舵偏角的偏导数，是俯仰力矩系数对攻角的偏导数，是俯仰力矩系数对舵偏角的偏导数，是俯仰阻尼力矩系数；Δ_α是攻角微分方程的不确定性，Δ_ω是角速度微分方程的不确定性。

(b)建立纵向平面内导弹-目标的相对运动模型。

其中，q是弹-目相对视线角，是弹-目相对视线角速度，是弹-目相对视线角加速度，r是弹-目相对距离，是弹-目相对速度；A_M是导弹的加速度，A_T是目标的加速度；θ_M是导弹运动的弹道角，θ_T是目标运动的弹道角；V_M是导弹的飞行速度，V_T是目标的飞行速度。

(c)建立全捷联导引头纵向通道视线解耦模型。

其中，q_ε为捷联导引头测量到的目标体视线角。

选择状态变量为建立系统状态空间模型如下：

其中，Δ₁为第一个状态方程的综合不确定性，Δ₂为第二个状态方程的综合不确定性，Δ₃为第三个状态方程的综合不确定性，Δ₄为第四个状态方程的综合不确定性；u是待设计的系统控制输入。

步骤二、采用扩张状态观测器进行系统状态以及系统干扰的在线估计，具体的设计结果如下：

其中，z₁₀是系统状态x₁的估计值，z₂₀是系统状态x₂的估计值，z₃₀是系统状态x₃的估计值，z₄₀是系统状态x₄的估计值；z₁₁是系统方程组(4)中第一个方程不确定性Δ₁的估计值，z₂₁是系统方程组(4)中第二个方程不确定性Δ₂的估计值，z₃₁是系统方程组(4)中第三个方程不确定性Δ₃的估计值，z₄₁是系统方程组(4)中第四个方程不确定性Δ₄的估计值；非线性函数fal(e_i′,α_i,σ_i)表达式如下：

步骤三、进行虚拟控制x_2d及其近似估计值的计算。

定义误差项e₁＝x₁和e₂＝x₂-x_2d，其中x_2d是待设计的x₂的虚拟控制。为了确保失调角满足要求|x₁|≤Q，Q为需要约束的视场角范围，选择障碍Lyapunov函数如下：

基于Lyapunov稳定性定理，设计虚拟控制量如下：

引入如下动态面一阶延迟进行虚拟控制量微分的估计：

步骤四、进行虚拟控制x_3d及其近似估计值的计算。

定义攻角状态的误差项e₃＝x₃-x_3d，选择新的Lyapunov函数为：

基于Lyapunov稳定性定理，设计虚拟控制量如下：

引入如下动态面一阶延迟进行虚拟控制量微分的估计：

步骤五、进行虚拟控制x_4d及其近似估计值的计算。

定义俯仰角速度状态的误差项e₄＝x₄-x_4d，选择新的Lyapunov函数为：

基于Lyapunov稳定性定理，设计虚拟控制量如下：

引入如下动态面一阶延迟进行虚拟控制量微分的估计：

步骤六、考虑视场角约束的制导控制一体化制导律设计。

选择新的Lyapunov函数为：

基于Lyapunov稳定性定理，设计虚拟控制量如下：

此时Lyapunov函数满足渐进收敛条件。

按照一体化制导控制律(17)即可对系统施加控制。

实施例2：

本实施例步骤二中扩张状态观测器取值为：

α₁＝α₂＝α₃＝α₄＝0.3,β₁₀＝β₂₀＝20,β₃₀＝β₄₀＝10

β₁₁＝β₂₁＝β₃₁＝β₄₁＝50,σ₁＝σ₂＝σ₃＝σ₄＝0.05

其他步骤及参数与实施例1相同。

实施例3：本实施例步骤三中的K₁＝10,Q＝20/57.3,τ₂＝0.025,η₁＝0.001。

其他步骤及参数与实施例1相同。

具体实施方式四：本实施例步骤四中的K₂＝5,τ₃＝0.01,η₂＝0.001。

其他步骤及参数与实施例1相同。

具体实施方式五：本实施例步骤五中的K₃＝5,τ₄＝0.01,η₃＝0.001。

其他步骤及参数与实施例1相同。

具体实施方式六：本实施例步骤六中的K₄＝5,η₄＝0.001。

其他步骤及参数与实施例1相同。

应用实施例：

参照图2，以全捷联导弹攻击空中悬停无人机为例进行方法的实施说明。其中，XOY为地面惯性系；M代表导弹位置，T代表目标点位置；矢量Mx_b表征弹体轴向，MV_M表征导弹速度矢量，MA_M表征导弹加速度矢量，MT表征弹目矢量；Mx_b和地面系OX轴夹角是弹体俯仰角，MV_M和地面系OX轴夹角θ是导弹弹道角，MT和地面系OX轴夹角q为弹-目视线角；Mx_b和MT夹角q_e为捷联导引头测量的体视线角。

给定初始仿真场景为：导弹初始坐标为(0,5000)，目标坐标为(12000,21000)；V_M,V_T分别为导弹和目标的速度取值为680m/s和0m/s，θ_M,θ_T分别为导弹和目标的弹道角度，分别取值为30°和0°；导弹初始俯仰角速度为0.1°/s；参考文献“Adaptive block dynamic surface control for integrated missile guidance and control，Chinese Journal of Aerospace，航空学报英文版，2013,Vol.26(3),p741-751”所公开的导弹参数如下：

m＝1200,J_z＝5600,S＝0.42,L＝0.68

扩张状态观测器及控制参数取值参考具体实施方式部分，仿真结束条件为弹目相对距离小于0.5m。

图3给出了导弹攻击典型空中悬停目标的弹道轨迹，可以看出整个攻击过程弹道较为平缓，由此说明对导弹的过载要求较低。

图4给出了导弹攻击典型空中悬停目标过程中捷联导引头测量体视线角曲线，可以看出，在障碍Lyapunov函数的作用下体视线角保持渐进收敛状态，从初始-4°收敛至零度附近，确保目标始终处于视场内。

图5给出了导弹攻击典型空中悬停目标过程中惯性系下的弹目视线角速度曲线，可以看出整个攻击过程视线角速度始终保持在零附近的小邻域内，具体到-0.3°以内，说明该方法很好地零化了视线角速度，可以实现近似平行接近，能够从原理上保证制导精度。

图6给出了导弹攻击典型空中悬停目标过程中弹体的攻角曲线，整个攻击过程中弹体姿态角速度从初始的27°/s快速渐进收敛至零附近的小邻域，这说明在制导控制过程中弹体的姿态稳定特性较好，一方面可以提高精度，另一方面也更有利于捷联导引头工作。

图7给出了导弹攻击典型空中悬停目标过程中弹体的俯仰角速度曲线，整个攻击过程中弹体俯仰角速度始终保持在2°/s以内，这同样说明制导控制过程中弹体的姿态稳定性较好。