一种基于RBF神经网络自抗扰控制器的设计方法与流程

本发明涉及多电机同步控制技术领域，特别是涉及一种基于rbf神经网络自抗扰控制器的设计方法。

背景技术：

多电机同步控制系统广泛应用于纺织、冶金、印刷等领域。多电机同步控制系统是一个高阶、时变、非线性的系统，且张力与速度存在着严重的耦合关系，这给多电机同步控制系统带来了更严峻的考验。目前，应用于工业控制的大多为pid控制器，但pid控制器控制效果不太好，难以达到精确的解耦控制。迄今为止，解耦算法有传统解耦算法、自适应解耦算法、智能解耦算法、滑模控制、自抗扰控制器(adrc)等，各解耦算法优势不同，应用层面也有所不同。adrc因其不依赖于精确数学的模型而广泛应用于复杂系统中。adrc虽优势众多，但其算法复杂、参数多，即使adrc的部分参数可通过查询文献资料获得，但很多参数大都是依靠经验试凑法，如误差反馈增益、补偿因子等方法获得，费时费力，控制系统扰动因素多，无法实现参数的实时调节，很难得到最优参数。近几年，逐渐有人提出了智能参数调节方法，如北京理工大学周游及其导师王庆林在《性能评价方法在adrc参数整定中的应用》中提出的性能评价方法，对adrc的大部分参数进行了优化，但仍需要辨识过程传递函数和扰动传递函数，增加了对系统模型的依赖性。

技术实现要素：

针对现有技术中存在不足，本发明提供了一种基于rbf神经网络自抗扰控制器的设计方法，通过优化自抗扰控制器adrc，并将rbf神经网络和优化后的自抗扰控制器adrc结合运用，实现对系统参数的实时调试。本发明是通过以下技术手段实现上述技术目的的。

一种基于rbf神经网络自抗扰控制器的设计方法，其特征在于，包括如下步骤：

步骤1：搭建三电机同步系统的物理模型，检测电机a的速度信号ωr1、电机a与电机b之间的张力信号f12以及电机b与电机c之间的张力信号f23；

步骤2：选择自抗扰控制器adrc对速度和张力进行解耦控制，并对自抗扰控制器adrc进行优化；

步骤3：确定优化后的adrc需调试参数n,为反馈控制律比例系数kp以及补偿因子b0；

步骤4：将一个两个输入层五个隐含层一个输出层的2-5-1结构的rbf神经网络与优化后的adrc结合，设计一个参数调节器；

步骤5：用参数调节器中的rbf神经网络跟踪速度信号ωr1、张力信号f12以及张力信号f23，得到跟踪信号，通过梯度下降算法得到优化后的adrc需调试参数的调整信息，从而实现需调试参数的实时自调节。

所述步骤2中对自抗扰控制器adrc进行优化的公式为：

e＝z1-y

z1＝z1+h(z2-β01e+b0u)

z2＝z2+h(-β02fal(e,α,δ))

e1＝v-z1

u0＝kpe1

其中，e为观测误差；z1为y的观测信号；y为三电机同步系统的速度信号或张力信号实际值，即速度信号ωr1、张力信号f12以及张力信号f23；z2为三电机同步系统总扰动的观测值；h为三电机同步系统的采样周期值；b0为补偿因子；β01，β02为状态误差反馈增益；fal(e,α,δ)为幂次函数；α为自抗扰控制器adrc的非线性因子；δ为幂次函数的线性区间；e1为状态误差信号；v为三电机同步系统的速度信号或张力信号给定信号，即ωr1^*、f12^*、f23^*；kp为自抗扰控制器adrc的反馈控制律比例系数；u为实际控制量；u0为误差反馈控制量；

其中，fal(e,α,δ)非线性函数表达式为：

所述梯度下降算法为：

步骤a：设定指标函数e(k)；

步骤b：调节优化后的adrc需调试参数，使k时刻的三电机同步系统的速度信号或张力信号的实际值y(k)逼近k时刻的三电机同步系统的速度信号或张力信号的给定信号v(k)，根据梯度下降算法，得需调试参数n的增量δn(k)；

步骤c：用y(k)的跟踪值ym(k)代替y(k)，得到δn(k)：

步骤d：通过运算得到k时刻时调整后的需调试参数n。

所述步骤a中的指标函数e(k)为，其中，v(k)为k时刻的三电机同步系统的速度信号或张力信号的给定信号；y(k)为k时刻的三电机同步系统的速度信号或张力信号的实际值，e(k)为k时刻v(k)与y(k)的差值；

步骤b中需调试参数n的增量δn(k)的计算公式为

其中，η为梯度下降算法的步长；

步骤d中调整后的需调试参数n的运算方法为，n(k)＝n(k-1)+δn(k)。

本发明的有益效果在于：

1.对一阶adrc进行了优化，并与rbf神经网络结合来实现需调试参数的实时自调节功能，省时省力，与未进行改变的一阶adrc相比，在很大程度上减少了超调量，甚至实现了无超调调节，减少了调节时间和稳态偏差。

2.该设计方法的运用使得三电机同步系统的电机速度和电机间皮带的张力可以独立控制，达到了很好的解耦控制效果，同时可以看出该方法在调试需调试参数方面优势，可实时调整优化后的自抗扰控制器adrc的需调试参数，减少了所需的人力和时间，使三电机同步系统能很快进入稳态，其动态性能和稳定性也得到很大的提高，增强了三电机同步系统的自适应性和鲁棒性，具有实际应用效果。

附图说明

图1为本发明三电机同步系统的物理模型。

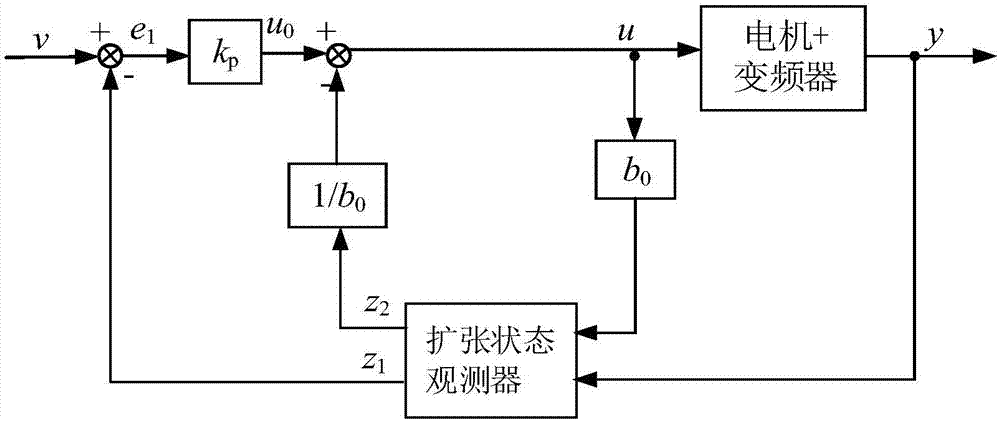
图2为本发明优化后的一阶adrc。

图3为本发明优化后的adrc与rbf神经网络结合后的参数调节器的控制图。

图4为本发明三电机同步系统的控制策略框图。

图5为本发明三电机同步系统的实验平台图。

具体实施方式

下面结合附图以及具体实施例对本发明作进一步的说明，但本发明的保护范围并不限于此。

如图1所示三电机同步系统的物理模型，三台变频器，变频器a、变频器b、变频器c分别控制三台异步电机，电机a、电机b、电机c的转速，电机a、电机b、电机c分别驱动滚筒1、滚筒2、滚筒3运转，滚筒1、滚筒2、滚筒3的半径分别为r1、r2、r3通过一条皮带相连，通过浮动辊1和浮动辊2的张紧作用分别产生皮带张力信号f12和f23。根据数学建模得到的三电机同步系统的物理模型可知，张力信号f12和f23分别与电机a和电机b之间的速度差以及电机b和电机c之间的速度差成正比，张力信号f12和f23与速度差之间存在着耦合关系。

如图5所示，pc机作为上位机，里面装有视窗控制中心wincc组态软件，利用wincc组态软件来实现系统的实时监控。西门子s7-300plc作为主控单元，并通过profinet方式与上位机进行通讯，完成程序的下载调试等功能，plc与三台西门子变频器采用profibus-dp通讯方式，实现主从站通讯，分别控制三台异步电机a、电机b和电机c，光电编码器和压力传感器。plc带有对光电编码器发出的脉冲计数的高速计数器模块fm350-1，fm350-1对光电编码器在一个采样周期内发出的脉冲进行计数，通过公式进行转速换算，其中ω为异步电机的电气角速度，单位为rad/s；n为异步电机的转速，单位为r/min；t为采样周期；c为在时间t内的计数器所计的脉冲数；e为光电编码器每转发出的脉冲数，即e＝2048。使用压力传感器采集张力信号f12和f23，且将采集的信号送入模拟量模块sm335，数字量模块sm321用于设置控制电机启停按钮。

一种基于rbf神经网络自抗扰控制器的设计方法，其特征在于，包括如下步骤：

步骤1：搭建三电机同步系统的物理模型，检测电机a的速度信号ωr1、电机a与电机b之间的张力信号f12以及电机b与电机c之间的张力信号f23；

步骤2：选择adrc对速度和张力进行解耦控制，并对自抗扰控制器adrc进行优化；

步骤3：确定优化后的adrc需调试参数n，为反馈控制律比例系数kp以及补偿因子b0；

步骤4：将rbf神经网络，一个两个输入层五个隐含层一个输出层的2-5-1结构的rbf神经网络与优化后的adrc结合，设计一个如图3所示的参数调节器；

步骤5：用参数调节器中的rbf神经网络跟踪速度信号ωr1、张力信号f12以及张力信号f23，得到跟踪信号，通过运算，即梯度下降算法，得到优化后的adrc需调试参数的调整信息，从而实现需调试参数的自调节。

如图2所示，所述步骤2中对自抗扰控制器adrc进行优化的公式为：

e＝z1-y

z1＝z1+h(z2-β01e+b0u)

z2＝z2+h(-β02fal(e,α,δ))

e1＝v-z1

u0＝kpe1

其中，e为观测误差；z1为y的观测信号；y为三电机同步系统的速度信号或张力信号的实际值，即速度信号ωr1、张力信号f12以及张力信号f23；z2为三电机同步系统总扰动的观测值；h为三电机同步系统的采样周期值；b0为补偿因子；β01，β02为状态误差反馈增益；fal(e,α,δ)为幂次函数；α为自抗扰控制器adrc的非线性因子；δ为幂次函数的线性区间；e1为状态误差信号；v为三电机同步系统的速度信号或张力信号的给定信号，即ωr1^*、f12^*、f23^*；kp为自抗扰控制器adrc的反馈控制律比例系数；u为实际控制量；u0为误差反馈控制量；

其中，fal(e,α,δ)非线性函数表达式为：

所述梯度下降算法为：

步骤a：设定指标函数e(k)；

步骤b：调节优化后的adrc需调试参数，使k时刻的三电机同步系统的速度信号或张力信号的实际值y(k)逼近k时刻的三电机同步系统的速度信号给定信号v(k)，根据梯度下降算法，得需调试参数n的增量δn(k)；

步骤c：用y(k)的跟踪值ym(k)代替y(k)，得到δn(k)：

步骤d：通过运算得到k时刻时调整后的需调试参数n。

所述步骤a中的指标函数e(k)为，其中，v(k)为k时刻的三电机同步系统的速度信号或张力信号的给定信号；y(k)为k时刻的三电机同步系统的速度信号或张力信号的实际值，e(k)为k时刻v(k)与y(k)的差值；

步骤b中需调试参数n的增量δn(k)的计算公式为

其中，η为梯度下降算法的步长；

步骤d中调整后的需调试参数n的运算方法为，n(k)＝n(k-1)+δn(k)。

三电机同步系统遵循主从控制模式，如图4所示的三电机同步系统的结构框图，该系统是一个三输入三输出的系统，三输入分别为电机a的速度信号给定值ωr1^*以及电机a、电机b间的张力信号给定值f12^*和电机b、电机c间的张力信号给定值f23^*，而三输出则分别为这三个量的实际值ωr1、f12和f23。电机a是电机b的主动电机，电机b是电机c的主动电机，电机c是从动电机。根据数学建模得到的三电机同步系统的物理模型可知，张力的大小很大程度取决于皮带连接着的两台电机的转速差。控制三台电机转速的三台变频器，可以视为该系统的“执行器”，所以控制电机a、电机b间的张力主要是在确定电机a速度的基础上控制电机b的速度。控制电机b、电机c间的张力，主要是在电机b的转速确定之后，控制电机c转速。根据图4可知，将实际速度信号值ωr1和电机a速度信号给定值ωr1^*送入所设计的优化后的一阶adrc1中获得电机a的控制信号ω1^*；将实际张力信号值f12与给定张力信号值f12^*送入优化后的一阶adrc2中，从而获得一个速度增量值δω2^*，用电机a的控制信号减去速度增量值δω2^*可得电机b的控制信号ω2^*；将实际张力信号值f23与给定张力信号值f23^*送入优化后的一阶adrc3中，获得一个速度增量值δω3^*，用电机b的控制信号减去增量值δω3^*可得电机c的控制信号ω3^*。在此过程中用rbf神经网络去跟踪电机a的速度信号，从而去调节优化后的一阶adrc1的参数kp1、优化后的一阶adrc2的参数kp2、b02以及优化后的一阶adrc3的参数kp3，并将其调节后的参数返回给优化后的adrc1、adrc2、adrc3中，从而实现实时调节需调试参数。

所述实施例为本发明的优选的实施方式，但本发明并不限于上述实施方式，在不背离本发明的实质内容的情况下，本领域技术人员能够做出的任何显而易见的改进、替换或变型均属于本发明的保护范围。