二自由度内模PID控制器参数整定方法与流程

本发明涉及控制器参数整定技术领域，尤其是涉及二自由度内模PID控制器的参数整定方法。

背景技术：

PID控制器由于结构简单、可靠性高而被广泛应用在多种控制领域，但对于船舶、潜艇等大惯性时滞的被控对象，仅采用PID控制往往不能取得满意的控制效果。将内模控制与PID控制相结合形成内模PID控制器，能够大幅度改善被控对象中时滞环节带来的不良影响，且控制器的参数整定更加简便。常规PID控制器和内模PID控制器都为单自由度控制器，只有一组调节参数，控制器的参数需要根据系统的抗干扰性和目标值跟踪特性进行折中选择，不能使系统获得最佳性能。在单自由度内模PID控制器的基础上串联一个滤波环节就可以构成二自由度内模PID控制器，使控制器含有两组可独立调节系统的抗干扰性和目标值跟踪特性的参数，大大提高了系统的控制效果，但增加了滤波环节也使得控制器的参数数量更多，参数整定过程更加复杂。目前，仍没有十分完整、有效的二自由度内模PID控制器的参数整定方法，尤其对串联的滤波环节中滤波参数的选择主要还是依赖于设计人员的经验，并且控制器一般采用固定的参数，也使其应用在被控对象参数随运行环境、工况变化而变化的系统中难以取得优越的控制效果。

技术实现要素：

针对上述凭借设计人员经验选取控制器参数以及采用固定的控制器参数难以使系统获得优越性能的缺陷，申请人进行研究及改进，提供一种二自由度内模PID控制器参数整定方法。

为了解决上述问题，本发明采用如下方案：

对于被控对象为惯性时滞环节，其传递函数可以表示为：

其中，K_m是增益系数；L_m是时滞常数；T_mi为惯性时间常数；n为系统阶数。对于式(1)中的被控对象，采用二自由度内模PID控制器为：

其中，λ₁和λ₂为待整定的控制器参数。一种二自由度内模PID控制器参数整定方法，其特征包括以下步骤：

步骤I：在被控对象每个参数变化范围内，各列出若干个典型值，组合形成多组被控对象参数；

步骤II：离线状态下，在Matlab中编写循环语句，循环次数等于步骤I中被控对象参数的数量。单次循环中完成两步操作：①改变被控对象参数，同时根据给定的最大灵敏度M_S重新整定λ₂：

②再采用遗传算法，以系统阶跃响应下的ITAE指标为目标函数，对λ₁进行寻优。所有次循环结束后，得到被控对象取不同组参数所分别对应最优的λ₁，并将所有组的被控对象参数及每组参数对应最优的λ₁保存进样本库；

步骤III：构建三层BP神经网络，神经网络的输入为被控对象的参数，输出为λ₁。离线状态下，在MATLAB中采用步骤II中得到的样本对神经网络的权值进行训练；

步骤IV：在线状态下，采用最小二乘法对被控对象参数进行实时辨识，得到被控对象的参数，再结合式(3)整定C₂(s)中的λ₂；

步骤V：在线状态下，将辨识得到的被控对象参数作为神经网络的输入，由于神经网络具有一定的泛化能力，此时λ₁取神经网络的输出值，可使系统具有优越ITAE指标。

由以上方案可以看出，本发明的二自由度内模PID控制器参数整定方法，首先在离线状态下通过循环改变被控对象的参数，并采用遗传算法得到每组被控对象参数对应最优的λ₁，作为神经网络的训练样本；再在在线状态下根据最小二乘法对被控对象参数进行辨识，根据辨识得到被控对象的参数，分别采用式(3)和训练后的神经网络对λ2和λ1进行整定。

本发明的技术效果在于：

1、样本库中λ1的获取是通过遗传算法寻优得到，此时的λ1可使系统的ITAE指标达到最优，避免了人工经验选取参数的缺陷；

2、考虑被控对象参数在实际运行中发生的变化，根据辨识得到被控对象的参数对λ2和λ1进行在线整定，克服了采用固定的控制器参数导致控制效果不理想问题；

3、控制器的参数λ1采用训练后的神经网络进行整定，其过程表现为简单的四则运算，编程实现容易，实时性和实用性都较强。

附图说明

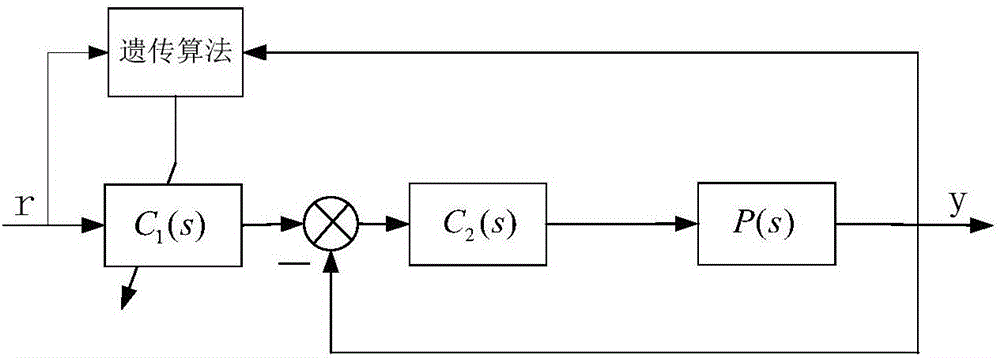
图1为本发明采用二自由度内模PID控制器的控制系统结构框图

图2为本发明采用遗传算法优化λ1的原理框图

图3为本发明样本库获取的流程图

图4为本发明三层BP神经网络结构图

图5为本发明二自由度内模PID控制器参数在线整定原理框。

具体实施方式

下面结合附图对本发明的具体实施方式作进一步说明。

本实施例应用本发明方法对系统中被控对象为二阶惯性时滞环节的二自由度内模PID控制器进行参数整定。设系统中被控对象的传递函数为：

其中，K_m是增益系数；L_m是时滞常数；T_m1，T_m2为惯性时间常数。

图1为采用二自由度内模PID控制器的控制系统结构框图。图1中的C₁(s)和C₂(s)为二自由度内模PID控制器，其传递函数为：

其中，λ₁和λ₂为待整定的控制器参数。

采用本发明方法对式(2)中二自由度内模PID控制器进行参数整定，其特征包括以下步骤：

步骤I：假设被控对象的参数K_m、L_m、T_m1、T_m2的变化范围分别为[K_mmin,K_mmax]、[L_mmin,L_mmax]、[T_m1min,T_m1max]、[T_m2min,T_m2max]，在每组参数变化范围内分别等分出o、p、q、h个值，将这些值组合形成M组不重复的被控对象参数，M＝o*p*q*h；

步骤II：离线状态下，在matlab中编写循环语句，循环次数为M。单次循环中作两步操作：①在步骤I中产生的M组被控对象参数中，按顺序取一组新的参数作为被控对象参数，最大灵敏度M_S取1.6，根据给定的最大灵敏度重新整定λ₂：

②采用遗传算法对λ₁进行寻优，λ₁的范围取[λ₂，10λ₂]，遗传算法以系统阶跃响应下的ITAE指标为目标函数，取适应度函数为

遗传算法经过参数初始化、种群初始化、遗传算子操作、新种群生成、终止条件判断等执行结束后产生该组被控对象参数所对应最优的λ₁，遗传算法优化λ₁的原理框图见图2。M次循环结束后，得到与M组被控对象参数对应的M个最优的λ₁，将M组被控对象参数和M个最优的λ₁对应组合形成M个样本，保存为样本库。样本库获取的流程图见图3；

步骤III：构建三层BP神经网络，神经网络的输入节点数取4、隐含层节点数取4，输出层节点数取1，神经网络结构图见图4。离线状态下，在MATLAB中采用步骤II中得到的M个样本对神经网络的权值进行训练；

步骤IV：在线状态下，采用最小二乘法辨识得到被控对象的参数为K_mo、L_mo、T_m1o、T_m2o，再结合式(3)整定C₂(s)中的λ₂，得到λ₂＝0.9665L_mo；

步骤V：将辨识得到的K_mo、L_mo、T_m1o、T_m2o作为训练后神经网络的输入，由于神经网络具有一定的泛化能力，此时神经网络的输出值即为λ₁的整定值。

以上内容是结合具体实施方式对本发明所作的进一步详细说明，不能认定本发明的具体实施只局限于这些说明。对于本发明所属技术领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干简单推演或替换，都应当视为属于本发明的保护范围。