一种基于自适应双层滑模的遥操作系统快速力估计方法与流程

本发明涉及遥操作机器人外力观测技术领域，尤其是一种基于自适应双层滑模的遥操作系统快速力估计方法。

背景技术：

遥操作系统由一名操作者操作一台本地机器人通过网络控制远程机器人完成指定工作任务。遥操作技术已经被广泛应用于空间技术，深海探索，远程医疗和极限环境中。在遥操作系统应用中如果远程机器人能将外界环境的触觉信息反馈到主机器人端，操作者的临场感将得到极大的改善。临场感技术是人机交互遥操作的核心。具有临场感的遥操作机器人系统是主从是遥控机器人的一种发展，侧重于远地环境在操作者周围的再现，这需要力传感器来实现。一方面，在实际应用中，力传感器存在惯性力的影响严重、动态频率低、维间干扰较大以及体积大等问题，而且在某些恶劣环境下不允许传感器的使用。另一方面，考虑节省传感器本身昂贵成本费用的问题。因此迫切需要提出新的快速、准确的力估计方法，从而代替遥操作机器人系统对力传感器的需求。

针对系统的不确定和外界干扰，滑模控制提供了很好的控制效果。利用自适应双层超螺旋有限时间滑模的方法设计全维状态观测器能很好的观测出系统的状态和外界干扰。自适应滑模参数的方法能随着外界干扰的大小而调整滑模参数。但是基于传统的滑模的状态观测器会因为未知的外界干扰而设置较大的滑模参数，其观测信号的准确度会受到很大影响。而且现有的大部分观测器设计方案依赖于遥操作系统机器人的速度信号即假设系统速度已知，增加了设备的成本。在实际中，通常情况下往往位置信号容易测得，而速度和外力的信号不易测得。

技术实现要素：

本发明目的在于提供一种能够获得准确速度和外力信号的基于自适应双层滑模的遥操作系统快速力估计方法。

为实现上述目的，采用了以下技术方案：本发明所述方法步骤如下：

s1、选取一个由两个3自由度机器人构成的遥操作机器人系统，在无负载情况下测量机器人连杆的质量和长度信息；根据能量平衡方程建立遥操作系统的任务空间下二阶拉格朗日系统模型；

s2、利用机器人本身的位置编码器测量机器人的位置信号，根据位置信息设计自适应双层超螺旋滑模全维观测器，并由观测到的信息得出估计的力的求法；

s3、根据不同的工作环境下不同的外力大小及外力改变情况，通过选取足够大的观测器参数以保证观测器系统稳定。

进一步的，所述步骤s1中，无负载情况下机器人的连杆的质量和长度信息可在机器人的出厂说明书中得到；根据杆的长度和质量信息分别计算出的主机器人和从机器人的惯性矩阵、哥氏力、离心力矩阵、雅可比矩阵和重力项。

进一步的，所述步骤s1中，建立遥操作系统的任务空间下二阶拉格朗日模型由以下条件得到：

根据普遍使用的机器人系统的拉格朗日动力学模型给出主从机器人系统的基于关节空间的动力学模型：

其中，m表示主机器人，s表示从机器人；qm(t),qs(t)∈rⁿ为关节位移矩阵；为关节速度矩阵；mm(qm),ms(qs)∈r^n×n为正定的惯性矩阵；为哥氏力和离心力矩阵；gm(qm),gs(qs)∈rⁿ为重力扭矩；fh∈rⁿ和fe∈rⁿ分别为人类操作者施加的力矩和环境施加的力矩；fm∈rⁿ和fs∈rⁿ为提供的控制扭矩；

把主机器人关节的位移和速度写成下面的形式

可以得到

相对应，定义从机器人的位移和速度如下

可以得到

进一步的，所述步骤s2中，利用机器人自带的编码器得到关节位置信息，设计全维状态观测器，观测器形式如下

其中，和中的第i个元素有如下形式

其中，分别为向量的第i个元素；定义的形式如下

增益αm(t),βm(t)的第i个元素有如下形式

其中，为正常数，且为向量αm0,βm0的第i个元素；

基于公式(3)，(6)，得到误差系统如下

其中，

由于误差系统(10)是有限时间稳定的；所以由李普希兹条件可得

fm(t)＝-mm^-1(qm1)fh(11)

由于误差项有限时间趋近于零点，所以可得为向量fm(t)的第i个元素；

双层快速调节的方法建立在“等效控制”方法基础上；由于高频切换的信号很难被利用，等效输出作为一种滤波的手段来消除高频切换的部分；采用如下滤波形式

其中，向量其中为向量的等效输出，变量为向量的第i个元素，变量为的导数，变量为向量的第i个元素，为一个极小的正常数且为向量τm的第i个元素；

双层快速调节的方法：

首先定义一个变量δm(t)∈rⁿ，δ(t)的第i个元素的形式如下

其中，为向量am,βm0的第i个元素，为常数且满足为一个极小的正常数且为向量εm的第i个元素；向量am,εm代表了安全范围并且增加了稳定的保守性；定义变量如下

其中，变量为向量lm(t)∈rⁿ的第i个元素；为正常数且为向量lm0的第i个元素；的导数满足下面式子

其中，变量为向量ρm(t)的第i个元素；变量定义如下

其中，为正常数且为向量rm0的第i个元素；变量为向量rm(t)∈rⁿ的第i个元素；变量的导数满足

其中，正常数为向量γm的第i个元素；

式(13)—(17)即为双层快速调节的方法；首先，第一层保证主机器人观测器调整参数即这是差分系统(10)收敛必须满足的条件；其次，第二层使得变量改变的速率决定于时变参数的变化，提高了调整速率；

相应的，从状态观测器给出如下

其中，

其中的从机器人的变量含义与上面主机器人变量含义相对应；

基于公式(5)，(19)，得到误差系统如下

其中，

从端机器人的等效输出形式为

对应的，从端机器人观测器双层快速调节方法给出如下

其中从端观测器双层快速调节方法的变量的定义与上述主端双层快速调节方法的变量含义相对应。

与现有技术相比，本发明具有如下优点：

1、不但能实现对系统速度以及外力的有限时间快速、精确估计，还能有效解决抖动问题。

2、滑模思想的引入使得观测器对外界干扰不敏感，增强了闭环系统的鲁棒性能。

3、利用自适应的思想，能更准确的完成对外力的估计；而双层的思想，则能更快的完成对外力的估计。通过选取合适的李雅普诺夫函数对观测器的稳定性进行了证明。

附图说明

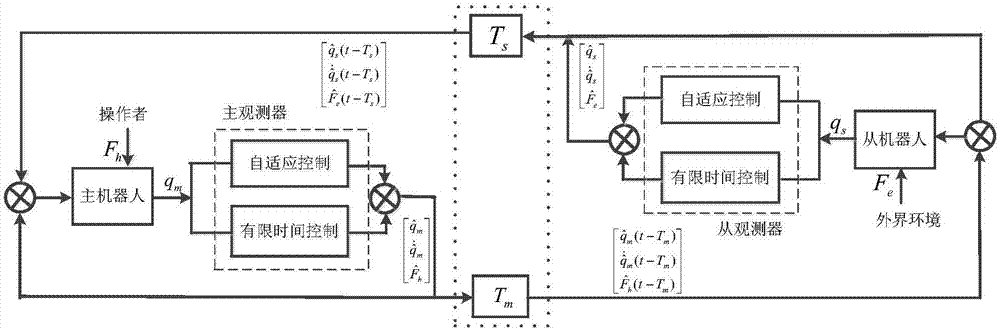
图1为遥操作机器人系统的结构框图。

图2为本发明控制系统结构图。

具体实施方式

下面结合附图对本发明做进一步说明：

如图1所示，遥操作系统主要由操作者、主机器人、网络传输通道、从机器人和外界环境组成。操作者在本地对主机器人进行操作，其相关运动信息通过网络传输至从机器人，从机器人按照主机器人的运动信息进行同步运动，并将与环境相接触得到的信息反馈回主机器人。使用观测器对主、从机器人进行观测，分别得到操作者和外界环境对主、从机器人施加的外力信息。

如图2所示，本发明方法包括以下步骤：

s1.选取一个由两个3自由度机器人构成的遥操作机器人系统，在无负载情况下测量机器人连杆的质量和长度信息。进一步根据能量平衡方程建立遥操作系统的任务空间下二阶拉格朗日系统模型。

s2.利用机器人本身的位置编码器测量机器人的位置信号，根据位置信息设计自适应双层超螺旋滑模全维观测器，并由观测到的信息得出估计的力的求法；

s3.根据不同的工作环境下不同的外力大小及外力改变情况，确定具体的观测器参数。

对于机械臂系统，所述步骤s1中，无负载情况下机器人连杆的质量和长度信息可在机器人的出厂说明书中得到。根据连杆的长度和质量信息分别计算出的主机器人和从机器人的惯性矩阵、哥氏力、离心力矩阵、雅可比矩阵和重力项。

建立遥操作系统的任务空间下二阶拉格朗日系统模型由以下条件得到。根据普遍使用的机器人系统的拉格朗日动力学模型给出主从机器人系统的基于关节空间的动力学模型

其中，m表示主机器人，s表示从机器人；qm(t),qs(t)∈rⁿ为关节位移矩阵；为关节速度矩阵；mm(qm),ms(qs)∈r^n×n为正定的惯性矩阵；为哥氏力和离心力矩阵；gm(qm),gs(qs)∈rⁿ为重力扭矩；fh∈rⁿ和fe∈rⁿ分别为人类操作者施加的力矩和环境施加的力矩；fm∈rⁿ和fs∈rⁿ为提供的控制扭矩。

把主机器人关节的位移和速度写成下面的形式

可以得到

相对应，定义从机器人的位移和速度如下

可以得到

优选地，所述步骤s2中，利用机器人自带的编码器得到关节位置信息，设计全维状态观测器，观测器形式如下

其中，和中的第i个元素有如下形式

其中，分别为向量的第i个元素。定义的形式如下

增益αm(t),βm(t)的第i个元素有如下形式

其中，为正常数，且为向量αm0,βm0的第i个元素。lm(t)的形式在后面的内容中给出。

基于公式(3)，(6)，得到误差系统如下

其中，

由于误差系统(10)是有限时间稳定的。所以由李普希兹条件可得

fm(t)＝-mm^-1(qm1)fh(11)由于误差项有限时间趋近于零点，所以可得为向量fm(t)的第i个元素。

双层快速调节的方法建立在“等效控制”方法基础上。由于高频切换的信号很难被利用，等效输出作为一种滤波的手段来消除高频切换的部分。我们采用如下滤波形式

其中，向量为向量的等效输出，变量为向量的第i个元素，变量为的导数，变量为向量的第i个元素，为一个极小的正常数且为向量τm的第i个元素。

下面给出双层快速调节的方法。首先定义一个变量δm(t)∈rⁿ，δ(t)的第i个元素的形式如下

其中，为向量am,βm0的第i个元素，为常数且满足为一个极小的正常数且为向量εm的第i个元素。向量am,εm代表了安全范围并且增加了稳定的保守性。定义变量如下

其中，变量为向量lm(t)∈rⁿ的第i个元素；为正常数且为向量lm0的第i个元素。的导数满足下面式子

其中，变量为向量ρm(t)的第i个元素。变量定义如下

其中，为正常数且为向量rm0的第i个元素；变量为向量rm(t)∈rⁿ的第i个元素。变量的导数满足

其中，正常数为向量γm的第i个元素。

(13)—(17)即为双层快速调节的方法。首先，第一层保证主机器人观测器调整参数即这是差分系统(10)收敛必须满足的条件。其次，第二层使得变量改变的速率决定于时变参数的变化，提高了调整速率。

相应的，从状态观测器给出如下

其中，

其中的从机器人的变量含义与上面主机器人变量含义相对应。

基于公式(5)，(19)，得到误差系统如下

其中，

从端机器人的等效输出形式为

对应的，从端机器人观测器双层快速调节方法给出如下

其中从端观测器双层快速调节方法的变量的定义与上文中主端双层快速调节方法的变量含义相对应。

以上所述的实施例仅仅是对本发明的优选实施方式进行描述，并非对本发明的范围进行限定，在不脱离本发明设计精神的前提下，本领域普通技术人员对本发明的技术方案做出的各种变形和改进，均应落入本发明权利要求书确定的保护范围内。