一种基于缺失变量建模思路的非高斯过程监测方法与流程

本发明涉及一种工业过程监测方法，尤其是涉及一种基于缺失变量建模思路的非高斯过程监测方法。
背景技术：
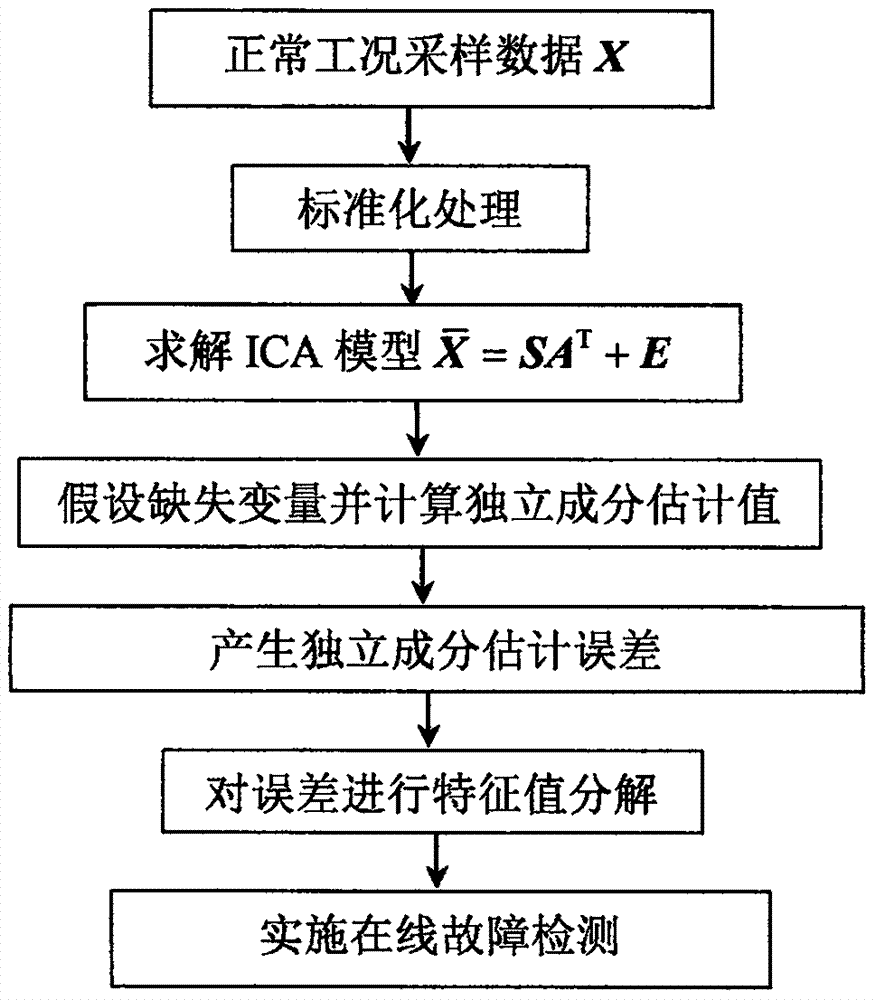
：在工业生产流程中，确保生产过程持续处于正常工况对于保证产品质量稳定性具有重要意义。因此，具备故障检测功能的过程监测模块在生产实际中必不可少，这也是学术界和工业界能一直持续不断的针对过程监测进行理论与应用研究的主要原因。从研究历程上看，过程监测从最开始的基于机理模型的故障检测方法开始，已经逐步演变成数据驱动的故障检测方法。相比于建立机理模型，数据驱动的方法实施起来更加容易，更加适合于现代大型工业过程对象。当前，工业“大数据”的趋势下也在不断地催生着新型数据驱动的过程监测方法。在这一研究领域中，多变量统计分析算法是被最广泛使用的建模方法。其中，以主成分分析(principalcomponentanalysis，pca)与独立成分分析(independentcomponentanalysis，ica)为基础的故障检测方法层出不穷，衍生出了各式各样的、能适应于不同类型工业对象的过程监测方法。一般来讲，基于pca的过程监测模型大多都假设采样数据服从近似高斯分布，从而可以方便地确定出描述正常数据变化范围的控制上限。然而，现代工业过程对象的复杂性导致采样数据不服从高斯分布。因此，传统pca方法用于故障检测时存在较为显著的故障漏报率或误报率。相比之下，ica算法可以挖掘出非高斯的独立成分信息，更适合于监测非高斯过程数据。而且，许多科研文献也都通过实例验证了基于ica的方法优越于基于pca的方法。在现有的科研与专利文献中，确定ica故障检测模型的控制限的方法主要依赖于核密度估计。从空间几何结构上看，该控制限其实定义了一个超球体的表面，所有位于超球体内部的数据点都为正常工况数据。然而，由于数据本身的非高斯性，正常数据的分布范围不可能全部填充该超球体。因此，位于超球体内部的数据点不一定都是正常数据样本。造成这一问题的因素主要源于ica模型提取的独立成分本身是非高斯的。因此，就这一点问题上基于ica的非高斯过程监测模型还需进一步的改进。值得注意的是，误差一般都服从或近似服从高斯分布。可是，误差的产生通常需要一个实际值与一个估计值，每个监测样本转换成对应的独立成分后即可当成ica模型的实际值。那么，如何产生独立成分的估计值就是最关键的一个问题。可想而知，若能产生独立成分的估计值，那么独立成分实际值与估计值之间的误差就可以获得。而且，原始不服从高斯分布的独立成分变成误差后，也就服从高斯分布了，确定相应的控制限就可以更精确地描述正常数据的分布范围。在已有的研究文献中，有部分学者在传统pca的故障检测模型中提出了缺失变量的处理方法，旨在解决生产实际中的采样数据有可能会出现数据缺失的问题。缺失变量的方法主要通过已有的pca模型，利用已测量得到的数据在不需要缺失数据的前提下可以将相对应的主成分信息估计出来。鉴于此，利用缺失变量处理的思路或许能为产生独立成分的估计值提供一条可行的解决策略。技术实现要素：本发明所要解决的主要技术问题是：如何利用缺失变量的建模思路建立一个更可靠的非高斯过程监测模型。为此，本发明提供了一种基于缺失变量建模思路的非高斯过程监测方法。该方法在传统ica模型的基础上，通过逐一假设各个测量变量缺失数据后估计出相应的独立成分。然后，以独立成分实际值与估计值之间的误差做为被监测对象，建立适当统计量实施在线过程监测。本发明解决上述技术问题所采用的技术方案为：一种基于缺失变量建模思路的非高斯过程监测方法，包括以下步骤：(1)利用采样系统收集生产过程正常运行状态下的样本数据，组成训练数据矩阵：x∈rn×m，并对x进行标准化处理，使每个测量变量的均值为0，方差为1，得到新的数据矩阵其中，n为训练样本数，m为过程测量变量数，r为实数集，rn×m表示n×m维的实数矩阵，为矩阵中第k个变量的n个测量数据，k＝1，2，…，m。(2)利用ica算法为建立ica模型，即：其中，为d个独立成分列向量组成的矩阵，w∈rm×d为分离矩阵，a∈rm×d为混合矩阵，e∈rn×m表示模型误差，上标号t表示矩阵或向量的转置。(3)假设矩阵中第k列数据缺失，其余可用列组成矩阵xk∈rn×(m-1)，并利用如下所示公式计算得到独立成分矩阵的估计值上式中，ak∈r(m-1)×d为混合矩阵a中去除第k行所得到的矩阵。(4)计算实际值s与估计值之间的误差并计算矩阵fk的协方差矩阵ck＝fktfk/(n-1)。(5)计算矩阵ck最大特征值所对应的特征向量αk∈rd×1，并置(6)判断k＜m？若是，则置k＝k+1后返回步骤(3)；若否，则执行步骤(7)。(7)调用模型参数集实施在线过程监测，具体的实施过程如下所示：①采集生产过程对象最新时刻的采样数据ynew∈r1×m，对其进行与x同样的标准化处理得到②计算样本向量所对应的独立成分向量的实际值并初始化k＝1。③假设样本向量中第k个变量数据缺失，将中其余数据组成新向量并利用公式计算得到独立成分向量的估计值④计算独立成分向量的实际值与估计值之间的误差⑤按照如下所示公式计算监测统计量qk：qk＝(fkαk)2(1)⑦判断k＜m？若是，则置k＝k+1后返回步骤③；若否，则执行步骤⑧。⑧置q＝max{q1，q2，…，qm}后，判断是否满足条件：若是，则当前样本是正常样本，生产过程处于正常工作状态并返回①继续监测下一个新样本；若否，则该样本为故障样本，生产过程进入非正常工况并触发故障警报。其中，符号max{}表示取最大值，表示自由度为1、置信度为δ的卡方分布所对应的数值。与传统方法相比，本发明方法的优势主要体现在以下两个方面：一方面，本发明方法监测的对象是独立成分的估计误差，虽然独立成分是非高斯分布的但误差本身一般服从高斯分布。可以说，本发明方法是通过缺失变量的建模思路将非高斯过程采样数据巧妙的转换成了高斯分布的误差数据，对应确定的控制限也就能对正常数据进行更精确的描述。另一方面，本发明方法通过逐一假设各个测量变量数据缺失，从而建立了与监测变量个数相等的故障检测模型。与传统基于单个ica模型的故障检测方法相比，本发明方法还发挥了多模型泛化能力强的优势。综合以上两方面优点，本发明方法是一种更为优选的非高斯过程监测方法。附图说明图1为本发明方法的实施流程图。图2为误差f1中第一列与独立成分s中第一列元素的高斯分布检验图。图3为本发明方法与传统ica方法平均故障漏报率对比图。具体实施方式下面结合附图对本发明方法进行详细的说明。如图1所示，本发明涉及一种基于缺失变量建模思路的非高斯过程监测方法，该方法的具体实施步骤如下所示：(1)利用采样系统收集生产过程正常运行状态下的样本数据，组成训练数据矩阵：x∈rn×m，并对x进行标准化处理，使每个测量变量的均值为0，方差为1，得到新的数据矩阵其中，n为训练样本数，m为过程测量变量数，r为实数集，rn×m表示n×m维的实数矩阵，为矩阵中第k个变量的n个测量数据，k＝1，2，…，m。(2)利用ica算法为建立ica模型，并初始化k＝1。建立ica模型的的实施过程如下所示：①计算的协方差矩阵其中c∈rm×m；②计算矩阵c的所有特征值和特征向量，并剔除小于0.0001的特征值及其对应的特征向量，得到特征向量矩阵p＝[p1，p2，…，pm]∈rm×m以及特征值对角矩阵d＝diag(λ1，λ2，…，λm)∈rm×m；值得注意的是，这里求解得到的特征向量p1，p2，…，pm都必须是单位长度的向量。③根据公式对进行白化处理，得到z∈rn×m，并初始化i＝1；④取列向量ci为m×m维单位矩阵中的第i列，⑤按照如下所示公式更新ci，即：ci←e{zg(citz)}-e{h(citz)}ci(2)上式(2)中，e{}表示求取期望值(即向量的平均值)，函数g和h的具体形式如下所示：g(u)＝tanh(u)(3)h(u)＝[sech(u)]2(4)上式(3)与(4)中，u为函数自变量，在这里指代citz中的元素。⑥对更新后的向量ci依次按照下式进行正交标准化处理：ci←ci/||ci||(6)⑦重复步骤⑤～⑥直至向量ci收敛，并保存向量ci；⑧判断i＜m？若是，置i＝i+1后，重复步骤④～⑧；若否，执行步骤⑨；⑨将得到的所有m个向量c1，c2，…，cm组成矩阵c＝[c1，c2，…，cm]∈rm×m，并按照如下所示公式计算分离矩阵w0∈rm×m与混合矩阵a0∈rm×m：a0＝pd1/2c(7)w0＝pd-1/2c(8)⑩计算a0中每一列向量的长度，分别记为l1，l2，…，lm，并将l1，l2，…，lm按照数值大小进行降序排列得到l1，l2，…，lm，那么保留的独立成分个数d为满足下列条件的最小值：将a0中列向量长度最大的d个列向量组成新的混合矩阵a∈rm×d，同时从w0中取出与a对应的列向量组成新分离矩阵w∈rm×d；最后得到的ica模型为其中，为d个独立成分列向量组成的矩阵，e∈rn×m表示模型误差。(3)假设矩阵中第k列数据缺失，其余可用列组成矩阵xk∈rn×(m-1)，并利用如下所示公式计算得到独立成分矩阵的估计值上式中，ak∈r(m-1)×d为混合矩阵a中去除第k行所得到的矩阵。(4)计算实际值s与估计值之间的误差并计算矩阵fk的协方差矩阵ck＝fktfk/(n-1)。(5)计算矩阵ck最大特征值所对应的特征向量αk∈rd×1，并置(6)判断k＜m？若是，则置k＝k+1后返回步骤(3)；若否，则执行步骤(7)。(7)调用模型参数集实施在线过程监测，具体的实施过程如下所示：①采集生产过程对象最新时刻的采样数据ynew∈r1×m，对其进行与x同样的标准化处理得到②计算样本向量所对应的独立成分向量的实际值并初始化k＝1。③假设样本向量中第k个变量数据缺失，将中其余数据组成新向量并利用公式计算得到独立成分向量的估计值④计算独立成分向量的实际值与估计值之间的误差⑤按照如下所示公式计算监测统计量qk：qk＝(fkαk)2(11)⑦判断k＜m？若是，则置k＝k+1后返回步骤③；若否，则执行步骤⑧。⑧置q＝max{q1，q2，…，qm}后，判断是否满足条件：若是，则当前样本是正常样本，生产过程处于正常工作状态并返回①继续监测下一个新样本；若否，则该样本为故障样本，生产过程进入非正常工况并触发故障警报。其中，符号max{}表示取最大值，表示自由度为1、置信度为δ的卡方分布所对应的数值。下面结合一个具体的工业过程的例子来说明本发明方法相对于现有方法的优越性与可靠性。该过程数据来自于美国田纳西-伊斯曼(te)化工过程实验，原型是伊斯曼化工生产车间的一个实际工艺流程。目前，te过程因其流程的复杂性，已作为一个标准实验平台被广泛用于故障检测研究。整个te过程包括22个测量变量、12个操作变量、和19个成分测量变量。所采集的数据分为22组，其中包括1组正常工况下的数据集与21组故障数据。而在这些故障数据中，有16个是已知故障类型，如冷却水入口温度或进料成分的变化、阀门粘滞、反应动力学漂移等，还有5个故障类型是未知的。为了对该过程进行监测，选取如表1所示的33个过程变量，接下来结合该te过程对本发明具体实施步骤进行详细的阐述。表1：te过程监测变量。序号变量描述序号变量描述序号变量描述1物料a流量12分离器液位23d进料阀门位置2物料d流量13分离器压力24e进料阀门位置3物料e流量14分离器塔底流量25a进料阀门位置4总进料流量15汽提塔等级26a和c进料阀门位置5循环流量16汽提塔压力27压缩机循环阀门位置6反应器进料17汽提塔底部流量28排空阀门位置7反应器压力18汽提塔温度29分离器液相阀门位置8反应器等级19汽提塔上部蒸汽30汽提塔液相阀门位置9反应器温度20压缩机功率31汽提塔蒸汽阀门位置10排空速率21反应器冷却水出口温度32反应器冷凝水流量11分离器温度22分离器冷却水出口温度33冷凝器冷却水流量(1)采集te过程对象正常工况下的过程数据，并选取960个正常数据组成矩阵x∈r960×33，对其进行标准化处理得到(2)利用ica算法为建立ica模型，即：并初始化k＝1。(3)假设矩阵中第k列数据缺失，其余可用列组成矩阵xk∈r960×32，并利用如下所示公式计算得到独立成分矩阵的估计值上式中，ak∈r32×28为混合矩阵a中去除第k行所得到的矩阵；(4)计算实际值s与估计值之间的误差并计算矩阵fk的协方差矩阵ck＝fktfk/(n-1)；由于本发明方法监测的对象为误差fk，而传统ica方法监测的是独立成分s，特对f1中第一列与独立成分矩阵s中第一列的数据进行高斯分布检验，结果显示于图2中。若所测试数据严格服从高斯分布，图2中的散点图则为一条直线。很显然，本发明方法中误差f1近似服从高斯分布，而传统ica方法中由于提取的是非高斯的独立成分，当然就不符合高斯分布。从这个对比也可以说明，本发明方法可以将非高斯的成分巧妙地转换成近似服从高斯分布的误差。这样一来，本发明方法确定的控制限就可以按照卡方分布分来获取。(5)计算矩阵ck最大特征值所对应的特征向量αk∈r28×1，并置(6)判断k＜m？若是，则置k＝k+1后返回步骤(3)；若否，则离线建模完成并实施在线故障监测；为测试本发明方法的在故障检测上的优越性，以监测te过程21种故障的平均故障检测成功率为例，对比本发明方法与传统基于ica方法的故障检测效果。该测试数据有960个样本组成，其前160个样本为正常工况下采样，后800个样本为故障工况采样。①采集生产过程对象最新时刻的采样数据ynew∈r1×33，对其进行与x同样的标准化处理得到②计算样本向量所对应的独立成分向量的实际值并初始化k＝1；③假设样本向量中第k个变量数据缺失，将中其余数据组成新向量并利用公式计算得到独立成分向量的估计值④计算独立成分向量的实际值与估计值之间的误差⑤按照如下所示公式计算监测统计量qk：qk＝(fkαk)2(2)⑦判断k＜33？若是，则置k＝k+1后返回步骤③；若否，则执行步骤⑧；⑧置q＝max{q1，q2，…，q33}后，根据条件决策故障是否发生。本发明发与传统ica方法针对te过程21种故障类型的平均故障漏报率显示于图3中，可以发现，本发明方法的平均故障漏报率明显低于传统ica方法。因此，本发明方法改进了基于ica的非高斯过程监测方法的故障检测性能。上述实施例只用来解释本发明，而不是对本发明进行限制，在本发明的精神和权利要求的保护范围内，对本发明做出的任何修改和改变，都落入本发明的保护范围内。当前第1页12