非线性抽水蓄能机组调速系统增益启发式自适应PID控制方法与流程

本发明属于水力发电机组控制优化领域，更具体地，涉及一种非线性抽水蓄能机组调速系统启发式增益自适应pid控制方法。

背景技术：

作为一种清洁可再生能源，抽水蓄能机组以其启停快速、运行灵活、能快速反应电网频率负荷变化等独特优势，在维护电网安全稳定运行中发挥着重要作用。然而，由于抽水蓄能机组本身的可逆性设计，低比转速水泵水轮机将不可避免的存在“s”特性区和水泵驼峰区，导致低水头水轮机工况起动并网困难，甩负荷工况机组剧烈震动等问题。因此，抽水蓄能机组的稳定性问题比传统水轮发电机组更加严峻。

控制理论作为提高系统稳定性最经济有效的重要手段之一，被应用于加强抽水蓄能机组安全稳定运行。传统的pid控制器由于结构简单、易于实现，参数较少、容易整定而被广泛使用。然而，传统pid控制器参数固定难以满足抽水蓄能机组因水头、出力等因素变化引起的控制要求。因此，抽水蓄能机组调速系统新型控制规律的研究备受关注。

基于现有的研究，抽水蓄能机组调速系统控制方法主要存在以下不足：1)非线性抽水蓄能机组调速系统模型的pid控制方法中，固定的控制增益参数难以适应水头变化和工况转换的调节要求；2)抽水蓄能机组调速系统简化模型的非线性控制方法中，简化模型难以表征调速系统的水击与强非线性，这与工程实际情况存在一定差距，因此，较难获得具有工程应用价值的准确控制参数；3)现有非线性控制器往往结构复杂，在一定程度上忽视了“简单性优先”原则，较难应用于工程实际。

因此，需要开发一种适用于非线性抽水蓄能机组调速系统新型控制方法，该方法要求结构简单、易于实现，能满足实际电站中调速器实时采样需求，并且该方法在充分适应抽水蓄能机组调速系统各模块耦合非线性同时，可以改善传统控制方法在不同水头条件下机组的动态品质。

技术实现要素：

针对现有技术的缺陷或改进需求，本发明目的在于提出一种适用于非线性抽水蓄能机组调速系统的启发式增益自适应pid控制方法。本发明的非线性抽水蓄能机组调速系统的启发式增益自适应pid控制方法既能充分适应调速系统各模块的耦合非线性，又能改善传统控制方法在不同水头尤其是低水头条件下机组的控制品质。

为了实现上述目的，本发明提供了一种非线性抽水蓄能机组调速系统启发式增益自适应pid控制方法，包括如下步骤：

步骤1：受电容间场强作用力平衡原理启发，根据专家控制经验(所述专家控制经验包括：大误差时大比例弱积分，用于加快系统响应速度；小误差时小比例强积分，用于保证稳态精度)，建立适用于非线性抽水蓄能机组调速系统的hgs-npid控制器。所述hgs-npid控制器的控制增益可根据误差及误差变化率在线自动调整，以实现自适应变增益变结构控制。

步骤2：建立非线性抽水蓄能机组调速系统精细化模型，所述调速系统精细化模型包括调速器模型、基于特征线法的有压过水系统模型、基于改进suter变换的水泵水轮机插值模型以及发电机及负载模型，其中，调速器模型由hgs-npid控制器及两级电液随动装置共同构成。

两级电液随动装置、有压过水系统、水泵水轮机、发电机及负载构成被控制的对象，由hgs-npid控制器进行调节控制。

以水轮机工况为例，hgs-npid控制器根据机组转速偏差产生调节控制信号驱动两级电液随动装置，改变水泵水轮机的导叶开度，水泵水轮机进口流量随之发生改变；在导叶开度改变瞬间，有压过水系统中往往发生水锤现象，导致蜗壳压力发生变化；水泵水轮机进口流量和蜗壳压力的变化，会使水轮机工况主动力矩发生改变，从而使水轮机方向力矩与发电机的负载阻力矩产生差值，发电机转速随之发生变化，转速改变自然地同步调节了频率大小，达到调节机组频率的目的。

步骤3：建立上述非线性抽水蓄能机组调速系统精细化模型的hgs-npid控制参数优化的多目标函数，采用时间误差平方积分itse指标和误差平方积分ise指标作为hgs-npid控制参数优化的多目标函数，分别定义为：

itse指标：

ise指标：

式中，c(k)为频率给定值序列；x(k)为机组转速响应序列，是非线性抽水蓄能机组调速系统输出，受控制参数影响；t(k)为时间序列；ns为采样点数；k为仿真步数；优化向量θ为[e0、m、kpmax、b、kimax、kda、kdb]，其中，e0为误差最大值、m为比例增益调节系数、kpmax为比例增益幅值、b为积分增益调节系数、kimax为积分增益幅值、kda和kdb均为微分增益调节系数。

步骤4：运用多目标智能优化算法求解步骤3中hgs-npid控制参数优化的多目标函数，获得最优的hgs-npid控制参数，包括误差最大值e0、比例增益幅值kpmax、比例增益调节系数m、积分增益调节系数b、积分增益幅值kimax、微分增益调节系数kda及kdb。

进一步，所述步骤1中hgs-npid控制器以位置型并联pid结构为基础，由比例、积分、微分三个环节组成，具体的，

1)比例环节的设计受电容间场强作用力平衡原理启发，即处于两正极板间任意位置的正电荷，会在电场力作用下运动，最终稳定于平衡位置。正电荷在任意坐标位置e所受电场力为u(e)：

式中，两电极距坐标原点位置为±e0，电极电压为u0。依据比例增益对误差信号的控制作用与电场力对电荷作用的相似性，将电荷位置坐标参量e看作控制误差量，依据上式构造比例增益关于误差e的自适应函数kp(e)如下：

其中，e0为误差最大值，e为控制误差，kpmax为比例增益幅值。当误差e＝e0时,kp＝kpmax，比例环节作用最强；当e＝0时,kp＝0，比例环节消失。比例增益调节系数m可以调节函数曲率，能提高比例增益对误差变化的适应性。

2)积分环节设计引入变速积分思想，采用二次非线性函数对积分项进行改进，使积分项的累积速度与控制误差大小相对应。积分增益自适应函数ki(e)表达式如下：

其中,kimax为积分增益幅值，b为积分增益调节系数，其可调节积分增益变化速度。当|e|＝0时，积分动作达最高速，ki(e)＝kimax；当|e|＝e0时，为避免超调不再对当前误差进行累加，ki(e)＝0。

3)微分环节增益自适应函数kd(e,δe)考虑误差e及误差变化率δe，表达式如下：

kd(e,δe)＝kda*exp(e*sign(δe))+kdb

其中，kda、kdb为微分增益调节系数。

综上所述，hgs-npid控制器结构表达式如下：

upid为一个连续方程，将该连续方程离散化得下式：

ek＝xk-xo

δek＝(ek-ek-1)/ts

ud,k＝kd(ek,δek)/(td+ts)*δek+td/(td+ts)*ud,k-1

其中，upid,k为控制器输出、k为仿真步数、xo为机组转速给定、xk为第k次仿真机组转速响应、ek-1为第k-1次仿真的控制误差、ek为第k次仿真的控制误差、δek为第k次仿真的控制误差变化率、ud,k-1为第k-1次仿真积分环节控制输出、ud,k为第k次仿真积分环节控制输出、ts为采样时间间隔、td为积分时间常数，j为0、1···、k。

hgs-npid控制器中误差最大值e0、比例增益调节系数m、比例增益幅值kpmax、积分增益调节系数b、积分增益幅值kimax、微分增益调节系数kda和kdb为需要优化的控制参数。

进一步的，所述步骤2中，非线性抽水蓄能机组调速系统精细化建模包括以下子步骤：

1)基于特征线法建立有压过水系统模型，该模型不仅考虑了复杂水击、管道摩阻损失，还计及调压井等边界特性，精确度较高。正负波速±c情况下的特征线方程如下：

其中：

cp＝qa+caha-cfqa|qa|

cn＝qb-cahb-cfqb|qb|

ca＝gf/c

cf＝fδt/2df

式中，d为当量直径，f为管路断面等效面积，f为综合水头损失系数，c为压力波速，cp、cn、ca、cf为特征线水击特征参数，qa、qb、qp为对应节点a、b、p处流量，ha、hb、hp为对应节点a、b、p处水头。

2)基于改进suter变换的水泵水轮机插值模型，能够消除全特性曲线在“s”特性区交叉、多值的影响，基于改进suter变换的水泵水轮机插值模型公式如下：

式中，x、q、h、mt、y分别为机组转速、流量、水头、转矩和开度相对值，xqa为相对流量角，k1、k2、cy、ch均为常数，k1＞|m11max|/m11r，m11r为额定单位转矩，m11max为单位转矩最大值，k2＝0.5～1.2，cy＝0.1～0.3，ch＝0.4～0.6。

3)两级电液随动装置为主配压阀-主接力器两级结构，考虑随动装置死区、主接力器限速与主接力器限幅等非线性环节。所述两级电液随动装置的主配压阀和主接力器计算公式分别如下：

其中，u为两级电液随动装置输入，yb为主配压阀输出，y为主接力器输出，k0为主配压阀放大系数，tyb为主配压阀时间常数，ty为主接力器时间常数，s为拉普拉斯算子。

4)发电机及负载模型表达式如下：

其中，x为机组转速响应相对值，mt为机组转矩相对值，ta为机组惯性时间常数，en为发电机组自调节系数，s为拉普拉斯算子。

进一步，所述步骤4中，以多目标人工羊群算法(关于人工羊群算法在中国专利申请号cn201510759863.1已经公开)为例，包括以下子步骤：

1)初始化非线性抽水蓄能机组调速系统精细化模型参数、人工羊群算法参数及群体中个体的位置；

2)依据建立的hgs-npid控制参数优化的多目标函数，计算羊群中所有个体的目标函数值，采用赌轮选择法选择一个个体作为当前最优个体；

3)按照多目标人工羊群算法随机搜索、头羊效应、淘汰优选和反演重构四种搜索机制，更新个体位置，获得种群当前最优参数解；

4)重复步骤2)和步骤3)，直至达到最大迭代次数或预设精度，则停止参数优化搜索，得到的最优参数解即为hgs-npid控制器的最优控制参数。

本发明方法中，首先构建了hgs-npid控制器，其次建立非线性抽水蓄能机组调速系统精细化模型，接着建立非线性抽水蓄能机组调速系统hgs-npid控制参数优化的多目标函数，最后采用多目标智能优化算法对多目标函数进行优化，得到适用于非线性抽水蓄能机组调速系统的hgs-npid最优控制参数。

更具体的，与现有技术相比，本发明有如下优点和效果：

(1)本发明公开的非线性抽水蓄能机组调速系统启发式增益自适应pid控制方法中，hgs-npid控制器在设计上保留传统pid控制器结构，遵循“简单性优先”原则，编程简单、可移植性强，相比神经网络pid、滑模变结构控制等其他非线性控制器，更能满足实际电站调速器高速采样性能需求，具有较好的工程应用价值。

(2)本发明公开的非线性抽水蓄能机组调速系统启发式增益自适应pid控制方法中，增益自适应函数能根据工况点变化在线自动调整控制增益，能适应不同水头工况下的调节特性，能提升机组低水头空载工况下的动态品质。

(3)本发明公开的非线性抽水蓄能机组调速系统启发式增益自适应pid控制方法中，增益自适应函数构造受电容间场强平衡作用原理启发，具有直观物理意义，与现有的凭借经验公式构造的非线性pid控制方法相比，非线性构造效率较高，并且可调参数适当减少，有利于参数优化和工程调试。

附图说明

图1为本发明方法的流程示意图；

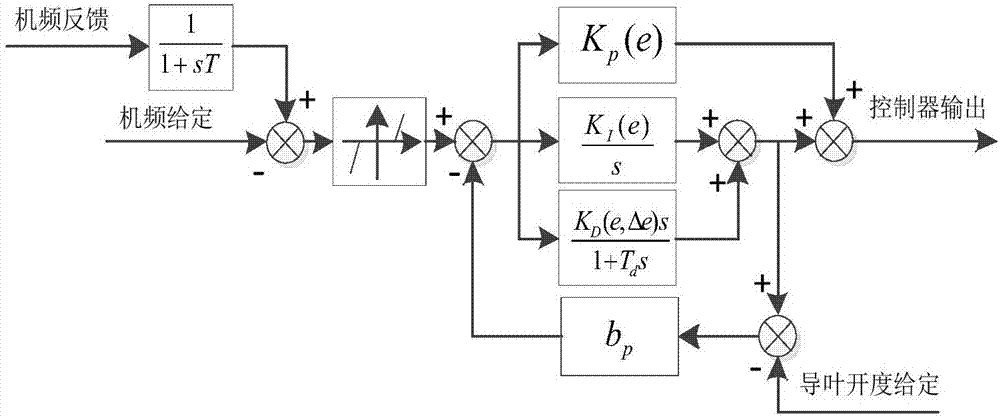
图2为本发明hgs-npid控制器模型图；

图3为本发明抽水蓄能机组调速系统精细化模型耦合框图；

图4为本发明抽水蓄能机组调速系统各模块迭代仿真流程图；

图5为有压过水系统管路布置示意图；

图6为两级电液随动装置结构图；

图7为540m水头空载开机转速响应对比图；

图8(a)为527m水头空载开机转速响应对比图；

图8(b)为527m水头空载开机转速响应局部放大图；

图9为527m水头空载开机转矩响应对比图；

图10为535m水头空载频率扰动转速响应对比图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实例仅用以解释本发明，并不用于限定本发明。此外，下面所描述的本发明各个实施方式中所涉及到的技术特征只要彼此之间未构成冲突就可以相互组合。

图1为本发明方法的流程示意图，由图可知，本发明方法中，本发明公开的一种针对非线性抽水蓄能机组调速系统的启发式增益自适应pid控制方法，首先以简单实用的并联pid控制结构为基础，受电容间场强平衡作用原理启发并引入专家控制经验，建立启发式增益自适应pid(heuristicgain-schedulingnonlinearpid，hgs-npid)控制器；同时构建非线性抽水蓄能机组调速系统精细化模型，包括调速器模型、基于特征线法的有压过水系统模型、基于改进suter变换的水泵水轮机插值模型、发电机及负载模型；接着建立非线性抽水蓄能机组调速系统hgs-npid控制参数优化的多目标函数；进一步，运用多目标人工羊群(multi-objectiveartificialsheepalgorithm，moasa)算法对非线性抽水蓄能机组调速系统hgs-npid控制参数进行优化。

为说明本发明效果，下面以某一抽水蓄能机组调速系统作为本发明的实施对象对本发明方法进行详细说明：

步骤1：构建hgs-npid控制器模型如图2所示，其比例、积分、微分环节的增益自适应函数表达式分别如下：

kd(e,δe)＝kda*exp(e*sign(δe))+kdb

以位置型并联pid结构为基础，hgs-npid控制器表达式如下：

为满足微机调速器采样需求，上述连续性方程upid需写成离散形式，表达式如下：

ek＝xk-xo

δek＝(ek-ek-1)/ts

ud,k＝kd(ek,δek)/(td+ts)*δek+td/(td+ts)*ud,k-1

其中，upid,k为控制器输出、k为仿真步数、xo为机组转速给定、xk为第k次仿真机组转速响应、ek-1为第k-1次仿真的控制误差、ek为第k次仿真的控制误差、δek为第k次仿真的控制误差变化率、ud,k-1为第k-1次仿真积分环节控制输出、ud,k为第k次仿真积分环节控制输出、采样时间间隔ts为0.02s、积分时间常数td为1，j为0、1···、k。hgs-npid控制器中误差最大值e0、比例增益调节系数m、比例增益幅值kpmax、积分增益调节系数b、积分增益幅值kimax、微分增益调节系数kda和kdb为需要优化的控制参数。

步骤2：建立非线性抽水蓄能机组调速系统精细化模型，其结构耦合框图如图3，已知n时刻的机组工况参数，过水系统各部分的流量和水压以及n+1时刻调速器输出导叶开度yn+1，并将其初始化成n+1时刻系统各模块参数。

具体的，首先由水泵水轮机插值模型得n+1时刻水头hn+1和力矩mn+1，然后，将hn+1输入到过水系统模型中求解n+1时刻流量qn+1，接着由发电机及负载方程根据n时刻及n+1时刻主动力矩和负载力矩由发电机及负载方程求解n+1时刻机组转速an+1，由于抽水蓄能机组调速系统各模块间的非线性耦合关系，需对当前时刻机组相对流量和相对转速分别进行迭代计算，才能计算下一时刻抽水蓄能机组调速系统各模块的响应结果，其仿真迭代流程图如图4。

建模过程包括如下子步骤：

1)利用调整波速法对有压过水系统进行管路划分，管路布置为单管单机方式，如图5所示，其有压过水系统具体参数如表1。

表1有压过水系统参数表

对表1中的每段管道及边界列写正负波速±c下特征线方程，其表达式如下：

其中：

cp＝qa+caha-cfqa|qa|

cn＝qb-cahb-cfqb|qb|

ca＝gf/c

cf＝fδt/2df

式中，d为当量直径，f为管路断面等效面积，f为综合水头损失系数，c为压力波速，cp、cn、ca、cf为特征线水击特征参数，qa、qb、qp为对应节点a、b、p处流量，ha、hb、hp为对应节点a、b、p处水头。

2)采用改进suter变换方法对水泵水轮机全特性曲线进行处理，表达式如下。

式中，x、q、h、mt、y分别为机组转速、流量、水头、转矩和开度相对值，xqa为相对流量角，k1、k2、cy、ch均为常数，k1＝10，k2＝0.9，cy＝0.2，ch＝0.5。

3)构建两级电液随动装置如图6所示，主配压阀和主接力器表达式依次如下：

其中，u两级电液随动装置输入，yb为主配压阀输出，y为主接力器输出，s为拉普拉斯算子，主配压阀放大系数k0＝7，主配压阀时间常数tyb＝0.05，主接力器时间常数ty＝0.2。

在图6中，两级电液随动装置死区设置为0.0137，主接力器限幅环节最小行程相对值为0，最大行程相对值为1.12，主接力器限速环节上下限相对值分别为llim_open＝0.01244、llim_close＝-0.00747。

4)发电机及负载模型表达式如下：

其中，x为机组转速响应相对值，mt为机组转矩相对值，机组惯性时间常数ta为8.503，发电机组自调节系数en为0.1，s为拉普拉斯算子。

步骤3：建立上述抽水蓄能机组调速系统的hgs-npid控制参数优化的多目标函数，采用时间误差平方积分itse指标和误差平方积分ise指标作为hgs-npid控制参数优化目标函数，分别定义为：

itse指标：

ise指标：

式中，c(k)为频率给定值序列，x(k)为机组转速响应序列，ns为采样点数，t(k)为时间序列。优化向量θ为[e0、m、kpmax、b、kimax、kda、kdb]，其中，e0为误差最大值、m为比例增益调节系数、kpmax为比例增益幅值、b为积分增益调节系数、kimax为积分增益幅值、kda和kdb为微分增益调节系数。

步骤4：运用多目标人工羊群算法求解步骤3中的hgs-npid控制参数优化的多目标函数，具体包含如下子步骤：

step1：设置算法参数，总迭代数q＝100，群体规模n＝20，档案集规模nrep＝30，个体随机搜索数nl＝3，淘汰幅度系数σ＝0.01，跳跃阈值p＝100；误差最大值e0、比例增益调节系数m、比例增益幅值kpmax、积分增益调节系数b、积分增益幅值kimax、微分增益调节系数kda和kdb的优化范围构成控制参数变量θ的优化区间为[bl；bu]，其中θ的优化下限bl＝[0.1,1,0.1,-5,0.1,0.1,0.1]，优化上限bu＝[3,20,10,3,3,3,8]。在优化区间[bl；bu]中初始化群体中所有个体的位置向量，个体位置向量xi,i＝1,...,n代表一组控制参数，令当前迭代次数t＝0；

step2：计算个体的目标函数值fi^t＝[fitse(xi(t)),fise(xi(t))],i＝1,...,n，具体过程如下：从个体i位置向量xi(t)解码得到hgs-npid控制参数e0、m、kpmax、b、kimax、kda、kdb，将控制参数输入到步骤2的非线性抽水蓄能机组调速系统精细化模型中，仿真得到抽水蓄能机组各状态变量随时间的变化过程，采集机组转速响应相对值x，采样时间间隔设置为0.02s，得到机组转速响应序列x(k)，并记录时间序列t(k)。

按照步骤(3)中hgs-npid控制参数优化的多目标函数公式计算个体i的目标函数值fi^t。重复上述过程直至计算出整个种群所有个体的目标函数值。

进一步，以hgs-npid控制参数优化的多目标函数为基础，对群体中的所有个体进行非支配排序，并给每个个体设定支配性标记，将标记为“未被支配”的个体加入档案集；

step3:运用网格法确定档案集中最不拥挤，即个体数量最少的网格，并采用赌轮选择法在该网格中选择一个个体作为头羊向量xb(t)。

step4:对所有个体xi,i＝1,...,n进行随机搜索，观望一个位置

以该位置草质是否更优为条件，形成惯性向量

式中，rand为(0,1)之间随机数，个体搜索因子εstep＝0.2·||bu-bl||、εplay＝0.1·||bu-bl||。个体需进行nl次随机搜索。

step5:计算每个个体xi(t)受当前头羊影响的召唤向量

其中，δi为第i个个体与当前最优个体的距离向量，头羊召唤因子c1＝2·rand、c2＝(2·rand-1)(1-t/q)，其中t为迭代步数，q为迭代总数。

step6:按照个体位置更新公式更新个体位置xi(t+1)：

若更新后个体位置超出位置边界[bl；bu]，则令超出的位置分量等于相应的边界值。

step7:更新档案集：

step7.1：计算位置更新后的群体hgs-npid控制参数优化的多目标函数，并确定多目标函数更新后的群体支配关系。将未被支配的个体加入档案集。

step7.2：确定档案集中个体之间的支配关系，将被支配的个体从档案集中删除。

step7.3：若档案集中个体数量仍超过档案集规模nrep，运用网格法找出档案集中最拥挤的网格，即个体数量最多的网格，并利用赌轮选择法随机选择该网格中一个个体从档案集中删除。重复此法直至档案集中个体数量不大于nrep。

step8:判断是否连续p代当前最优个体位置未发生移动，如果是，则认为种群灭亡，按照下式反演重构新的种群：

其中，r为反演半径r＝0.1·||bu-bl||；rand为(0，1)之间随机数，p为跳跃阈值；

step9:t＝t+1，如果t>q，算法结束，输出当前最优个体位置作为终解；否则，转入step3。当前最优个体位置即为最优控制参数向量。

为比较本发明所述方法的性能，引入传统pid和分数阶pid(又称为：fopid)控制器作对比。对540m额定水头空载工况下各控制器的控制参数进行优化，优化结果如表2。其中，kp、ki、kd分别为传统pid控制器和分数阶pid控制器的比例增益、积分增益、微分增益，λ为分数阶pid控制器的积分算子系数，μ为分数阶pid控制器的微分算子系数，误差最大值e0、比例增益调节系数m、比例增益幅值kpmax、积分增益调节系数b、积分增益幅值kimax、微分增益调节系数kda和kdb为hgs-npid控制器的控制参数。设置不同水头条件下空载开机和空载频率扰动试验。

表2控制参数优化表

(1)空载开机

空载开机试验包括540m和527m两种水头工况，各控制器参数按表2设置。空载开机时不同控制器在不同水头下的控制效果如图7、8所示，527m水头下空载开机转矩响应如图9所示，开机各控制器性能指标如表3所示。

表3空载开机各控制器性能指标

由图8(a)和表3可知，虽然三种控制器均使用优化后控制参数，但hgs-npid控制器仍然改善了该工况下的动态过程。当电站水头为527m时，机组运行于全特性曲线右侧“s”特性区范围增大，导致额定水头下优化的pid控制参数在低水头下振荡次数增多，具体可见图8(b)，但是hgs-npid控制下的空载开机对水头的适应性明显增强，较好的控制指标为机组低水头并网创造了良好条件。图9表明，hgs-npid控制下的机组转矩在切入自动调节后迅速稳定且振荡较少，这对延长机组寿命具有积极作用。

(2)频率扰动

在535m水头下，机组空载稳定运行至80s，施加+1hz频率扰动。由于实际运行中调速器在空载工况下仅设置一组控制参数，故本发明仍按照表2设定，以考察控制器对工况转换的适应性。空载频率扰动时不同控制器的控制效果如图10所示。空载频率扰动各控制器性能指标如表4所示。

表4频率扰动各控制器性能指标

由表4和图10可得，在低水头空载扰动工况下，pid控制的机组转速在给定值附近振荡，说明额定水头空载开机工况下优化的pid控制参数已难以适应低水头下工况点变化要求；fopid控制下动态指标虽满足国标要求，但稳态误差较大；hgs-npid控制虽然在扰动初始时刻响应速度略慢，但整体性能更好，能提高机组低水头空载工况稳定性和不同水头条件下的适应性。

本发明提出的非线性抽水蓄能机组调速系统启发式增益自适应pid控制方法实现简单、实时性强，控制增益能根据工况点变化实现在线自适应调整，既能充分适应抽水蓄能机组调速系统水击与非线性，又能改善常规控制方式在不同水头工况下的动态品质。

本领域的技术人员容易理解，以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。