一种参数自适应分数阶自抗扰自动发电控制方法与流程

本发明属于电力系统自动发电控制领域，涉及一种基于参数自适应策略、分数阶控制思想和自抗扰算法相结合的自动发电控制方法，适用于电力系统自动发电控制问题。

背景技术：

随着科技的不断发展和控制水平的不断提高，传统的比例-积分-微分控制器依然在自动控制技术领域广泛应用。但是实际控制系统中被控对象的参数是变化的，且随着控制器内部及外部的环境干扰变化而变化的，这样造成期望值与实际值形成一定的误差。近年来，诸多研究者针对自动发电控制、负荷频率控制和自动电压调节提出许多改进的比例-积分-微分控制器，如通过遗传算法和萤火虫算法对控制器参数进行改进的控制器。改进的控制器在一定程度上提高了控制效果。

为提高控制器的性能，研究者们提出分数阶控制思想。在过去的几十年里，分数阶系统得到较大的发展，研究者们在分数阶控制思想的基立础上建立了分数阶控制器模型，如基于分数阶比例-积分-微分控制器。当然，可通过各种优化算法来调整分数阶比例-积分微分控制器的参数，如菌群优化算法、遗传算法和蚁群优化算法等算法。但在分数阶比例-积分-微分控制器中，微分和积分的阶次不一定是整数，分数阶比例-积分-微分控制器比传统的比例-积分-微分控制器多两个可变参数，使控制器更灵活、鲁棒性更强和控制性能更高，但分数阶比例-积分-微分控制器的结构变得复杂，增加了参数调整的难度。

传统控制理论一般研究较为简单的控制系统，而现代控制理论研究更为复杂的多输入多输出的系统。现代控制理论的研究对象具有多个参数变量、变量范围广和环境复杂等特点。传统比例-积分-微分控制对实时扰动性抗干扰能力差。为此，韩京清教授提出一种新颖的控制技术，即自抗扰控制技术。自抗扰控制技术可改善传统比例-积分-微分控制器抗干扰能力差的问题。自抗扰控制器具有结构简单、抗干扰能力强、调节方便和不依赖模型等优点。自抗扰控制器可在自动发电控制系统、负荷频率控制系统和气动伺服系统中广泛应用。自抗扰控制器不依靠固定的被控模型，且可对未知的被控对象进行控制。自抗扰控制器具有较好的适应能力和自动估计补偿外部未知干扰的能力，可把复杂的控制问题变得简单化。自抗扰控制器对被控对象进行实时反馈补偿，处理内外总干扰，抑制干扰对系统产生的不良影响，增强系统的稳定性。但是，自抗扰控制器具有控制带宽高、采样间隔短和观测误差大等问题。

因此，将分数阶控制思路和自抗扰算法结合成分数阶自抗扰算法，该算法结合了两者的优点。分数阶自抗扰控制器与传统的自抗扰控制器相比，具有以下优点：

1.由于引入分数阶运算，因此分数阶自抗扰控制器比自抗扰控制器的控制性能更高。

2.根据被控对象的模型特征，可重新设计扩张状态观测器，使扩张状态更精确。

3.用分数阶控制器代替整数阶控制器，使控制器对参数可调范围更大，控制速度更为高效。

由于引入可调参数λ和μ，使得分数阶自抗扰控制器的参数整定范围变大，且需人工调整，繁琐的人工调整使得控制效果并没有那么高效。为了在无需人工调整参数的情况下得到较高的控制性能，将参数自适应策略应用于分数阶自抗扰算法中，即本发明所提供的参数自适应分数阶自抗扰控制方法。将参数自适应分数阶自抗扰控制方法应用在自动发电控制系统中，可使系统的控制性能提升。

技术实现要素：

本发明提出一种参数自适应分数阶自抗扰自动发电控制方法。该方法能够在无需人工调整参数的情况下得到较高的控制性能，且抗干扰能力强。

常规的比例-积分-微分控制器由比例部分、积分部分和微分部分组成。比例-积分-微分控制器的传递函数可表示如下：

cpid(s)＝(kp+ki/s+kds)(1)

式中，kp是比例系数，ki是积分系数，kd是微分系数。

比例-积分-微分控制器的输出可表示如下：

式中，e(t)是比例-积分-微分控制器的输入，即误差，即被控对象的输出与输入信号之间的差。

分数阶比例-积分-微分控制器与常规的比例-积分-微分控制器相比，分数阶比例-积分-微分控制器还有两个参数，即λ和μ。分数阶比例-积分-微分控制器的传递函数可表示如下：

cfopid(s)＝(kp+ki/s^λ+kds^μ)(3)

式中，λ和μ为分数阶阶次，kp、ki和kd为控制器参数。所以在分数阶比例-积分-微分控制器中，需要被调节的参数为kp、ki、kd、λ和μ。当λ＝1,μ＝1时，即为整数比例-积分-微分控制器；当kd＝0，λ＝1时，即为传统积分控制器；当ki＝0，μ＝1时，即为传统比例控制器。

分数阶比例-积分-微分控制器的输出如下：

ufopid(t)＝(kp+kid^-λ+kdd^μ)e(t)(4)

式中，d^-λ和d^μ分别是分数阶比例-积分-微分控制器的积分部分和微分部分。λ和μ分别是比例-积分-微分控制器积分部分和微分部分的阶次，且都大于0。

当λ和μ取不同值时，分数阶比例-积分-微分控制器的结构不同。分数阶比例-积分-微分控制器与整数阶比例-积分-微分控制器相比，分数阶比例-积分-微分控制器可提高控制器的灵活性。分数阶比例-积分-微分控制器具有更强的鲁棒性和更高的控制性能。但是，分数阶比例-积分-微分控制器参数整定的难度增加。

自抗扰控制技术是经典控制理论与现代控制工程结合创新而来，并逐渐优于传统控制技术。自抗扰控制技术不依靠固定的被控对象模型，且可在被控对象未知的情况下进行控制。自抗扰控制器使用范围广，具有自动估计补偿不确定外部干扰的能力，具有较强的适应性和鲁棒性。自抗扰控制器在构成上一般采用非线性函数。对于一阶控制对象，有，

式中，u为系统输入量，y为系统输出量。

一个三阶自抗扰控制器的过程可表示如下：

式中，b0是控制对象的向量增益，y是输出。

由于自抗扰控制器具有强鲁棒性、抗干扰性和无模型依赖性等优点，可将自抗扰控制器应用在分数阶系统，即将分数阶控制思想和自抗扰算法结合成分数阶自抗扰算法。分数阶自抗扰算法可使控制器的阶次选择范围更广、性能更高和抗干扰能力更强。分数阶自抗扰控制器由分数阶跟踪微分器、分数阶扩张状态观测器和分数阶状态误差反馈组成。在分数阶控制器中加入扩张状态观测器，使分数阶自抗扰控制器比传统的比例-积分-微分控制器具有更好的控制效果、更好的稳定性和更强的抗干扰能力。扩张状态观测器可表示如下：

式中，是x的估计状态向量，是系统y的估计输出，l＝(l1l2l3l4)^t是扩张状态观测器的增益向量。扩张状态观测器具有较多参数，每个参数都会影响系统的性能，所以应对参数进行调整。扩张状态观测器的稳定是自抗扰控制器稳定的必要条件。

由于分数阶自抗扰控制器加入了分数阶控制思想，所以分数阶自抗扰控制器比传统自抗扰控制器多了两个可变参数，可提高控制器的灵活性和控制性能。但分数阶自抗扰控制器结构更为复杂，增加了参数调整难度。为了在无需人工调整参数的情况下得到较高的控制性能，将参数自适应策略应用于分数阶自抗扰算法中，参数自适应算法对系统的参数进行自动调整，免去人工调整的麻烦。

在针对电力系统自动发电控制问题时，参数自适应分数阶自抗扰自动发电控制方法以系统的频率偏差和区域控制误差为输入，以功率缺额为输出。

附图说明

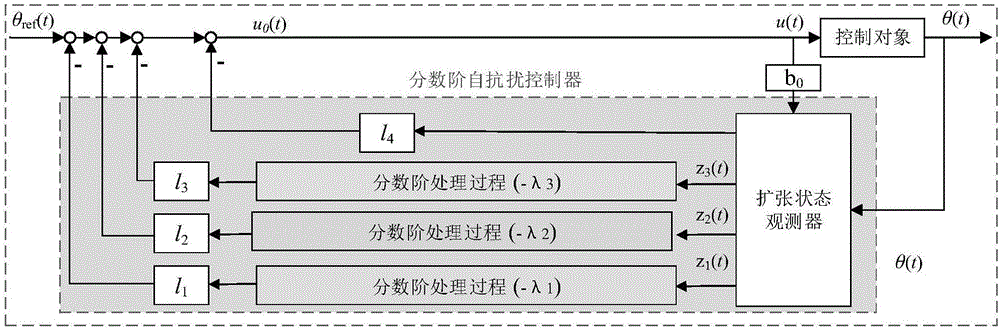
图1是参数自适应分数阶自抗扰控制器结构图。

图2是比例-积分-微分控制器、分数阶比例-积分-微分控制器、自抗扰控制器和分数阶自抗扰控制器的控制空间图。

具体实施方式

本发明提出的一种参数自适应分数阶自抗扰自动发电控制方法，结合附图详细说明如下：

图1是本发明方法的参数自适应分数阶自抗扰控制器结构图。分数阶自抗扰控制器由分数阶扩张状态观测器和分数阶状态误差反馈组成。分数阶自抗扰控制器结合分数阶控制思想和自抗扰算法的优点，可获得更高的性能以及更强的抗干扰能力。分数阶控制器的设计是对自抗扰控制器鲁棒性能的提升。以三阶结构的分数阶自抗扰控制器为例，三阶结构的分数阶自抗扰控制器具有三个参数，即λ1，λ2和λ3。分数阶自抗扰控制器的输出表示如下：

分数阶自抗扰控制器的核心是分数阶扩张状态观测器。分数阶扩张状态观测器将系统内部和外部干扰都看为未知干扰，分数阶扩张状态观测器实现对被控对象扰动误差的估计补偿，同时增强了分数阶自抗扰控制器的抗干扰能力。将参数自适应策略应用于分数阶自抗扰算法中，可使系统在无需人工调整参数的情况下得到较高的控制性能

图2是比例-积分-微分控制器、分数阶比例-积分-微分控制器、自抗扰控制器和分数阶自抗扰控制器的控制空间图。由于在自抗扰控制器中加入分数阶控制思想，使得分数阶自抗扰控制器的阶次可调范围更广。当分数阶自抗扰控制器的参数等于1时，即λ1＝λ2＝λ3＝1，即为普通的自抗扰控制器，自抗扰控制器的性能并没有提高。因此，为了获得更高的控制性能，分数阶自抗扰控制器的分数阶参数可设置λ1、λ2和λ3都大于0。当λ＝0，μ＝0时，为比例控制器；当λ＝0,μ＝1时，为传统微分控制器；当λ＝1,μ＝0为传统积分控制器；当λ＝1,μ＝1时为传统比例-积分-微分控制器。传统的比例-积分-微分控制器只能取图中的四个点，分数阶比例-积分-微分控制器可取图中任意的点。自抗扰算法具有良好的鲁棒性以及抗干扰性，将分数阶控制思想和自抗扰算法结合成分数阶自抗扰算法，该算法结合了两者的优点，使得分数阶自抗扰控制器的控制对象范围更广大，能提高系统的控制性能，且增强抗干扰能力。常规比例-积分-微分控制器的抗干扰能力最弱，分数阶比例-积分-微分控制器则次之，自抗扰控制器具有较强的抗干扰能力。分数阶自抗扰控制器由于加入了自抗扰控制器的扩张状态观测器，能较好的估计补偿扰动，所以具有较强的抗干扰能力。分数阶自抗扰控制器在抗干扰能力和鲁棒性上，优于分数阶控制器，具有更好的控制性能。