一种改进的全局滑模控制方法与流程

本发明属于自动控制技术领域，具体涉及一种改进的全局滑模控制方法。

背景技术：

滑模控制对于建模不确定和外部干扰信号具有很强的鲁棒性，并具有响应速度快和容易实现等优点，经常用于非线性系统的控制。采用线性滑模面的普通滑模控制分为趋近模态和滑动模态，且只在滑动模态具有鲁棒性，在趋近模态没有鲁棒性。全局滑模控制是通过设计动态非线性滑模面来实现的，在趋近模态和滑动模态的全过程都具有鲁棒性。全局滑模控制器具有比普通滑模控制器更好的鲁棒性，具有非常广泛的应用。

传统的全局滑模控制方法中，全局滑模面中函数p(t)采用单调的指数衰减形式，即p(t)＝p(0)e^-βt，其中β>0，当t→∞时，p(t)→0，函数p(t)不能在有限的时间内收敛到零，因此状态变量收敛的速度较慢。因此，设计改进的全局滑模面和改进的全局滑模控制器非常的必要。

技术实现要素：

基于以上的技术问题，本发明提供一种改进的全局滑模控制方法，对于带有建模不确定和外部干扰信号的三阶严反馈系统，设计改进的全局滑模面，全局滑模面中函数p(t)能够在设定的有限时间内收敛到零，采用改进的全局滑模面和指数趋近律设计全局滑模控制器，该全局滑模控制器对三阶严反馈系统进行平衡控制，形成闭环系统，该闭环系统能够实现三阶严反馈系统的平衡控制，状态变量收敛的速度非常快，对建模不确定和外部干扰信号具有较好的鲁棒性。

所述一种改进的全局滑模控制方法，包括以下步骤：

步骤1：建立带有建模不确定和外部干扰信号的三阶严反馈系统；

其中，x1，x2和x3为系统的状态变量，x＝[x1,x2,x3]^t，f1(x)为连续函数，△f1(x)为建模不确定，d(t)为外部干扰信号，t为时间，u为控制输入，建模不确定△f1(x)和外部干扰信号d(t)均有界，即|△f1(x)|≤d1，|d(t)|≤d2，且d1≥0，d2≥0。

步骤2，设计改进的全局滑模面s：

s＝x3+2λx2+λ²x1-p(t)(2)

其中，λ为常数，且λ>0，p(t)是为了实现全局滑模控制设计的函数，p(t)能够在有限时间内收敛到零，且s(0)＝0，函数p(t)必须满足下面的三个条件：

(1)p(0)＝p0，且p0＝x3(0)+2λx2(0)+λ²x1(0)；

(2)当t→∞时，p(t)→0；

(2)p(t)具有一阶导数；

根据以上三个条件，在改进的全局滑模面公式(2)中，将函数p(t)设计为

其中，n为偶数，t0为常数，且t0>0，t为时间，当t＝0时，p(0)＝p0；当t＝t0时，p(t0)＝0，函数p(t)在t0时刻收敛到零，函数p(t)对时间t进行求导，得到

步骤3：在全局滑模控制器的设计中，采用的指数趋近律为：

其中，k1和k2为常数，且k1≥0，k2≥d1+d2；

步骤4：设计全局滑模控制器：对于三阶严反馈系统公式(1)，采用改进的全局滑模面公式(2)和指数趋近律公式(5)，全局滑模控制器设计为：

在公式(6)的控制器中存在符号函数sgn(s)，会使控制器不连续，出现抖振现象，为了削弱抖振的影响，采用连续函数con(s,δ)代替符号函数sgn(s)，最终的全局滑模控制器设计为：

其中，连续函数con(s,δ)的表达式为δ为常数，且δ>0。

步骤5：用全局滑模控制器对三阶严反馈系统进行平衡控制，形成闭环系统，该闭环系统能够实现三阶严反馈系统的平衡控制，即对建模不确定和外部干扰信号具有鲁棒性。

通过lyapunov稳定性理论对闭环系统的稳定性进行证明，lyapunov函数为：

其中，s是公式(2)中定义的改进的全局滑模面，对公式(8)进行求导，并将公式(1)和公式(2)带入公式(8)求导后公式，得到：

将公式(6)带入到公式(9)并化简后可以得到：

由于v≥0，由lyapunov稳定性理论证明了由公式(1)和公式(6)组成的闭环系统是稳定的，三阶严反馈系统的状态变量渐进收敛到零，即能够实现三阶严反馈系统的平衡控制，对建模不确定和外部干扰信号具有很好的鲁棒性。

有益技术效果：

本发明提供的一种改进的全局滑模控制方法，设计改进的全局滑模面，全局滑模面中函数p(t)在设定的有限时间t0内收敛到零，采用改进的全局滑模面和指数趋近律设计全局滑模控制器，该全局滑模控制器能够实现三阶严反馈系统的平衡控制，具有非常快的收敛速度，对建模不确定和外部干扰信号具有很好的鲁棒性，为了削弱抖振，采用连续函数con(s,δ)代替符号函数sgn(s)。

附图说明

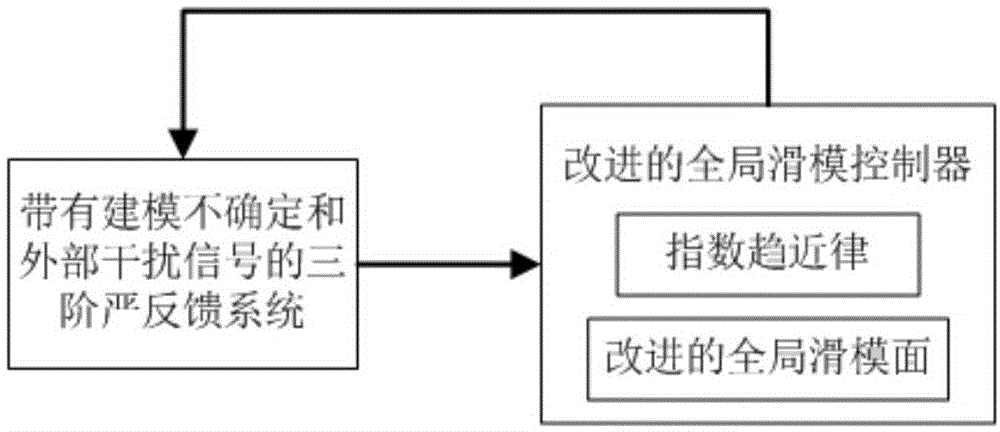
图1为本发明的总体原理图；

图2为具体实施例1中采用符号函数时控制输入的响应曲线；

图3为具体实施例1中采用连续函数时控制输入的响应曲线；

图4为具体实施例1中函数p(t)和的响应曲线；

图5为具体实施例1中状态变量的响应曲线；

图6为具体实施例2中采用符号函数时控制输入的响应曲线；

图7为具体实施例2中采用连续函数时控制输入的响应曲线；

图8为具体实施例2中函数p(t)和的响应曲线；

图9为具体实施例2中状态变量的响应曲线；

图10为具体实施例1和2的流程图；

具体实施方式

下面结合附图和具体实施实例对发明做进一步说明：如图1所示，根据带有建模不确定和外部干扰信号的三阶严反馈系统，设计改进的全局滑模面，采用改进的全局滑模面和指数趋近律设计全局滑模控制器，该全局滑模控制器和三阶严反馈系统形成闭环控制系统，该闭环控制系统实现三阶严反馈系统的平衡控制，三阶严反馈系统的状态变量渐进收敛到零，对建模不确定和外部干扰信号具有很好的鲁棒性。

为了更加直观的显示本发明提出的一种改进的全局滑模控制方法的有效性，采用matlab/simulink软件对本控制方案进行仿真实验。在仿真实验中，采用ode45算法，ode45算法即四阶-五阶runge-kutta算法，是一种自适应步长的常微分方程数值解法，最大步长为0.0001s，仿真时间为6s。

具体实施例1：

流程如图10所示：

步骤1：建立带有建模不确定和外部干扰信号的三阶严反馈系统；

其中，f1(x)＝-x1-x2-0.6x3+sgn(x1)+sgn(x1+2)+sgn(x1-2)，建模不确定△f1(x)设定为△f1(x)＝0.6sin(x2)sin(x3)，则d1＝0.6，外部干扰信号d(t)设定为d(t)＝0.6cos(2t)，则d2＝0.6，t为时间，u为控制输入。三阶严反馈系统公式(11)的初始状态设定为x1(0)＝2，x2(0)＝-1，x3(0)＝-2。

步骤2，设计改进的全局滑模面s：

s＝x3+2λx2+λ²x1-p(t)(2)

其中，参数设定为λ＝4。

在改进的全局滑模面中，函数p(t)为公式(3)：

其中，参数设定为t0＝1，n＝4，p0＝x3(0)+2λx2(0)+λ²x1(0)＝22。

步骤3：在全局滑模控制器的设计中，采用的指数趋近律为公式(5)：

其中，参数设定为λ1＝2，λ2＝d1+d2＝1.2。

步骤4：设计全局滑模控制器：对于三阶严反馈系统公式(1)，采用改进的全局滑模面公式(2)和指数趋近律公式(5)，设计的全局滑模控制器为公式(6)：

为了削弱抖振的影响，采用连续函数con(s,δ)代替符号函数sgn(s)，最终设计的全局滑模控制器为公式(7)：

其中，连续函数con(s,δ)的表达式为参数设定为δ＝0.001。

步骤5：用全局滑模控制器对三阶严反馈系统进行平衡控制，形成闭环系统，该闭环系统能够实现三阶严反馈系统的平衡控制，即对建模不确定和外部干扰信号具有鲁棒性。

控制参数如前所设，进行系统的仿真。图2是采用符号函数sgn(s)时，全局滑模控制器的控制输入曲线。图3是采用连续函数con(s,δ)代替符号函数sgn(s)后，全局滑模控制器的控制输入曲线。在图2中，控制输入出现了明显的抖振现象，在图3中，控制输入比较平滑，没有出现抖振现象。图4是函数p(t)和的响应曲线，函数p(t)和在t0＝1s时收敛到零。图5是状态变量的响应曲线，状态变量渐进收敛并在2.8s时基本收敛到零，状态变量收敛的速度非常快。从仿真曲线可以直观的观察到，采用改进的全局滑模控制器能够实现三阶严反馈系统的平衡控制，状态变量快速收敛到零，能够克服建模不确定和外部干扰信号的影响，具有很好的鲁棒性和可靠性。

具体实施例2：

流程如图10所示：

步骤1：建立带有建模不确定和外部干扰信号的三阶严反馈系统；

其中，f1(x)＝-x1-1.1x2-0.45x3+x1²，建模不确定△f1(x)设定为△f1(x)＝cos(x1)sin(x2)，则d1＝1，外部干扰信号d(t)设定为d(t)＝sin(3t)，则d2＝1，t为时间，u为控制输入。三阶严反馈系统公式(12)的初始状态设定为x1(0)＝3，x2(0)＝-2，x3(0)＝-3。

步骤2，设计改进的全局滑模面，改进的全局滑模面为公式(2)：

s＝x3+2λx2+λ²x1-p(t)(2)

其中，参数设定为λ＝4.5。

在改进的全局滑模面中，函数p(t)为公式(3)：

其中，参数设定为t0＝1.2，n＝4，p0＝x3(0)+2λx2(0)+λ²x1(0)＝39.75。

步骤3：在全局滑模控制器的设计中，采用的指数趋近律为公式(5)：

其中，参数设定为λ1＝2，λ2＝d1+d2＝2。

步骤4：设计全局滑模控制器：对于三阶严反馈系统公式(1)，采用改进的全局滑模面公式(2)和指数趋近律公式(5)，设计的全局滑模控制器为公式(6)：

为了削弱抖振的影响，采用连续函数con(s,δ)代替符号函数sgn(s)，最终设计的全局滑模控制器为公式(7)：

其中，连续函数con(s,δ)的表达式为参数设定为δ＝0.001。

步骤5：用全局滑模控制器对三阶严反馈系统进行平衡控制，形成闭环系统，该闭环系统能够实现三阶严反馈系统的平衡控制，即对建模不确定和外部干扰信号具有鲁棒性。

控制参数如前所设，进行系统的仿真。图6是采用符号函数sgn(s)时，全局滑模控制器的控制输入曲线。图7是采用连续函数con(s,δ)代替符号函数sgn(s)后，全局滑模控制器的控制输入曲线。在图6中，控制输入出现了明显的抖振现象，在图7中，控制输入比较平滑，没有出现抖振现象。图8是函数p(t)和的响应曲线，函数p(t)和在t0＝1.2s时收敛到零。图9是状态变量的响应曲线，状态变量渐进收敛并在2.8s时基本收敛到零，状态变量收敛的速度非常快。从仿真曲线可以直观的观察到，采用改进的全局滑模控制器能够实现三阶严反馈系统的平衡控制，状态变量快速收敛到零，能够克服建模不确定和外部干扰信号的影响，具有很好的鲁棒性和可靠性。