基于事件触发的四旋翼无人机一致性编队控制方法与流程

本发明属于自动驾驶及控制技术领域，具体涉及基于事件触发的四旋翼无人机一致性编队控制方法。

背景技术：

四旋翼无人机具有尺寸小、速度快、可垂直升降、机动性强等优势，在军事、农业、消防电力等领域都有很好的应用。多无人机组成编队协同作业，可弥补单个无人机荷载有限的缺陷，极大提高四旋翼无人机的任务能力。

但传统一致性编队控制算法随着无人机编队规模增大，无人机间通讯量呈指数上升，亟需一种新的控制算法，节约通讯资源且能实现四旋翼无人机的一致性编队控制。

相比于传统周期采样控制，基于事件触发的控制更加的灵活且智能，控制信息的传输和更新仅在定义的“事件”被触发之后。

事件触发算法极大的节约了网络的带宽和通讯资源，非常适合用于大规模一致性编队控制。

因此，本发明公开了一种基于事件触发的四旋翼无人机一致性编队控制方法，弥补此方面的空缺。

技术实现要素：

发明目的：本发明的目的在于提供基于事件触发的四旋翼无人机一致性编队控制方法，针对编队控制时无人机间通讯量巨大的问题，设计事件触发控制器控制四旋翼无人机群。

技术方案：为实现上述目的，本发明提供如下技术方案：

基于事件触发的四旋翼无人机一致性编队控制方法，包括以下步骤：

步骤1)假设编队中有n架参数相同的四旋翼无人机，n为大于1的正整数，对无人机进行受力分析，利用欧拉方程为每个四旋翼无人机建立位置子系统和姿态子系统的数学模型；

步骤2)针对位置子系统，为每个无人机设计基于事件触发的虚拟控制器，并定义事件函数计算虚拟控制器值的更新时间；

步骤3)将位置子系统的虚拟控制器视为实际控制器的输入目标，反解出每个无人机的设定姿态，并设计限定时间的姿态控制器，控制姿态角达到设定值。

进一步的，步骤1)中，所述的数学模型中，无人机i的位置子系统模型如下：

上式中代数角标i＝1,2,···,n；i表示四旋翼无人机的编号；t是时间变量，单位为秒；三维空间中用xi(t),yi(t),zi(t)描述无人机i的位置信息，单位为米；xi”(t),yi”(t),zi”(t)是位置对时间的二阶导数，物理含义是加速度，单位为米每秒的平方；θi,ψi是θi(t),ψi(t)的简写，分别表示无人机的俯仰、翻滚、偏航三个姿态角，单位为弧度；m表示无人机的质量，单位为千克；g为重力加速度，单位为米每秒的平方；f1i为无人机i的第一个控制输入，单位为牛顿。

进一步的，步骤1)中，所述的数学模型中，每个无人机的位置子系统模型如下：

上式中j^x,j^y,j^z分别表示无人机绕x,y,z轴的转动惯量，单位为千克米的平方；无人机i俯仰、翻滚、偏航姿态的角速度和角加速度分别用θi',θi”,ψi',ψi”表示，加速度、角加速度单位分别为弧度每秒、弧度每秒的平方；f2i,f3i,f4i为无人机i的第二个控制输入、第三个控制输入和第四个控制输入，单位为牛顿。

进一步的，步骤2)中，针对位置子系统，为每个无人机设计基于事件触发的虚拟控制器，具体过程如下：

对于无人机i，将位置子系统输入视为虚拟输入，得到位置子系统模型为：

为无人机i在x,y,z方向的虚拟控制输入；设计无人机i的虚拟控制输入成如下形式：

公式(4)中j是无人机编号角标，取值范围与i相同；为控制器参数；aij表示无人机i与j之间的通讯连接关系，若存在通讯连接aij＝1，否则aij＝0；tk是虚拟控制器值第k次更新的时间点，k为大于等于零的整数，t0＝0。

进一步的，步骤2)中，所述的定义事件函数计算虚拟控制器值的更新时间，具体计算过程如下：

首先定义向量x(t)＝[x1(t),x2(t),···,xn(t)]^t，则x(tk)＝[x1(tk),x2(tk),···,xn(tk)]^t；定义中间状态向量和其中矩阵l＝d-a是矩阵a的laplace矩阵；a是n维矩阵，第i行j列元素为aij；d是n维对角矩阵，第i行i列元素为非对角线上的元素皆为0；其次，定义x轴方向的事件函数f^x(t)：

其中ε^x,为事件函数的参数。参照w^x,e^x,f^x(t)形式，定义w^y,e^y,f^y(t)和w^z,e^z,f^z(t)；

最后，计算控制器值的更新时间tk+1，计算公式如下：

进一步的，步骤3)中，所述的将位置子系统的虚拟控制器视为实际控制器的输入目标，反解出每个无人机的设定姿态，其具体过程如下：

根据公式(4)和公式(1)，对于无人机i＝1,2,···,n，实际控制器的目标如下(左边θi,ψi,f1i为输入，右边为控制目标)：

根据公式(7)中控制目标反解出的输入为设定输入，用表示；三个方程四个变量，选择作为游离变量，并取得到其余设定值表达式如下：

进一步的，步骤3)中，所述的设计限定时间的姿态控制器，其具体过程如下：定义中间状态变量将中间变量带入公式(2)，并定义虚拟控制输入对无人机i的状态变量θi,ψi设计控制器如下：

上式中δ泛指状态变量θ,ψ，其中函数<*>^h的定义为<x>^h＝|x|^h·sign(x)；sign(x)为标准符号函数，若x＞0则sign(x)＝1，若x＜0则sign(x)＝-1，若x＝0则sign(x)＝0；γ^δ为控制器参数，可以调节收敛速度；函数最后取根据和f1i反向运算，即可得到无人机i的无人机i的第二个控制输入、第三个控制输入和第四个控制输入分别为f2i,f3i,f4i；在此控制输入下，无人机i的姿态在限定时间内会跟随上姿态的设定值，同时实现基于事件触发的四旋翼无人机一致性编队控制。

有益效果：与现有技术相比，本发明的基于事件触发的四旋翼无人机一致性编队控制方法，通过假设编队中有n架参数相同的四旋翼无人机(n为大于1的正整数)，对无人机进行受力分析，利用欧拉方程为每个四旋翼无人机建立位置子系统和姿态子系统的数学模型；然后，针对位置子系统，为每个无人机设计基于事件触发的虚拟控制器，并定义事件函数计算虚拟控制器值的更新时间；最后，将位置子系统的虚拟控制器视为实际控制器的输入目标，反解出每个无人机的设定姿态，并设计限定时间的姿态控制器，控制姿态角达到设定值。本发明实现了对四旋翼无人机编队的有效控制，并节约了无人机之间通讯量。

附图说明

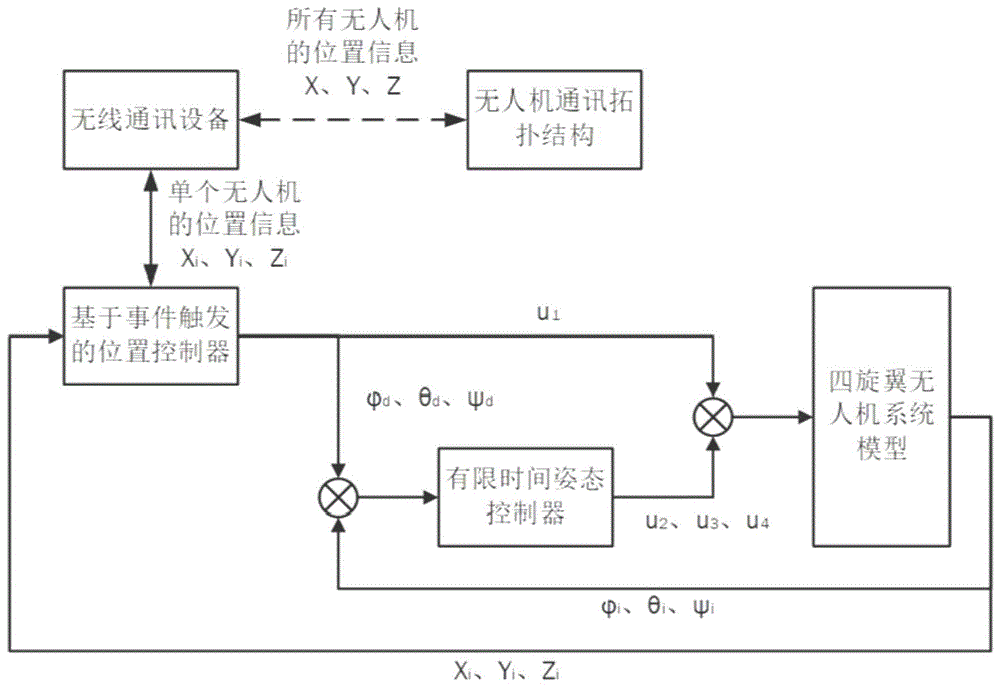
图1为单个无人机事件触发控制结构图；

图2为四旋翼无人机状态量与坐标系的对应关系；

图3为四旋翼无人机之间的拓扑通讯结构图；

图4为基于事件触发的四旋翼无人机一致性编队控制效果图。

具体实施方式

为了更好地理解本发明专利的内容，下面结合附图和具体实施例来进一步说明本发明的技术方案。

基于事件触发的四旋翼无人机一致性编队控制方法，包括以下步骤：

步骤1)假设编队中有n架参数相同的四旋翼无人机，n为大于1的正整数，对无人机进行受力分析，利用欧拉方程为每个四旋翼无人机建立位置子系统和姿态子系统的数学模型；

步骤2)针对位置子系统，为每个无人机设计基于事件触发的虚拟控制器，并定义事件函数计算虚拟控制器值的更新时间；

步骤3)将位置子系统的虚拟控制器视为实际控制器的输入目标，反解出每个无人机的设定姿态，并设计限定时间的姿态控制器，控制姿态角达到设定值。

步骤1)中，数学模型中，无人机i的位置子系统模型如下：

上式中代数角标i＝1,2,···,n；i表示四旋翼无人机的编号；t是时间变量，单位为秒；三维空间中用xi(t),yi(t),zi(t)描述无人机i的位置信息，单位为米；xi”(t),yi”(t),zi”(t)是位置对时间的二阶导数，物理含义是加速度，单位为米每秒的平方；θi,ψi是θi(t),ψi(t)的简写，分别表示无人机的俯仰、翻滚、偏航三个姿态角，单位为弧度；m表示无人机的质量，单位为千克；g为重力加速度，单位为米每秒的平方；f1i为无人机i的第一个控制输入，单位为牛顿。

步骤1)中，数学模型中，每个无人机的位置子系统模型如下：

上式中j^x,j^y,j^z分别表示无人机绕x,y,z轴的转动惯量，单位为千克米的平方；无人机i俯仰、翻滚、偏航姿态的角速度和角加速度分别用θi',θi”,ψi',ψi”表示，加速度、角加速度单位分别为弧度每秒、弧度每秒的平方；f2i,f3i,f4i为无人机i的第二个控制输入、第三个控制输入和第四个控制输入，单位为牛顿。

步骤2)中，针对位置子系统，为每个无人机设计基于事件触发的虚拟控制器，具体过程如下：

对于无人机i，将位置子系统输入视为虚拟输入，得到位置子系统模型为：

为无人机i在x,y,z方向的虚拟控制输入；设计无人机i的虚拟控制输入成如下形式：

公式(4)中j是无人机编号角标，取值范围与i相同；为控制器参数；aij表示无人机i与j之间的通讯连接关系，若存在通讯连接aij＝1，否则aij＝0；tk是虚拟控制器值第k次更新的时间点，k为大于等于零的整数，t0＝0。

步骤2)中，定义事件函数计算虚拟控制器值的更新时间，具体计算过程如下：

首先定义向量x(t)＝[x1(t),x2(t),···,xn(t)]^t，则x(tk)＝[x1(tk),x2(tk),···,xn(tk)]^t；定义中间状态向量和其中矩阵l＝d-a是矩阵a的laplace矩阵；a是n维矩阵，第i行j列元素为aij；d是n维对角矩阵，第i行i列元素为非对角线上的元素皆为0；其次，定义x轴方向的事件函数f^x(t)：

其中ε^x,为事件函数的参数。参照w^x,e^x,f^x(t)形式，定义w^y,e^y,f^y(t)和w^z,e^z,f^z(t)；

最后，计算控制器值的更新时间tk+1，计算公式如下：

步骤3)中，将位置子系统的虚拟控制器视为实际控制器的输入目标，反解出每个无人机的设定姿态，其具体过程如下：

根据公式(4)和公式(1)，对于无人机i＝1,2,···,n，实际控制器的目标如下(左边θi,ψi,f1i为输入，右边为控制目标)：

根据公式(7)中控制目标反解出的输入为设定输入，用表示；三个方程四个变量，选择作为游离变量，并取得到其余设定值表达式如下：

步骤3)中，设计限定时间的姿态控制器，其具体过程如下：定义中间状态变量将中间变量带入公式(2)，并定义虚拟控制输入对无人机i的状态变量θi,ψi设计控制器如下：

上式中δ泛指状态变量θ,ψ，其中函数<*>^h的定义为<x>^h＝|x|^h·sign(x)；sign(x)为标准符号函数，若x＞0则sign(x)＝1，若x＜0则sign(x)＝-1，若x＝0则sign(x)＝0；γ^δ为控制器参数，可以调节收敛速度；函数最后取根据和f1i反向运算，即可得到无人机i的无人机i的第二个控制输入、第三个控制输入和第四个控制输入分别为f2i,f3i,f4i；在此控制输入下，无人机i的姿态在限定时间内会跟随上姿态的设定值，同时实现基于事件触发的四旋翼无人机一致性编队控制。

实施例

如图1所示，本发明目提供一种基于事件触发的四旋翼无人机一致性编队控制方法，该方法思路是：首先，假设编队中有n架参数相同的四旋翼无人机(n为大于1的正整数)，对无人机进行受力分析，利用欧拉方程为每个四旋翼无人机建立位置子系统和姿态子系统的数学模型；然后，针对位置子系统，为每个无人机设计基于事件触发的虚拟控制器，并定义事件函数计算虚拟控制器值的更新时间；最后，将位置子系统的虚拟控制器视为实际控制器的输入目标，反解出每个无人机的设定姿态，并设计限定时间的姿态控制器，控制姿态角达到设定值。

步骤1)假设编队中有n架参数相同的四旋翼无人机(n为大于1的正整数)，对无人机进行受力分析，利用欧拉方程为每个四旋翼无人机建立位置子系统和姿态子系统的数学模型。

如图2所示四旋翼无人机，引入机体坐标系b和地面坐标系e，选取无人机i姿态角θi,ψi和无人机在三维空间中的相对位置xi,yi,zi作为数学模型的状态变量，选择无人机四个螺旋桨升力f1i,f2i,f3i,f4i作为数学模型的实际控制输入。对模型进行受力分析，建立四旋翼无人机i的数学模型如下：

步骤2)针对位置子系统，为每个无人机设计基于事件触发的虚拟控制器，并定义事件函数计算虚拟控制器值的更新时间。

一致性编队控制需要确定无人机间的拓扑通讯结构，这里选取四个无人机，即n＝4。假设图3为四旋翼无人机之间的拓扑通讯结构，计算控制器所需的laplace矩阵l。为无人机i设计公式四中的位置控制器，选取控制器参数利用公式(5)、(6)中的事件函数监测无人机位置状态，更新位置控制器的设定值。无人机位置共有x,y,z三个维度，控制器在三个维度同时运行，运行过程互不干扰，当其中任意维度的事件被触发，三个维度同时更新控制器输入值。以x维度为例，一致性编队位置控制器的运行流程如下表1：

表1.一致性编队位置控制算法输入输出表

步骤3)将位置子系统的虚拟控制器视为实际控制器的输入目标，反解出每个无人机的设定姿态，并设计限定时间的姿态控制器，控制姿态角达到设定值。

此步骤的关键是反解出每个无人机的设定姿态，根据公式(4)中设计的位置控制器和公式(1)中的位置数学模型，得到下面等式：

公式(11)中有三个等式四个未知变量θi,ψi,f1i，所以确定一个基础变量ψi＝0，得到公式(8)中无人机i的设定姿态。对每个姿态设计公式(9)中的限定时间控制器，可控制四旋翼无人机姿态达到设定值，实现一致性编队控制。

图4是四架四旋翼无人机在基于事件触发控制器下的运行轨迹图。