一种基于双层模糊强化学习的六足机器人避障方法

1.本发明属于仿生机器人领域，涉及一种基于双层模糊强化学习的六足机器人避障方法。


背景技术：

2.随着智能控制领域的快速发展和机器人的广泛应用，人们期望机器人拥有更好的自主操作能力，在更多领域代替人类完成更加复杂的操作任务。仿生机器人的研究日益发展，对于移动机器人，轮式和履带式移动机器人平台在非结构化环境下应用受到地形的限制，多足机器人因腿部具有多个自由度，使运动灵活性大大增强，地形适应能力更高。相较于二足与四足机器人，六足机器人地形环境适应能力更强，在山区建设、资源勘探、核工业、矿井巡检、星球探测等非结构环境和路况复杂领域有着非常广阔的应用前景。
3.六足机器人移动和作业过程中，需要面对动态、未知以及不易预测的非结构化的复杂环境。传统预先编程、遥操作等常规方法，需要事先针对任务分析六足机器人的移动特性，存在周期长、工作量大、效率低且不能满足任务多样性的需求等诸多难题，严重限制了六足机器人的进一步应用。因此，需要采用机器学习的方法，弥补预先编程等常规方法的缺陷，提高六足机器人对环境的适应能力。


技术实现要素：

4.本发明目的在于针对现有技术的不足，提出一种基于双层模糊强化学习的六足机器人避障方法，本发明所要解决的技术问题在于提高六足机器人对复杂环境的适应能力。
5.为达到上述目的，本发明的技术方案如下：一种基于双层模糊强化学习的六足机器人避障方法，该方法包括如下步骤：
6.s1：六足机器人前方装有三个超声波传感器，通过超声波传感器测量自身和障碍物之间的距离，并将三个超声波传感器分别测得的三个障碍物的距离进行模糊推理，将测量的连续的距离转换为离散的有限的状态，每个状态即为一个模糊规则；
7.s2：计算步骤s1模糊推理输出的动作变量，对动作变量再次进行模糊推理；
8.s3：结合两次模糊推理结果，根据q值大小，再利用sarsa(λ)训练出机器人在相应规则下所要采取的动作。
9.进一步地，步骤s1中，将测量的障碍物距离转换为有限的规则的具体步骤如下：
10.s11：用机器人前部的三个超声波传感器分别测量出机器人自身和机器人前方三个障碍物的距离信息；
11.s12：利用隶属度函数对距离信息进行模糊化处理，隶属度函数为：
[0012][0013]
每个障碍物的距离都对应近，中，远三个隶属度，于是三个障碍物距离信息可以转化为27个规则。式中x为障碍物距离，f(x)为隶属度。
[0014]
进一步地，步骤s2中，计算输出的动作变量并对动作变量再次进行模糊推理的具体步骤如下：
[0015]
s21：根据超声波传感器到障碍物的距离信息计算被激活的规则的激活度如下：
[0016][0017]
式中，μ(x1)，μ(x2)，μ(x3)分别为三个障碍物距离模糊化处理后的隶属度；
[0018]
s22：六足机器人转动的空间取[
‑
60
°
，60
°
]；向右转取正，直行取0，左转取负；然后平均划分为五个离散动作，取
‑
60
°
，
‑
30
°
，0
°
，30
°
，60
°
；
[0019]
s23：测量距离会在27个规则中激活多个规则(激活度不为0)，根据q值(初始化为0)的大小，用动作选择策略ε
‑
greedy从5个离散动作中选择一个动作，称为激活动作，用表示,j代表第几个规则；
[0020]
s24：将从所有激活规则所选出的激活动作与被激活的规则的激活度相乘并求和，得到距离信息为x时的连续动作变量c(x)：
[0021][0022]
式中，为第r个规则的激活度；
[0023]
s25：将c(x)再次进行模糊化处理，模糊语言分为{lb,ls，z，rs，rb}＝{“左大”，“左小”，“零”，“右小”，“右大”}，论域范围是[
‑
60
°
，60
°
]，隶属度函数采用三角形函数,其中“左大”所对应的论域范围为[
‑
60
°
，
‑
30
°
]，“左小”所对应的论域范围为[
‑
60
°
，0
°
]，其中“零”所对应的论域范围为[
‑
30
°
，30
°
]，“右小”所对应的论域范围为[0
°
，60
°
]，其中“右大”所对应的论域范围为[30
°
，60
°
]。
[0024]
第r条规则所对应的q值分量为：
[0025][0026]
式中，σ
r
，
j
(c(x))为c(x)模糊化处理后的隶属度，q
r，j
为第r条规则下对应的第j个q值。
[0027]
进一步地，步骤s3中，利用sarsa(λ)训练出机器人在相应规则下所要采取的动作
的具体步骤如下：
[0028]
s31：根据所求的q
r
(x，c(x))，可以得到执行连续动作c(x)时的q值：
[0029]
令
[0030][0031][0032]
则
[0033][0034]
s32：根据sarsa算法更新q值：
[0035]
q
t+1
＝q
t
+α[r+γq(x
t+1
，u
t+1
)
‑
q(x
t
，u
t
)]e
t
ꢀꢀꢀ
(8)
[0036]
其中α是步长参数，u
t
为t时刻测得的三个距离推理得出的动作变量，γ是折扣因子，q
t
为t时刻的q值向量，e
t
是t时刻的资格迹向量：q(x
t
，u
t
)为步骤s31中计算出的q值；
[0037][0038]
式中，e
t
(r,j)为对应于q
r,j
的资格迹元素，λ的取值范围为[0,1]；
[0039]
s33：训练完毕，选择最大q值对应的动作作为模糊规则的后件部分，得到完备的模糊规则库。
[0040]
本发明的有益效果在于：本发明采用模糊sarsa(λ)的方法，可以很好的解决强化学习难以利用与连续状态的问题，也可以有效的解决模糊控制中模糊推理机制建立复杂的问题。
[0041]
通过模糊推理将距离信息转化为一个有限的状态集合，然后经过第一层模糊推理之后得到机器人需要进行的动作，之后再对动作进行第二层模糊推理，之后融合两次模糊推理结果更新资格迹，可以加快sarsa算法的收敛速度。
附图说明
[0042]
图1为本发明具体实施例的六足机器人模型图；
[0043]
图2为本发明具体实施例的六足机器人关节执行器结构图；
[0044]
图3为六足机器人cpg步态图；
[0045]
图4为本发明的方法框图；
[0046]
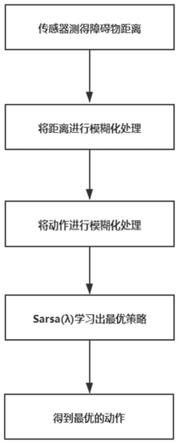
图5为本发明方法流程图。
具体实施方式
[0047]
为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。
[0048]
相反，本发明涵盖任何由权利要求定义的在本发明的精髓和范围上做的替代、修改、等效方法以及方案。进一步，为了使公众对本发明有更好的了解，在下文对本发明的细节描述中，详尽描述了一些特定的细节部分。对本领域技术人员来说没有这些细节部分的描述也可以完全理解本发明。
[0049]
本发明的方法适用的硬件结构以图1所示的具体实施例进行说明，本方法可以应用于各类移动机器人，本实施例的六足机器人身体前方带有三个超声波传感器，用来进行机器人和前方三个障碍物之间距离的测量。
[0050]
六足机器人运动系统中，由18个串联弹性执行器组成，图2为执行器的结构图，执行器驱动电机为无刷直流电机，电机驱动方法为六步换向法，逆变电路由多个开关元件(mosfet等)进行电桥连接，用来将直流电源所提供的直流电转换为驱动无刷直流电机的交流电。位置、速度、力矩传感器由多个编码器组成，编码器u2主要用来计算输出位置及速度、编码器u1和编码器u2的差值信号主要用来计算输出力矩；减速器使用齿轮减速箱；弹性元件安装于减速器输出端以及执行器的输出法兰之间，编码器u2与编码器u1分别安装在弹性元件前后，用于形变量的检测，同时编码器u2还负责输出位置和速度的检测。
[0051]
六足机器人的每条腿有三个自由度，总共18个自由度，每个自由度由一个执行器控制，机器人的步态主要有三足步态、波浪步态、转弯步态。六足机器人的各种步态采用cpg方法生成，cpg由六个hopf振荡器组成全对称耦合，耦合方式见图3，每一个振荡器对应一条腿的髋关节，然后生成的信号经过映射函数的映射之后输出给每条腿的各个关节，得到输出的最佳动作之后六足机器人通过cpg生成的步态进行行走。
[0052]
操作系统采用ros操作系统，在gazebo软件中建立机器人的避障模型，把避障过程转换为一个马尔科夫决策过程，通过传感器测量的距离，将之进行模糊化处理，然后利用sarsa(λ)算法学习出机器人在相应的状态下所要采取的最佳动作。
[0053]
如图4所示，本发明提供了一种基于双层模糊强化学习的六足机器人避障方法，该方法包括如下步骤：
[0054]
s1：六足机器人前方装有三个超声波传感器，通过超声波传感器测量自身和障碍物之间的距离，并将三个超声波传感器分别测得的三个障碍物的距离进行模糊推理，将测量的连续的距离转换为离散的有限的状态，每个状态即为一个模糊规则；具体步骤如下：
[0055]
s11：用机器人前部的三个超声波传感器分别测量出机器人自身和机器人前方三个障碍物的距离信息；
[0056]
s12：利用隶属度函数对距离信息进行模糊化处理，隶属度函数为：
[0057][0058]
每个障碍物的距离都对应近，中，远三个隶属度，于是三个障碍物距离信息可以转化为27个规则。式中x为障碍物距离，f(x)为隶属度。
[0059]
s2：计算步骤s1模糊推理输出的动作变量，对动作变量再次进行模糊推理；具体步骤如下：
[0060]
s21：根据超声波传感器到障碍物的距离信息计算被激活的规则的激活度如下：
[0061][0062]
式中，μ(x1)，μ(x2)，μ(x3)分别为三个障碍物距离模糊化处理后的隶属度；
[0063]
s22：六足机器人转动的空间取[
‑
60
°
，60
°
]；向右转取正，直行取0，左转取负；然后平均划分为五个离散动作，取
‑
60
°
，
‑
30
°
，0
°
，30
°
，60
°
；
[0064]
s23：测量距离会在27个规则中激活多个规则(激活度不为0)，根据q值(初始化为0)的大小，用动作选择策略ε
‑
greedy从5个离散动作中选择一个动作，称为激活动作，用表示,j代表第几个规则；
[0065]
s24：将从所有激活规则所选出的激活动作与被激活的规则的激活度相乘并求和，得到距离信息为x时的连续动作变量c(x)：
[0066][0067]
式中，为第r个规则的激活度；
[0068]
s25：将c(x)再次进行模糊化处理，模糊语言分为{lb,ls，z,rs，rb}＝{“左大”，“左小”，“零”，“右小”，“右大”}，论域范围是[
‑
60
°
，60
°
]，隶属度函数采用三角形函数,其中“左大”所对应的论域范围为[
‑
60
°
，
‑
30
°
]，“左小”所对应的论域范围为[
‑
60
°
，0
°
]，其中“零”所对应的论域范围为[
‑
30
°
，30
°
]，“右小”所对应的论域范围为[0
°
，60
°
]，其中“右大”所对应的论域范围为[30
°
，60
°
]。
[0069]
第r条规则所对应的q值分量为：
[0070][0071]
式中，σ
r，j
(c(x))为c(x)模糊化处理后的隶属度，q
r，j
为第r条规则下对应的第j个q值。
[0072]
s3：结合两次模糊推理结果，根据q值大小，再利用sarsa(λ)训练出机器人在相应规则下所要采取的动作。具体步骤如下：
[0073]
s31：根据所求的q
r
(x，c(x))，可以得到执行连续动作c(x)时的q值：
[0074]
令
[0075][0076]
[0077]
则
[0078][0079]
s32：根据sarsa算法更新q值：
[0080]
q
t+1
＝q
t
+α[r+γq(x
t+1
，u
t+1
)
‑
q(x
t
，u
t
)]e
t
ꢀꢀꢀ
(8)
[0081]
其中α是步长参数，u
t
为t时刻测得的三个距离推理得出的动作变量，γ是折扣因子，q
t
为t时刻的q值向量，e
t
是t时刻的资格迹向量：q(x
t
，u
t
)为步骤s31中计算出的q值；
[0082][0083]
式中，e
t
(r，j)为对应于q
r，j
的资格迹元素，λ的取值范围为[0,1]；
[0084]
s33：训练完毕，选择最大q值对应的动作作为模糊规则的后件部分，得到完备的模糊规则库。