基于改进play算子的电机伺服控制系统迟滞控制方法

1.本发明涉及电机控制器技术领域，尤其涉及一种基于改进play算子的电机伺服控制系统迟滞控制方法。


背景技术：

2.现有的超声波电机伺服控制系统的设计中，当速度跟踪周期性信号时，其力矩
‑
速度的关系呈现滞回特性，因此跟踪同一个信号在上升和下降区间有一定的误差。一般play算子只能补偿较为简单的滞回特性。中国专利201710223807提出了一种基于stop算子的超声波电机伺服控制系统对称滞回控制方法，但在进一步研究中发现，该种控制方法可以补偿的迟滞特性种类有限，而且运算量过大，模型过于复杂，实际使用需要较快的处理器和存储器，需要进一步改进和优化。


技术实现要素：

3.现有的超声波电机伺服控制系统的设计中由于力矩输出处于合适状态时，其滞回具有对称性，对周期重复信号控制时有一定的误差。为了改善跟随性能的精确性，本发明设计了基于改进play算子对称补偿控制的超声波电机伺服控制方案。基于改进play算子能有效增进系统的控制效能，提升控制系统对迟滞的精确性，并进一步减少系统对于不确定性的影响程度，电机的力矩与速度控制可以获得较好的重复特性。
4.本发明具体采用以下技术方案：
5.一种基于改进play算子的电机伺服控制系统迟滞控制方法，其特征在于：
6.采用的对称滞回补偿控制基于超声波电机驱动系统的动态方程：
[0007][0008]
其中a
p
＝
‑
b/j,b
p
＝j/k
t
＞0,c
p
＝
‑
1/j；b为阻尼系数，j为转动惯量，k
t
为电流因子，t
f
(v)为摩擦阻力力矩，t
l
为负载力矩，u(t)是电机的输出力矩，θ
r
(t)为通过光电编码器测量得到的位置信号；
[0009]
当电机的负载力矩适中时，电机力矩
‑
速度特性的迟滞具有对称性，为了减少此现象造成的影响同时减少运算量，使用改进广义play算子对迟滞对其进行补偿控制；
[0010]
假设0＝t0＜t1＜
…
t
n
＝t
e
为[0,t
e
]的一个区间，v(t)为输入信号，f
m
γ
r
[v](t)为迟滞系统的输出信号；输入函数v在每一个[t
i
,t
i+1
]区间内是单调的，任何输入v(t)∈c
e
[0，t
e
]，改进的广义play算子阈值r定义为：
[0011][0012][0013][0014]
其中t
i
＜t≤t
i+1
，0≤i≤n
‑
1，max表示二数比较取最大，min表示二数比较取最小；
γ
l
(v
‑
r)和γ
r
(v+r)为两个严格增长的包络函数，改进的广义play算子迟滞形状受两个包络函数限制；改进的广义play算子阈值的解为：γ
l
(v
‑
r)＝0，γ
r
(v+r)＝0，分别对应和改进的广义play算子的边界是沿gx/v(t)轴平移的包络函数γ[v]，包络函数γ[v]的形状和边界相同；
[0015]
π
m
[v](t)模型定义为改进广义play算子的加权积分，即
[0016][0017]
其中p0是一个正常数，表示当r＝0时改进广义play算子p(r)是密度函数；π
m
[v](t)模型对任何给定输入v(t)∈c
m
[0，t
e
]是lipschitz连续；r为阈值r的上限值。
[0018]
进一步地，基于初始负荷曲线φ和逆模型的负荷曲线对称，得到
[0019][0020]
初始负荷曲线φ表示为：
[0021][0022]
其中，γ(r)为输入函数，根据输入数据范围选择包络函数γ
l
(r)和γ
r
(r)的其中一个；θ是积分变量，积分范围是[0，r]；当选择包络函数γ[v]时，线性函数γ[v]＝v；
[0023]
π
m
[v](t)模型解析逆如下所示，
[0024][0025]
其中g0是正常数，g(r)是密度函数，β是包络函数，是具有阈值q和包络函数β的改进的广义play算子；q为阈值q的上限值；
[0026]
逆模型的负荷曲线的加载曲线为：
[0027][0028]
其衍生公式，
[0029][0030]
是对时间的导数，同理β'(q)、β'(r
‑
η)是β(q)、β(r
‑
η)对时间的导数。这两条加载曲线的导数代入式(6)，得到，
[0031][0032]
及
[0033]
β[v]＝γ
‑1[v]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(12)
[0034]
π
m
[v](t)模型的逆写成：
[0035][0036]
是p0的逆，通过式(6)得到密度函数g(q)
[0037][0038]
进一步地，将迟滞描述为n个算子之和，则π
m
[v](t)模型写成，
[0039][0040]
其中n是改进的广义play算子的数量，r
i
是第i个阈值，r满足0＝r0<r1<
···
<r
n
＝r。
[0041]
进一步地，将迟滞描述为n个算子之和，则π
m
[v](t)逆模型写成，
[0042][0043]
其中n是改进的广义play算子的数量，q
i
是第i个阈值满足0＝q0<q1<...<q
n
＝q；
[0044]
在逆模型中需要计算的参数有g0，β[v]，q
i
和g(q
i
)；因此，初始加载曲线及其逆r∈[r
j
,r
j+1
)和q∈[q
j
,q
j+1
)记为：
[0045][0046][0047]
r∈[r
j
,r
j+1
)和q∈[q
j
,q
j+1
)加载曲线的导数为：
[0048][0049][0050]
由式(6)得到：
[0051][0052]
从而有：
[0053][0054]
及
[0055]
β[v]＝γ
‑1[v]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(21)
[0056]
逆模型算子的阈值为：
[0057][0058]
再次使用公式(6)得，
[0059]
[0060]
逆模型的密度函数g(q
j
)为
[0061][0062]
因此用给定的模型，其逆可以按照以上步骤实现。
[0063]
由稳定性理论可以证明，上述系统是稳定的。使用补偿控制使得系统力矩速度的特性接近线性关系。
[0064]
以及，一种超声波电机伺服控制系统，其特征在于，采用如上所述的基于改进play算子的电机伺服控制系统迟滞控制方法进行滞回补偿控制，包括基座和设于基座上的超声波电机；所述超声波电机一侧输出轴与光电编码器相连接，另一侧输出轴与飞轮惯性负载相连接；所述飞轮惯性负载的输出轴经联轴器与力矩传感器相连接；所述光电编码器的信号输出端、所述力矩传感器的信号输出端分别接至控制系统。
[0065]
进一步地，所述控制系统包括超声波电机驱动控制电路，所述超声波电机驱动控制电路包括控制芯片电路和驱动芯片电路，所述光电编码器的信号输出端与所述控制芯片电路的相应输入端相连接，所述控制芯片电路的输出端与所述驱动芯片电路的相应输入端相连接，以驱动所述驱动芯片电路，所述驱动芯片电路的驱动频率调节信号输出端和驱动半桥电路调节信号输出端分别与所述超声波电机的相应输入端相连接。
[0066]
进一步地，整个控制器的系统建立在改进play算子对滞回数学模型进行处理，在减小辨识动态误差的同时也使得伺服系统滞回最小。在减小辨识动态误差的同时也使得伺服系统滞回最小，从而能获得更好的输入输出控制效能。
[0067]
进一步地，所述控制系统的硬件电路包括超声波电机驱动控制电路，所述超声波电机驱动控制电路包括控制芯片电路和驱动芯片电路，所述光电编码器的信号输出端与所述控制芯片电路的相应输入端相连接，所述控制芯片电路的输出端与所述驱动芯片电路的相应输入端相连接，以驱动所述驱动芯片电路，所述驱动芯片电路的驱动频率调节信号输出端和驱动半桥电路调节信号输出端分别与所述超声波电机的相应输入端相连接。
[0068]
进一步地，所述联轴器为弹性联轴器。
[0069]
进一步地，所述超声波电机、光电编码器、力矩传感器分别经超声波电机固定支架、光电编码器固定支架、力矩传感器固定支架固定于所述基座上。
[0070]
与现有技术相比，本发明及其优选方案基于改进play算子对称补偿控制能有效增进系统的控制效能，并进一步减少系统对于不确定性的影响程度，电机的力矩与速度控制可以获得较好的动态特性。
附图说明
[0071]
下面结合附图和具体实施方式对本发明进一步详细的说明：
[0072]
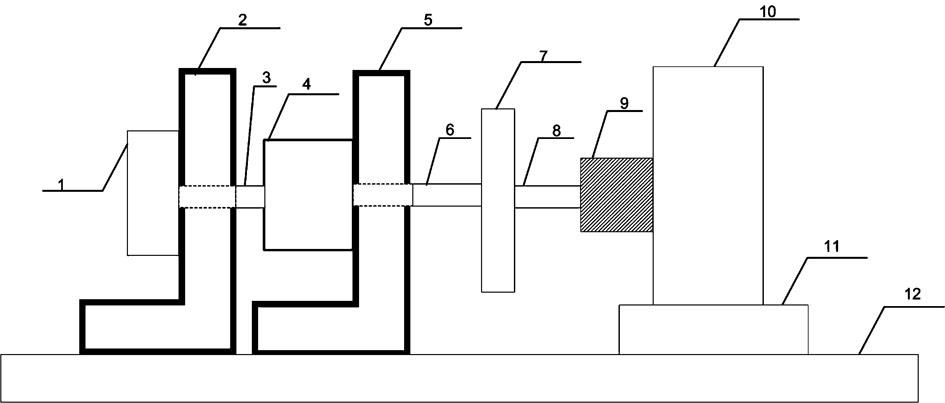
图1是本发明实施例超声波电机伺服控制系统示意图；
[0073]
图2是本发明实施例控制电路原理示意图。
[0074]
图中，1
‑
光电编码器，2
‑
光电编码器固定支架，3
‑
超声波电机输出轴，4
‑
超声波电
机，5
‑
超声波电机固定支架，6
‑
超声波电机输出轴，7
‑
飞轮惯性负载，8
‑
飞轮惯性负载输出轴，9
‑
弹性联轴器，10
‑
力矩传感器，11
‑
力矩传感器固定支架，12
‑
基座，13
‑
控制芯片电路，14
‑
驱动芯片电路，15、16、17
‑
光电编码器输出的a、b、z相信号，18、19、20、21
‑
驱动芯片电路产生的驱动频率调节信号，22
‑
驱动芯片电路产生的驱动半桥电路调节信号，23、24、25、26、27、28
‑
控制芯片电路产生的驱动芯片电路的信号，29
‑
超声波电机驱动控制电路。
具体实施方式
[0075]
为让本专利的特征和优点能更明显易懂，下文特举实施例，并配合附图，作详细说明如下：
[0076]
本实施例采用的超声波电机控制系统，如图1所示，包括基座12和设于基座12上的超声波电机4，所述超声波电机4一侧输出轴3与光电编码器1相连接，另一侧输出轴6与飞轮惯性负载7相连接，所述飞轮惯性负载7的输出轴8经弹性联轴器9与力矩传感器10相连接，所述光电编码器1的信号输出端、所述力矩传感器10的信号输出端分别接至控制系统。
[0077]
上述超声波电机4、光电编码器1、力矩传感器10分别经超声波电机固定支架5、光电编码器固定支架2、力矩传感器固定支架11固定于所述基座12上。
[0078]
如图2所示，上述控制系统包括超声波电机驱动控制电路29，所述超声波电机驱动控制电路29包括控制芯片电路13和驱动芯片电路14，所述光电编码器1的信号输出端与所述控制芯片电路13的相应输入端相连接，所述控制芯片电路13的输出端与所述驱动芯片电路14的相应输入端相连接，以驱动所述驱动芯片电路14，所述驱动芯片电路14的驱动频率调节信号输出端和驱动半桥电路调节信号输出端分别与所述超声波电机4的相应输入端相连接。所述驱动芯片电路14产生驱动频率调节信号和驱动半桥电路调节信号，对超声波电机输出a、b两相pwm的频率、相位及通断进行控制。通过开通及关断pwm波的输出来控制超声波电机的启动和停止运行；通过调节输出的pwm波的频率及两相的相位差来调节电机的最佳运行状态。
[0079]
在本实施例中，整个控制器的系统建立在改进play算子对滞回数学模型进行处理，在减小辨识动态误差的同时也使得伺服系统滞回最小，从而能获得更好的输入输出控制效能。
[0080]
超声波电机驱动系统的动态方程可以写为：
[0081][0082]
其中a
p
＝
‑
b/j,b
p
＝j/k
t
＞0,c
p
＝
‑
1/j；b为阻尼系数，j为转动惯量，k
t
为电流因子，t
f
(v)为摩擦阻力力矩，t
l
为负载力矩，u(t)是电机的输出力矩，θ
r
(t)为通过光电编码器测量得到的位置信号。
[0083]
当电机的负载力矩适中时，电机力矩
‑
速度特性的迟滞具有对称性，为了减少此现象造成的影响同时减少运算量，我们使用改进广义play算子对迟滞对其进行补偿控制。
[0084]
假设0＝t0＜t1＜
…
t
n
＝t
e
为[0,t
e
]的一个区间，v(t)为输入信号，为迟滞系统的输出信号。输入函数v在每一个[t
i
,t
i+1
]区间内是单调的，任何输入v(t)∈c
e
[0，t
e
]，改进的广义play算子阈值r定义为：
[0085][0086][0087][0088]
其中t
i
＜t≤t
i+1
，0≤i≤n
‑
1，max表示二数比较取最大，min表示二数比较取最小。
[0089]
γ
l
(v
‑
r)和γ
r
(v+r)为两个严格增长的包络函数，改进的广义play算子迟滞形状受两个包络函数限制。改进的广义play算子阈值的解就是γ
l
(v
‑
r)＝0，γ
r
(v+r)＝0，它们分别是和如果选择γ(0)＝0，改进广义play算子的阈值为
±
r。此外，改进广义play算子的边界是沿gx/v(t)轴平移的包络函数γ[v]，包络函数γ[v]的形状和边界相同。
[0090]
π
m
[v](t)模型定义为改进广义play算子的加权积分，即：
[0091][0092]
其中p0是一个正常数，表示当r＝0时改进广义play算子p(r)是密度函数。π
m
[v](t)模型对任何给定输入v(t)∈c
m
[0，t
e
]是lipschitz连续。
[0093]
基于初始负荷曲线φ和逆模型的负荷曲线对称，得到：
[0094][0095]
负荷曲线φ可以表示为：
[0096][0097]
γ(r)为输入函数，当选择包络函数γ[v]时，线性函数γ[v]＝v。
[0098]
π
m
[v](t)模型解析逆如下所示：
[0099][0100]
其中g0是正常数，g(r)是密度函数，β是包络函数，是具有阈值q和包络函数β的改进的广义play算子。
[0101]
负荷曲线的加载曲线为
[0102][0103]
其衍生公式，
[0104][0105]
这两条加载曲线的导数代入(6)，可以得到，
[0106][0107]
及
[0108]
β[v]＝γ
‑1[v]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(12)
[0109]
π
m
[v](t)模型的逆可以写成：
[0110]
[0111]
用(6)可以得到密度函数g(q)，
[0112][0113]
在实际应用中，迟滞可以近似地描述为n个算子之和。因此，π
m
[v](t)模型可以写成，
[0114][0115]
其中n是改进的广义play算子的数量，r
i
是第i个阈值，r满足0＝
[0116]
r0<r1<
···
<r
n
＝r，且π
m
[v](t)逆模型写成：
[0117][0118]
其中n是改进的广义play算子的数量，q
i
是第i个阈值满足0＝q0<q1<...<q
n
＝q。在逆模型中需要计算的参数有g0，β[v]，q
i
和g(q
i
)。因此，初始加载曲线及其逆r∈[r
j
,r
j+1
)和q∈[q
j
,q
j+1
)记为：
[0119][0120][0121]
r∈[r
j
,r
j+1
)和q∈[q
j
,q
j+1
)加载曲线的导数为：
[0122][0123][0124]
由(4
‑
12)得到
[0125][0126]
从而
[0127][0128]
及
[0129]
β[v]＝γ
‑1[v]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(21)
[0130]
逆模型算子的阈值为：
[0131]
[0132]
再次使用(6)得，
[0133][0134]
逆模型的密度函数g(q
j
)为：
[0135][0136]
因此用给定的模型，其逆可以按照以上步骤实现。
[0137]
由稳定性理论可以证明，上述系统是稳定的。使用补偿控制使得系统力矩速度的特性接近线性关系。
[0138]
本专利不局限于上述最佳实施方式，任何人在本专利的启示下都可以得出其它各种形式的基于改进play算子的电机伺服控制系统迟滞控制方法，凡依本发明申请专利范围所做的均等变化与修饰，皆应属本专利的涵盖范围。