轮胎-路面附着系数与轮胎侧偏角的估计方法与流程

本发明涉及一种车辆安全性测试技术，特别涉及一种基于非线性滑模观测器的轮胎-路面附着系数与轮胎侧偏角的估计方法。

背景技术：
车辆稳定性控制一直是车辆主动安全性研究的热点，一般而言，各种驾驶辅助系统与主动安全产品实现其功能，都需要轮胎与路面接触相互作用的信息，其中关键参数是轮胎-路面接触的附着系数和轮胎的侧偏角。若已知附着系数与轮胎侧偏角等信息，根据轮胎数学模型就能推算出轮胎与路面接触产生的相互作用力。然后设计不同的控制算法，实现各种车辆稳定性控制的功能。目前工程中虽有能够直接测量轮胎路面附着系数的传感器，但是受限于传感器成本、测量精度以及测量稳定性较差等原因，无法在量产车中推广使用。因此，在设计车辆稳定性控制系统时，一种方式是通过实验获得附着系数与相关参数之间的确定性关系，利用可测信息推算附着系数，例如在ABS系统中，先确定滑移率与附着系数关系曲线，利用已知的滑移率来计算附着系数。这种方式有其一定的适用性，但实验中获得的数据是在特定条件下获得，而影响轮胎-路面附着特性的因素很多，因此运用这种方式，在外部环境改变时，就很难得到准确的附着系数。另一种方式是采用估计的方式获得附着系数。现有的方法大至可分为：检测道路表面情况，基于激励(cause-based)的方法,例如运用视觉、温度传感器，检测道路表面积水、冰或是雪地路面，间接获得附着系数；另一种，称之为基于运动响应效果(effect-based)的方法,这种方法运用车辆、轮胎的动力学特性，推导路面附着系数与车辆运动行为的关系，通过现有的车辆控制系统硬件（例如EPS、ABS、AFS等）来获取车辆运动参数，利用相关算法估计附着系数。轮胎力与路面附着系数同时与一些无法控制的环境因素密切相关，例如气温，胎面磨损情况，垂向载荷，胎压等。往往这些环境因素难以检测，基于激励的方法无法将这些因素的影响表现出来。同时，相比后者能够从现有系统获取需要的车辆运动状态信息而言，基于激励的方法需要额外增设检测设备，检测成本相对较高。因此，现在的路面附着系数估计的研究更多倾向于基于效果的方法。

技术实现要素：
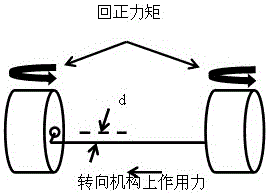
本发明是针对现在车辆主动安全性研究中轮胎-路面附着特性难测量并且运动信息提取费用高的问题，提出一种轮胎-路面附着系数与轮胎侧偏角的估计方法，以非线性滑模观测器和轮胎回正模型为基础，以鲁棒稳定性为设计指标，能够保证系统获得准确的轮胎-路面附着系数和轮胎侧偏角估计值。本发明的技术方案为：一种轮胎-路面附着系数与轮胎侧偏角的估计方法，具体包括如下步骤：1）建立车辆动力学模型；2）选择轮胎回正模型，通过转向机构模型推导出轮胎自回正力矩数学模型；3）设计滑模观测器方程如下：式中是观测器增益矩阵，为状态估计值，为系统输入，为估计输出值，为测量值与估计值之差，为符号函数；设系统的状态为：,输出是，为轮胎侧偏角，为路面附着系数，为侧向加速度，为总回正力矩，将系统状态代入到步骤1），在其硬件平台的基础上，由侧向加速度传感器得到，可由步骤2）中的自回正力矩数学模型推算出；4）选择合适的观测器增益矩阵，将设计的滑模观测器代入系统，与的测量值与估算值差为误差系统，误差系统趋于零对轮胎-路面附着系数和轮胎侧偏角进行估计。所述步骤1）车辆动力学模型采用单轨车辆模型，建立车辆侧向及横摆运动的动力学方程：轮胎侧偏角运动学方程：其中，为整车质量，、为质心到前后轴的距离，为侧向加速度，和分别为纵向车速和侧向车速，为质心车速，、为前后轮质心速度，、、和分别为前后轮胎的纵向力和侧向力，为横摆转动惯量，和为横摆角速度和质心侧偏角，和为前后轮侧偏角，为前轮转角。所述步骤2）中轮胎回正模型为Fiala刷子轮胎模型，轮胎的非线性特征为其中，，，，为轮胎侧向力，为轮胎回正力矩，c为车轮与地面接触长度的一半，为轮胎侧偏角，为附着系数，为轮胎垂载荷，为轮胎侧偏刚度；自回正力矩用惯性-阻尼数学模型来描述：其中、和分别为方向盘转角，转角速度和角加速度，为转向机构有效转动惯量，为转向机构有效阻尼，为总回正力矩，为齿轮齿条上的作用力，d为相应力臂长度，即从主销中轴线到齿轮齿条的垂向距离。车辆动力学模型采用单轨车辆模型，所述步骤3）中滑模观测器为非线性滑模观测器，滑模观测器如下：其中为观测器滑模增益，取值范围如下：为消除抖振影响，定义函数取代符号函数，参数用于调节函数的斜率，和分别为前后轮胎的纵向力和侧向力的误差，、、、、和分别为对应的估计值。本发明的有益效果在于：本发明轮胎-路面附着系数与轮胎侧偏角的估计方法，可以对轮胎路面附着系数和轮胎侧偏角进行在线估计，非线性滑模观测器对于系统模型不确定性和测量扰动具有一定的鲁棒性，仿真实验得到的结果验证观测器算法的可行性，保证系统获得准确的轮胎-路面附着系数和轮胎侧偏角估计值。附图说明图1为二自由度单轨车辆动力学模型图；图2为转向机构模型图；图3为本发明滑模观测器中函数和示意图；图4为本发明仿真后侧偏角、附着系数的估计值与参考值比较图。具体实施方式如图1所示二自由度单轨车辆动力学模型图，采用车辆系统动力学研究中常用的单轨车辆模型，可以表征车辆系统的运动特性。建立车辆侧向及横摆运动的动力学方程，具体方程如下：(1)在轮胎侧偏角不大时根据简单的运动学关系可知：(2)(3)其中，为整车质量，、为质心到前后轴的距离，为侧向加速度，和分别为纵向车速和侧向车速，为质心车速，、为前后轮质心速度，、、和分别为前后轮胎的纵向力和侧向力，为横摆转动惯量，和为横摆角速度和质心侧偏角，和为前后轮侧偏角，为前轮转角。本发明采用Fiala刷子轮胎模型。它所需的参数较少，能较好表达轮胎的非线性特征，其表达式为(4)其中，，，，为轮胎侧向力，为轮胎回正力矩，c为车轮与地面接触长度的一半，为轮胎侧偏角，为附着系数，为轮胎垂载荷，为轮胎侧偏刚度。本文中选取单轨车辆模型，假定纵向速度一定，因此前后轮垂载荷为定值。轮胎回正力矩在行驶过程中不能直接测量。然而，方向盘转角，方向盘转矩都是可以测量的。如果存在助力机构或是主动前轮转向系统，其加载在转向机构上的力矩也是可以获得的。如图2所示转向机构模型示意图，自回正力矩可以用一个简单的惯性-阻尼数学模型来描述：(5)其中、和分别为方向盘转角，转角速度和角加速度。为转向机构有效转动惯量，为转向机构有效阻尼。为总回正力矩，为齿轮齿条上的作用力，d为相应力臂长度(即从主销中轴线到齿轮齿条的垂向距离)。滑模观测器是一类输入为估计输出和测量输出的误差的观测器，可以通过强制系统状态进入滑动模态来重构系统的状态，也继承了变结构控制固有的对参数不确定性、模型误差干扰的鲁棒性，同时，滑模观测器还具有计算量小、设计和实现简单等优点。设系统方程为：(6)为系统状态变量，为系统输入，为系统测量输出值。设计滑模观测器方程如下：(7)式中是观测器增益矩阵，为状态估计值，为估计输出值，为估计误差，为符号函数，为消除抖振影响，定义函数取代符号函数。(8)式中：为测量值与估计值之差；参数用于调节函数的斜率，如图3所示。针对现有的车辆稳定性控制系统，在其硬件平台的基础上，获取传感器信息，设计滑模观测器向控制系统提供更为准确的轮胎路面和附着系数估计值。所需的测量值为侧向加速度和总回正力矩，可由侧向加速度传感器得到，可由式（5）推算得到。设系统的状态为：,输出是，假定在较短的时间内车速保持恒定，则对式（2）求导可得，(9)结合式（1）、（3）和式（4），将其变换成如下：(10)其中，为路面附着系数测量值为侧向加速度和总回正力矩：(11)设计如下滑模观测器：(12)其中为观测器滑模增益。为分析观测器的收敛性，定义误差为，，误差系统为(13)取Lyapunov函数为(14)定义为(15)如果都小于零，Lyapunov函数，误差系统是稳定收敛的，误差，，则，。选择合适的滑模增益可使Lyapunov函数。增益具体设置如下：(16)收敛性证明(17)选择滑模增益如下：(18)代入上式可得(19)由于，可得到，因此，。同理，(20)选择滑模增益，，代入上式可得(21)由于，可得到，因此，。按照上述方法利用MATLAB/Simulink搭建观测器与Carsim汽车动力学仿真软件进行通信，搭建联合仿真平台。利用Carsim软件中的整车模型作为虚拟样车，采集实际中可以测量的信号作为观测器输入。本文选取D级乘用车，以车速100km/h行驶，两种轮胎-路面附着系数(0.8和0.4)，标准双移线工况进行仿真实验。观测器的输入信号选取车辆前轮信号，估计前后车轮侧偏角和轮胎与地面的附着系数。仿真结果如图4所示。由图可见所设计的非线性滑模观测器，可以对轮胎路面附着系数和轮胎侧偏角进行在线估计。观测器本身对于系统模型不确定性和测量扰动具有一定的鲁棒性。对两种不同附着系数路面进行操稳性仿真实验，得到的结果表明了观测器算法的可行性。