一种软件加速生命测试方法与流程

本发明涉及的是软件性能测试领域，具体涉及一种利用加速生命测试理论对产生老化现象的软件进行寿命测试的软件加速生命测试方法。

背景技术：
软件老化现象是软件长时间运行时，由于计算机资源的消耗而造成软件性能逐渐下降的现象。这种现象可能造成的后果是严重的，它不仅影响普通服务器软件的运行，并且可能对要求高可靠性的关键领域，如商业、金融、科技和军事等领域中使用的软件造成影响，在安全性要求极高的软件环境中，软件老化现象甚至可能造成人员伤害甚至生命损失。针对这种现象，学者提出了一种称作“软件再生(SoftwareRejuvenation)”的方法，也就是通过定期地重新启动服务器软件或者整个计算机系统，重新初始化服务器的内部状态，释放可能造成老化的被占用系统资源，使得软件的状态和性能得到恢复，从而避免或减缓老化造成的严重性能下降甚至软件系统宕机造成的损失。软件再生方法的应用当中，再生时间间隔的确定是一个非常重要的问题，若再生时间间隔选择过长，则可能不能避免软件老化现象造成的危害，若再生时间间隔选择过短，则主动再生行为本身为软件系统带来的开销就可能过大，造成软件实际使用效率的降低。通常，软件再生时间间隔会选择一个适当短于软件预期寿命的值，因此，对软件寿命的预测和估计一直是软件老化领域相关研究中的一个焦点。为了估计软件寿命的概率分布，可以对实际软件系统进行充分地抽象，利用马尔科夫模型、半马尔科夫模型、随机回报网、随机Petri网等数学模型对系统进行建模，从而抽象出软件寿命的特征；也可以研究真实的软件系统，利用各种性能参数的检测手段设计实验，从真实的实验中采集系统性能参数的各种变化数据，然后利用统计方法或者人工智能算法等，描述并且预测软件的寿命。对真实软件系统进行测试的一大障碍就是，通常情况下服务器软件都被设计成连续不间断地运行提供服务，即使存在老化现象，软件的寿命也会很长，很难直接通过实验得到软件失效时间的样本。传统的测试方式受制于测试时间和成本的限制，通常采用建立系统模型、预测模型或人工智能等方法，从较短时间的测试中采集适量性能数据，建模预测软件的寿命。

技术实现要素：
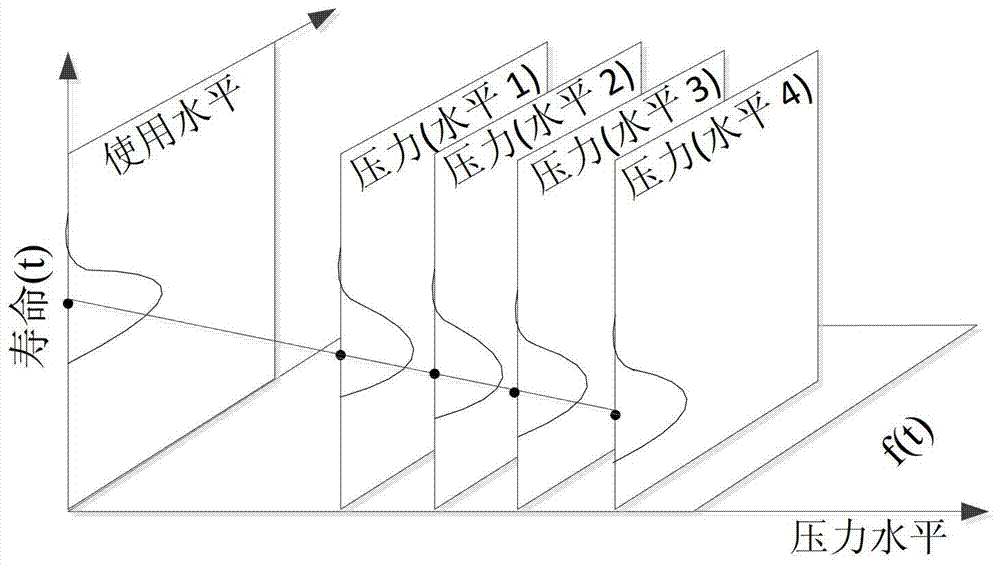
本发明的目的在于利用加速测试理论提供一种快速的测试手段，本发明的目的在于利用加速测试理论提供一种更快速推导出受到老化现象影响的软件在正常压力水平下的寿命的软件加速生命测试方法。本发明的目的是这样实现的：软件加速生命测试方法：（1）向服务器软件中的模块添加注入内存故障的代码，周期性调用模块使故障重复发生，在加速压力N的控制下发生内存泄漏；（2）分别设置加速水平的压力值N为4，8，12，16，在每个加速水平下重复运行程序7次，共进行28组测试；（3）记录每次发生内存泄漏即注入内存故障时的时间点即失效时间TTF，同时监测内存系统的内存使用情况，当内存量为零时，停止测试，保存数据；（4）根据数据计算内存消耗速率，估计软件寿命的样本分布，绘制每一加速压力水平下的寿命分布曲线，建立合适的寿命和压力之间的关系，估计非加速情况下被测试系统的平均失效时间MTTF的分布。添加注入内存故障的代码，在加速水平N的控制下发生内存泄漏，在第一次访问页面时，立即注入内存泄漏，即申请一片内存，保证内存在服务区软件重启之前不会释放，由于被申请的内存不能被回收，因此发生了内存泄漏，产生一个0到N之间的随机数，随机数决定了下次注入内存泄漏之前，页面还能够被正常访问的次数，每一次访问该页面，随机数减1，当随机数减为0时，注入一块新的内存泄漏，同时产生一个新的随机数，随机数服从均匀分布，注入内存泄漏的速度取决于这个页面被访问的频率和控制随机数上限的N值即加速压力水平。本发明的有益效果在于：本发明利用传统工业领域中已经得到了广泛应用的加速生命测试理论，部署和实施针对发生老化现象的软件的加速生命测试，通过耗时较短的加速生命测试得到加速情况下软件的寿命数据，计算非加速情况下软件的真实寿命，在更短的时间内，得到软件正常使用情况下寿命的概率分布。附图说明图1是本发明的执行流程示意图；图2是加速压力与寿命的关系示意图。具体实施方式下面结合附图对本发明做进一步描述：发明的目的在于利用加速测试理论提供一种快速的测试手段，设计一组耗时较短的加速实验，测试加速情况下软件的寿命数据，从而推导出受到老化现象影响的软件在正常压力水平下的寿命。这个目的可以按照以下步骤实现(如图1所示)：1.本发明的目的在于利用加速测试理论提供一种快速的测试手段，设计一组耗时较短的加速实验，测试加速情况下软件的寿命数据，从而推导出受到老化现象影响的软件在正常压力水平下的寿命。这个目的可以按照以下步骤实现：1.1待测试的对象应为服务器软件。1.2修改该服务器软件中的模块，添加注入内存故障的代码，使其能在加速压力N的控制下发生内存泄漏，其中该模块应能周期性地被调用，从而它内部存在的故障能重复发生。1.3分别设置加速水平的压力值N为4，8，12，16，然后在每个加速水平下重复运行程序7次，共28组实验。1.4在进行每组实验时，记录每次发生内存泄漏即注入内存故障时的时间点，同时用监测内存使用量的工具监测内存系统的内存使用情况，当监测工具显示内存量接近于零时，停止实验，保存并整理实验数据。1.5总共分析每次实验得到的在内存注入点上采集的数据，将最后一次成功注入之后，下一个失败的内存注入点为失效时间(TTF)，同时分析监测工具获取的内存占用量，用斜率估计方法计算内存消耗速率。1.6由于这些失效时间代表不同加速水平下被测系统的寿命样本值，因此从这些样本值中估计寿命样本的概率分布，如图2中每一加速压力水平下的寿命分布曲线。接下来，可以建立合适的寿命和压力之间的关系，如IPL-Weibull、IPL-Lognormal等，以利用加速和非加速情况下的压力水平，以及实验得到的加速情况下的失效时间样本，估计出非加速情况下被测试系统的平均失效时间(MTTF)的分布，如图2中正常压力水平下的寿命分布曲线。根据权利要求1所述的添加注入内存故障的代码，在加速水平N的控制下发生内存泄漏，其具体方法是：第一次访问该页面时，立即注入内存泄漏，也就是申请一片内存，而且这片内存在服务区软件重启之前不会释放。由于被申请的内存不能被回收，因此视为发生了内存泄漏，同时，产生一个0到N之间的随机数，随后，刚刚产生的随机数决定了下次注入内存泄漏之前，这个页面还能够被正常访问的次数。每一次访问这个页面，随机数都会减1，当随机数减为0时，就注入一块新的内存泄漏，同时产生一个新的随机数。由于随机数服从均匀分布，注入内存泄漏的速度取决于两个因素，一是这个页面被访问的频率，而是控制随机数上限的N。因此，N可视为加速压力水平。加速压力的选取可以根据具体软件的老化因素。当存在老化问题的软件中，老化相关的失效行为发生时，会造成软件内部的错误，并且引起性能的下降，这种失效的累积造成软件及其运行环境，如操作系统等资源的不断消耗，从而造成软件老化。例如，进程中内存管理程序错误可能造成内存泄漏问题，当这个错误的程序片段被反复调用时，内存泄漏故障就反复发生，不停地消耗系统可用的内存资源，从而造成系统性能的下降，最终可能导致系统因为内存耗尽而无法继续提供服务。这种情况下，内存使用情况是衡量软件老化程度的一个重要指标，可以使用内存消耗速率作为加速压力，通过为软件系统随机地人为注入内存泄漏，加速服务器软件的内存消耗速率来加速老化。关于加速测试计划的选取，根据加速理论，传统方式的测试计划通常为每个压力变量选择三到四个加速水平，每个加速水平上运行相同的测试次数。这种测试计划在较低的加速压力水平下得到的寿命估计值可能不精确，如果要求较高的精度，可以在较低压力水平下增加样本数。优化的测试计划只选择两个加速压力水平，一个高压力水平，一个低压力水平，而混合测试计划则是两种测试方式的折衷，通常也选择三到四个压力水平，但是在不同的加速压力水平下，测试样本数目并不相等。根据加速测试理论，在加速生命测试中，为了得到非加速情况下的软件寿命，需要使用的数学统计模型包括两个：一是寿命样本的概率分布，代表了被测系统寿命值的分散程度；二是寿命和压力之间的关系，通常，寿命的均值或者标准差是加速压力的函数。常用的用于表示寿命样本分布的概率分布包括指数分布(ExponentialDistribution)、正态分布(NormalDistribution)、指数正态分布(LognormalDistribution)以及Weibull分布等，而具体选择什么的分布则由实验获得的数据而定。例如，假设寿命数据(TTF)样本符合指数分布，则寿命t的概率密度函数为(1)：其中μ是被测系统寿命的期望。常见的寿命和压力关系函数包括Arrhenius关系、逆幂律(InversePowerLaw,IPL)关系等。以逆幂律为例，这是一种被广泛使用的寿命和压力关系函数，包括材料的耐电压测试、滚珠滚柱轴承测试、白炽灯寿命估计等。尽管许多时候寿命和压力关系并不是全局地遵循逆幂律，但是经验上，这种关系函数仍然可以描述许多产品的寿命特征。逆幂律代表的寿命和压力的关系模型可以用公式(2)表示：其中L表示被测系统的寿命特征，例如平均失效时间MTTF，s表示压力水平，k(k>0)和w是模型的参数，可以由测试中取得的失效样本估计出来。假定寿命数据(TTF)样本符合式(1)的指数分布，则联立式(1)与式(2)可以得到给定加速压力下TTF的分布，如式(3)所示：通过加速实验，可以获得几个不同加速水平下TTF值的样本集合。根据式(3)中给定加速压力水平下，被测系统平均寿命MTTF的概率分布，可以使用参数估计的方法，估计得到统平均失效时间MTTF，也就是L(s)的概率分布以及置信区间。实施例根据上述原理，下面通过一个实例说明如何实际部署加速生命测试来估计老化影响的软件的寿命。对于一个电子商务网站的Web服务器软件，发现其正常运行情况下，内存使用情况存在缓慢上升的趋势，并在一次约4.6天连续运行的记录中，测得其平均内存消耗速率约为0.0124kB/s。这表明该服务器软件可能存在内存泄露问题，在长期运行时可能发生老化现象，存在因为老化而性能下降或宕机的危险。为了评估该软件在正常使用情况下的寿命，选用内存使用速率作为加速因子，设计加速测试实验。为了引入人为的内存泄露现象，加速服务器内存泄露是速率，从而进行加速实验，可以在服务器中引入一个额外的模块，该模块在服务器正常处理HTTP请求时被随机调用，通过控制调用该模块的概率，设计了四个加速水平S1-S4(内存消耗速率的期望分别为149.61，82.518，58.132和47.321kB/s)，每个加速水平下进行七次重复实验，得到28组加速情况下的服务器寿命数据，如表1所示。对同一分组下的服务器寿命数据进行曲线拟合，发现其与Weibull分布的拟合程度较好，因此采用Weibull分布作为寿命的分布，如式(4)所示：其中β≥0为形状参数，η≥0为尺度参数。表1.加速生命测试得到的寿命样本(秒)选用逆幂律关系作为寿命-压力关系，从而可得IPL-Weibull概率密度函数如式(5)所示：从式(5)这个三参数模型中，可以解出被测系统在特定压力水平下平均失效时间MTTF的分布，如式(6)所示：其中Γ是伽马函数。通过加速测试数据，估计得到IPL-Weibull模型中参数β、k和w的值和置信区间，如表2所示。表2.IPL-Weibull模型的参数估计入正常水平下的内存消耗速率0.0124kB/s，可得非加速情况下MTTF的估计值为7.6115E+6秒，也就是126858分钟，其90%置信区间为(5.3730E+6,1.0782E+7)秒，也就是(89550,179700)分钟。