用于滑动轴承的轴承座或轴颈的结构强度计算方法和装置与流程

本发明涉及机械设备领域，具体地，涉及一种用于滑动轴承的轴承座或轴颈的结构强度计算方法和装置。

背景技术：

轴承是当代机械设备中的一种重要零部件。它的主要功能是支撑机械旋转，降低其运动过程中产生的摩擦，并保证其回转精度。在滑动轴承中，轴承座和轴颈在工作过程中的相互作用力称为轴承力。在对轴承座或轴颈进行结构设计时，可以通过轴承力来计算轴承座或轴颈的结构强度，再根据计算得到的结构强度改进结构设计。

目前，通常由轴系的动力学理论计算得到轴承座和轴颈之间相互作用的单一的集中力，将此集中力作为轴承力来计算结构强度。而滑动轴承在实际工作时，轴承座和轴颈之间具有一层润滑油膜，轴承力正是通过这层油膜进行传递的。因此，实际的轴承力是空间分布的力，上述集中力只是实际轴承力的近似。在油膜的作用下，轴承座和轴颈之间的作用力会分散到一个曲面上，根据由集中力计算得到的轴承座或轴颈的结构强度进行的相关结构设计往往是一种过设计，不仅导致材料的浪费，也有悖现代轻量化的设计原则。

技术实现要素：

本发明的目的是提供一种计算结果更加准确的滑动轴承的轴承座或轴颈的结构强度计算方法和装置。

为了实现上述目的，本发明提供一种用于滑动轴承的轴承座或轴颈的结构强度计算方法，所述方法包括：计算所述轴承座和所述轴颈之间相互作用的集中力；确定所述轴承座和所述轴颈之间相互作用的轴承力的分布函数；根据所述分布函数和所述集中力确定所述分布函数的参数值；以及根据所述分布函数和所述参数值计算所述轴承座或所述轴颈的结构强度。

优选地，所述确定所述轴承座和所述轴颈之间相互作用的轴承力的分布函数的步骤包括：根据雷诺方程确定所述轴承座和所述轴颈之间相互作用的轴承力的分布函数。

优选地，所述轴承力的分布函数为：所确定的轴承力在所述轴承座或所述轴颈的圆周方向上的120°圆心角所对应的圆弧范围内，呈余弦函数，并且，在所述轴承座或所述轴颈的轴线方向上的整个宽度范围内，呈余弦函数。

优选地，所述根据所述分布函数和所述集中力确定所述分布函数的参数值的步骤包括：根据所述分布函数确定所述轴承力的合力；以及在所述轴承力的合力等于所述集中力的情况下，计算所述分布函数的参数值。

本发明还提供一种用于滑动轴承的轴承座或轴颈的结构强度计算装置，所述装置包括：集中力计算模块，被配置为计算所述轴承座和所述轴颈之间相互作用的集中力；分布函数确定模块，被配置为确定所述轴承座和所述轴颈之间相互作用的轴承力的分布函数；参数值确定模块，被配置为根据所述分布函数和所述集中力确定所述分布函数的参数值；以及结构强度计算模块，被配置为根据所述分布函数和所述参数值计算所述轴承座或所述轴颈的结构强度。

通过上述技术方案，以更加接近于实际情况的空间分布力代替单一集中力来计算轴承座或轴颈的结构强度，使得计算得到的结构强度更加准确。由于空间分布的面力小于单一的集中力，因此本发明提供的用于滑动轴承的轴承座或轴颈的结构强度计算方法和装置避免了现有技术中对轴承座或轴颈的过设计问题，节约了制作材料。

本发明的其他特征和优点将在随后的具体实施方式部分予以详细说明。

附图说明

附图是用来提供对本发明的进一步理解，并且构成说明书的一部分，与下面的具体实施方式一起用于解释本发明，但并不构成对本发明的限制。在附图中：

图1是根据一示例性实施方式提供的用于滑动轴承的轴承座或轴颈的结构强度计算方法的流程图；

图2是根据一示例性实施方式提供的轴承座和轴颈沿垂直于转轴的平面的截面图；

图3a和图3b是一示例性实施方式提供的轴承座和轴颈之间相互作用的集中力的示意图；

图4a-图4c是根据一示例性实施方式提供的作用在轴承座上的轴承力的示意图；

图5a-图5c是根据一示例性实施方式提供的作用在轴颈上的轴承力的示意图；

图6是根据一示例性实施方式提供的确定分布函数的参数值的流程图；

图7是根据一示例性实施方式提供的用于滑动轴承的轴承座或轴颈的结构强度计算装置的结构框图；

图8是根据一示例性实施方式提供的参数值确定模块的结构框图。

具体实施方式

以下结合附图对本发明的具体实施方式进行详细说明。应当理解的是，此处所描述的具体实施方式仅用于说明和解释本发明，并不用于限制本发明。

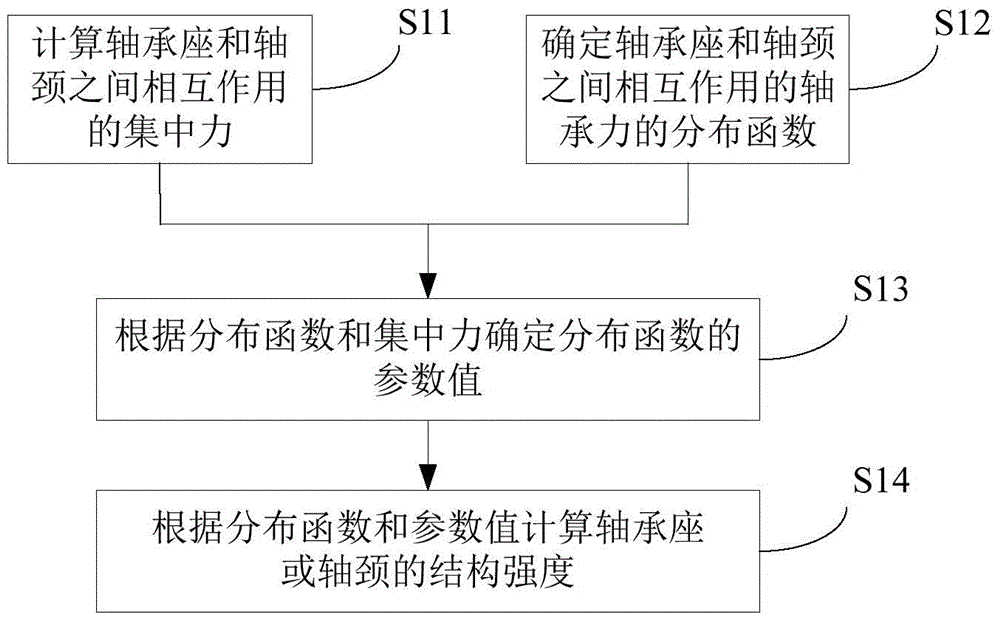
图1是根据一示例性实施方式提供的用于滑动轴承的轴承座或轴颈的结构强度计算方法的流程图。如图1所示，所述方法包括以下步骤。

在步骤s11中，计算轴承座和轴颈之间相互作用的集中力。

图2是根据一示例性实施方式提供的轴承座和轴颈沿垂直于转轴的平面的截面图。如图2所示，滑动轴承中，轴承座101和轴颈102之间填充有一层润滑油膜，当轴颈102在轴承座101中转动时，二者之间的轴承力正是通过这层油膜传递的。因为油膜的存在，实际的轴承力是复杂的空间分布力。

在相关技术中，通常由轴系动力学理论计算得到轴承座101和轴颈102之间相互作用的单一的集中力(作用在一个点上的作用力)。该集中力是实际轴承力(空间分布力)的近似。图3a和图3b是一示例性实施方式提供的轴承座101和轴颈102之间相互作用的集中力的示意图。如图3a和图3b所示，集中力为沿轴承座101或轴颈102的径向方向的力。轴承座101受到的集中力f的方向为从轴心指向轴承座101上的一点，轴颈102受到的集中力f'的方向为从轴颈102上的一点指向轴心。集中力f和集中力f'是作用力与反作用力，二者大小相等、方向相反。由轴系动力学理论计算集中力f和f'为本领域技术人员所公知，于此不再详细描述。

在步骤s12中，确定轴承座101和轴颈102之间相互作用的轴承力的分布函数。

本发明中所述的轴承力为空间分布力，即，轴承力为多个力的统称，并且轴承力的方向为沿着轴承座101或轴颈102的径向方向。如上所述，由于轴承座101和轴颈102之间填充有一层润滑油膜，二者之间实际的作用力为空间分布力，也就是作用在轴承座101或轴颈102上的面力。在该步骤s12中，轴承力的分布函数例如可以为轴承力的大小随着一角度(该角度用于表示轴承力的方向或作用点)的变化而变化的函数。

具体地，确定轴承座101和轴颈102之间相互作用的轴承力的分布函数(步骤s12)可以包括：根据雷诺方程确定轴承座101和轴颈102之间相互作用的轴承力的分布函数。其中，可以对雷诺方程采用差分法数值求解。该解法通过对轴承座101或轴颈102进行区域划分，形成网格。通过相邻点的差分式表示出方程的中的偏微分，从而通过迭代，使压力最终收敛，求得轴承座101或轴颈102各处所受压力。

以上求解雷诺方程所确定的轴承力的分布函数为：轴承力在轴承座101或轴颈102的圆周方向上的120°圆心角所对应的圆弧范围内，呈余弦函数，并且，在轴承座101或轴颈102的轴线方向上的整个宽度范围内，呈余弦函数。

具体地，图4a-图4c是根据一示例性实施方式提供的作用在轴承座101上的轴承力的示意图。图4a是轴承座101垂直于轴线的横截面图。如图4a所示，在轴承座101的圆周方向上，轴承力分布于170°-290°之间(120°圆心角)的圆弧范围内。如图4b所示，将轴承座101的圆周展开，在轴承座101的圆周方向上，轴承力呈余弦函数分布。如图4c所示，在轴承座101的轴线方向上，轴承力分布于轴承座101的整个宽度范围内，呈余弦函数分布。其中，h表示轴承力的最大值，即余弦函数前的系数。

图5a-图5c是根据一示例性实施方式提供的作用在轴颈102上的轴承力的示意图。图5a是轴颈102垂直于轴线的横截面图。如图5a所示，在轴颈102的圆周方向上，轴承力分布于170°-290°之间(120°圆心角)的圆弧范围内。如图5b所示，将轴颈102的圆周展开，在轴颈102的圆周方向上，轴承力呈余弦函数分布。如图5c所示，在轴颈102的轴线方向上，轴承力分布于轴颈102的整个宽度范围内，呈余弦函数分布。其中，h表示轴承力的最大值，即余弦函数前的系数。

如上所述，在图4a-图5c的实施方式中，轴承力分布在轴承座101或轴颈102的一个面上，方向沿径向。并且，轴承力呈对称分布，因此，在集中力f可看作是轴承力的合力的情况下，集中力f的作用点为轴承力的分布面上的中心点。图4a-图5c就是通过集中力f的作用点的截面上的示意图。其中，集中力f处于截面的中心。

这里需要说明的是，虽然使用了s11、s12这样的表述，但是并不意味着这两个步骤是有先后次序，这两个步骤可以是同时并行的。

在步骤s13中，根据分布函数和集中力确定分布函数的参数值。

分布函数表示出轴承力中的各个力的作用点(方向)，以及各个力之间的大小关系(例如，余弦函数关系)。要得到每个力的具体数值，还需要确定分布函数中的参数值(例如，余弦函数前的系数h)。在分布函数的基础上，再加上由轴系动力学得到的集中力f、以及集中力f与轴承力之间的合力关系，就能够确定轴承力的分布函数中的参数值。

具体地，图6是根据一示例性实施方式提供的确定分布函数的参数值的流程图。如图6所示，该步骤s13可以包括以下步骤。

在步骤s131中，根据分布函数确定轴承力的合力。也就是，可以根据轴承力的分布函数计算出轴承力合力的表达式。轴承力的分布函数的自变量为表示轴承力作用点的物理量(例如，角度)，分布函数中还包括用于表示轴承力的数值大小的参数(例如，h)。在上述分布函数为余弦函数的实施方式中，轴承力是对称分布的，因此轴承力合力的表达式中仅包括参数h。

在步骤s132中，在轴承力的合力等于集中力的情况下，计算分布函数的参数值。也就是，通过使含有参数的轴承力合力的表达式等于集中力f，来建立方程。通过求解方程得到分布函数中的参数值。在上述分布函数为余弦函数的实施方式中，通过求解方程得到以集中力f表示的参数h。

得到参数值之后，就得到了完整的分布函数。此时，已知一自变量(例如，用于表示轴承力的作用点的角度)，根据轴承力的分布函数，就能够得到与该自变量对应的因变量(作用在该作用点上的轴承力的大小)。这样就能够根据所得到的参数值和分布函数来确定轴承力的大小和方向。

在步骤s14中，根据分布函数和参数值计算轴承座101或轴颈102的结构强度。如上所述，已知分布函数和分布函数中的参数值，也就是已知轴承力的大小和方向。根据轴承座101或轴颈102受力的大小和方向来计算所需的结构强度，是本领域技术人员所公知的，因此不再详细描述。

本领域技术人员可以理解的是，在实际应用中，本发明的技术方案能够借助计算机辅助工程来实施。

通过上述技术方案，本发明以更加接近于实际情况的空间分布力代替单一集中力来计算轴承座或轴颈的结构强度，使得计算得到的结构强度更加准确。由于空间分布的面力小于单一的集中力，因此本发明提供的用于滑动轴承的轴承座或轴颈的结构强度计算方法避免了现有技术中对轴承座或轴颈的过设计问题，节约了制作材料。

本发明还提供一种用于滑动轴承的轴承座或轴颈的结构强度计算装置。图7是根据一示例性实施方式提供的用于滑动轴承的轴承座或轴颈的结构强度计算装置的结构框图。如图7所示，所述装置包括集中力计算模块11、分布函数确定模块12、参数值确定模块13、结构强度计算模块14。

集中力计算模块11被配置为计算轴承座101和轴颈102之间相互作用的集中力。

分布函数确定模块12被配置为确定轴承座101和轴颈102之间相互作用的轴承力的分布函数。

参数值确定模块13被配置为根据分布函数和集中力确定分布函数的参数值。

结构强度计算模块14被配置为根据分布函数和参数值计算轴承座101或轴颈102的结构强度。

其中，分布函数确定模块12可以被配置为：根据雷诺方程确定轴承座101和轴颈102之间相互作用的轴承力的分布函数。

所确定的轴承力的分布函数为：轴承力在轴承座101或轴颈102的圆周方向上的120°圆心角所对应的圆弧范围内，呈余弦函数，并且，在轴承座101或轴颈102的轴线方向上的整个宽度范围内，呈余弦函数。

图8是根据一示例性实施方式提供的参数值确定模块13的结构框图。如图8所示，参数值确定模块13包括合力确定单元131和参数值计算单元132。

合力确定单元131被配置为根据分布函数确定轴承力的合力。

参数值计算单元132被配置为在轴承力的合力等于集中力的情况下，计算分布函数的参数值。

关于上述实施例中的装置，其中各个模块执行操作的具体方式已经在有关该方法的实施方式中进行了详细描述，此处将不做详细阐述说明。

以上结合附图详细描述了本发明的优选实施方式，但是，本发明并不限于上述实施方式中的具体细节，在本发明的技术构思范围内，可以对本发明的技术方案进行多种简单变型，这些简单变型均属于本发明的保护范围。

另外需要说明的是，在上述具体实施方式中所描述的各个具体技术特征，在不矛盾的情况下，可以通过任何合适的方式进行组合。为了避免不必要的重复，本发明对各种可能的组合方式不再另行说明。

此外，本发明的各种不同的实施方式之间也可以进行任意组合，只要其不违背本发明的思想，其同样应当视为本发明所公开的内容。