一种含多VSC的多速率电磁暂态分网方法与流程

本发明涉及一种多速率电力系统电磁暂态仿真中的分网并行仿真方法，具体涉及一种含多VSC的多速率电磁暂态分网方法。

背景技术：

多速率仿真技术是精确多速率仿真技术，但是算法的并行化程度不高，系统交互信息量较大，实现实时仿真有难度。而并行接口算法能把两侧网络解耦，提升多速率仿真的并行度，降低系统交互信息，是实现实时仿真的解决方案。目前尚未有适合含多VSC的多速率电磁暂态分网仿真方法。

技术实现要素：

为解决上述现有技术中的不足，本发明的目的是提供一种含多VSC的多速率电磁暂态分网方法，通过网络之间联络的节点作为子网络的边界点，把整个电力系统仿真网络自然的划分为各个子网，通过经验确定不同网络的仿真步长。

本发明的目的是采用下述技术方案实现的：

本发明提供一种含多VSC(VSC voltage source converter，电压源型换流器)的多速率电磁暂态分网方法，其改进之处在于，所述方法包括下述步骤：

步骤1：将网络1划分为子网I和子网II，并通过断面AA相连；设断面AA中有n个节点，m条支路，节点分别为节点a1…an，两两节点之间在断面上无连接；一个支路含有n个节点，

步骤2：建立m个接口系统；

步骤3：建立子网I和子网II包含接口断面的接口系统状态式；

步骤4：对子网I和子网II采用预置的仿真步长离散化；

步骤5：两个耦合系统的动态式转换为两个耦合的离散系统的状态转移式，离散状态转移式明确表示状态变量变化，当k步的X_s和X_f信息确定以后，不用求解整个系统的式，通过递推表达式就能方便地算出k+1时步的信息，进行不同步长子网之间的接口并行计算。

进一步地，所述步骤1中，断面AA中包括节点电压相等的KVL约束和节点电流为0的KCL约束；节点a1…a_n在子网I中的对地电压分别为u_a11…u_an1；节点a1…a_n在子网II中的对 地电压分别为u_a12…u_an2，子网I流出节点a1…a_n的电流分别为i_a11…i_an1；子网II流出节点a1…an的电流分别为i_a12…i_an2，满足的约束条件如下式所示：

其中：u_Aj1、u_Aj2分别为节点a1…an在子网I和子网II中的对地电压；i_Aj1、i_Aj2分别为子网I和子网II流出节点a1…an的电流，j为节点的下标。

进一步地，所述步骤2中，设存在电阻电感和电容典型支路电路的节点关联矩阵为A，A的维数为(n-1)×m，基本回路关联矩阵为B，维数为(m-n+1)×m；n、m分别表示1条支路含有n个节点和m条，根据节点电压相等的KVL约束和节点电流为0的KCL约束，建立m个系统式，表达式如下：

其中：I_s和V_s表示支路元件上的电流和电压相量，维数都是m维；

对于每一个支路元件按照考虑电阻支路、电感支路和电容支路的顺序，重新排列未知相量组V，并设电阻支路、电感支路和电容支路的个数各为x、y、z，如下所示：

V＝[i₁ … i_xv₁ … v_xi₁ … i_zv₁ … v_yi₁ … i_yv₁ … v_z]^T (3)

其中：i₁…i_x分别表示各个电阻支路的电流；i₁…i_y分别表示各个电感支路的电流；i₁…i_z分别表示各个电容支路的电流；v₁…v_x分别表示各个电阻支路的电压；v₁…v_y分别表示各个电感支路的电压；v₁…v_z分别表示各个电容支路的电压；

且知：

其中：Q是2m×2m的变换矩阵；

通过上述知：

其中，A₁₁表示与电阻支路相关的节点关联矩阵，A₁₂表示与电感支路相关的节点关联矩阵，A₁₃表示与电容支路相关的节点关联矩阵；B₁₁表示与电阻支路相关的基本回路关联矩阵， B₁₂表示与电感支路相关的基本回路关联矩阵，B₁₃表示与电容支路相关的基本回路关联矩阵；

由此，由节点电压相等的KVL约束和节点电流为0的KCL约束得到最终关系式：

同时，根据支路的参数关系建立式，如下：

式中，R矩阵表示x个电阻支路的电阻对角矩阵；-I表示一个-1为元素的对角矩阵；L表示y个电感支路的电感对角矩阵，d表示求导算子，C表示z个电容支路的电容对角矩阵；

最终得到一个2m×2m的系数矩阵和未知量相量构成的式，未知量为支路元件电流电压，如下所示：

对式(8)进行处理后，得到只包含状态变量i_y和v_z的状态式：

其中：A_m是一个(m+x)×(m+x)的系数矩阵，表示网络之间的支路元件连接的紧密程度，如下所示：

进一步地，所述步骤3中，子网I是采用小步长仿真的高速子网，仿真步长为h，子网I内部的所有变量的下标使用f表示，子网II是采用大步长仿真的低速子网，仿真步长为m×h，子网II内部的所有变量下标使用s表示；

建立子网I包含接口断面的系统状态式，如下式所示：

式中，表示子网I中的状态变量，包括电感电流，电容电压和控制器中的积分变量；A_f表示子网I中的网络状态矩阵，B_f和D_f均为系数矩阵；U_f是子网I的输入变量，其中U_fint表示子网I内部的注入源，U_fAA‘表示断面接口处的子网注入源，维数为断面的节点数n；Y_fAA’表示断面接口处的输出变量，表示电流；其中B_fint表示B_f矩阵中与U_fint相对应的系数矩阵，D_fint表示D_f矩阵中与U_fint相对应的系数矩阵，B_fAA'表示B_f矩阵中与U_fAA’相对应的系数矩阵；C_f表示子网I的电容对角矩阵；D_fAA'表示D_f矩阵中与U_fAA’相对应的系数矩阵；

建立子网II包含接口断面的系统状态式，如下式所示：

式中：表示子网II中的状态变量，包括电感电流，电容电压和控制器中的积分变量；A_s表示子网II中的网络状态矩阵，B_s和D_s都是系数矩阵；U_s是子网I的输入变量，其中U_sint表示子网I内部的注入源，U_sAA‘表示断面接口处的子网注入源，维数为断面的节点数n；Y_sAA’表示断面接口处的输出变量，表示电流；其中B_sint表示B_s矩阵中与U_sint相对应的系数矩阵，B_sAA’表示B_s矩阵中与U_sAA’相对应的系数矩阵；C_s表示子网II的电容对角矩阵；D_sint表示D_s矩阵中与U_sint相对应的系数矩阵，D_sAA'表示D_s矩阵中与U_sAA’相对应的系数矩阵；

由于断面AA需要满足电路的节点电压相等的KVL约束和节点电流为0的KCL约束定理，接口式满足如下关系：

建立起网络I的状态变量表示的系统式，描述网络内部的动态特性；根据推导过程可知，能准确描述网络I的动态特性，保留系统的所有信息，U_fAA'表示子网1在断面AA处电压，U_sAA'表示子网II在断面AA处电压、Y_fAA'分别表示子网I在断面AA处的等值导纳，Y_sAA'表示子网II在断面AA处的等值导纳。

进一步地，所述步骤4中，对子网I和子网II采用预置的仿真步长进行离散化，分别得到如下表达式：

子网II如下：

上两式中，α和β表示两个系数，采用后退欧拉积分法推导，取α＝0，β＝1；A_f表示子网I中的网络状态矩阵，m表示m条支路、I表示电流向量、h表示步长、k分别表示当前计算时步，k+1表示下一计算时步；B_fint表示B_f矩阵中与U_fint相对应的系数矩阵，B_fAA'表示B_f矩阵中与U_fAA’相对应的系数矩阵；U_f是子网I的输入变量，其中U_fint表示子网I内部的注入源，U_fAA‘表示断面接口处的子网注入源，维数为断面的节点数n；B_sint表示B_s矩阵中与U_sint想对应的系数矩阵，B_sAA’表示B_s矩阵中与U_sAA’相对应的系数矩阵；D_sint表示D_s矩阵中与U_sint相对应的系数矩阵，D_sAA'表示D_s矩阵中与U_sAA’相对应的系数矩阵；D_fint表示D_f矩阵中与U_fint相对应的系数矩阵，D_fAA'表示D_f矩阵中与U_fAA’相对应的系数矩阵；

简化式(14)和(15)：

多速率仿真算法需要保证断面AA的电路约束式(14)、式(15)不变，网络1系统的状态转移式如下所示：

其中Δ＝(B_sAA'C_s+D_fAA'+D_sAA'+B_fAA'C_f)^-1，U_sint和U_fint是子网内部的注入电源的取值。

与最接近的现有技术相比，本发明提供的技术方案具有的优异效果是：

本发明提供一种含多VSC的多速率电磁暂态分网仿真方法，通过网络之间联络的节点作为子网络的边界点，把整个电力系统仿真网络自然的划分为各个子网，根据精度需要确定不同网络的仿真步长。本发明提供的方法在网络划分时不需要解耦元件，网络划分简单清楚，通用性强，分网速度快。可以并行仿真不同速率、不同步长的含VSC精确模型的电磁暂态子网进行实时、超实时仿真。

附图说明

图1是本发明提供的多速率仿真系统的基本结构示意图；

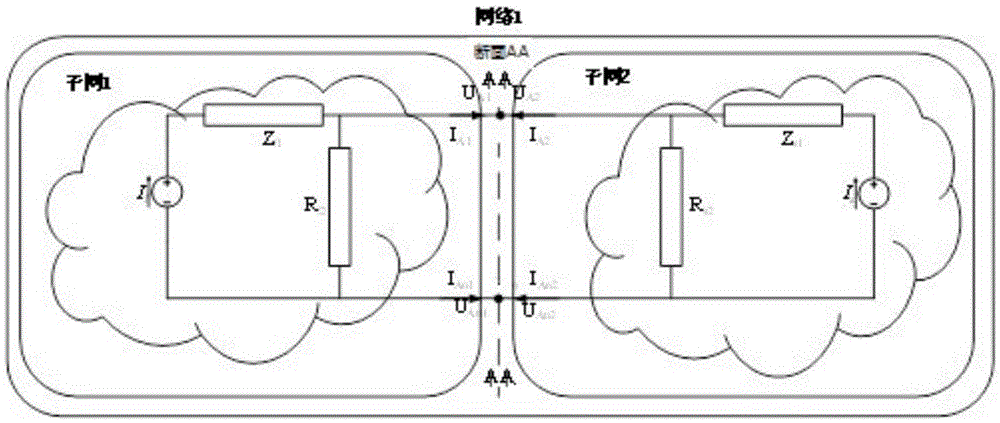
图2是本发明提供的基于本发明的网络分割示意图；

图3是本发明提供的支路典型电路模型图。

具体实施方式

下面结合附图对本发明的具体实施方式作进一步的详细说明。

以下描述和附图充分地示出本发明的具体实施方案，以使本领域的技术人员能够实践它们。其他实施方案可以包括结构的、逻辑的、电气的、过程的以及其他的改变。实施例仅代 表可能的变化。除非明确要求，否则单独的组件和功能是可选的，并且操作的顺序可以变化。一些实施方案的部分和特征可以被包括在或替换其他实施方案的部分和特征。本发明的实施方案的范围包括权利要求书的整个范围，以及权利要求书的所有可获得的等同物。在本文中，本发明的这些实施方案可以被单独地或总地用术语“发明”来表示，这仅仅是为了方便，并且如果事实上公开了超过一个的发明，不是要自动地限制该应用的范围为任何单个发明或发明构思。

多速率仿真系统采用空间网络分割，包含了慢速系统，快速系统和多速率仿真接口。具体的多速率系统结构图如图1所示。

上图中，Main Circuit表示电力系统仿真中的主网架，包括了大量的发电机、变压器、负荷、传输线、LCC的电力电子电路和一些等值电路，网络规模庞大结构复杂，同时也没有高速IGBT的动作，系统的时间常数较大，系统响应较慢是慢速系统，采用大步长(例如，50μs)，此部分采用常规的电磁暂态仿真技术。

椭圆A，B，C，D，E表示一些快速子网络，其包含VSC和一些与其紧密耦合的元件，如相电抗器、换流变压器和暂态滤波器、直流侧电容器和风机或太阳能发电设备等。快速子网需要对触发脉冲做到精确响应，应使用很小的仿真步长进行模拟(例如，1-3μs)。子网通过多速率仿真接口(节点或者传输线)与主Main Circuit相连，子网与子网之间相互没有电气联系。不同的多速率仿真技术存在着准确性、稳定性和计算效率之间的差别。

本发明是通过网络之间联络的节点作为子网络的边界点，把整个电力系统仿真网络自然的划分为各个子网，通过经验确定不同网络的仿真步长。本发明在网络划分时不需要解耦元件，网络划分简单清楚，通用性强。

本发明提供一种含多VSC的多速率电磁暂态分网仿真方法，包括下述步骤：

步骤1：将网络1划分为子网I和子网II，并通过断面AA相连；设断面AA中有n个节点，分别为节点a1…an，两两节点之间在断面上无连接；

为了便于理论推导和阐述，如图2所示假设网络1划分为子网I和子网II，通过断面AA相连。设断面AA中存在n个节点，为节点a1…an，节点与节点之间在断面上没有连接。

图2中云形图案中的网络拓扑不确定，电源加电阻的模型只是一个示例，并不是真正的子网内元件。子网I和子网II拥有任意的网络拓扑，内部元件可按照用户需要进行搭建。考虑仿真效率，电磁暂态仿真对于非线性环节的处理采用了分段线性化方法和伴随法，子网I和子网II内部的元件不再局限于线性元件，仿真算法具有通用性。

不同网络之间断面的物理约束表示了网络之间的耦合约束，断面AA中包括了节点电压 相等的KVL约束和节点电流为0的KCL约束。例如，假设节点a1…an在子网I,2中的对地电压分别为u_a11…u_an1和u_a12…u_an2，流出节点的电流分别为i_a11…i_an1和i_a12…i_an2，满足的约束条件如下式所示：

电路中存在电阻电感和电容典型支路，支路的典型图可表示为图3：

图3中支路ij上，R(L，C)表示电阻元件(电容、电感元件)，I_s表示电流源，V_s表示电压源，i和j表示支路两端的节点，i_ij表示通过支路元件的电流，u_ij表示支路中元件的电压,支路的典型表达式即为下述三个式子：

u_ij＝Ri_ij

取任意电路，设电路的节点关联矩阵为A，A的维数为(n-1)×m，基本回路关联矩阵为B，维数为(m-n+1)×m。

步骤2：建立m个接口系统；

根据KVL和KCL，建立起m个系统式：

其中i和v表示支路元件上的电流和电压相量，维数都是m维。

对于每一个支路元件可以按照考虑电阻支路，再电感支路，电容支路的顺序，重新排列未知相量组V，并假设电阻支路、电感支路、电容支路的个数各为x、y、z，如下所示：

V＝[i₁ … i_xv₁ … v_xi₁ … i_zv₁ … v_yi₁ … i_yv₁ … v_z]^T (3)

且易知：

Q是2m×2m的变换矩阵。

通过变化可以知道：

其中，A₁₁表示与电阻支路相关的节点关联矩阵，A₁₂表示与电感支路相关的节点关联矩阵，A₁₃表示与电容支路相关的节点关联矩阵；B₁₁表示与电阻支路相关的基本回路关联矩阵，B₁₂表示与电感支路相关的基本回路关联矩阵，B₁₃表示与电容支路相关的基本回路关联矩阵。

由此，由KVL，KCL得到最终关系式：

同时，根据支路的参数关系可以建立另一些式子，如下所示：

上式中，R矩阵表示x个电阻支路的电阻对角矩阵；-I表示一个-1为元素的对角矩阵；L表示y个电感支路的电感对角矩阵，d表示一个求导算子，C表示z个电容支路的电容对角矩阵。

步骤3：建立子网I和子网II包含接口断面的接口系统状态式；

综合上述，可以得到一个2m×2m的系数矩阵和未知量(支路元件电流电压)相量构成的式。

对该式(11)进行处理后，得到只包含状态变量i_y和v_z的状态式：

其中A_m是一个(m+x)×(m+x)的系数矩阵，表示网络之间的支路元件连接的紧密程度，如所示：

对于上述推导中没有考虑的复杂多端口网络支路也可以较容易的定义为多输入多输出的系统结合到电路状态空间表示中来。

按照本发明分网，图2的网络1可以通过电压源分解为两个子网络：子网I和子网II，子网之间符合电压相等的约束，还符合电流为0的约束。

本发明定义子网I是采用小步长仿真的高速子网，仿真步长为h，子网I内部的所有变量的下标使用f(fast)表示，而子网II是采用大步长仿真的低速子网，仿真步长为m×h，子网II内部的所有变量下标使用s(slow)表示。

建立子网I包含接口断面的系统状态式，如所示：

上式中，X_f表示子网I中的状态变量，包括电感电流，电容电压和控制器中的积分变量。A_f表示子网I中的网络状态矩阵，求法参考式(2)～(6)，B_f和D_f都是系数矩阵。U_f是子网I的输入变量，其中U_fint表示子网I内部的注入源，U_fAA‘表示断面接口处的子网注入源，维数为断面的节点数n。Y_fAA’表示断面接口处的输出变量，表示电流。其中B_fint表示B_f矩阵中与U_fint相对应的系数矩阵，B_fAA’表示B_f矩阵中与U_fAA’相对应的系数矩阵。

建立子网II包含接口断面的系统状态式，如式(12)所示：

此式中的系数的含义与式(1)相同。为了易于表述系统，上式中X_s表示子网II中的状态变量，包括电感电流，电容电压和控制器中的积分变量。A_s表示子网II中的网络状态矩阵，B_s和D_s都是系数矩阵。U_s是子网I的输入变量，其中U_sint表示子网I内部的注入源，U_sAA‘表示断面接口处的子网注入源，维数为断面的节点数n。Y_sAA’表示断面接口处的输出变量，表示电流。其中B_sint表示B_s矩阵中与U_sint想对应的系数矩阵，B_sAA’表示B_s矩阵中与U_sAA’相对应的系数矩阵。D_sint表示D_s矩阵中与U_sint相对应的系数矩阵，D_sAA'表示D_s矩阵中与U_sAA’相对应 的系数矩阵；D_fint表示D_f矩阵中与U_fint相对应的系数矩阵，D_fAA'表示D_f矩阵中与U_fAA’相对应的系数矩阵；

由于断面AA需要满足电路的KVL，KCL定理，由此可知接口式满足如下关系：

综合式(8)到(12)可以建立起网络1的状态变量表示的系统式(13)，描述网络内部的动态特性。根据推导过程可知，此式没有任何简化，能准确描述网络1的动态特性，保留了系统的所有信息。

步骤4：对子网I和子网II采用预置的仿真步长(子网I是采用小步长仿真的高速子网，仿真步长为h(h一般为1-10us)，子网I内部的所有变量的下标使用f(fast)表示，而子网II是采用大步长仿真的低速子网，仿真步长为m×h，(m×h一般为30-100us))离散化(离散化的目的是对大的子网方程进行分解成每个小的步长计算公式，来进行计算，这是递推计算的一种计算基本形式)。

对两个子网采用预置的仿真步长进行离散化，可以得到如下表达式：

子网I如下：

子网II如下：

上两式中，α和β表示两个系数，这个系数由不同的积分方法决定，当积分方法不同时，离散化的结果也可能不同。为了简化分析，在本发明后续推导过程中采用后退欧拉积分法(α＝0，β＝1)。

为了式描述的简化，对式(14)和(15)中的一些符号做如下简化：

多速率仿真算法需要保证断面AA的电路约束式(14)、式(15)不变，再结合式(16)、(17)，可以推导出网络1系统的状态转移式如下所示：

其中Δ＝(B_sAA'C_s+D_fAA'+D_sAA'+B_fAA'C_f)^-1

上式中，U_sint和U_fint是子网内部的注入电源的取值。由于子网内部的注入电源完全由电源本身的函数表达式确定，不由电路状态决定，不需要求解电网络式就可以得到。

步骤5：至此，两个耦合系统的动态式可以转换为两个耦合的离散系统的状态转移式，离散状态转移式可以明确表示状态变量变化，当k步的X_s和X_f信息确定以后，不用求解整个系统的动态式，通过递推表达式就能方便地算出k+1时步的信息，进行不同步长子网之间的接口并行计算。

以上实施例仅用以说明本发明的技术方案而非对其限制，尽管参照上述实施例对本发明进行了详细的说明，所属领域的普通技术人员依然可以对本发明的具体实施方式进行修改或者等同替换，这些未脱离本发明精神和范围的任何修改或者等同替换，均在申请待批的本发明的权利要求保护范围之内。