一种模拟桥墩周期受力的数值方法与流程

本发明涉及计算流体力学应用领域中的一种数值方法，具体是一种模拟桥墩周期受力的数值方法。

背景技术：

当河流经过大型桥墩物时，因为桥墩的迎风面和背风面的压力差的存在，在桥墩的后方会产生水流的漩涡。漩涡随着流水向下方继续流动，形成一系列脱落涡。这一系列脱落涡的流动也被称为卡门涡街，是一个充满了旋涡的旋流场，河流水流流场可以被视为是一个不可压缩流动。实际上，脱落涡会对桥墩周期地产生诱导作用力，严重的会使建筑物晃动，如果涡脱落的周期和桥墩建筑的自激频率相接近，建筑物的晃动会被放大，甚至发生毁坏。

对于桥墩周期受力有多种研究手段。其中，计算机的数值模拟技术有着重要地位，是计算流体力学在该领域的一个扩展应用。计算流体力学综合了流体力学、应用数学、计算机科学，是一门应用性极强的学科。流体力学问题的数值模拟以其低成本、直观性强的优势，在流体流动的机理探索、工业产品设计等各个相关领域占据重要地位。桥墩后方脱落涡的数值模拟面临的最大的问题即是如何提高数值模拟的精度、降低误差，忠实地表现桥墩后方脱落涡流动的特性。

影响流体力学问题的数值模拟的精度的重要因素之一是：当使用数值方法求解流体控制方程，即欧拉(euler)方程或者纳维尔-斯托克斯(navier-stokes)方程时，会产生数值耗散(numericaldiffusion)，造成数值解的误差。例如数值方法中对控制方程的对流项的空间离散方法(如中心差分、迎风差分)、时间离散方法(如显示时间积分、隐式时间积分)、湍流模型(如双方程模型、大涡模拟)的使用，以及计算网格正交性都会产生不同程度的数值耗散。此外，数值模拟中还经常要使用一种人工数值耗散(artificialdiffusion)技术，其目的是通过适当降低计算精度而获得稳定的数值解。

数值耗散对流场的数值模拟结果的最明显的影响体现在对流动变量的不连续界面(discontinuity)的捕捉。流场中一种强不连续的界面的捕捉，例如激波(shock)的捕捉，即是依靠加入适量的人工耗散项，以避免数值解在流动变量梯度变化较大的地方出现数值振荡现象。数值耗散可以理解为是流场中的一种能量损失，这种能量损失在某种程度上使得数值模拟结果不能忠实的体现流体的流动特性，降低了计算精度。先进的数值方法应该是在保证获得稳定性的数值解的前提下，将数值耗散减至最小。激波是强间断界面，对其捕捉必须加入一定的人工数值耗散。因为激波前后存在熵增，即能量的损失，所以，通过加入适当的人工数值耗散捕捉激波具有合理的物理意义。但是，诸如桥墩后方脱落涡一类的流动，存在着流场中另一类流动不连续现象，即接触不连续(contactdiscontinuity)。旋涡的产生自然和其周围的流体产生一个不连续面。这个接触不连续面相对激波而言是弱不连续，跨过不连续界面，压力和法向速度是连续的。数值模拟中对于这种接触不连续的捕捉更加困难，因为数值方法中的数值耗散即使很小也会使弱不连续界面变得模糊，降低数值解对流场的预测精度，这也是诸如桥墩后方脱落涡一类的旋流场的数值模拟技术成为cfd领域的重大挑战的原因。

为了提高桥墩后方脱落涡流场的数值模拟的精度，一种方法是加密计算网格，在更加细小的空间尺度内求解流体控制方程。加密计算网格首先会使计算量加大，增加计算成本。此外，数值计算的误差随着计算网格的增加会不断积累，在一定程度上造成相反的效果。另一种方法是在流场中采用物理模型来增加流场中描述旋流流动的变量—涡量(vorticity)的强度。例如在流场中加入点涡模型，可以人为地增加涡量；或者在流场局部直接求解涡量方程，以减小涡量的输运过程中的耗散。但是，这些方法在应用上仍受到一定限制。点涡模型是在预先明确旋涡发生位置的前提下才能使用，仅适合一些简单的流动现象。除了二维不可压缩正压流场，涡量方程比与欲求解的euler、navier-stokes方程更为复杂。

二十世纪初期，美国科学家johnsteinhoff提出了一种提高不可压缩旋流场的求解精度的数值方法，涡量限制法(vorticityconfinement)。该方法的原理是依靠在流场中加入限定的涡量以抵消数值耗散来模拟旋流场的流动状态。具体表现形式是在流体控制方程的动量方程中的源项位置，加入一个涡量形式的体积力项，从数值耗散中将涡量减去，克服数值耗散造成的旋涡场的接触不连续界面的模糊，从而更精确地捕捉旋涡结构，实现提高旋涡场的计算精度的目的。原始的涡量限制法是公知的，这里不再叙述。尽管该方法在捕捉不可压缩流场中的接触不连续的方面已经取得了明显的改进效果，但存在以下缺陷：

1.对加入的涡量调整完全靠常系数；

2.加入的涡量的空间离散精度是被限定的，无法进一步提高；

3.源项对动量方程的数值解的收敛的稳定性影响是不确定的。

为了更加精确地模拟桥墩后方脱落涡流动—不可压缩无粘流的旋涡运动，需要进一步改进对于流场中接触不连续的捕捉机制。一种途径是根据不可压缩流的特点，改进在流场中通过加入涡量来抵消数值耗散的内在工作机理，通过保持涡量的精度，更精确地用模拟流场中的旋涡运动，形成一种新的，针对桥墩后方的涡脱落长生的周期受力的数值模拟技术。该技术可以使涡量的空间离散具有高阶精度的格式，同时该可以利用源项增进收敛进程的稳定性。

技术实现要素：

本发明涉及计算流体力学的应用领域中一种模拟桥墩周期受力(不可压缩无粘旋流流动)的数值方法，具体是根据不可压缩流的特点，在流场中通过加入两种不同形式的涡量力来抵消数值耗散的数值方法。该方法可以使加入的涡量的空间离散具有高阶精度的格式，同时还可以利用源项增进数值解的收敛进程的稳定性。通过保持涡量的精度，更精确地用模拟流场中的旋涡运动，是一种新的不可压缩流的旋涡运动的数值模拟技术。

首先写出不可压缩、无粘流流动的控制方程，包括连续方程和动量方程，分别为

式中，v是速度矢量，包含直角坐标系下的三维i，j，k分量u，v，w；ρ、p、t分别是密度、压力和时间。式中算子表示为符号·代表内积计算。动量方程(2)的右边是体积力项形式的源项按照涡量限制法中的定义

式中，代表涡量，在直角坐标系下有按照涡量的定义，

式中符号×代表叉乘运算，代表涡量梯度变化的方向，即

其中，φ是涡量的模；是涡量的模的梯度的模，即

动量方程(2)中的源项需要公式(3)中的乘以一个比例因子ε，则

其物理意义是指向涡量中心的力。原始的涡量限制法中给出ε为常数，为0.01-0.05，其作用是用来调整涡量限制的大小。该方法形式简单，不需要加密计算网格，在不可压缩旋流场的数值模拟中得到广泛应用。对该方法在随后的改进主要集中在参数ε的表达。

如公式(2)表示的，涡量限制法中在不可压缩流动的动量方程的等号右边加入了一个体积力项，它代表涡量在其变化梯度相反的方向的受力，如公式(7)所示。实际上，如果将公式(4)带入公式示(7)并运用算子的运算规律可得

在上式中再次运用算子的运算规律可得

式中是拉普拉斯算子，定义为又根据公式(1)不可压缩流的连续方程，将公式(9)代入公式(8)，可得

对于不可压缩流，公式(10)与公式(7)完全等价。现将公式(10)中的重新写成如下形式，即

其中，

因为是螺旋度的定以，所以被称作涡量在变化梯度方向的螺旋力；

因为拉普拉斯算子的耗散特性，被称作在涡量在变化梯度方向的粘性耗散力。

至此公式(2)中以动量方程的源项形式表示的涡量在其变化梯度相反的方向的受力(涡量限制)限制被分解为两部分，形成两种力的形式。其中涡量在变化梯度方向的螺旋力与涡量的变化方向和涡量大小有关；而涡量在变化梯度方向的粘性耗散力仅与涡量的变化梯度方向有关。图2给出两种形式的力的形成原理和关系图。图中表明，由涡量和涡量梯度变化的方向向量构成平面1，被称作涡量作用平面。原始的涡量限制与该平面垂直，并与它的两个分量，涡量在变化梯度方向的螺旋力和涡量变化梯度方向的粘性耗散力共同构成平面2，被称作涡量限制平面。平面1垂直与平面2。和的夹角被称作螺旋角，该夹角的余弦即为涡量限制被分解后形成的两种形式的力，和将在数值方法中起到不同的作用。

公式(12)和(13)中是用了两个参数：ε1和ε2，分别作为不同的两个力的放大系数。如果ε1和ε2相等，且等于公式(7)中的ε，则成为同向涡量限制(isotropicvorticityconfinement)，其效果等同于公式(7)表示的原始的涡量限制；而ε1和ε2不相等时，成为异向涡量限制(anisotropicvorticityconfinement)。而不可压缩旋流场的数值模拟精度的提高可以通过异性涡量限制获得。

作为源项形式的体积力对偏微分方程(2)的数值解的收敛过程有重要影响。其作用体现在加入源项后，方程(2)有可能变成具有刚性的(stiff)的性质，致使一类依靠显式时间迭代获得数值解的收敛性降低，同时也降低数值解的稳定性。因而，此类方程的求解为了保证时间精度，必须采用较小的时间步长，结果造成计算速度变慢。衡量方程的刚性的指标是源项的雅各比矩阵的特征值。如果雅各比矩阵的最大特征值和最小特征值的实部的比例小，则说明偏微分方程的刚性小，数值解容易收敛，而且稳定性强。

考虑两种情况：第一，源项分别为即原始的涡量限制法中的体积力，源项的雅各比矩阵为特征值为i等于2或3；第二，源项为即涡量变化梯度方向的粘性耗散力，源项的雅各比矩阵为特征值为在两种形式的体积力的情况下，源项的雅各比矩阵分别表示为

按照雅各比矩阵的特征值的求解方法，求解下式

和其中i是单位矩阵，即可获得两种源项的特征值，而且有

上式中re表示取实部运算。表明了以为源项时，偏微分方程的刚性比以为源项时小。因而，在使用一类显式时间积分方法求解不可压缩流的动量方程(2)时会增强收敛性和数值稳定性。所以，利用这个特性，可以将(涡量在变化梯度方向的螺旋力)从等号右边移动到等号左边，等号右边的源项仅保留(涡量变化梯度方向的粘性耗散力)。

如公式(12)所示，涡量在变化梯度方向的螺旋力与涡量的变化方向和涡量大小有关，数值解中需要高精度的空间离散，以提高模拟精度。源项中的被移动等号左边后，可以利用高斯定理，将控制体单元内的体积力形式转变为表面通量的积分形式。有限体积法(finitevolumemethod)中，某一控制体单元，即某一计算网格的体积为ω，而其表面积为面积元为ds。根据高斯定理，可将体积积分变换为面积积分，则涡量在变化梯度方向的螺旋力从体积积分变为面积积分的过程可表示为

其中计算网格边界的单位向量。于是，在计算网格边界上产生了一个由于涡量在变化梯度方向的螺旋力产生的向量，被称作涡量的螺旋力向量

在数值解的求解过程中，可以对该向量在计算网格边界上进行高阶精度的空间离散。由于该向量与涡量的变化方向和涡量大小有关，为进一步提高了旋涡流场的空间模拟精度提供了可能性。例如可以同过流动变量的高阶插值获得计算网格界面上用来计算向量的值。

此外，如果适当增大ε1、减小ε2，意味着增大涡量在变化梯度方向的螺旋力、降低涡量变化梯度方向的粘性耗散力，即采用异向涡量限制，利用调节这两个力的内部关系的机制，可以进一步调整旋涡运动中的接触不连续界面的捕捉效果。

总之，本发明提出的提高不可压缩旋流场的数值模拟精度的数值方法包括四个技术元素，分别为：

1.将涡量限制法中的源项分解称为两个力，涡量在变化梯度方向的螺旋力和涡量变化梯度方向的粘性耗散力，并将涡量在变化梯度方向的螺旋力移动到不可压缩流的动量方程的等号左变；

2.通过高斯定理将计算网格内涡量在变化梯度方向的螺旋力转化为计算网格边界上的上的力，进行高精度的空间离散，按照通量进行计算；

3.源项保留涡量变化梯度方向的粘性耗散力用来提高数值解的收敛性和稳定性；

4.涡量在变化梯度方向的螺旋力和涡量变化梯度方向的粘性耗散力采用不同的放大系数，即采用异向的涡量限制。

本发明提出的提高桥墩后方脱落涡不可压缩旋流场的数值模拟精度的数值方法是根据不可压缩流的特点，通过加入两种不同形式的力来改进在流场中抵消数值耗散的内在工作机制，使计算网格内的涡量在变化梯度方向的螺旋力转化为计算网格边界上的上的力，可以使其空间离散具有高阶精度的格式；同时源项保留涡量变化梯度方向的粘性耗散力，用来提高数值解的收敛性和稳定性。这两个力采用不同的放大系数，可以进一步保持涡量的精度，更精确地模拟桥墩后方脱落涡流场中的旋涡运动。

附图说明

图1桥墩后方的流动模式。图中，4桥墩、5周期性涡脱落、6来流方向。

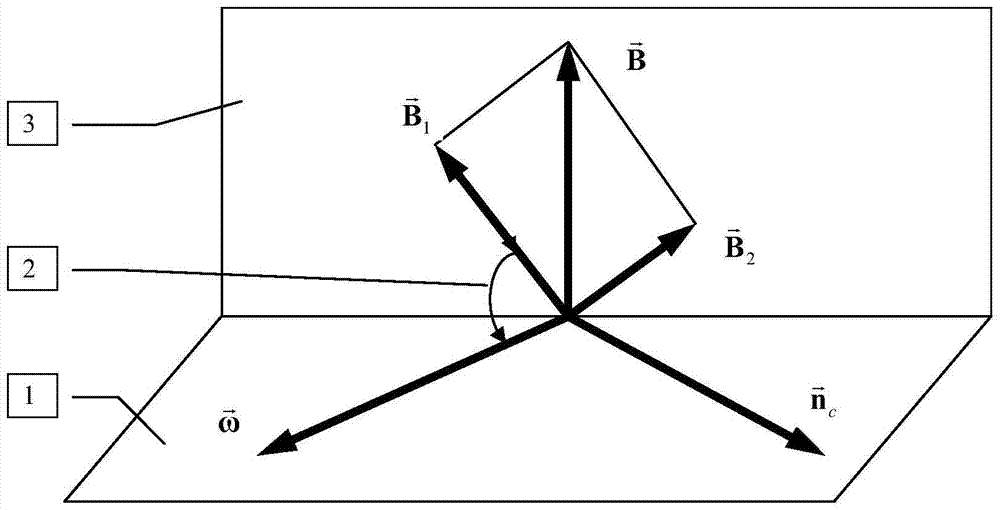
图2涡量在变化梯度方向的螺旋力和涡量变化梯度方向的粘性耗散力形成原理和关系图图中，1涡量作用平面、2螺旋角、3涡量限制平面。

图3模拟桥墩周期受理的流程图

具体实施方式

以下以一个具体实施方案进一步说明本发明提出的模拟桥墩周期手里的数值方法。这种数值模拟技术可以用fortran90计算机高级程序语言实现，并通过计算机运行来模拟三维流动的周期性涡脱落流场。

具体实施方案中，桥墩其周围的流场是以旋涡运动为主的流场。计算网格采用多块结构化适体六面体网格，桥墩周围采用o-型网格，围绕桥墩剖面方向192个网格；法线方向68个网格；翼展方向96个网格。数值模拟的空间离散采用有限体积法(finitevolumemethod)，每个计算网格成为控制单元，流动变量在控制单元的中心。

数值模拟的条件是：

来流速度：57m/s；

流体密度：1000kg/m^3；

不可压缩无粘流的动量方程，即方程(2)中不计粘性项。本发明中要求加上在计算网格边界上产生了一个由于涡量在变化梯度方向的螺旋力产生的向量意味着在动量方程左边的对流项后面加上这个向量，在等号右边，即源项的位置加上涡量变化梯度方向的粘性耗散力按照守恒定律，将动量方程(2)简化写成适合河流流动模拟的粘性不可压缩浅水方程的形式，并写出积分形式，

其中，守恒变量对流项向量和涡量的螺旋力向量(见公式(19))分别为

上式中，密度ρ为一固定值(不可压缩流)；v代表速度不变量，是网格边界的外法线向量与速度向量的点乘，即

可以将对流项向量写成展开形式，

对流项经压力分离后，可以写成不计压力的对流项向量和压力向量之和，显然有，

其中，

进一步可以写出本发明提出的涡量在变化梯度方向的螺旋力向量和源项形式的涡量变化梯度方向的粘性耗散力的具体形式分别为，

其中，涡量的模φ和涡量的模的梯度的模由公式(5)和(6)给出。公式(28)和(29)中涉及的一阶导数和二阶导数项均可利用格林公式求取或者直接按照泰勒展开求取，其过程是公知的，不再叙述。

图3给出了本实施例模拟桥墩后方脱落涡的流程图。公式(20)至(29)体现了这个流程中直至生成模拟桥墩后方脱落涡的不可压缩流控制方程，即包含涡量在变化梯度方向的螺旋力向量和涡量变化梯度方向的粘性耗散力的不可压缩无粘流的动量方程。下面的步骤是求解这个方程。

以下是本实施例在同位网格(collocatedgrid)中运用标准的基于压力的方法(pressure-basedmethod)求解包含涡量在变化梯度方向的螺旋力向量和涡量变化梯度方向的粘性耗散力的不可压缩流控制方程的过程。

首先将公式(20)写成离散形式，

其中，ωi,j,k代表空间任一离散控制体体积；△t代表积分时间步长；代表流场更新后速度；△sm代表控制体任一表面面积；nf代表控制体表面个数，三维情况下为6。重新整理右手项，有

而使用一个假设的初始速度计算一个不计压力项的右手项即

显然有，

不计压力项时候，可以从公式(31)获得这个初始速度场

其中需要在计算网格边界m上的不计压力的对流项向量涡量在变化梯度方向的螺旋力向量以及在计算网格内的涡量变化梯度方向的粘性耗散力再带入公式(33)以获得不计压力的右手项

在按照公式(28)计算网格边界m处的涡量在变化梯度方向的螺旋力向量的时候，对于其中的一阶导数项采用高精度离散方法，例如在i-方向的三阶空间离散表示为，

网格中心点的初始速度在计算网格边界上利用公知的muscl方法进行二阶精度插值，可获得在网格边界m上的速度因而，根据公式(35)不计压力项的情况下，在边界m处的速度表示为

其中，是包含网格边界m的辅助网格的体积。在边界m处，考虑压力项的速度为

其中，是公式(32)在网格边界m处的值，仍然用muscl方法进行二阶插值获得。整理公式(37)和(38)，有

考虑压力项的速度应该满足不可压缩流的连续方程(1)，即将连续方程(1)写成离散形式，

将公式(39)带入(40)，有

求解方程(41)，即可获得t+△t时刻，流场的计算网格边界m处的速度和压力值pm，这两个值可以通过集合平均处理，转化为计算网格中心处的值。

以上是本发明提出的一种模拟桥墩周期性受力流动的数值方法的论述。