一种扩散加权成像方法与流程

【技术领域】

本发明涉及磁共振成像技术领域，尤其涉及一种体素内非相干运动扩散加权成像方法。

背景技术：

扩散加权成像(diffusionweightedimaging，dwi)属于功能影像学的范畴，是目前唯一在体测量组织内水分子扩散运动的成像方法，其成像的原理是利用水分子的布朗运动，无需注射对比剂即可其反应人体组织的微观结构以及细胞内外水分子的转移与跨膜运动、温度等的变化。通过dwi图像信号高低的定性比较及表观扩散系数(apparentdiffusioncoefficient，adc)的定量测量对组织结构及功能变化进行评估，可用于显示疾病的敏感性以及诊断和鉴别诊断等方面。

在传统扩散理论中，水分子在一定时间内从某一部位扩散到另一部位的位移运动呈高斯分布，dwi影响信号随着b值的增加呈单指数函数衰减。然而，由于细胞膜、细胞内外间隔等扩散障碍物的影响使生物组织中水分子的扩散比自由水的扩散复杂，组织中水分子的位移偏离高斯分布。另外，基于多b值dwi研究发现，dwi信号随b值增大并不遵循单指数递减规律。dwi影像上信号衰减同时包括真性水分子扩散和毛细血管网中随机血流微循环灌注，后者使扩散影像上出现假扩散信号，导致adc值反应的信息有限，这种现象即为体素内非相干运动(intravoxelincoherentmotionimaging，ivim)。基于ivim双指数模型的dwi是采用多个b值的扫描成像，可以分离出组织的真实扩散 信息和微循环灌注信息。lebihan等^[1]首次将ivim-dwi应用于临床，主要用于将水分子扩散与毛细血管微循环灌注区分开，不仅对神经系统，而且对其他各部位的多种生理和病例机制都能提供定量指标，成为广泛关注的新兴成像热点。

但是ivim参数成像的一个常见问题是图像的较弱信噪比导致的参数估计的可靠性较差。传统方法多采用高斯方法去噪，但是dwi中噪声主要成像rician(莱斯)分布，因此基于高斯噪声的去噪方法容易产生误差。此外，还存在各种改进ivim成像参数可靠性的方法，如加权均值滤波、线性最小均方误差、非局部均值滤波等。然而这些方法有些需要额外的数据采样平均，还有些需要复杂的计算方法，在实际应用中都有一定的局限性。基于此，有必要对现有ivim-dwi成像方法进行改进，在去除噪声的同时改善ivim成像参数的可靠性。

[1]、lebihand,bretone,lallemandd,etal.separationofdiffusionandperfusioninintravoxelincoherentmotionmrimaging[j].radiology,1988,168(2):497-505.

技术实现要素：

本发明所要解决的技术问题是提出一种可提高体素内非相干运动扩散加权成像中ivim参数估计可靠性的方法。

本发明解决上述技术问题所采用的技术方案为一种扩散加权成像方法，包括如下步骤：

利用磁共振扫描仪采集受检者多个b值dwi图像；

采用基于svd-pca的方法对所述dwi图像进行降噪处理，获取降噪处 理后的dwi图像；

对所述降噪处理后的dwi图像进行非线性拟合，获得体素内非相干运动的参数估计，所述参数包括真性扩散系数、假性扩散系数和灌注分数。

进一步地，所述采用基于svd-pca的方法对所述dwi图像进行降噪处理的具体过程为：

将所述dwi图像分解成若干个图像块，相邻图像块之间存在重叠部分；

将所述图像块展成矢量组成矢量合成矩阵；

对所述矢量合成矩阵进行奇异值分解，获取所述矢量合成矩阵中各基矢量的分量值；

根据设定阈值对所述分量值进行过滤处理获取去噪后的合成矩阵，并对去噪后的合成矩阵作svd反变换获取去噪后的dwi图像。

进一步地，还包括对相邻图像块之间重叠部分所展成的矢量作均值处理。

进一步地，对所有b值dwi图像的每个b值dwi图像分别进行降噪处理，且每个b值dwi图像都有对应的矢量合成矩阵。

进一步地，对所有b值dwi图像中的至少两个同时进行降噪处理，且同一b值dwi图像的不同图像块展成的矢量对应矢量合成矩阵的不同行，不同b值dwi图像中相同位置的图像块展成的矢量对应矢量合成矩阵的同一行。

进一步地，所述根据设定阈值对所述分量值进行过滤处理的具体过程为：对小于设定阈值的分量值作置零处理，并保留大于或等于设定阈值的分量值。

进一步地，所述设定阈值通过如下方式获得：

分别采用不同阈值对各分量值进行过滤处理，得到不同阈值对应的合成矩阵；

对不同阈值对应的合成矩阵作svd反变换获得不同阈值所对应的dwi重 建图像；

计算不同阈值所对应的dwi重建图像间的均方差并获取均方差曲线，所述设定阈值为所述均方差曲线上峰值位置后端所对应的阈值。

进一步地，采用levenberg-marquardt对所述降噪处理后的dwi图像进行非线性拟合获取计算参数值，并根据所述计算参数值获取参数估计值。

进一步地，所述参数估计的值为所述计算参数值的平方。

进一步地，根据高b值dwi图像估计所述真性扩散系数，根据全部b值dwi图像估计所述假性扩散系数和灌注分数。

与现有技术相比，本发明的优点在于：在对多个b值dwi图像进行非线性拟合前，采用基于svd-pca的方法将多个b值dwi图像展成矢量合成矩阵，通过对矢量合成矩阵的奇异值进行过滤处理可有效去除dwi图像的噪声成分，提高信噪比，进而提高体素内非相干运动参数估计的可靠性；在采用levenberg-marquardt对所述降噪处理后的dwi图像进行非线性拟合的过程中，将估计参数采用变量平方替换，保证所有参数估计的非负性，参数估计可靠性进一步提高。

【附图说明】

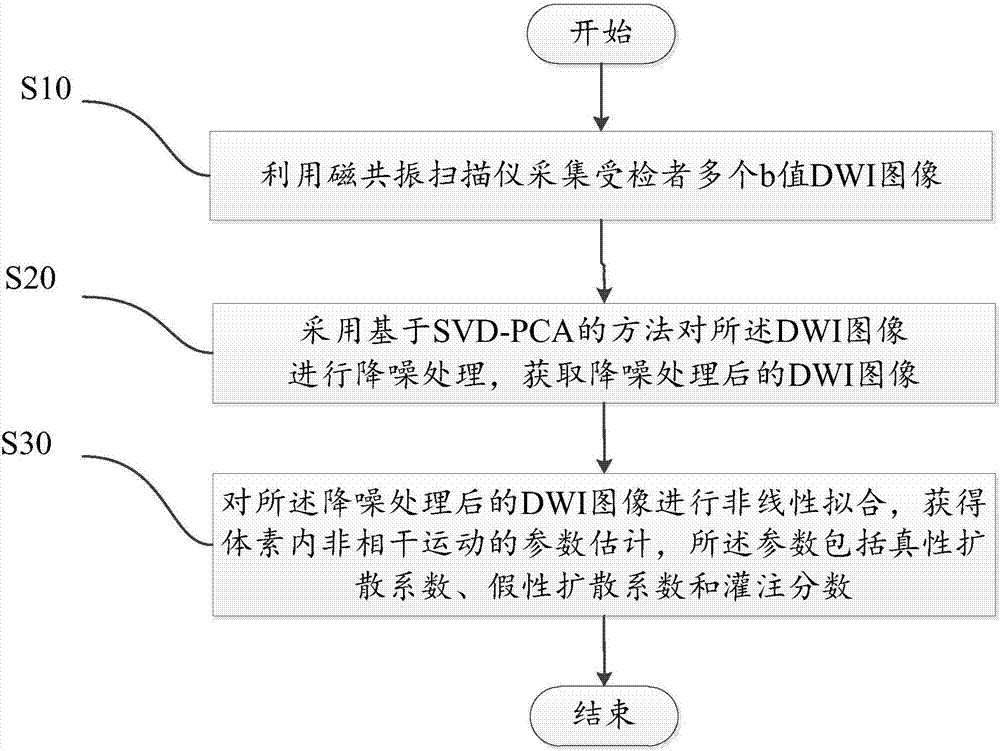
图1为本发明的扩散加权成像方法流程图；

图2为本发明施加的扩散敏感梯度场示意图；

图3为本发明实施例一不同阈值所对应的重建图像间的均方差曲线示意图；

图4为本发明dwi成像方法获得假性扩散系数图；

图5为本发明dwi成像方法获得的真性扩散系数图；

图6为本发明dwi成像方法获得的灌注分数图。

【具体实施方式】

为使本发明的上述目的、特征和优点能够更为明显易懂，下面结合附图和实施例对本发明的具体实施方式做详细的说明。

如图1所示，本发明的扩散加权成像方法主要包括：

s10、利用磁共振扫描仪采集受检者的多个b值dwi图像。水分子在介质中的随机运动称为扩散，当梯度磁场存在时，水分子的扩散引起横向磁化矢量的失相位，引起mr信号降低。dwi可以观察水分子的扩散特性，为增加扩散的敏感性，需施加扩散敏感梯度，施加的扩散敏感梯度可与自旋回波(spinecho，se)、平面回波成像(echoplanarimaging，epi)、快速自旋回波(fastspinecho，fse)、梯度回波序列(gradientechopulsesequence，gre)等脉冲序列融合，并可显著增加脉冲序列对水分子布朗运动的敏感性。扩散梯度包含两个扩散敏感梯度场，如图2所示在se序列基础上，两个极性和大小均相同的扩散敏感梯度场位于180°脉冲的两侧对称位置。对于弥散速度慢的水分子，第一个梯度脉冲所致的质子自旋去相位会被第二个梯度脉冲再聚集，信号不降低；而对于弥散速度快的水分子，第一个梯度脉冲所致的质子自旋去相位离开了原来的位置，不能被第二个梯度脉冲再聚集，信号降低，从而形成dwi上的信号差别。弥散加权的程度用弥散敏感因子b表示，代表弥散敏感梯度场强的大小，而dwi是在某一b值下测得的信号强度成像，其中，b值的物理计算公式为：b＝γ²g²δ²(δ-δ/3)，其中，γ为磁旋比，g、δ、δ分别代表施加的两个扩散敏感梯度场的幅度、持续时间及间隔时间。本实施例中，在梯度方向上施加弥散梯度，获取b值分别为b0＝0s/mm²，b1＝10s/mm²，b2＝20s/mm²，b3＝40s/mm²， b4＝60s/mm²，b5＝80s/mm²，b6＝110s/mm²，b7＝140s/mm²，b8＝170s/mm²，b9＝200s/mm²，b10＝300s/mm²，b11＝400s/mm²，b12＝500s/mm²，b13＝600s/mm²，b14＝700s/mm²，b15＝800s/mm²，b16＝900s/mm²，b17＝1000s/mm²等18个不同的弥散敏感因子在受检者脑部的dwi图像。

需要说明的是：当施加扩散敏感梯度时，b值越高，dwi对于水分子的运动越敏感，但组织信号衰减也越明显，过高的b值得到的dwi信噪比(snr)很低；在机器硬件条件一定的情况下，b值增高必然会延长回波时间，从而进一步降低snr。较小的b值得到的图像信噪比高，但是对水分子扩散运动的检测不敏感，而且组织信号的衰减受诸如组织血液灌注中水分子运动、各种生理运动、细胞本身结构、组织特性、温度等各种因素的影响，这些运动模式相对于水分子的扩散运动来说要明显得多。因此本发明采用双指数模型来分析不同b值下dwi信号衰减的规律。由ivim理论：

sb/s0＝(1-f)·exp(-bd)+f·exp[-b(d+d^*)](1)

其中，s代表体素内的信号强度；d代表体素内真性水分子扩散，称为真性扩散系数；d*代表体素内微循环灌注，称为假性扩散系数(pseudodiffusioncoefficient)；f表示灌注分数(perfusionfraction)，代表体素内微循环灌注效应占总体扩散效应的容积率。需要说明的是，本实施例中，无需对所有dwi图像进行数据采样平均，对于dwi图像可进行一定的预处理：对图像进行合理的重采集以及配准，实现数据的优化；利用四邻域方法对优化后的图像进行平滑，以消弱图像中极值的影响。

s20、采用基于奇异值分解(singularvaluedecomposition，svd)与主成分分析(principalcomponentanalysis，pca)的方法对上述dwi图像进行降噪处理，获取降噪处理后的dwi图像。在本发明一实施例中，分别对每个b 值dwi图像采用基于奇异值分解与主成分分析svd-pca的方法进行降噪处理，具体过程包括：

(a)将任一b值dwi图像分解成若干个图像块，其中相邻图像块之间存在重叠的部分。在本实施例中，以b0值dwi图像为例说明：采用滑动窗口对该dwi图像作有重叠的分块分解，每次窗口滑动都会在窗口包含的图像区域产生一个图像块，且窗口滑动不存在跳跃的现象，这样分解产生的相邻图像块之间存在部分重叠，最终单个dwi图像会形成m个小图像块。需要说明的是，对于相邻图像块重叠的部分，可进行均值处理，重叠区域的图像像素值为两次窗口滑动采集的平均值或者加权处理后的均值，有利于消除窗口滑动产生的块效应。

(b)将所有图像块展成(转换或者转化成)矢量组成矢量合成矩阵。各个图像块由同一窗口滑动分解获得，因此各个图像块包含的像素点的数目相同，每个图像块展成或者转化为矢量后的元素数也相同。设第一个图像块转化的矢量为{a11，a12，a13，…，a1n}，第2个图像块转化的矢量为{a21，a22，a23，…，a2n}，则第m个图像块转化的矢量为{am1，am2，am3，…，amn}。以其中一个图像块转化的矢量作为矢量合成矩阵的行，则该dwi的所有图像块转化的矢量可组成m×n的矢量合成矩阵c，矢量合成矩阵的行数等于该dwi图像分解的图像块数，即矢量合成矩阵是m个n维向量，m>n。

(c)对矢量合成矩阵作奇异值分解，获取矢量合成矩阵中各基矢量的分量值。对于矢量合成矩阵c作svd，可写成c＝u*s*v^t(即矢量合成矩阵c可分解为三个矩阵之积)，其中u为m×m的矩阵，u的列是cc^t的正交特征向量；v为n×n的矩阵，v的列是c^tc的正交特征向量；s为m×n的奇异值矩阵，且s为对角矩阵，对角元素为从大到小排列的特征值，也可称为矢量 合成矩阵中各基矢量的分量值。更详细地，s是矢量合成矩阵c的奇异值构成的对角矩阵，s＝diag(λ1，λ2，…λi…，λp)，其中,λi为矢量合成矩阵c的奇异值，λ1≥λ2≥…≥λi…≥λp，且p<n。

在上述svd分解过程中，可以认为(u、v)是一组正交变换基对，而奇异值则是变换系数。大的奇异值对应图像块在变换域中的低频部分，小的奇异值对应着图像块在变换域中的高频部分。在图像中，高频部分对应着图像纹理细节和噪声。通过设定一个合适的阈值，滤除较小的奇异值，保留较大的奇异值，则可起到去噪的结果。

(d)根据设定阈值对分量值进行过滤处理获取去噪后的合成矩阵，并对去噪后的合成矩阵作svd反变换获取去噪后的dwi图像。在本发明实施例中，分别采用不同阈值对各分量值进行过滤处理，重建合成矩阵，其中对大于或等于阈值的分量值保留，对小于阈值的分量作置零处理；根据不同阈值对应的合成矩阵作svd反变换，获得不同阈值所对应的dwi重建图像；计算不同阈值所对应的重建图像间的均方差并获取均方差曲线；在均方差曲线上出现峰值位置的前端所对应的阈值选定为设定阈值。如图3所示为本实施例中获得的均方差曲线，其中横坐标表示经过过滤处理的合成矩阵中非零奇异值的个数，纵坐标表示对应合成矩阵反变换后得到的dwi重建图像间的均方差，从图可看出，当合成矩阵的非零奇异值个数在7-11之间变化时，dwi重建图像间的均方差在45-60之间波动，说明dwi重建图像的内容基本没有变化；当合成矩阵的非零奇异值个数减小到6个时，dwi重建图像间的均方差处于峰值或最大峰值(本实施例中约为130)，远高于合成矩阵的非零奇异值个数为7时的均方差。因此，在本实施例中，选定均方差曲线上峰值或最大峰值位置后端所对应的阈值即第7个非零奇异值为设定阈值。在通过上述过程获得设定阈值后，对 经过奇异值分解的基矢量的各个分量值进行去噪处理，其中：对小于设定阈值的分量作置零处理，并保留大于或等于设定阈值的分量。按照上述过程可获得所有b值dwi图像去噪处理后的图像。

s30、对降噪处理后的dwi图像进行非线性拟合，获得体素内非相干运动的参数估计，其中参数估计包括d真性扩散系数估计、d*假性扩散系数估计和f灌注分数估计。由于d*值显著大于d值，常高于d值数十个数量级，因此，应用低b值dwi(通常指b<200s/mm²)测量到的信号衰减主要反映灌注效应，高b值dwi(b＝200-1000s/mm²)测量到的信号衰减主要反映水分子扩散。根据上述分析，在本发明一实施例中，采用levenberg-marquardt对所述降噪处理后的dwi图像进行分段非线性拟合，其中采用高b值dwi图像估计真性扩散系数，采用全部b值dwi图像估计假性扩散系数和灌注分数。需要说明的是：为保证保证所有参数图的非负性，本实施例中采用变量代换，即令d*＝(d*)²,d＝(d)²,f＝(f)²，采用levenberg-marquardt对d*,d和f进行非线性拟合，从而确保d*图，d图，以及f图都是正值，其中d*、d、f分别是代换变量。

单独的噪声图像块信息有限，对其进行处理不能很好的将信号从噪声中分离出来。本发明的扩散加权成像方法，在采用svd-pca的方法对dwi图像进行降噪处理时，可将所有b值dwi图像分为若干组，每组至少包含两个不同b值dwi图像，对每组的dwi图像进行滑动窗口分解为多个图像块，且属于同一组的图像块经矢量转换后共同组成矢量合成矩阵，采用如实施例一类似的方法对每组的矢量合成矩阵进行去噪处理。需要说明的是，在每组的矢量合成矩阵中，属于同一个b值dwi图像的不同图像块展成的矢量对应矢量合成矩阵的不同行，不同b值dwi图像中相同位置的图像块展成的矢量串接对应 矢量合成矩阵的同一行。为有效去除噪声的干扰，在本发明实施例二中，采用基于奇异值分解与主成分分析svd-pca的方法对上述dwi图像进行降噪处理，获取降噪处理后的dwi图像具体步骤为：

(a)将所有b值dwi图像分解成若干个图像块，其中相邻图像块之间存在重叠的部分。在本实施例中，采用滑动窗口分别对b0-b17等18个b值dwi图像作有重叠的分块分解，每次窗口滑动都会在窗口包含的图像区域产生一个图像块，且窗口滑动不存在跳跃的现象，这样分解产生的相邻图像块之间存在部分重叠，本实施例中每个b值dwi图像会形成m个图像块。需要说明的是，对于相邻图像块重叠的部分，可进行均值处理，重叠区域的图像像素值为两次窗口滑动采集的平均值或者加权处理后的均值，有利于消除窗口滑动产生的块效应。

(b)将所有图像块展成矢量组成矢量合成矩阵。所有b值dwi的图像块由同一窗口滑动分解获得，因此各个图像块包含的像素点的数目相同，每个图像块转化为矢量后的元素数也相同。与实施例一不同之处在于：对于同一b值dwi图像，不同图像块转化的矢量分布在矢量合成矩阵的不同行；对于不同b值dwi图像，属于同一滑动窗口的对应图像块转化成的矢量串接在矢量合成矩阵的同一行。如b0值dwi图像由窗口滑动形成的第一图像块转化为矢量{a11，a12，a13，a14}，b1值dwi图像由窗口滑动形成的第一图像块转化为矢量{b11，b12，b13，b14}，依次类推bx(bx≤b17)值dwi图像由窗口滑动形成的第一图像块转化为矢量{x11，x12，x13，x14}，则矢量合成矩阵的第一行可表示为{a11，a12，a13，a14，b11，b12，b13，b14，…，x11，x12，x13，x14，…}。对于合成矩阵作奇异值分解获取各基矢量的分量值，以及根据设定阈值对分量值进行过滤处理获取去噪后的合成矩阵具体方法可参考实施例一。

作为对比，本发明在实施例三中对利用磁共振扫描仪采集的受检者多b值dwi图像未采用降噪处理，且所有b值dwi图像都没有做采样平均，而直接levenberg-marquardt方法进行非线性拟合获取计算参数值，且各参数估计值为计算参数值的平方。如图4为采用本发明dwi成像方法获得的假性扩散系数图，其中图4a对应实施例一，图4b对应实施例二，图4c对应实施例三，不同灰度值代表不同的信号估计强度，采用svd-pca进行去噪处理获取的假性扩散系数图中孤立点或估计错误点(图中亮度值较高的白点)的个数明显少于仅采用levenberg-marquardt方法获得的假性扩散系数图，说明采用svd-pca进行前期处理可明显提高假性扩散系数估计的正确率。此外，dwi图像噪声不仅导致图像在空间的波动，也导致同一像素在b值分布方向的的波动，因此看出对每个b值dwi图像单独去噪与对所有b值dwi合成矩阵作去噪效果是不一样的，且对所有b值dwi合成矩阵采用svd-pca获得的假性扩散系数图中出现孤立点的个数更少，去噪的效果更好，假性扩散系数估计的正确率更高。如图5为采用本发明dwi成像方法获得的真性扩散系数图，其中图5a对应实施例一，图5b对应实施例二，图5c对应实施例三，由于本发明在利用levenberg-marquardt进行参数拟合过程中采用了变量替换，保证了所有参数的非负性，无论是否采用svd-pca进行去噪处理，真性扩散系数图都仅有部分孤立点或估计错误点。更进一步地，与图5c相比，图5a中采用svd-pca进行前期处理进一步提高了真性扩散系数估计的正确率。如图6为采用本发明dwi成像方法获得的灌注分数图，其中图6a对应实施例一，图6b对应实施例二，图6c对应实施例三。对比图6a和图6c，所有b值dwi合成矩阵采用svd-pca进行去噪处理获取的灌注分数图中孤立点或估计错误点(图中亮度较高的白点)的个数明显少于仅采用levenberg-marquardt方法获得的灌注 分数图。对比图6a与图6b，对每个b值dwi图像单独去噪获取的灌注分数图中孤立点或估计错误点的个数，ivim参数估计的可靠性明显提高。

以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。