基于静应变极值预测的铁路钢桥静载性能评估方法与流程

本发明涉及铁路钢桥静载性能评估领域，具体涉及一种基于静应变极值预测的铁路钢桥静载性能评估方法。

背景技术：

铁路钢桥的静载性能直接关系到铁路列车的运营安全，若在环境荷载作用下铁路钢桥的关键构件超过最大允许值而未能及时发现和整治，会十分危险，甚至发生梁断车毁的灾难性事件，因此开展铁路钢桥的静载性能评估工作具有重要意义。

目前，已有研究工作者针对铁路钢桥关键构件的应变状态进行重点监测，并选取监测数据的应变极值与理论设计最大值比较，从而判断现阶段铁路钢桥的静载性能。然而这一种方法存在一个缺点，即有限监测数据的应变极值不能代表铁路钢桥在整个运营期内的应变极值，因此无法实现对铁路桥梁在整个服役期内的静载性能评估。另有研究工作者尝试利用监测数据应变极值的概率统计特性对铁路桥梁在整个服役期内的静载性能进行评估，但此方法仍存在两个问题有待解决：(1)所采用的应变极值是一天内应变曲线的最大值和最小值，但一天内应变曲线的最大值和最小值并不一定是极值，即有可能是应变曲线的端点值，因此提取的应变极值数据不够准确；(2)应变极值的概率统计特性采用概率密度函数来描述，然而概率密度函数与应变极值概率密度柱状图的柱条宽度有关，导致概率密度函数失去唯一性。

技术实现要素：

针对现有技术中存在的缺陷，本发明的目的在于提供一种名称。

为达到以上目的，本发明采取的技术方案是：一种基于静应变极值预测的铁路钢桥静载性能评估方法，该方法包括如下步骤，

步骤a.在采样时间L天内采集铁路桥梁关键构件受力最不利位置的应变数据；

步骤b.利用小波包分析方法提取所述应变数据中的静应变成分；

步骤c.以天为单位对所述静应变成分进行划分，对每天内的所有静应变值按照采集先后顺序做一阶差分处理，得到静应变值在每天的差分序列，将每一天内的所述差分序列任意分割为多份，并对每一份所述差分序列各自求和，再对每一份所述差分序列的求和结果取绝对值并相加求得总和，在分割份数相同的情况下比较在不同分割点下求得的所述总和的大小，确定所述总和最大时的分割点，比较所述差分序列在所述总和最大时的分割点下的大小，从而确定每天内所述静应变成分中日变化极大值和日变化极小值，进而确定并比较所述采样时间L天内所述静应变成分中日变化极大值D_MAX和日变化极小值D_MIN；

步骤d.利用广义极值分布函数G(D_MAX)和F(D_MIN)分别拟合所述采样时间L天内所述静应变成分中日变化极大值D_MAX和日变化极小值D_MIN的累加分布特性：

步骤e.对所述铁路桥梁关键构件受力最不利位置进行静载性能评估：其中，

式中，P为超越概率，利用牛顿迭代法并结合所述广义极值分布函数G(D_MAX)和F(D_MIN)，求解方程(4)和方程(5)，确定超越概率为P时的静应变标准值和

用表示和中的绝对值最大者，将与设计允许值比较判断所述铁路桥梁的静载性能，若则所述铁路桥梁关键构件受力最不利位置的静载性能处于安全状态；反之，则所述铁路桥梁关键构件受力最不利位置的静载性能处于非安全状态。

在上述技术方案的基础上，所述步骤a中采用光纤光栅应变传感器采集所述应变数据，并以光纤光栅温度传感器作为温度补偿。

在上述技术方案的基础上，所述步骤a中采样时间L大于200天，且采样频率大于1/600Hz小于1Hz。

在上述技术方案的基础上，所述小波包分析方法具体包括将采集到的所有所述应变数据按照采集先后顺序构成应变序列，后将所述应变序列进行第c个尺度上的小波包分解，得到2^c个小波包系数，提取出第一个小波包系数并对其重构，得到所述应变序列中的静应变成分，其中c为测量点个数系数。

在上述技术方案的基础上，所述测量点个数系数c等于5。

在上述技术方案的基础上，所述步骤c中的每一天的差分序列被任意分割为三份。

在上述技术方案的基础上，所述采样时间L天内所述静应变成分中日变化极大值D_MAX的累加分布特性的拟合包括，计算所述日变化极大值D_MAX的累加概率值，并利用所述广义极值分布函数G(D_MAX)对其拟合，其中：

式中，b、d和r分别表示G(D_MAX)的尺度参数、位置参数和形状参数，将计算求得的日变化极大值D_MAX和日变化极大值D_MAX的累加概率值分别代入式(2)中，利用最小二乘法确定b、d和r的最佳取值；

所述采样时间L天内所述静应变成分中日变化极小值D_MIN的累加分布特性的拟合包括，计算所述日变化极小值D_MIN的累加概率值，并利用所述广义极值分布函数F(D_MIN)对其拟合，其中

式中，g、h和λ分别表示F(D_MIN)的尺度参数、位置参数和形状参数，将计算求得的日变化极小值D_MIN和日变化极小值D_MIN的累加概率值分别代入式(3)中，利用最小二乘法确定g、h和λ的最佳取值；

在上述技术方案的基础上，所述超越概率P的取值为0.01。

与现有技术相比，本发明的优点在于：

(1)本发明中的基于静应变极值预测的铁路钢桥静载性能评估方法，其利用一阶差分确定应变极值，从而有效避免应变最大值或最小值不是应变极值的情况，使得提取的应变极值数据更加准确。

(2)本发明中的基于静应变极值预测的铁路钢桥静载性能评估方法，其利用累加概率值克服了传统方法中概率统计特性没有唯一性的缺点，保证了应变极值概率统计特性的唯一性，而且本方法更能准确有效地对铁路桥梁在整个服役期内的静载性能评估，可得到广泛推广和应用。

附图说明

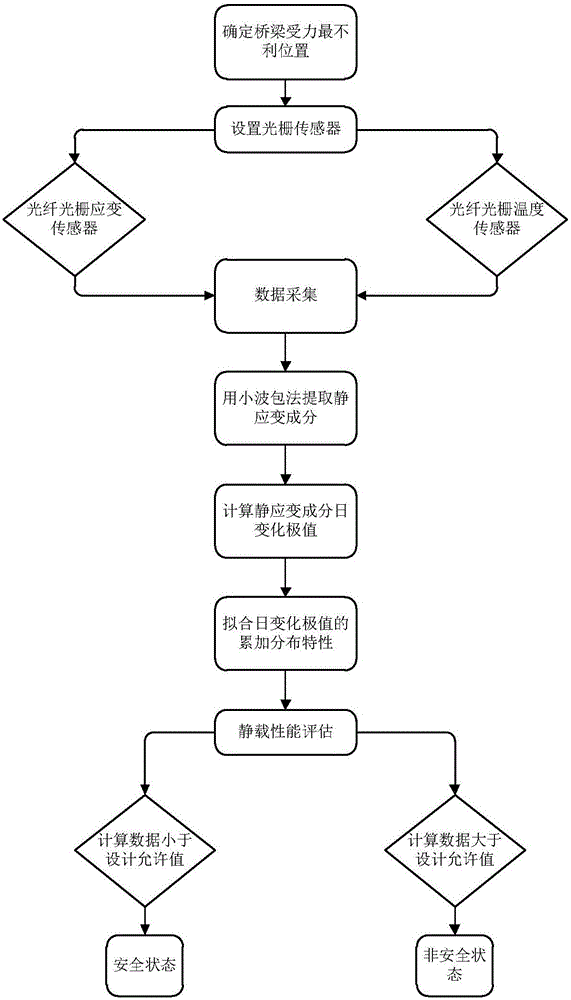
图1本发明中评估方法的流程图；

图2为本发明实施例中大胜关长江大桥的立面图；

图3为本发明实施例中光纤光栅应变传感器的布置位置；

图4为本发明实施例中所有应变值按照采集先后顺序构成的应变序列；

图5为本发明实施例中应变序列中的静应变成分；

图6为本发明实施例中日变化极大值的变化曲线；

图7为本发明实施例中日变化极小值的变化曲线；

图8为本发明实施例中日变化极大值广义极值分布的拟合结果；

图9为本发明实施例中日变化极小值广义极值分布的拟合结果。

图中：1-上弦杆，2-光纤光栅温度传感器。

具体实施方式

以下结合附图及实施例对本发明作进一步详细说明。

本发明提供一种基于静应变极值预测的铁路钢桥静载性能评估方法，参见图1所示的流程图，该方法包括以下步骤：

步骤a.对铁路桥梁关键构件的最不利位置进行应变数据采集：

本发明将光纤光栅应变传感器配接到数据采集系统中，并以光纤光栅温度传感器作为温度补偿，对铁路桥梁关键构件的最不利位置进行数据采集，受力最不利位置指的是桥梁受力最大、最集中处或桥梁结构最为容易破坏处。采样频率表示为fHz，采样时间长度用L表示，采集到的第i个应变值采用S(i)表示，i＝1,...,M，M为应变值总个数。其中，采样频率大于1/600Hz小于1Hz，采样时间L大于200天。

步骤b.利用小波包分析方法提取应变数据中的静应变成分：

由于应变数据明显受到列车荷载的干扰，因此利用小波包分析方法提取出应变数据中不受列车荷载干扰的静应变成分。其中小波包分析方法是一种信号处理与分析的常用方法，可以根据信号特性和分析要求自适应地选择相应频带与信号频谱相匹配，是一种精细的信号分解方法，其具体操作为：将采集到的所有应变值S(i)按照采集先后顺序构成应变序列，后将应变序列进行第c个尺度上的小波包分解，得到2^c个小波包系数，提取出第一个小波包系数并对其重构，得到应变序列中的静应变成分，其中c为测量点个数系数。

步骤c.利用一阶差分获取静应变成分中的日变化极值：

1.以天为单位对静应变成分进行划分，静应变成分在第m天内的第j个静应变值采用S_m(j)表示，其中m＝1,2,...,L，j＝1,2,...,N_m，N_m为静应变值在第m天内的总个数。

2.对每天内的所有静应变值按照采集先后顺序做一阶差分处理，一阶差分处理指的是静应变值中连续相邻两项之差，从而得到静应变值在每天内的差分序列。其中差分序列在第m天内的第k个值采用D_m(k)表示，k＝1,2,...,N_m-1。

3.每一天的差分序列可以根据需要被任意分割为多份，本发明中的差分序列被分割为三份，为了归纳说明，本发明将第m天内的差分序列{D_m(1),D_m(2),...,D_m(N_m-1)}分割为三份，其中第一份差分序列为{D_m(1),D_m(2),...,D_m(p_1,m)}，第二份差分序列为{D_m(p_1,m+1),D_m(p_1,m+2),...,D_m(p_1,m+p_2,m)}，第三份差分序列为{D_m(p_2,m+1),D_m(p_2,m+2),...,D_m(N_m-1)}，其中p_1,m、p_2,m分别为第m天内差分序列的两个分割点，且满足1＜p_1,m＜p_2,m＜N_m-1。

4.对三份差分序列中的所有值求和，用Z_m,l(p_1,m,p_2,m)表示第m天内取值为p_1,m,p_2,m时第l份差分序列之和，其中l＝1,2,3，然后按照下式求得Z_m,1(p_1,m,p_2,m)、Z_m,2(p_1,m,p_2,m)和Z_m,3(p_1,m,p_2,m)三者之和：

Q_m(p_1,m,p_2,m)＝|Z_m,1(p_1,m,p_2,m)|+|Z_m,2(p_1,m,p_2,m)|+|Z_m,3(p_1,m,p_2,m)| (1)

式中，Q_m(p_1,m,p_2,m)的计算结果与p_1,m，p_2,m取值有关，对p_1,m，p_2,m选取在约束条件1＜p_1,m＜p_2,m＜N_m-1下所有可能的取值，代入式(1)中计算出相应的Q_m(p_1,m,p_2,m)值，所有Q_m(p_1,m,p_2,m)值中必然存在一个最大值，假设此最大值是由p_1,m＝a_1,m、p_2,m＝a_2,m得到的，则第m天内静应变成分中的日变化极大值为D_m(a_1,m)和D_m(a_2,m)两者中的较大值，日变化极小值为D_m(a_1,m)和D_m(a_2,m)两者中的较小值，在确定出第m天内静应变成分中的日变化极大值和极小值后，通过比较每天的日变化极大值和极小值，从而确定在所有天数L内的日变化极大值和极小值，其中所有天数L内的日变化极大值采用D_MAX表示，所有天数L的日变化极小值采用D_MIN表示。

本发明利用一阶差分确定应变极值，从而有效避免应变最大值或最小值不是应变极值的情况，使得提取的应变极值数据更加准确。

步骤d.利用广义极值分布函数拟合日变化极值的累加分布特性：

1.计算日变化极大值D_MAX的累加概率值，在概率与数理统计理论中，累加概率值定义为统计变量不超过某一数值的发生概率，并利用广义极值分布函数对其拟合：

式中，G(D_MAX)表示的广义极值分布函数，b、d和r分别表示G(D_MAX)的尺度参数、位置参数和形状参数，将计算求得的日变化极大值和日变化极大值D_MAX的累加概率值分别代入式(2)中并利用最小二乘法确定b、d和r的最佳取值；

2.计算日变化极小值的累加概率值，并利用广义极值分布函数对其拟合：

式中，F(D_MIN)表示的广义极值分布函数，g、h和λ分别表示F(D_MIN)的尺度参数、位置参数和形状参数，将计算求得的日变化极小值和日变化极小值D_MIN的累加概率值分别代入式(3)中并利用最小二乘法确定g、h和λ的最佳取值。

步骤e.对所述铁路桥梁关键构件受力最不利位置进行静载性能评估：

利用牛顿迭代法求解方程(4)和方程(5)，确定超越概率为P时的静应变标准值和超越概率指在一定时期内，可能遭遇大于或等于给定参数值的概率。

用表示和中的绝对值最大者，将与设计允许值比较判断所述铁路桥梁的静载性能，若则所述铁路桥梁关键构件受力最不利位置的静载性能处于安全状态；反之，则所述铁路桥梁关键构件受力最不利位置的静载性能处于非安全状态。

牛顿迭代法是一种求解方程根的重要方法，其最大优点是在方程或的单根附近平方收敛；按照铁路桥梁的100年设计服役期考虑，超越概率P的取值为0.01。

下面以大胜关长江大桥的弦杆轴向应变为例，说明本发明的具体实施过程。

参见图2所示大胜关长江大桥的立面图，以及图3所示光纤光栅应变传感器布置位置示意图，将光纤光栅应变传感器2安装在大胜关长江大桥跨中边桁上弦杆1的轴向位置，并配接到数据采集系统中，以光纤光栅的温度传感器作为温度补偿，对上弦杆1轴向应变进行数据采集。采样频率f为1Hz，采样时间长度L为232天，采集到的第i个应变值采用S(i)表示，i＝1,...,33408。

参见图4所示，其为大胜关长江大桥所有应变值S(i)按照采集先后顺序构成的应变序列。

参见图5所示，将应变序列进行第5个尺度上的小波包分解，得到32个小波包系数，提取出第一个小波包系数并对其重构，得到应变序列中的静应变成分。

以天为单位对静应变成分进行划分，静应变成分在第m天内的第j个静应变值采用S_m(j)表示，其中m＝1,2,...,232，j＝1,2,...,144。对每天内的所有静应变值按照采集先后顺序做一阶差分处理，得到静应变值在每天内的差分序列，差分序列在第m天内的第k个值采用D_m(k)表示，k＝1,2,...,143。

根据上述步骤c中的第3和第4步确定232天内的日变化极大值D_MAX和日变化极小值D_MIN，分别参见图6和图7所示。根据步骤d中相关计算步骤，利用最小二乘法确定b、d和r以及g、h和λ的最佳参数取值，其中b＝41.3228、d＝33.0127、r＝-0.4071；g＝54.4519、h＝-24.6663、λ＝-0.612298，代入各个数值计算得到日变化极大值广义极值分布的拟合结果和日变化极小值广义极值分布的拟合结果，分别参见图8和图9所示。

利用牛顿迭代法对上述步骤e中的方程(4)和方程(5)求解，确定具有超越概率为P的静应变标准值和其中：超越概率P为0.01。

计算结果为：然后选取和中的最大绝对值，即将与设计允许值比较判断铁路桥梁的静载性能：已知大胜关铁路桥梁钢材选用Q420，则可知则关键构件受力最不利位置的静载性能处于安全状态。

本发明不局限于上述实施方式，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也视为本发明的保护范围之内。本说明书中未作详细描述的内容属于本领域专业技术人员公知的现有技术。