基于S形模型的工业部门终端能源需求预测方法与流程

本发明涉及一种定量的工业部门终端能源需求预测方法，具体涉及一种基于人均GDP与人均工业部门终端能源消费间的“S”形理论模型，运用趋势分析法以及双曲正切函数数学方法构建其预测方程的方法以及基于该预测方程的工业部门终端能源需求预测方法。

背景技术：

与一次能源消费不同，部门终端能源消费是该部门一次能源消费减去能源加工、转化和储运环节损失后的部门终端能源消费，二者间存在着能源转化效率(即加工、转化和储运等中间环节效率)和终端利用效率问题。工业部门是终端能源消费中主要的三大部门之一，占比34％以上，中国甚至达到了70％。目前，工业部门的能源需求预测方法主要是部门预测法。部门预测法是在系统总结不同部门终端能源消费历史数据和部门发展间相互关系的基础上，通过对各部门及细分部门未来发展趋势的判定，预测部门乃至国家能源需求。其主要缺陷表现在：一方面涉及的基础资料、数据庞杂，收集、统计终端部门数据涉及的细分部门范围广，极易产生统计性偏差；其二，部门终端能源需求预测中对部门未来发展的判断往往源于对以往历史数据的推演，缺乏对部门终端能源消费基本规律的把握，从而极易产生预测偏差；世界上著名的能源机构IEA和EIA，就是使用这一方法进行能源需求预测的。其历史预测结果检验表明，典型发展中国家和地区的预测结果大多存在10％以上误差。

此外，《基于“S”形模型的能源需求预测方法》是建立在人均GDP与人均 能源消费间“S”形理论模型基础上，运用数学方法构建的一种一次能源需求定量预测技术与方法。历史预测结果检验表明，其对国家或地区的一次能源需求预测准确性更高、更切合实际。但是，该方法只适用于一次能源需求预测，对部门终端能源需求预测并不适用。一方面，并非所有的部门终端能源消费遵循“S”形规律；另一方面，对于满足“S”形规律的工业部门终端能源消费，其模型参数与一次能源消费“S”形模型参数也不一致。

传统的部门能源预测方法缺陷的核心是缺乏对部门终端能源消费与经济发展间长尺度定量关系的把握，仅用以往数据模拟、推演或类比未来，预测缺乏科学性和准确性，结果偏差大。提高建立在部门终端能源消费与经济发展间定量关系基础上的中长期部门终端能源需求预测的准确性、客观性对科学制定国家规划、未来能源行业发展以及部门政策制定具有重要的意义。

技术实现要素：

为克服现有技术的不足，提供一种结果更精确的工业部门终端能源需求预测方法，本发明提供一种基于S形模型的工业部门终端能源需求预测方法，以人均工业部门终端能源消费与人均GDP间的“S”形理论模型为基础，以人均GDP为自变量，并运用趋势分析法以及双曲正切函数数学方法，结合不同国家或区域的历史数据建立工业部门终端能源需求预测方程，从而实现对国家或地区的中长期工业部门终端能源需求预测，形成了全新的工业部门终端能源需求预测方法，是对基于“S”形模型的能源需求预测方法的进一步补充、提升和延伸，其包括如下步骤：

S1：收集各国工业部门终端能源消费、人口及GDP历史数据并计算人均工业部门终端能源消费和人均GDP，以人均GDP为横坐标，人均工业部 门终端能源消费为纵坐标构建“S”形关系曲线；

S2：构建人均工业部门终端能源消费与人均GDP的“S”形物理模型；

S3：构建人均工业部门终端能源消费与人均GDP的“S”形理论模型(其理论模型可以对物理模型中三个关键点的进一步解释，以及，在预测方法预测过程中，对预测对象国家或地区人均工业部门终端能源消费与人均GDP关系曲线所处位置判定提供依据。)；

S4：构建“S”形曲线数学模型：在人均工业部门终端能源消费与人均GDP的“S”形理论模型的基础上，运用趋势分析法和双曲正切数学方法构建以人均GDP为自变量的工业部门终端能源需求预测方程，即“S”形曲线的趋势性拟合方程；

S5：预测：按照预测流程给定预测时长及相关的GDP值和人口，并计算人均GDP；

S6：将步骤S5得到的人均GDP值代入步骤S4中得到的方程中，求得不同国家/地区的工业部门终端能源需求预测结果；

其中，所述步骤S2包括：

S21：根据峰值时人均工业部门终端能源消费的高低判断国家工业部门终端能源消费所属的“S”形曲线类型；

S22：根据人均工业部门终端能源消费增速的变化规律确定“S”形曲线上的三个关键点：人均工业部门终端能源消费进入加速增长期的起飞点，人均工业部门终端能源消费增速由大到小的转折点以及人均工业部门终端能源消费增速为零或开始为负增长的零增长点；

S23：根据三个关键点分别将“S”形曲线划分为四个区间：缓慢增长区、加速增长区、减速增长区以及零/负增长区；

其中，所述步骤S3包括：

S31：搜集二产比例(即第二产业比例，是指第二产业增加值占GDP的比例)、城市化率以及钢铁消费等数据，并计算人均钢铁消费；

S32：分析“S”形曲线关键点与二产比例、城市化率以及人均钢铁消费之间的对应关系。

其中，所述步骤S4包括如下步骤：

S41：采用趋势分析方法，构建人均工业部门终端能源消费E与人均GDP值G的非平坦式方程式：

$E-E_i=A\frac{\exp \left({\mathrm{\α}}_1\right(G-G_i))-\exp (-{\mathrm{\α}}_3(G-G_i))}{2\cosh \left({\mathrm{\α}}_2\right(G-G_i))}---\left(1\right)$

其中，α₁、α₂、α₃为指数常数，单位与G^-1相同；E_i、G_i分别为曲线在转折点对应的人均工业部门终端能源消费和人均GDP值；A为趋势关系方程(1)的振幅值，单位与G相同；

S42：由方程(1)得曲线在起飞点前、转折点临近区域、零增长点后线性变化的方程分别为：

E-E_i＝A+A(α₂-α₃)(G-G_i)＝A+ρ_l(G-G_i) (2)

E-E_i＝0.5A(α₁+α₃)(G-G_i)＝ρ_i(G-G_i) (3)

E-E_i＝A+A(α₁-α₂)(G-G_i)＝A+ρ_v(G-G_i) (4)

其中，ρ_l、ρ_i、ρ_v分别为曲线在起飞点前、转折点临近区域、零增长点后线性变化区域的斜率值，G_v为曲线在零增长点的人均GDP值；

S43：由方程(2)～(4)得α₁、α₂、α₃诸待定常数与斜率相联系的方程分别为：

${\mathrm{\α}}_1=\frac{{\mathrm{\ρ}}_1+{\mathrm{\ρ}}_i+{\mathrm{\ρ}}_v}{2A}---\left(5\right)$

${\mathrm{\α}}_2=\frac{{\mathrm{\ρ}}_1+2{\mathrm{\ρ}}_i-{\mathrm{\ρ}}_v}{2A}---\left(6\right)$

${\mathrm{\α}}_3=\frac{-{\mathrm{\ρ}}_1+2{\mathrm{\ρ}}_i-{\mathrm{\ρ}}_v}{2A}---\left(7\right)$

同时曲线在零增长点处有：

$\tanh \left({\mathrm{\α}}_1\right(G_v-G_v\left)\right)\tanh \left({\mathrm{\α}}_2\right(G_v-G_i\left)\right)={\mathrm{\α}}_1{\mathrm{\α}}_2^{-1},\frac{dE}{dG}=0---\left(8\right);$

S44：将(5)、(6)二式代入方程(8)得到：

tanh(η₁A^-1)tanh(η₂A^-1)＝η₃ (9)

其中，

η₁＝0.5(ρ_l+ρ_i+ρ_v)(G_v-G_i) (10)

η₂＝0.5(ρ_l+2ρ_i-ρ_v)(G_v-G_i) (11)

${\mathrm{\η}}_3=\frac{{\mathrm{\ρ}}_1+{\mathrm{\ρ}}_i+{\mathrm{\ρ}}_v}{{\mathrm{\ρ}}_1+2{\mathrm{\ρ}}_i-{\mathrm{\ρ}}_v}---\left(12\right);$

S45：由具体数据给出G_i、E_i、G_v、ρ_l、ρ_i、ρ_v值，代入方程(9)中计算出A值；

S46：由方程(5)～(7)式依次计算出α₁、α₂、α₃值，得出“S”形曲线趋势性拟合方程，即工业部门终端能源需求预测方程，也即方程(1)的具体形式。

基于上述基于S形模型的工业部门终端能源需求预测方法，本发明同时提供一种美国的工业部门终端能源需求预测方法，其将美国的人均GDP代入下述方程式求得预测结果：

$E=1.68+1.63\frac{\exp \left(0.00002\right(G-11230))-\exp (-0.00018(G-11230))}{2\cosh \left(0.00024\right(G-11230))}.$

基于上述基于S形模型的工业部门终端能源需求预测方法，本发明同时提供一种加拿大的工业部门终端能源需求预测方法，其将加拿大的人均GDP代入下述方程式求得预测结果：

$E=1.76+3.5\frac{\exp \left(0.000046\right(G-11605))-\exp (-0.000051(G-11605))}{2\cosh \left(0.00019\right(G-11605))}.$

基于上述基于S形模型的工业部门终端能源需求预测方法，本发明同时提供一种英国的工业部门终端能源需求预测方法，其将英国的人均GDP代入下述方程式求得预测结果：

$E=0.68+1.35\frac{\exp \left(0.00002\right(G-7718))-\exp (-0.00014(G-7718))}{2\cosh \left(0.0002\right(G-7718))}.$

基于上述基于S形模型的工业部门终端能源需求预测方法，本发明同时提供一种法国的工业部门终端能源需求预测方法，其将法国的人均GDP代入下述方程式求得预测结果：

$E=0.61+2.5\frac{\exp \left(0.00004\right(G-6200))-\exp (-0.000\mathrm{05}(G-6200))}{2\cosh \left(0.00027\right(G-6200))}.$

基于上述基于S形模型的工业部门终端能源需求预测方法，本发明同时提供一种德国的工业部门终端能源需求预测方法，其将德国的人均GDP代入下述方程式求得预测结果：

$E=0.\mathrm{92}+2.7\frac{\exp \left(0.00003\right(G-\mathrm{9159}))-\exp (-0.000\mathrm{12}(G-9159))}{2\cosh \left(0.0004\right(G-9159))}.$

基于上述基于S形模型的工业部门终端能源需求预测方法，本发明同时提供一种日本的工业部门终端能源需求预测方法，其将日本的人均GDP代入下述方程式求得预测结果：

$E=0.77+2.3\frac{\exp \left(0.00002\right(G-\mathrm{7100}))-\exp (-0.00009(G-\mathrm{7100}))}{2\cosh \left(0.000\mathrm{16}\right(G-\mathrm{7100}))}.$

基于上述基于S形模型的工业部门终端能源需求预测方法，本发明同时提供一种意大利的工业部门终端能源需求预测方法，其将意大利的人均GDP代入下述方程式求得预测结果：

$E=0.\mathrm{48}+1.2\frac{\exp \left(0.0000\mathrm{75}\right(G-\mathrm{7300}))-\exp (-0.000\mathrm{11}(G-\mathrm{7300}))}{2\cosh \left(0.000\mathrm{19}\right(G-\mathrm{7300}))}.$

本发明还提供一种基于S形模型的工业部门终端能源需求预测方程的构建方法，其以人均工业部门终端能源消费与人均GDP的“S”形理论模型为基础，以人均GDP为自变量，运用趋势分析法以及双曲正切数学方法，结合不同国家或区域的历史数据建立工业部门终端能源需求预测方程，具体步骤如下：

S1：收集各国工业部门终端能源消费、人口及GDP历史数据并计算人均工业部门终端能源消费和人均GDP，以人均GDP为横坐标，人均工业部门终端能源消费为纵坐标构建“S”形关系曲线；

S2：构建人均工业部门终端能源消费与人均GDP的“S”形物理模型；

S3：构建人均工业部门终端能源消费与人均GDP的“S”形理论模型；

S4：构建“S”形曲线数学模型：在人均工业部门终端能源消费与人均GDP 的“S”形理论模型的基础上，运用趋势分析法和双曲正切数学方法构建以人均GDP为自变量的工业部门终端能源需求预测方程，即“S”形曲线趋势性拟合方程；

其中，所述步骤S2包括：

S21：根据峰值时人均工业部门终端能源消费的高低判断国家工业部门终端能源消费所属的“S”形曲线类型；

S22：根据人均工业部门终端能源消费增速的变化规律确定“S”形曲线上的三个关键点：人均工业部门终端能源消费进入加速增长期的起飞点、人均工业部门终端能源消费增速由大到小的转折点以及人均工业部门终端能源消费增速为零或开始为负增长的零增长点；

S23：根据三个关键点分别将“S”形曲线划分为四个区间：缓慢增长区、加速增长区、减速增长区以及零/负增长区；

其中，所述步骤S3包括：

S31：搜集二产比例、城市化率以及钢铁消费数据，并计算人均钢铁消费；

S32：分析“S”形曲线关键点与二产比例、城市化率以及人均钢铁消费之间的对应关系。

本发明一个实施例的基于S形模型的工业部门终端能源需求预测方程的构建方法，其中，所述步骤S4包括如下步骤：

S41：采用趋势分析方法，构建人均工业部门终端能源消费E与人均GDP值G的非平坦式方程式：

$E-E_i=A\frac{\exp \left({\mathrm{\α}}_1\right(G-G_i))-\exp (-{\mathrm{\α}}_3(G-G_i))}{2\cosh \left({\mathrm{\α}}_2\right(G-G_i))}---\left(1\right)$

其中，α₁、α₂、α₃为指数常数，单位与G^-1相同；E_i、G_i分别为曲线在转折点对应的人均工业部门终端能源消费和人均GDP值；A为趋势关系方程(1)的振幅值，单位与G相同；

S42：由方程(1)得曲线在起飞点前、转折点临近区域、零增长点后线性变化的方程分别为：

E-E_i＝A+A(α₂-α₃)(G-G_i)＝A+ρ_l(G-G_i) (2)

E-E_i＝0.5A(α₁+α₃)(G-G_i)＝ρ_i(G-G_i) (3)

E-E_i＝A+A(α₁-α₂)(G-G_i)＝A+ρ_v(G-G_i) (4)

其中，ρ_l、ρ_i、ρ_v分别为曲线在起飞点前、转折点临近区域、零增长点后线性变化区域的斜率值，G_v为曲线在零增长点的人均GDP值；

S43：由方程(2)～(4)得α₁、α₂、α₃诸待定常数与斜率相联系的方程分别为：

${\mathrm{\α}}_1=\frac{{\mathrm{\ρ}}_1+{\mathrm{\ρ}}_i+{\mathrm{\ρ}}_v}{2A}---\left(5\right)$

${\mathrm{\α}}_2=\frac{{\mathrm{\ρ}}_1+2{\mathrm{\ρ}}_i-{\mathrm{\ρ}}_v}{2A}---\left(6\right)$

${\mathrm{\α}}_3=\frac{-{\mathrm{\ρ}}_1+2{\mathrm{\ρ}}_i-{\mathrm{\ρ}}_v}{2A}---\left(7\right)$

同时曲线在零增长点处有：

$\tanh \left({\mathrm{\α}}_1\right(G_v-G_v\left)\right)\tanh \left({\mathrm{\α}}_2\right(G_v-G_i\left)\right)={\mathrm{\α}}_1{\mathrm{\α}}_2^{-1},\frac{dE}{dG}=0---\left(8\right);$

S44：将(5)、(6)二式代入方程(8)得到：

tanh(η₁A^-1)tanh(η₂A^-1)＝η₃ (9)

其中，

η₁＝0.5(ρ_l+ρ_i+ρ_v)(G_v-G_i) (10)

η₂＝0.5(ρ_l+2ρ_i-ρ_v)(G_v-G_i) (11)

${\mathrm{\η}}_3=\frac{{\mathrm{\ρ}}_1+{\mathrm{\ρ}}_i+{\mathrm{\ρ}}_v}{{\mathrm{\ρ}}_1+2{\mathrm{\ρ}}_i-{\mathrm{\ρ}}_v}---\left(12\right);$

S45：由具体数据给出G_i、E_i、G_v、ρ_l、ρ_i、ρ_v值，代入方程(9)中计算出A值；

S46：由方程(5)～(7)式依次计算出α₁、α₂、α₃值，得出“S”形曲线趋势性拟合方程，即工业部门终端能源需求预测方程，也即方程(1)的具体形式。

本发明提供的基于S形模型的工业部门终端能源需求预测方法，以人均工业部门终端能源消费基本规律为指导，从根本上解决了以往部门能源需求预测普遍存在的预测偏差大的问题，提高了预测可靠性和置信度。建立了一种兼具普适性和针对性的工业部门终端能源需求预测方法，预测方法实用便捷，易于实现和推广。其主要用于国家或地区中长期的工业部门终端能源需求预测，其成果可直接应用于考察国家能源消费的部门转移与能源品种的变化以及制定工业发展相关政策等领域。

附图说明

图1：基于S形模型的工业部门终端能源需求预测方法流程图；

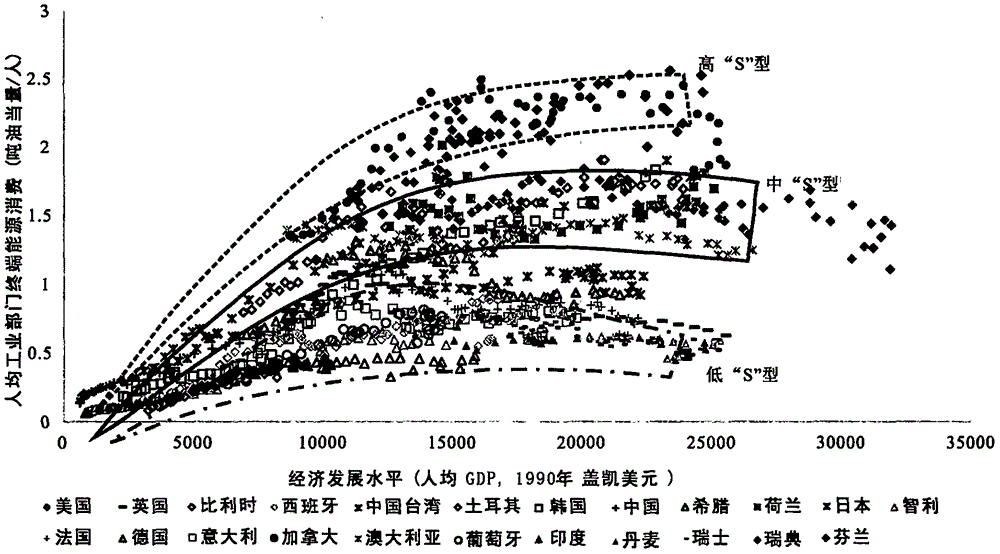
图2：各个国家的人均工业部门终端能源消费与人均GDP“S”形曲线图；

图3：人均工业部门终端能源消费与人均GDP的“S”形物理模型图；

图4：人均工业部门终端能源消费与人均GDP的“S”形理论模型图。

具体实施方式

以下将结合本发明的具体实施方式，详细陈述本发明的技术方案及其所能实现的技术效果。

图1所示为本发明的基于S形模型的工业部门终端能源需求预测方法流 程图，如图所示，本发明提供的基于S形模型的工业部门终端能源需求预测方法，主要以人均工业部门终端能源消费与人均GDP的“S”形理论模型为基础，以人均GDP为自变量，运用趋势分析法、双曲正切等数学方法，结合不同国家或区域历史数据构建工业部门终端能源消费预测方程，从而实现对国家/地区的工业部门终端能源中、长期需求的准确定量预测，其主要包括如下步骤：

S1：收集各国人口、工业部门终端能源消费及各国GDP等历史数据并计算各国人均工业部门终端能源消费及人均GDP，以人均GDP为横坐标，人均工业部门终端能源消费为纵坐标构建“S”形关系曲线：

系统总结英、美、日、德、法等11个典型发达国家/地区百余年的人均工业部门终端能源消费与人均GDP相关关系，如图2所示，为各个国家的人均工业部门终端能源消费与人均GDP的“S”形曲线图，由图可知，各个国家，随着人均GDP的增长，人均工业部门终端能源消费呈现“缓慢增长-加速增长-减速增长-零增长或负增长”的“S”形曲线。根据到达峰值时的人均工业部门终端能源消费的高低大致可以将曲线分为高(以美国、加拿大为代表)、中(以瑞典、比利时为代表)、低(以英、法、德、日、意等为代表)“S”型三类。

S2：构建人均工业部门终端能源消费与人均GDP的“S”形物理模型：

其中，步骤S2具体包括如下步骤：

S21：根据峰值时人均工业部门终端能源消费的高低判断国家工业部门终端能源消费所属的“S”形曲线类型：高“S”型峰值时的人均工业部门终端能源消费约为2～2.5toe(吨油当量)；中“S”型峰值时的人均工业部门终端能源消 费约为1.7～1.8toe；低“S”型峰值时的人均工业部门终端能源消费约为0.7～1.2toe；

S22：根据人均工业部门终端能源消费增速的变化规律确定“S”形曲线上的三个关键点：(1)起飞点，即人均工业部门终端能源消费加速增长的起始点，集中于人均GDP 2500～3000美元(1990年盖凯，下同)左右，标志着一个国家工业化社会的开始，是工业化进程、城市化进程进入加速增长期的起始点；(2)转折点，即人均工业部门终端能源消费由增速增长变成减速增长的点；(3)零增长点，即人均工业部门终端能源消费增速为零或开始负增长的点；

S23：根据三个关键点分别将“S”形曲线划分为四个区间：缓慢增长区、加速增长区、减速增长区以及零/负增长区；其中，缓慢增长区为起飞点之前的区域，加速增长区为介于起飞点和转折点之间的区域，减速增长区为介于转折点和零增长点之间的区域，零/负增长区为零增长点之后的区域，每个区域具有相对确定的工业部门终端能源需求增长方式，从而形成“S”形非线性增长预测基本原理。

请参见表1所示，为典型国家“S”形的三个转变点对应的人均GDP值，由于各国家或地区的经济发展模式存在差异，人均工业部门终端能源消费转折点和零增长点所对应的人均GDP值不尽相同：

高“S”型：呈增长快、峰值高的特征，其转折点出现在人均GDP 10000～12000美元处，零增长点出现在人均GDP为15000～17000美元处；

中“S”型：呈增长相对缓慢、峰值到来较晚的特征，其转折点出现在人均GDP 10000～12000美元处，零增长点出现在人均GDP为15000～17000美元 处；

低“S”型：呈起点低、增长慢、峰值点低等特征，其转折点出现在人均GDP 7000～8000美元处，零增长点则在人均GDP 10000～12000美元处。

表1典型国家“S”形的三个转变点对应的人均GDP值(单位：1990盖凯美元/人)

S3：构建人均工业部门终端能源消费与人均GDP的“S”形理论模型；

其中，所述步骤S3包括：

S31：搜集二产比例(即第二产业比例，是指第二产业增加值占GDP的比例)、城市化率以及钢铁消费等数据，并计算人均钢铁消费；

S32：分析“S”形曲线关键点与二产比例、城市化率以及人均钢铁消费之间的对应关系。

如图4所示，为本发明的人均工业部门终端能源消费与人均GDP的“S”形理论模型图，在人均工业部门终端能源消费与人均GDP的“S”形物理模型的基础上，通过分析“S”形曲线的三个关键点与体现出工业发展阶段、社会 财富积累和基础设施完备程度的相关指标(如二产比例、城市化率以及人均钢铁消费等)之间存在的内在联系和对应关系，构建了人均工业部门终端能源消费与人均GDP的“S”形理论模型。

由于三种类型的“S”形曲线中对应的各转折点处的GDP值不一致，而其与二产比例、城市化率以及人均钢铁消费之间的对应关系却是相似的，因此，本发明提供的图4中，将三个类型的人均工业部门终端能源消费与人均GDP的“S”形曲线的理论模型整合在了一张图上。

三个类型的人均工业部门终端能源消费与人均GDP的“S”形曲线的转折点均与二产比例和工业部门终端能源消费强度的倒“U”形曲线的峰值点相对应，这表明一方面工业部门的发展对终端能源消费的依赖程度开始减缓；另一方面工业化过程中产业结构发生了重大调整，二产比例开始下降。

同时，三个类型的人均工业部门终端能源消费与人均GDP的“S”形曲线的零增长点与人均钢铁消费的“S”形曲线的零增长点和城市化率的平稳点(即增速接近零的点)相对应，说明了高耗能的钢铁等工业对能源需求开始呈现缓慢下降趋势；城市化率稳定增长，意味着国家基础设施建设基本完备，工业部门的能源消费开始呈现平稳或下降的趋势。

S4：构建“S”形数学模型：在人均工业部门终端能源消费与人均GDP的“S”形理论模型的基础上，运用趋势分析法和双曲正切数学方法构建以人均GDP为自变量的工业部门终端能源需求预测方程，即“S”形曲线趋势性拟合方程：

其中，所述步骤S4还包括如下步骤：

S41：采用趋势分析方法，构建人均工业部门终端能源消费E与人均GDP值G的非平坦式方程式：

$E-E_i=A\frac{\exp \left({\mathrm{\α}}_1\right(G-G_i))-\exp (-{\mathrm{\α}}_3(G-G_i))}{2\cosh \left({\mathrm{\α}}_2\right(G-G_i))}---\left(1\right)$

其中，α₁、α₂、α₃为指数常数，单位与G^-1相同；E_i、G_i分别为曲线在转折点对应的人均工业部门终端能源消费和人均GDP值；A为趋势关系方程(1)的振幅值，单位与G相同；

S42：由方程(1)得曲线在起飞点前、转折点临近区域、零增长点后线性变化的方程分别为：

E-E_i＝A+A(α₂-α₃)(G-G_i)＝A+ρ_l(G-G_i) (2)

E-E_i＝0.5A(α₁+α₃)(G-G_i)＝ρ_i(G-G_i) (3)

E-E_i＝A+A(α₁-α₂)(G-G_i)＝A+ρ_v(G-G_i) (4)

其中，ρ_l、ρ_i、ρ_v分别为曲线在起飞点前、转折点临近区域、零增长点后线性变化区域的斜率值，G_v为曲线在零增长点的人均GDP值；

S43：由方程(2)～(4)得α₁、α₂、α₃诸待定常数与斜率相联系的方程分别为：

${\mathrm{\α}}_1=\frac{{\mathrm{\ρ}}_1+{\mathrm{\ρ}}_i+{\mathrm{\ρ}}_v}{2A}---\left(5\right)$

${\mathrm{\α}}_2=\frac{{\mathrm{\ρ}}_1+2{\mathrm{\ρ}}_i-{\mathrm{\ρ}}_v}{2A}---\left(6\right)$

${\mathrm{\α}}_3=\frac{-{\mathrm{\ρ}}_1+2{\mathrm{\ρ}}_i-{\mathrm{\ρ}}_v}{2A}---\left(7\right)$

同时曲线在零增长点处有：

$\tanh \left({\mathrm{\α}}_1\right(G_v-G_v\left)\right)\tanh \left({\mathrm{\α}}_2\right(G_v-G_i\left)\right)={\mathrm{\α}}_1{\mathrm{\α}}_2^{-1},\frac{dE}{dG}=0---\left(8\right);$

S44：将(5)、(6)二式代入方程(8)得到：

tanh(η₁A^-1)tanh(η₂A^-1)＝η₃ (9)

其中，

η₁＝0.5(ρ_l+ρ_i+ρ_v)(G_v-G_i) (10)

η₂＝0.5(ρ_l+2ρ_i-ρ_v)(G_v-G_i) (11)

${\mathrm{\η}}_3=\frac{{\mathrm{\ρ}}_1+{\mathrm{\ρ}}_i+{\mathrm{\ρ}}_v}{{\mathrm{\ρ}}_1+2{\mathrm{\ρ}}_i-{\mathrm{\ρ}}_v}---\left(12\right);$

S45：由具体数据给出G_i、E_i、G_v、ρ_l、ρ_i、ρ_v值，代入方程(9)中计算出A值；

S46：由方程(5)～(7)式依次计算出α₁、α₂、α₃值，得出“S”形曲线趋势性拟合方程，即工业部门终端能源需求预测方程，也即方程(1)的具体形式。

S5：预测：设定预测的时间长度，根据不同国家或地区经济发展规划或增长趋势，确定预测期内的GDP和人口，计算得到人均GDP，作为自变量。

S6：将预测时点的人均GDP代入步骤S4中得到的预测方程中，求得不同国家/地区的工业部门终端能源需求预测结果。

最后通过结合国家工业部门发展趋势及“S”形理论模型中与其他重要指标间的内涵关系，对预测结果的可靠性、准确性进行评估和验证。

基于上述基于S形模型的工业部门终端能源需求预测方法，本发明同时提供一种美国的工业部门终端能源需求预测方程，其方程式为：

$E=1.68+1.63\frac{\exp \left(0.00002\right(G-11230))-\exp (-0.00018(G-11230))}{2\cosh \left(0.00024\right(G-11230))}.$

如表2所示，通过已知的人均GDP值，根据上述方程计算出美国工业部门终端能源消费拟合值，并将其与实际的工业部门终端能源消费作对比，可计算出其历史拟合值的误差率小于±10％。

表2：美国的工业部门终端能源消费需求预测方程误差结果分析

基于上述基于S形模型的工业部门终端能源需求预测方法，本发明同时提供一种加拿大的工业部门终端能源需求预测方程，其方程式为：

$E=1.76+3.5\frac{\exp \left(0.000046\right(G-11605))-\exp (-0.000051(G-11605))}{2\cosh \left(0.00019\right(G-11605))}.$

基于上述基于S形模型的工业部门终端能源需求预测方法，本发明同时提供一种英国的工业部门终端能源需求预测方程，其方程式为：

$E=0.68+1.35\frac{\exp \left(0.00002\right(G-7718))-\exp (-0.00014(G-7718))}{2\cosh \left(0.0002\right(G-7718))}.$

基于上述基于S形模型的工业部门终端能源需求预测方法，本发明同时提供一种法国的工业部门终端能源需求预测方程，其方程式为：

$E=0.61+2.5\frac{\exp \left(0.00004\right(G-6200))-\exp (-0.000\mathrm{05}(G-6200))}{2\cosh \left(0.00027\right(G-6200))}.$

基于上述基于S形模型的工业部门终端能源需求预测方法，本发明同时提供一种德国的工业部门终端能源需求预测方程，其方程式为：

$E=0.\mathrm{92}+2.7\frac{\exp \left(0.00003\right(G-\mathrm{9159}))-\exp (-0.000\mathrm{12}(G-9159))}{2\cosh \left(0.0004\right(G-9159))}.$

基于上述基于S形模型的工业部门终端能源需求预测方法，本发明同时提供一种日本的工业部门终端能源需求预测方程，其方程式为：

$E=0.77+2.3\frac{\exp \left(0.00002\right(G-\mathrm{7100}))-\exp (-0.0009(G-\mathrm{7100}))}{2\cosh \left(0.000\mathrm{16}\right(G-\mathrm{7100}))}.$

基于上述基于S形模型的工业部门终端能源需求预测方法，本发明同时提供一种意大利的工业部门终端能源需求预测方程，其方程式为：

$E=0.\mathrm{48}+1.2\frac{\exp \left(0.0000\mathrm{75}\right(G-\mathrm{7300}))-\exp (-0.000\mathrm{11}(G-\mathrm{7300}))}{2\cosh \left(0.000\mathrm{19}\right(G-\mathrm{7300}))}.$

综上，本发明提供的基于S形模型的工业部门终端能源需求预测方法，以人均工业部门终端能源消费基本规律为指导，从根本上解决了以往部门能源需求预测普遍存在的预测偏差大的问题，提高了预测可靠性和置信度。建立了一种兼具普适性和针对性的工业部门终端能源需求预测方法，预测方法实用便捷，易于实现和推广。其主要用于国家或地区中长期的工业部门终端能源需求预测，其成果可直接应用于考察国家能源消费的部门转移与能源品种的变化以及制定工业发展相关政策等领域。