一种基于粒子群算法的三角网格规范化方法与流程

本发明涉及逆向工程的实物测量数据的三角网格模型重建，具体涉及一种基于改进粒子群算法的三角网格规范化方法。
背景技术：
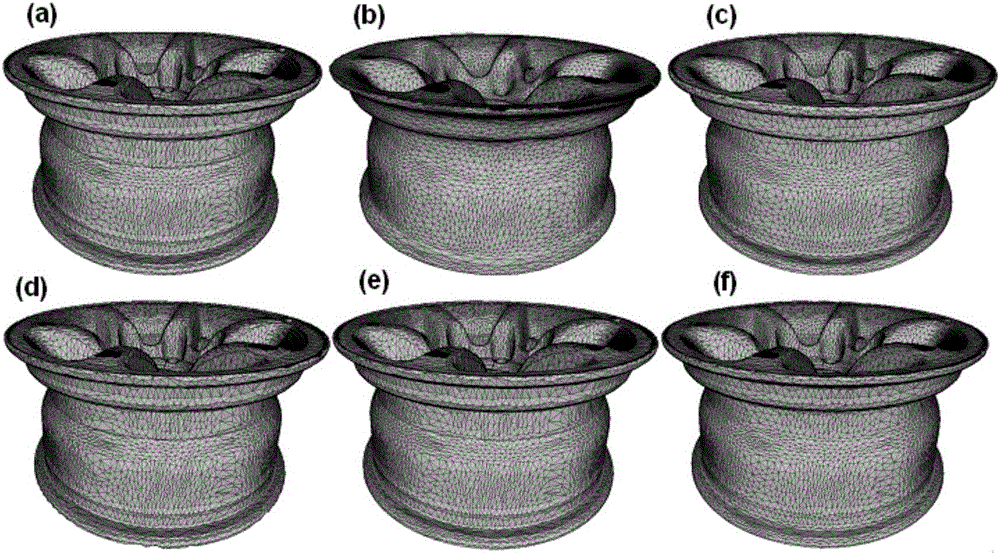
：在逆向工程中，根据实物测量数据进行三角网格模型重建是重要研究内容之一。由于实物测量数据的复杂性和网格生成算法的不足，在重建的三角网格模型中，往往存在狭长三角形、冗余三角形、不共顶点三角形以及孔洞等非规范化网格。在对实体模型进行有限元分析时，这种非规范化的网格会直接影响分析的精度和效率，甚至造成计算结果不收敛；此外，在快速原型制造(3D打印)中，这种非规范化的网格也会导致效率和稳定性降低。因此，有必要对重建的三角网格模型进行规范化处理，为后续的应用提供高质量的网格。狭长三角形规范化处理是将网格中的三角形尽可能调整成正三角形。在狭长三角形规范化处理方面，很多其他方法针对如何保持几何特征、减少体积收缩和提高算法效率等方面进行，在一定程度上改善了网格的质量。主要方法有Laplace算法，该算法的应用最广，基本思想是以一定的速率沿拉普拉斯算子的方向对顶点进行调整，该算法调整后的三角形网格质量较高，但网格模型体积和表面积会发生收缩。针对Laplace方法的不足，有学者构造低通滤波器，能够有效抑制噪声，在一定程度上抑制了模型收缩问题，但是带来了新的扰动。有方法采用保体积规范化，有效抑制模型收缩，但是得到的网格模型质量一般。还有学者提出一种结合双边滤波和图像滤波优点的组合优化算法，取得很好的网格规范化效果，但是该算法在顶点曲率的计算上误差较大。针对双边滤波方法的不足，有学者进行改进，与准拉普拉斯算子结合先对顶点位置进行预测，然后同时沿顶点的法向量方法和切平面方向对顶点位置进行调整，该方法可有效保持网格模型的几何细节特征，同时网格形状也较均匀，但是算法中需要设置较多的参数。针对上述方法的不足，本发明提出了一种新的三角形网格规范化方法。技术实现要素：本发明为解决狭长三角形规范中抑制网格体积和表面积发生收缩的同时，能够保持网格模型的几何特征和细节特征，提高网格模型中三角形质量的问题，提出一种新的三角形网格规范化方法。本发明的方法为一种基于改进粒子群算法的三角网格规范化方法：首先，使用最小二乘法将三角形每个顶点及其一阶邻域顶点拟合成一个局部三次曲面；然后，以拟合的局部曲面为粒子群算法的搜索域，以局部三角形的平均质量最优为目标，对网格顶点进行调整；最后，为保证模型的细节特征，通过判断顶点调整前后的法向夹角是否在阈值内，来确定该顶点是否需要调整。为避免陷入局部最优，并加快收敛速度，本发明对粒子群算法进行了改进：引入了粒子中心位置、约束因子以及自适应惯性因子。1)三角网格模型的局部曲面拟合虽然重建的三角网格模型是离散的，但从局部来看，可认为其是连续的。所以可把三角网格模型上的一个个局部网格看成为一个个局部曲面，网格上的点都分布在这些局部曲面上。这样，三角形的规范化处理就是将三角网格模型中三角形的顶点在局部曲面上调整的过程。本发明利用最小二乘法对网格模型中三角形的每个顶点及其一阶邻域顶点进行三次曲面拟合，并将拟合的曲面作为顶点调整的区域约束，用于避免网格模型的几何变形和体积收缩。为使用顶点Vi及其一阶邻域顶点集合N(Vi)拟合一个三次曲面，本发明以顶点Vi为原点，Vi的法向量ni为z轴的正向，建立一个局部坐标系，新坐标系下顶点Vi和N(Vi)拟合的三次曲面定义为：f(x,y)＝Ax3+By3+Cx2y+Dxy2+Ex2+Fy2+Gxy+Hx+Iy+J(1)(x，y，z)表示拟合曲面f(x,y)上任意一点的坐标，公式(1)中的f(x,y)就是坐标z。利用公式(1)对顶点Vi及N(Vi)进行局部曲面拟合；公式中的A、B、C、D、E、F、G、H、I和J均表示系数；通过求解局部曲面方程进而得到拟合曲面方程f(x,y)的系数。求解局部曲面方程式(1)系数的具体步骤如下：Step1求三次曲面函数f(x,y)的偏导数，得到f(x,y)的法向方程N(x,y)：N(x,y)＝(3Ax2+2Cxy+Dy2+2Ex+Gy+H,3By2+Cx2+2Dxy+2Fy+Gx+I,-1)(1-1)Step2局部坐标系下令每个点(xi,yi,zi)的法向量为(ai,bi,ci)，为与式(1-1)形式一致，将其改写为(-ai/ci,-bi/ci,-1)。Step3将式(1)中的各系数写成列向量的形式：x＝(ABCDEFGHIJ)T(1-2)Step4对于局部坐标系下每个点(xi,yi,zi)，列出以下等式：(xi3,yi3,xi2yi,xiyi2,xi2,yi2,xiyi,xi,yi,1)x=zi---(1-3)]]>(3xi2,0,2xiyi,yi2,2xi,0,yi,1,0,0)x=-ai/ci---(1-4)]]>(0,3yi2,xi2,2xiyi,0,2yi,xi,0,1,0)x=-bi/ci---(1-5)]]>Step5将式(1-3)、式(1-4)和式(1-5)联立成一个线性方程组：Mx＝b(1-6)式(1-6)中M是一个矩阵，维数为3n×10；b是一个列向量，维数为3n；n是N(Vi)中顶点的个数，若n＜4，则取距离顶点Vi较近的二阶邻域顶点。Step6求解式(1-6)，得到一个最小二乘意义下的可行解，即拟合曲面方程f(x,y)的系数。在本发明的规范化算法中，该拟合曲面将作为改进的粒子群优化算法的搜索区域。2)初始化粒子，将粒子的当前位置作为个体历史最优，按照公式(2)确定群体最优位置。Pgt={Pit|min{f(P1t),f(P2t),...,f(Pmt)}}---(2)]]>式中为整个种群在第t次迭代后的群体最优解；f(*)为适应度函数，m为种群规模；第i个粒子在第t次迭代时个体历史最优解，通过公式(3)得到。Pit={Xin|min{f(Xi1),f(Xi2),...,f(Xit)}}---(3)]]>粒子个体历史最优位置的选择方式通过公式(4)得到。Pit+1=Xit+1,f(Xit+1)≤f(Pit)Pit,f(Xit+1)>f(Pit)---(4)]]>公式(3)和(4)中，分别为第i个粒子在第t次迭代时的位置和第t+1次迭代时的位置；分别为第i个粒子在第t和第t+1次迭代时个体历史最优解。标准粒子群优化算法的可靠性并不理想，尤其是在高阶寻优时，容易陷入局部最优，为避免出现这种情况，本发明在标准粒子群算法中的速度迭代公式中增加一个干扰项，将当前迭代时有效粒子的中心位置作为干扰项，该干扰项表征的是大多数优秀粒子的影响力，从而将某一个优秀的粒子对粒子群整体的吸引力进行有效的分散。所以最后通过公式(5)计算粒子中心位置。Pct={Xit|Med{f(X1t),f(X2t),...,f(Xmt)}}---(5)]]>式中，为第t次迭代时粒子群的中心位置，为第i个粒子在第t次迭代时的位置，f(*)为适应度函数，Med(*)为中值滤波函数，m为种群规模。3)确定顶点Vi的搜索区域使顶点Vi的新位置坐标满足公式(6)-(10)的约束条件。Δx=max{|xi|-|x1Vi|,|xi|-|x2Vi|,...,|xi|-|xVsumVi|}---(6)]]>Δy=max{|yi|-|y1Vi|,|yi|-|y2Vi|,...,|yi|-|yVsumVi|}---(7)]]>x~i∈{xi-Δx,xi+Δx}---(8)]]>y~i∈{yi-Δy,yi+Δy}---(9)]]>z~i=f(x~i,y~i)=Ax~i3+By~i3+Cx~i2y~i+Dx~iy~i2+Ex~i2+Fy~i2+Gx~iy~i+Hx~i+Iy~i+J---(10)]]>式(6)-(10)中，为第i个顶点Vi的新位置坐标，Vsum为顶点Vi一阶邻域顶点的个数，j＝1,2,...,Vsum分别为顶点Vi一阶邻域的第j个顶点x轴和y轴的坐标值，Δx,Δy分别为顶点Vi调整时x轴和y轴坐标值的变化范围，Vsum为顶点Vi一阶邻域顶点的个数。公式(10)为根据顶点Vi及N(Vi)拟合的三次曲面方程，作为顶点Vi调整的约束条件，确保在顶点调整过程中，网格模型的几何尺寸不收缩。另外，为更好的保持网格模型的细节特征，在使用改进的粒子群算法获取顶点新位置后，再根据顶点调整前后法向量之间的夹角大小来确定该顶点是否需要移动到新位置。4)粒子位置和速度的迭代更新粒子群算法的数学描述为：在解空间中，N个粒子代表N个可能的解，粒子的运动过程就是解的搜索过程，粒子的运动速度是搜索方向，每个粒子根据自身的历史信息和群体信息综合确定自己的速度和位置，每个粒子的速度和位置迭代公式为：Vit+1=ωVit+c1r1(Pit-Xit)+c2r2(Pgt-Xit)---(11-1)]]>Xit+1=Xit+Vit+1---(12-1)]]>首先，为实时调整算法的搜索范围，本发明对粒子群算法的惯性因子ω进行改进，即公式(11-1)。惯性因子ω反映的是粒子对自身当前速度的继承程度，通过改变ω的取值，可以动态调整粒子群算法的搜索能力。当ω较大时，具有较强的全局搜索能力；当ω较小时，具有较强的局部搜索能力。本发明使用粒子适应度值与目标的误差，定义一个自适应调整的惯性因子ωa。其次，为加快粒子群算法的收敛速度，减小粒子振荡幅度，避免无效的迭代，本发明在粒子群算法的位置迭代公式中(12-1)引入一个约束因子ξ。由于本发明通过引入粒子中心位置的干扰、约束因子ξ以及自适应惯性因子ωa对粒子群算法进行改进。所以，在本发明中，对每个粒子的速度和位置按照改进后算法的速度和位置迭代公式(11)和(12)进行迭代更新。Vit+1=ωaVit+c1r1(Pit-Xit)+c2r2(Pgt-Xit)+c3r3(Pct-Xit)---(11)]]>Xit+1=Xit+ξVit+1---(12)]]>粒子的速度约束条件为：|Vit+1|≤Vmax---(13)]]>式中，为第t次迭代时粒子群的中心位置，c1、c2为学习因子，c3为中心学习因子；r1、r2和r3均服从(0，1)的随机分布；ωa为自适应调整的惯性因子；ξ为约束因子；m为种群规模，Vmax为粒子最大限制速度。ωa＝ωmin+(ωmax-ωmin)(E(x)-E(x)min)/(E(x)max-E(x)min)(14)式中，ωmin、ωmax分别为惯性因子的最小值和最大值，当ωmin＝0.4，ωmax＝0.9时，粒子群算法的收敛速度和求解精度都较高；E(x)max、E(x)min分别为迭代过程中当前所有粒子适应度与目标之间误差的最大值和最小值；E(x)为当前粒子与目标之间的误差值；由式(14)知，定义的惯性因子ωa的取值与粒子当前位置距离目标位置的远近成正比，算法运行过程中可根据该粒子的当前位置实时调整算法的全局搜索能力和局部搜索能力，从而提高算法的求解精度。式(15)中，为约束因子计算过程中的中间符号，且5)计算粒子适应度值，并更新粒子个体历史最优、群体历史最优以及粒子中心位置；将局部网格模型中三角形质量定义为算法目标函数,按照公式(16)计算每个粒子的适应度值；minQ(NVi)=1-Qave(NVi)=1-(Σk=1Tsum43Sklk12+lk22+lk32)/Tsum---(16)]]>Qave=Σk=1TsumQk/Tsum---(17)]]>Qk=43Sk/(lk12+lk22+lk32)---(18)]]>公式(16)-(18)中，式中，为适应度函数，为顶点Vi的一阶邻域三角形集合；Tsum为局部网格模型中三角形的个数，Qk为第k个三角形的质量；Sk为第k个三角形面积；lk1、lk2、lk3为第k个三角形的边长；Qk描述一个三角形的质量。然后分别按照公式(3)和(2)更新粒子的个体历史最优和群体历史最优，最后按照公式(5)重新计算粒子中心位置；6)若迭代结束或误差阈值满足条件，转到步骤7)，否则跳转到步骤3)；7)保存顶点的新位置坐标计算顶点新位置与原始位置的法向量之间的夹角并保存；8)若在阈值范围内，更新顶点位置和顶点的法向量信息，否则保持原顶点位置不变；9)若已遍历网格模型中的全部顶点，网格规范化结束，否则跳转到步骤1)。本发明的有益效果，本发明方法在抑制网格体积、表面积发生收缩以及保持网格几何特征的同时，能有效改善三角网格模型中的三角形质量。本发明通过引入粒子中心位置Pc、约束因子ξ以及自适应的惯性因子ωa对粒子群算法改进，不仅能有效避免算法运行时陷入局部最优，而且能加快算法的收敛速度、实时调整算法的搜索范围；以顶点的局部拟合曲面为粒子群的搜索域，解决了大多算法规范化后三角网格模型体积收缩的问题；通过判断顶点调整前后的法向夹角是否在阈值内，来确定该顶点是否需要调整，保证了规范化后网格模型的细节特征不丢失。附图说明图1为本发明流程图；图2为轮毂模型的规范化效果比较；图3为汽缸盖模型的规范化效果比较；图4为规范化后汽缸盖模型的局部网格形状；图2-图4中(a)原始模型，(b)拉普拉斯法的规范化效果，(c)Taubin法的规范化效果，(d)Vollmer法的规范化效果，(e)陈中方法的规范化效果，(f)本发明方法的规范化效果。具体实施方式下面结合附图和实施例对本发明作进一步说明，但不应该理解为本发明上述主题范围仅限于下述实施例。在不脱离本发明上述技术思想的情况下，根据本领域普通技术知识和惯用手段，做出各种替换和变更，均应包括在本发明的保护范围内。本发明流程图参见图1。在VisualC++6.0的环境下实现了该算法，在IntelCore2CPU2.2GHz，内存为3G的PC机上运行程序，算法中的参数设置如表1所示。为验证算法的有效性，以基于工业CT图像重建的轮毂模型和汽缸盖模型为例，与拉普拉斯方法、Taubin方法、Vollmer方法以及陈中方法等进行对比，这些方法中的参数均根据原参考文献设定。表1本发明算法参数设置因算法中粒子寻优的过程相对简单，通过实验发现迭代次数在5次左右，即能找到顶点的最佳位置，故将算法的迭代次数设为5；粒子群算法中群体规模一般取20～40，但群体规模取值越大，算法的效率越低，另外由于本实施例中拟合的局部曲面范围较小，故实验中将群体规模设为11，取奇数是为了方便获取粒子中心位置；学习因子c1、c2、c3分别反映的是粒子对自身的认知能力、粒子间的信息共享合作能力以及粒子中心的平衡能力，c1、c2取经验值2.05，为使粒子中心在算法中的影响力与粒子个体最优、群体最优相同，c3也取2.05；迭代继续的条件是前后两次迭代的结果误差大于0.01；法向量角度误差阈值越小，特征保持越好，网格的三角形质量相对就差，角度误差一般设为5°-15°，为在网格模型特征及三角形质量之间取得平衡，本实施例优选将法向量夹角阈值设为8°。实验结果参见图2、图3和图4。图2为各种算法对轮毂模型的规范化结果显示，图3为各种算法对汽缸盖模型的规范化结果显示，图4为规范化后汽缸盖模型的局部放大结果。从图2中可以看出，图2(b)中拉普拉斯算法规范化后的轮毂模型网格质量较好，但其特征有所丢失且整体有所变形；图2(c)中Taubin法和图2(d)中Vollmer法规范化的模型在一定程度上保持了特征，但网格中三角形的质量较差；图2(e)中陈中方法规范化后的模型特征保持较好，但网格中三角形的质量一般；图2(f)是本发明方法规范化后的网格模型，不仅能很好地保持轮毂模型的细小特征(如轮毂边缘处等)，而且网格中三角形的质量也较好。对图3中不同算法规范化后的汽缸盖模型分析，可以直观看出，图3(c)Taubin方法、图3(e)陈中方法、图3(f)本发明方法规范化后的模型能较好地保特征，而Laplace方法和Vollmer方法规范化后的模型边缘轮廓大幅变形。从图4不同算法规范化后模型的局部放大图中可以看出：本发明方法与Laplace方法规范化后，模型中的三角形比较均匀，质量较好，但Laplace方法的细节特征丢失较多，而其他方法规范化后，网格模型中的三角形质量较差。为更准确的对各种算法的性能进行比较，对不同算法规范化后的模型信息进行量化统计。表2为原始模型的相关信息；表3统计了不同方法规范化后网格模型的包围盒尺寸、表面积、体积，与原始模型相比不同算法下模型的最大误差，平均误差，不同算法所用的时间等；表4分别对不同方法下网格模型中三角形的质量分布进行了统计。表2原始模型的基本数据表3各种规范化方法的性能比较表4各规范化方法下模型中三角形质量分布从表3、表4中的数据可以看出，本发明方法与其他规范化方法相比，轮毂模型和汽缸盖模型的最小包围盒尺寸与原始模型的基本一致，并且模型的体积、表面积与原始模型之间的误差也较小，能较好的保持模型的几何特征；最重要的是本发明方法规范化后网格模型中狭长三角形的数量急剧减少，三角形的质量最高，大大提高了模型中三角形的规范化程度。但本发明方法由于需要先对每个顶点的一阶邻域顶点进行局部曲面拟合，再进行顶点寻优，所以算法运行时间相对较长。当前第1页1 2 3