基于应力‑强度干涉理论的高超声速飞行器翼梁结构可靠性分析方法与流程

本发明属于结构安全可靠性
技术领域：
，涉及一种高超声速飞行器机翼翼梁结构强度的可靠性分析方法。
背景技术：
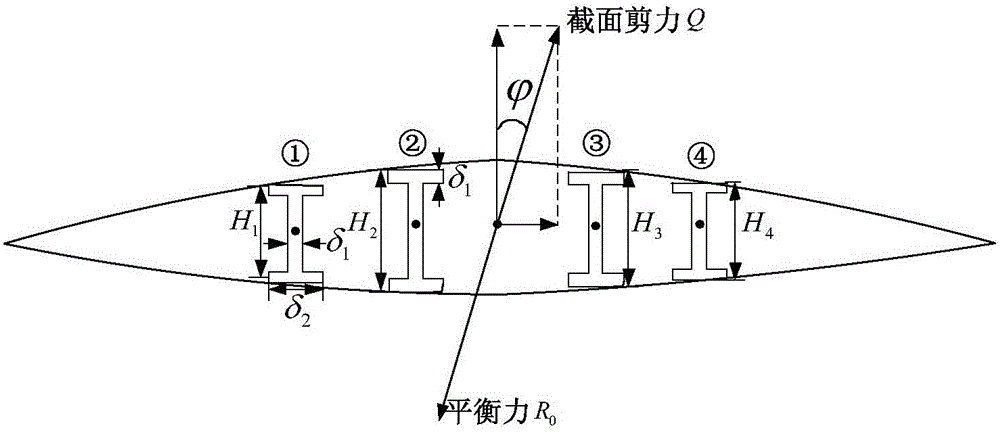
：机翼作为飞行器上最重要的部件之一，其主要功能是产生升力和控制飞行器飞行姿态。高超声速飞行器在执行任务过程中飞行速度遍历亚声速、跨音速、超声速以及高超声速，飞行高度跨越连续流区、过渡流区和稀薄流区，在飞行过程随着马赫数的不断增加以及迎角不断变化，飞行器与周围大气相互作用，产生复杂的气动干扰现象，从而使得机翼表面气动载荷分布、压心和力矩受到很大的影响。机翼翼梁根部不仅需要承受飞行器自身的重力，还要承受机翼在超高速气流中受到的巨大的气动载荷所带来的应力作用。因此机翼翼梁根部作为机翼的关键部件出现疲劳破坏的概率是最大的，其对于飞行器飞行安全的影响也是最大的。在航空航天领域，目前的结构可靠性研究主要针对火箭及飞行器发动机部件，飞行器螺旋桨叶片、起落架结构等，对飞行器机翼可靠性分析的研究较少，而对于高超声速飞行器机翼可靠性的研究，目前还没有见到相关的研究文献。并且，在已有的可靠度分析的研究中，绝大多数都是针对静态应力对结构可靠度的影响，并没有考虑载荷循环次数以及结构强度退化对可靠性的影响，比如论文《航空发动机叶片疲劳寿命和可靠性研究》、《基于矩方法的无人机机翼可靠性分析》以及《飞机翼梁结构强度可靠性灵敏度分析》。而在实际的飞行过程中，机翼所承受的载荷绝大多数都是动态随机循环载荷，并且材料自身存在一定的疲劳寿命，因此在分析机翼结构可靠度时考虑载荷循环次数以及结构强度退化将更加符合实际的情况。本发明基于应力-强度干涉理论建立了机翼结构强度可靠性分析模型与失效率模型。应力-强度干涉模型优势在于模型相对简单，可以有效利用疲劳载荷统计数据以及材料强度数据，在考虑载荷作用次数、载荷大小以及增加试验数据量的情况下，仍具有较高精度。技术实现要素：本发明为了克服现有技术的不足之处，提供一种基于应力-强度干涉理论的高超声速飞行器机翼翼梁结构强度可靠性分析方法，在分析机翼结构可靠度时考虑了随机载荷循环次数以及结构强度退化的影响，使得分析结果更加符合实际情况。本发明采用以下技术方案：一种基于应力-强度干涉理论的高超声速飞行器机翼翼梁结构强度可靠性分析方法，包括如下步骤：步骤1)，选取翼型为薄对称菱形、翼梁为壁梁结构、翼梁数量为四根的机翼作为高超声速飞行器机翼受力分析参考模型；步骤2)，分析翼面受力分布，建立翼梁根部的受力分析模型，计算翼梁根部的拉应力、压应力与剪切应力；步骤3)，将飞行器飞行包线均匀划分为三个阶段，分别是：爬升段、巡航段、下降段，在各个飞行阶段中依次选取包含不同高度、不同空速、不同迎角以及不同舵面偏角的几种飞行状态，计算机翼翼梁根部在不同飞行状态下的应力载荷，并求取相当应力作为可靠度参考应力；步骤4)，根据步骤3)中求取的机翼翼梁根部在不同飞行状态下的应力载荷情况，结合翼梁根部在特定温度下的强度，并考虑在飞行过程中的随机载荷次数以及强度随飞行次数增加而退化的情况，基于应力-强度干涉理论建立可靠度分析模型与失效率模型。在上述的各步骤中，所述步骤2)中建立的翼梁根部受力分析模型如下：σ1=M1Hm8IZ1]]>σ2=M3δ28IZ2]]>上式中，σ1和σ2为在弯曲力矩M1以及弯曲力矩M3作用下翼梁根部受到的平均拉-压应力，Hm为高度分别为H1、H2、H3、H4的四根翼梁的平均高度，IZ1和IZ2为弯曲力矩M1以及弯曲力矩M3作用下翼梁截面惯性矩，有如下形式：IZ1=δ2Hm3-δ1(Hm-2δ1)312]]>IZ2=Hmδ23+(Hm-2δ1)δ1312]]>其中δ1为翼梁腹板厚度以及缘条厚度，δ2为缘条宽度。忽略机翼气动焦点到机翼重心的距离，弯曲力矩M1、M3形式如下：M1＝[(L-Mwg)cosα+Dsinα]lM3＝[Dcosα-(L-Mwg)sinα]lτQ1、τQ2为在升力L与阻力D作用下翼梁根部所受纵向切应力和横向切应力，其平均大小分别为：其中表示截面剪力Q与翼面法线间的夹角，A1～A4分别为四根翼梁的截面面积，有：Ai＝Hiδ2-(δ2-δ1)(Hi-2δ1)i＝1,2,3,4式中Hi为对应编号翼梁的高度。作用于翼梁根部的截面剪力Q由M1的反作用矩M2产生，其平衡力为R0，有：|Q|=|R0|=|F|=(L-Mwg)2+D2]]>所述步骤3)中求取机翼翼梁根部所受相当应力的方法如下：σ＝σ1+σ2τ=τQ12+τQ22]]>其中σ与τ分别为拉-压应力σ1、σ2的合力以及剪切应力τQ1、τQ2的合力。将多个应力作用对材料的损伤等效为一个单向应力作用对材料的损伤，该单向应力可称为相当应力，用σE表示。所述步骤4)中考虑在飞行过程中的随机载荷次数以及强度随飞行次数增加而下降的情况，基于应力-强度干涉理论建立可靠度分析模型与失效率模型，包括以下步骤：步骤4-1)，定义机翼翼梁结构可靠度为翼梁的结构强度r大于所受应力s的概率，即r＞s的概率。机翼结构强度r与应力载荷s均服从截尾正态分布，其概率密度函数分别为：fr(r)=1arσr2πexp[-(r-μr)22σr2]]]>fs(s)=1asσs2πexp[-(s-μs)22σs2]]]>其中，μr，σr分别是材料0.2％屈服强度σ0.2的均值与标准差，μs、σs分别是整个飞行过程中翼梁根部所受相当应力σE的均值和标准差；分别为正规化常数。步骤4-2)，假设飞行器前t次飞行中机翼共受到n次气动载荷，每次气动载荷过程相互独立，当强度的概率密度函数fr(r)已知，并考虑强度退化时，由应力-强度干涉理论可得到载荷作用n次时结构可靠度表达式如下：R*[r(t)]=∫0σultfr(r){Fs[r(t)]}ndr]]>其中，积分上限可选取材料在常温下的极限拉伸强度σult，Fs[r(t)]为考虑了强度退化的应力载荷分布函数，形式如下：Fs[r(t)]=∫0r(t)fs(s)ds]]>其中积分上限r(t)为结构在第t次飞行时的剩余强度，其可表示为结构初始强度r0与飞行次数t的函数。步骤4-3)，在每次飞行周期内机翼受到的气动载荷作用次数l均服从截尾正态分布，其概率密度函数为：fl(l)=1alσl2πexp[-(l-μl)22σl2]]]>其中μl、σl为每次飞行中机翼受到载荷次数的均值和标准差，其具体数值由实际测试所得的载荷统计数据得到，al为正规化常数。当飞行器飞行总次数为t时，在这t次飞行中机翼受到载荷总次数N服从一维截尾正态随机过程，其概率密度函数可表示为：fN(N,t)=1aN(t)σN(t)2πexp{-[N-μN(t)]22σN(t)2}]]>其中μN(t)、σN(t)、aN(t)分别为载荷总次数N的均值、标准差以及正规化常数。步骤4-4)，飞行器在t次飞行中机翼受到载荷总次数N＝n的概率为：P[N(t)-N(0)＝n]＝fN(n,t)其中N(t)为0～t次飞行中机翼受到载荷的总次数，同时有N(0)＝0。由全概率公式可以得到在考虑结构强度退化的第t次飞行中机翼关键部件可靠度的表达式为：R(t)=Σn=1m(t)P[N(t)-N(0)=n]R*[r(t)]=Σn=1m(t)fN(n,t)R*[r(t)]=Σn=1m(t)1aN(t)σN(t)2πexp{-[n-μN(t)]22σN(t)2}∫0σultfr(r){Fs[r(t)]}ndr]]>其中函数m(t)表示t次飞行中机翼受到载荷总次数n的最大可能值，有如下形式：m(t)＝kμN(t)式中m(t)取值范围由参数k控制。定义失效率为机翼翼梁根部在t～t+1次飞行中可靠度下降比率，则可以得到其失效率模型如下：F(t)=R(t)-R(t+1)R(t)=1-R(t+1)R(t)=1-Σn=1m(t)fN(n,t+1)R*[r(t+1)]Σn=1m(t)fN(n,t)R*[r(t)]]]>本发明采用上述技术方案，具有如下有益效果：1、通过对高超声速飞行器机翼翼梁根部在气动升力与气动阻力的作用下受到的拉-压应力与剪切应力进行分析，提供了一种机翼翼梁根部受力分析的方案，拟补了现有资料在高超声速飞行器机翼翼梁受力分析方面的欠缺；2、建立了在随机循环载荷作用下，并考虑结构强度随飞行次数增加而退化的情况下高超声速飞行器机翼翼梁根部的可靠度模型以及失效率模型，相比于已有的基于静态力作用下的可靠度模型或者假设强度恒定情况下的可靠度模型，本发明中提出的可靠度模型拥有更高的精度，也更加符合实际情况。通过参照高超声速飞行器疲劳损伤容限设计的方法，可以确定保证飞行器飞行安全的临界可靠度，在保留一定安全余量的情况下确定飞行器的维修周期，估计飞行器的使用寿命。附图说明图1是本发明中机翼受力分析示意图；图2是本发明中机翼截面剪力示意图；图3是本发明中结构可靠度随飞行次数变化曲线示意图；图4是本发明中结构失效率随飞行次数变化曲线。具体实施方式下面结合附图及附表对本发明的作更进一步说明。由于高超声速飞行器具有十分复杂的气动特性，机翼结构也比较复杂，因此对机翼作受力分析时通常将机翼简化为壁梁结构，对其关键部件的受力分析主要是针对翼梁根部所受拉压应力和剪切应力进行分析。为了保证较好的波阻特性，高超声速飞行器机翼通常采用薄对称菱形翼型。由图1所示，机翼所受升力沿翼展方向近似按椭圆分布，机翼迎角为α。在考虑机翼自重的情况下，由升力L与波阻D垂直于翼面的合力产生一个弯曲力矩M1。M1主要作用在翼梁上，并在四根翼梁根部分别产生拉、压应力，其合力分别为P1和P1'，并对应产生一个反作用矩M2。整个翼面的气动合力F位于压力中心线上的气动焦点O点处，该合力使得翼根截面处产生一个大小相等，方向相同的剪力Q，同时产生一个大小相等，方向相反的平衡力R0。设4根翼梁的高度分别为H1、H2、H3、H4，在弯曲力矩M1作用下翼梁根部受到的平均拉-压应力为：σ1=M1Hm8IZ1---(1)]]>其中，Hm为翼梁平均高度，IZ1为翼梁截面惯性矩，可表示为：IZ1=δ2Hm3-δ1(Hm-2δ1)312---(2)]]>其中δ1为翼梁腹板厚度以及缘条厚度，δ2为缘条宽度，如图2所示。假设机翼气动焦点O到机翼重心的距离可以忽略，则弯曲力矩M1可表示为：M1＝[(L-Mwg)cosα+Dsinα]l(3)其中l为气动焦点O点沿压力中心线到翼根的距离，Mw为机翼自重，g为重力加速度。类似地，弯曲力矩M3由垂直于翼面的合力产生，在弯曲力矩M3作用下翼梁根部受到的平均拉-压应力σ2为可表示为：σ2=M3δ28IZ2---(4)]]>其中截面惯性矩与弯曲力矩有如下形式：IZ2=Hmδ23+(Hm-2δ1)δ1312---(5)]]>M3＝[Dcosα-(L-Mwg)sinα]l(6)作用于翼梁根部的截面剪力Q由M1的反作用矩M2产生，其平衡力为R0，有：|Q|=|R0|=|F|=(L-Mwg)2+D2---(7)]]>τQ1、τQ2为翼梁根部所受纵向切应力和横向切应力，平均大小分别为：其中表示截面剪力Q与翼面法线间的夹角，A1～A4分别为四根翼梁的截面面积，有：Ai＝Hiδ2-(δ2-δ1)(Hi-2δ1)i＝1,2,3,4(11)式中Hi为对应编号翼梁的高度。以上各式中，机翼升力L和激波阻力D分别为：L=12ρV2SwCL---(12)]]>D=12ρV2SwCD---(13)]]>其中，ρ为相应高度大气密度，本文参考标准大气模型USSA76来计算大气密度，V为飞行速度，Sw为单机翼面积；CL、CD分别为机翼升力系数和机翼激波阻力系数，其均可表示为迎角、马赫数以及气动舵面的函数，本文中采用的气动系数函数由高超声速飞行器实际飞行试验所测数据拟合而得。能够承受高超声速飞行所带来的高压、高温的结构材料是高超声速飞行器结构的基础。近年来各国都在开展针对高超声速飞行器结构材料以及热防护材料的相关研究，在实际飞行试验中机翼主体承力结构所采用的材料为Haynes230合金(镍基合金)。图1、图2所示的高超声速飞行器机翼结构的各几何参数如表1所示。表1在分析飞行过程中机翼翼梁根部受力载荷情况时，将整个飞行过程分为不同的三个阶段，分别是：爬升段、巡航段以及下降段，假设每次飞行总时长相同，每个阶段的历时也相同，并根据已有试验的飞行包线数据在各个阶段设计约束条件。根据约束条件，结合实际飞行试验所得到的各气动系数，可以计算出高超声速飞行器在一次飞行任务中的各个飞行阶段机翼翼梁根部所受拉压应力与剪切应力及其合力情况，其合力与各分应力的关系分别为：σ＝σ1+σ2(14)τ=τQ12+τQ22---(15)]]>根据材料力学的相关知识，可将多个应力作用对材料的损伤等效为一个单向应力作用对材料的损伤，该单向应力可称为相当应力，由结构第三强度理论得到的相当应力σE的计算公式如下：σE=σ2+4τ2---(16)]]>根据实际测试给出的飞行包线数据，在同一次飞行的各个飞行阶段中依次选取包含不同高度、不同空速、不同迎角以及不同舵面偏角的几种飞行状态，并对机翼翼梁根部在这几种飞行状态下的应力载荷进行采样计算，结果如表2-表4所示。表2所列为飞行器在爬升阶段翼梁根部应力载荷。表2(单位：Mpa)表3所列为飞行器在巡航阶段翼梁根部应力载荷。表3(单位：Mpa)表4所列为飞行器在下降阶段翼梁根部应力载荷。表4(单位：Mpa)考虑在飞行过程中的随机载荷次数以及强度随飞行次数增加而下降的情况，基于应力-强度干涉理论建立可靠度分析模型与失效率模型，包括以下步骤：步骤1、定义机翼翼梁结构可靠度为翼梁的结构强度r大于所受应力s的概率，即r＞s的概率。由结构疲劳特性可知机翼结构强度r与应力载荷s均服从截尾正态分布，其概率密度函数分别为：fr(r)=1arσr2πexp[-(r-μr)22σr2]---(17)]]>fs(s)=1asσs2πexp[-(s-μs)22σs2]---(18)]]>其中，μr，σr分别是材料0.2％屈服强度σ0.2的均值与标准差，μs、σs分别是整个飞行过程中翼梁根部所受相当应力σE的均值和标准差；分别为正规化常数，它们保证了及步骤2、考虑到机翼关键部件结构材料的强度随飞行次数的增加会存在一定程度的退化，根据合金材料结构强度疲劳退化的特性，若考虑结构强度退化形式为对数退化形式，则在第t次飞行时结构的剩余强度模型可表示为：r(t)＝r0+λln(1-α't)(19)其中，α'为材料强度退化系数，t表示飞行器按照规定约束条件完成飞行任务的飞行次数，r0为机翼翼梁根部的初始强度，其值服从密度函数为fr(r)的概率分布，λ为载荷作用过程参数，有如下形式：λ=r0-μslnNf---(20)]]>上式中参数Nf为结构在一定程度的应力载荷作用下达到某种规定的损伤状态时的最大载荷循环次数，也称为临界寿命。步骤3、假设飞行器前t次飞行中机翼共受到n次气动载荷，每次气动载荷过程相互独立，则可将n次气动载荷对翼梁根部的作用等价为等效载荷X对翼梁根部的作用，其累积分布函数与概率密度函数分别为：FX(x)=[Fs(x)]n=∫0xfX(s)ds---(21)]]>fX(s)＝n[Fs(x)]n-1fs(s)(22)上式中表示应力载荷s在(0,x)区间内的累积分布函数。当强度的概率密度函数fr(r)已知，并考虑强度退化时，由应力-强度干涉理论可得到载荷作用n次时结构可靠度表达式如下：R*[r(t)]=∫0σultfr(r)∫0r(t)fX(s)dsdr=∫0σultfr(r)FX[r(t)]dr=∫0σultfr(r){Fs[r(t)]}ndr---(23)]]>其中，积分上限可选取材料在常温下的极限拉伸强度σult，Fs[r(t)]为考虑了强度退化的应力载荷分布函数，其积分上限为结构在第t次飞行时的剩余强度r(t)，形式如下：Fs[r(t)]=∫0r(t)fs(s)ds---(24)]]>步骤4、在实际飞行过程中，飞行器容易受到一些不确定因素的干扰，使得机翼受到的气动载荷在各个采样时刻之间存在一定的随机变化。由结构随机载荷特性可知在每次飞行周期内机翼受到的气动载荷作用次数l均服从截尾正态分布，其概率密度函数为：fl(l)=1alσl2πexp[-(l-μl)22σl2]---(25)]]>其中μl、σl为每次飞行中机翼受到载荷次数的均值和标准差，为正规化常数。由概率论与随机过程相关知识可得，当飞行器飞行总次数为t时，在这t次飞行中机翼受到载荷总次数N服从一维截尾正态随机过程，其概率密度函数可表示为：fN(N,t)=1aN(t)σN(t)2πexp{-[N-μN(t)]22σN(t)2}---(26)]]>其中μN(t)、σN(t)、aN(t)分别为载荷总次数N的均值、标准差以及正规化常数，其表达式如下：μN(t)＝μlt(27)σN(t)＝σlt(28)aN(t)=Φ[μN(t)σN(t)]=Φ(μlσl)---(29)]]>步骤5、飞行器在t次飞行中机翼受到载荷总次数N＝n的概率为：P[N(t)-N(0)＝n]＝fN(n,t)(30)其中N(t)为0～t次飞行中机翼受到载荷的总次数，同时有N(0)＝0。根据应力-强度干涉模型的结构可靠性分析方法，由全概率公式可以得到在考虑结构强度退化的第t次飞行中机翼关键部件动态可靠度的表达式为：R(t)=Σn=1m(t)P[N(t)-N(0)=n]R*[r(t)]=Σn=1m(t)fN(n,t)R*[r(t)]=Σn=1m(t)1aN(t)σN(t)2πexp{-[n-μN(t)]22σN(t)2}∫0σultfr(r){Fs[r(t)]}ndr---(31)]]>式(31)即为在随机载荷作用下考虑强度退化时机翼关键部件的可靠度模型，其中函数m(t)表示t次飞行中机翼受到载荷总次数n的最大可能值，有如下形式：m(t)＝kμN(t)(32)式中m(t)取值范围由参数k控制。为了确定参数k的取值，此处引入变异系数由统计学知识可知当k＝3.667VN+1时，可使得密度函数fN(n,t)在[1,m(t)]区间内的累积分布函数值近似为1，即其意义在于，在[1,m(t)]区间内载荷总次数n的取值包括了t次飞行中机翼受到的所有可能出现的载荷次数值。进一步，定义失效率为机翼翼梁根部在t～t+1次飞行中可靠度下降比率，则可以得到其失效率模型如下：F(t)=R(t)-R(t+1)R(t)=1-R(t+1)R(t)=1-Σn=1m(t)fN(n,t+1)R*[r(t+1)]Σn=1m(t)fN(n,t)R*[r(t)]---(33)]]>本发明在Matlab2012a环境下对可靠度模型以及失效率模型进行了仿真验证实验，具体如下：1、设置飞行各阶段的约束条件如下：(1)爬升段约束条件攻角约束：4°≤α≤10°爬升高度约束：10km≤H≤35km速度约束：1Ma≤V≤10Ma升降舵偏转角度约束：10°≤δe≤20°副翼偏转角度约束：0°(2)巡航段约束条件攻角约束：α＝4°±2°巡航高度约束：H＝35km±1.5km速度约束：8Ma≤V≤10Ma升降舵偏转角度约束：0°副翼偏转角度约束：-20°≤δa≤20°(3)下降段约束条件攻角约束：-4°≤α≤-8°下降高度约束：10km≤H≤35km速度约束：1Ma≤V≤10Ma升降舵偏转角度约束：-10°≤δe≤-20°副翼偏转角度约束：0°2、由近年来的高超声速飞行器实际试验数据可知，每次飞行包含了爬升、巡航以及下降三个阶段，测试时间在650～700s范围内，在每次飞行过程中机翼受到的载荷总次数l近似服从均值μl＝1330次、标准差σl＝67次的截尾正态分布。3、基于表2-表4中的受力数据，可以计算出整个飞行过程中翼梁根部每次受到的载荷值服从μs＝112.51Mpa、σs＝44.21Mpa的截尾正态分布。同时，由Haynes230合金铸件强度特性参数可得在700℃以内材料0.2％屈服强度σ0.2服从μr＝283.51Mpa、σr＝61.02Mpa的截尾正态分布，材料的极限强度σult＝520Mpa。4、由于在800℃内材料的0.2％屈服强度σ0.2较稳定，因此可选取450℃时Haynes230合金的强度退化试验数据进行分析。若规定材料剩余强度为初始强度的90％时材料即达到其临界寿命，则在应力水平为μs≈112Mpa的循环应力作用下材料的临界寿命Nf≈138000次，进而可以得到材料退化系数结果说明：1、图3所示为翼梁根部可靠度随着飞行次数增加而逐渐降低的情况，可以看出随着飞行次数的增加，可靠度下降的趋势越来越快。同时，图3中包含了考虑强度退化和强度不退化两种情况，可以看出，在考虑结构强度退化的情况下，可靠度的下降趋势更加明显；2、图4所示为翼梁根部结构失效率随着飞行次数增加而逐渐增大的情况，可以看出随着飞行次数的增加，结构失效率的趋势越来越快。同时，图4中同样包含了考虑强度退化和强度不退化两种情况，可以看出，在考虑结构强度退化的情况下，结构失效率增大趋势更加明显；3、表5给出了考虑强度退化时高超声速飞行器模拟执行飞行任务次数t≤100次时机翼关键部件结构可靠度数据。在计算过程中，每10次求取一次可靠度均值，以便于确定满足安全飞行要求的可靠度所对应的飞行次数范围。从表中的可靠度均值计算结果可以看出，当模拟飞行次数超过30次之后，机翼关键部件的可靠度随着飞行次数增加而下降的趋势开始越来越明显，通过参照高超声速飞行器疲劳损伤容限设计的方法，可以确定保证飞行器飞行安全的临界可靠度，在保留一定安全余量的情况下确定飞行器的维修周期，估计飞行器的使用寿命。例如当保证飞行器飞行安全时的翼梁可靠度要求为99.99％，则可以估计在翼梁无检修情况下飞行器的允许使用次数约为5次。表5应当指出，对于本
技术领域：
的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。本实施例中未明确的各组成部分均可用现有技术加以实现。当前第1页1 2 3