基于变电站测试数据计算谐波阻抗和负荷谐波模型的方法与流程

本发明涉及电力系统分析与计算技术领域，是一种基于变电站测试数据计算谐波阻抗和负荷谐波模型的方法。

背景技术：

在社会各个行业中电能的应用无处不在，电能生产和运输管理显得尤为重要。现有电网中包含有各种动态和静态元件，形成了一个巨大的电力系统数学网络，其结构复杂、阶数高、强非线性、计算量巨大。为了拓展整个电力潮流的管理水平，建立基波之外的潮流模型描述是必不可少的步骤。目前，电力系统潮流网络图模型多是以下三种方式得到：1、采用典型参数，该种情况主要适用于动态元件的规划期；2、设备厂家提供的参数，该种情况适用于静态元件：线路、变压器等参数；3、实测模型参数，该种情况主要适用于励磁、PSS等动态元件。目前，还没有一种利于实测的电能质量数据以建立简化模型的方式能够完成系统谐波网架的搭建。

技术实现要素：

本发明提供了一种基于变电站测试数据计算谐波阻抗和负荷谐波模型的方法，克服了上述现有技术之不足，其能有效解决电网中的动态和静态元件形成的电网系统数学网络结构复杂、阶数高、强非线性、计算量巨大不易建立简化模型的问题以及建立电网模型系统操作步骤繁杂，可靠性低，技术风险高的问题。

本发明的技术方案是通过以下措施来实现的：一种基于变电站测试数据计算谐波阻抗和负荷谐波模型的方法，包括以下步骤：

第一步：收集变压器高压侧和低压侧的谐波数据，将关注时间段内的变压器实测历史数据导出得到谐波数据文件；

第二步：建立变压器模型，根据谐波数据文件建立变压器模型；

第三步：建立电网模型，利用叠加定理根据谐波数据文件和变压器模型建立关于谐波源和负荷的模型；

第四步：建立简化数学框架模型，将电网谐波网络简化为电网谐波阻抗模型、变压器模型和负荷谐波模型三部分；

第五步：根据输入量的概率分布和电网模型，求解得到电网谐波参数和负荷谐波参数；

第六步：根据电网谐波参数和负荷谐波参数并依据概率分布特性，计算得到电网谐波参数的特征量和负荷谐波参数的特征量；

第七步：建立谐波阻抗模型和负荷谐波模型并对谐波阻抗模型和负荷谐波模型仿真验证。

下面是对上述发明技术方案的进一步优化或/和改进：

上述第一步中可通过电能质量在线检测平台或便携式电能质量分析仪测得的实际数据推导得到谐波数据文件。

上述第三步中，建立电网模型时要收集并计算电网谐波和谐波负荷的数据，即配电线路的数据，线路、导线、配变设备、电缆和分段线路的基础数据。

上述第四步中，建立简化数学框架模型通过simulink软件来搭建电网谐波阻抗模型和负荷谐波模型简图。

上述第七步中，通过MATLAB软件对谐波阻抗模型和负荷谐波模型进行仿真验证。

本发明基于实测电能质量数据，综合二端口模型、线性叠加定律、概率统计规律理论，采用建立简化模型的方式，完成谐波阻抗和负荷谐波阻抗的求解，并完成系统谐波网架的搭建，为电力系统谐波分布和扩散提供理论依据。相比于传统的基于无功补偿支路或者注入谐波电流的方法进行谐波阻抗估计，节省了系统操作的步骤，提供模型估计技术可靠性，降低了对应的操作技术风险，本发明更加有利于电网运行和生产部门对电网网架主体结构和用户模型的分析和管理，准确分析和评估电网网架的谐波分布和流向。

附图说明

附图1为本发明实施例1的整体结构框图。

附图2为本发明实施例2的简化电网模型图。

附图3为本发明实施例2的变压器谐波模型图。

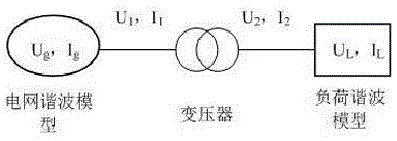
附图4为本发明实施例2的带有二端口模型的系统简化模型图。

具体实施方式

本发明不受下述实施例的限制，可根据本发明的技术方案与实际情况来确定具体的实施方式。

在本发明中，为了便于描述，各部件的相对位置关系的描述均是根据说明书附图1的布图方式来进行描述的，如：前、后、上、下、左、右等的位置关系是依据说明书附图的布图方向来确定的。

下面结合实施例及附图对本发明作进一步描述：

实施例1：如附图1所示，该基于变电站测试数据计算谐波阻抗和负荷谐波模型的方法包括以下步骤：

第一步：收集变压器高压侧和低压侧的谐波数据，将关注时间段内的变压器实测历史数据导出得到谐波数据文件；

第二步：建立变压器模型，根据谐波数据文件建立变压器模型；

第三步：建立电网模型，利用叠加定理根据谐波数据文件和变压器模型建立关于谐波源和负荷的模型；

第四步：建立简化数学框架模型，将电网谐波网络简化为电网谐波阻抗模型、变压器模型和负荷谐波模型三部分；

第五步：根据输入量的概率分布和电网模型，求解得到电网谐波参数和负荷谐波参数；

第六步：根据电网谐波参数和负荷谐波参数并依据概率分布特性，计算得到电网谐波参数的特征量和负荷谐波参数的特征量；

第七步：建立谐波阻抗模型和负荷谐波模型并对谐波阻抗模型和负荷谐波模型仿真验证。

这里，第四步中电网谐波网络为电网模型；根据需要，将电网模型进行简化，能够更直观简单的对变电站数据进行计算。

可根据实际需要，对上述基于变电站测试数据计算谐波阻抗和负荷谐波模型的方法作进一步优化或/和改进：

如附图1所示，所述的第一步中，通过电能质量在线检测平台或便携式电能质量分析仪测得的实际数据推导得到谐波数据文件。实际工作过程中可以将关注时间段内测的数据导出并以vdf或者pqdif格式的数据文件进行存储；

如附图1所示，所述的第三步中，建立电网模型时要收集并计算电网谐波和谐波负荷的数据，即配电线路的数据，线路、导线、配变设备、电缆和分段线路的基础数据。实际工作过程中，在建立电网模型之前要考虑到电网背景谐波和谐波负荷对电网模型的影响。

如附图1所示，所述的第四步中，建立简化数学框架模型时通过simulink软件来搭建电网谐波阻抗模型和负荷谐波模型简图。

如附图1所示，所述的第七步中，通过MATLAB软件对谐波阻抗模型和负荷谐波模型进行仿真验证。

实施例2：如图2、3、4所示，一种基于变电站测试数据计算谐波阻抗和负荷谐波模型的方法，包括以下步骤：

第一步：建立简化电网模型，包括变压器模型、电网谐波阻抗模型、负荷谐波模型。电网侧简化为谐波源模型，对于电流型负荷，负荷侧简化为电流源模型；对于电压型负荷，负荷侧简化为电压源模型。这里推导是电流源型模型；

第二步：建立变压器模型，根据二端口模型，简化计算公式如下：

其中：U₁、I₁为变压器一次侧电压和电流，U₂、I₂为变压器二次侧电压和电流。Y＝1/Z(h)。变压器为无源网络，阻抗矩阵具有对称特性，所以z₁₂＝z₂₁；

第三步：.求解变压器参数，变压器参数通过式(1)得到，计算公式如下：

Yy=

（3）；

第四步：变压器侧测量数据的概率分布,假设U1和I1符合高斯分布，且相互独立；则根据式(1)可以得出：

其中：Z1和Z2是U1和I1标准化之后的相互独立的标准正态分布。

根据式(4)可得出U1和I1、U2、I2符合四元联合高斯分布，对应得分布函数为：

其中∑_X为方差矩阵，(X-μ)是均值向量；

第五步：利用叠加原理，根据附图3可以得到待求变量和测量变量之间的代数关系为：

第六步：求解电网谐波阻抗模型和负荷谐波模型的概率密度,根据概率密度函数的性质，列出Ug、Zg、ZL、IL关于U1、I1、U2、I2的雅克比矩阵为：

根据式(10),Ug、Zg、ZL、IL的联合概率密度函数为：

f(U_g,Z_g,Z_L,I_L)＝f(U₁,I₁,U₂,I₂)|J|^-1；

(11)

第七步：电网谐波阻抗模型和负荷谐波模型的概率特征值求解,根据式(11)可以求解得出Ug、Zg、ZL、IL的边缘概率密度函数：

f(U_g)＝∫∫∫_R3f(U_g,Z_g,Z_L,I_L)dZ_gdZ_LdI_L

(12)

f(Z_g)＝∫∫∫_R3f(U_g,Z_g,Z_L,I_L)dU_gdZ_LdI_L

(13)

f(Z_L)＝∫∫∫_R3f(U_g,Z_g,Z_L,I_L)dU_gdZ_gdI_L

(14)

f(I_L)＝∫∫∫_R3f(U_g,Z_g,Z_L,I_L)dU_gdZ_gdZ_L

(15)

根据式(12)-(15)可以得出Ug、Zg、ZL、IL的期望和方差、95％概率值：

其他三个变量的统计特征量求解方法与公式(16)、(17)相同，这里不再赘述。

如附图2、3、4所示，在第四步中，变压器测试数据的概率分布确定有多种方法，可以用贝叶斯估计或者直接假设符合某种分布，调用统计软件函数判断是否符合某种特定的概率分布。这里举例为为高斯分布，仅为说明该方法的实现步骤，并不代表变压器的测试数据倾向于高斯分布。

以上技术特征构成了本发明的实施例，其具有较强的适应性和实施效果，可根据实际需要增减非必要的技术特征，来满足不同情况的需求。