波浪能发电系统最大输出有功功率的捕获方法及装置与流程

本发明涉及波浪能发电领域，更具体地，涉及波浪能发电系统最大输出有功功率的捕获方法及装置。

背景技术：

能源需求的不断增长和日益严峻的环境问题使人们的目光从传统能源转移到清洁可再生能源上。相对于风能、太阳能等清洁可再生能源随天气变化存在较大随机性的缺点，波浪能因单位小时内变化幅度小、能量密度高且可预测性好的优点备受青睐，如何最大限度的捕获波浪能成为波浪能发电的研究重点。

波浪能发电系统具有自身的自然频率，当波浪频率与波浪能发电系统的频率相匹配时两者发生共振，此时波浪能发电系统可以从波浪中吸取最大能量，也就是说此时波浪能发电系统获得最大输出有功功率。改变波浪能发电系统运动的幅值和相位可以改变波浪能发电系统的频率，而波浪能发电系统运动的幅值和相位受到发电机的反电磁力的影响，通过把发电机的反电磁力类比成电路中的电压，可以将反电磁力转化为一个等效阻抗与波浪能发电系统位移的微分的乘积，也就是说最佳等效阻抗的获取是提高波浪能捕获效率的关键。

现有技术对波浪能发电系统进行时域分析，在计算最佳等效阻抗时需要波浪能发电系统在海面上运行时的参数，如辐射力阻尼、当前浮子的弹簧系数等，而这些参数是会随着海面上的条件变化而变化，无法随时得到准确的参数。

由上可知，现有的技术方案无法有效的获取波浪能发电系统的最大输出有功功率。

技术实现要素：

有鉴于此，本发明提供一种波浪能发电系统最大输出有功功率的捕获方法及装置，以解决现有的技术方案无法有效的获取波浪能发电系统的最大输出有功功率的问题。技术方案如下：

一种波浪能发电系统最大输出有功功率的捕获方法，所述方法包括：

对波浪能发电系统中发电机的反电磁力F_g在频域角度进行分析，获取所述发电机的反电磁力函数F_g(ω)的表达式：

$F_g\left(\mathrm{\ω}\right)=-Z_g\left(\mathrm{\ω}\right)\stackrel{\·}{x}\left(\mathrm{\ω}\right)$

其中，Z_g(ω)为所述发电机的等效阻抗，为所述波浪能发电系统在垂直方向上偏离平衡位置的位移的微分；

Z_g(ω)的表达式为：

$Z_g\left(\mathrm{\ω}\right)=R_g+{\mathrm{jX}}_g=R_g-j\frac{K_g}{\mathrm{\ω}}$

其中，R_g为所述发电机等效阻抗中的电阻；K_g为所述发电机等效阻抗中的电容；

根据波浪能发电系统的频域动态方程与所述发电机的反电磁力函数F_g(ω)的表达式，将波浪能发电系统输出有功功率P_g(ω)的表达式

$\stackrel{\‾}{P_g\left(\mathrm{\ω}\right)}=-\mathrm{Re}\[\frac{1}{\sqrt{2}}{F}_g\left(\mathrm{\ω}\right).\frac{1}{\sqrt{2}}{\stackrel{\·}{x}}^{*}\left(\mathrm{\ω}\right)\]$

转化为P_g(ω)与二维变量组[R_g,K_g]的计算关系表达式：

$\stackrel{\‾}{P_g\left({\mathrm{\ω}}_o\right)}=\[1-|\frac{1-R_g-j(1-\frac{K_g}{1})}{1+R_g+j(1-\frac{K_g}{1})}{|}^2\]$

根据P_g(ω)与二维变量组[R_g,K_g]的数学关系绘制P_g(ω)与二维变量组[R_g,K_g]的关系曲线图；

根据所述关系曲线图中曲线上各个点的斜率角将所述关系曲线图划分为多个不同区域，并确定各个不同区域的扰动步长；

以浮子位移的平衡点对应的所述波浪能发电系统输出有功功率的值作为初始值，采用扰动观察法根据所述关系曲线图上所述各个区域对应的扰动步长，在R_g和K_g两个维度上施加交替扰动，直到获取所述波浪能发电系统的最大输出有功功率。

优选的，所述对波浪能发电系统中发电机的反电磁力F_g在频域角度进行分析，获取所述发电机的反电磁力函数F_g(ω)的表达式，包括：

获取波浪能发电系统的时域动态方程：

$m\stackrel{\·\·}{x}\left(t\right)=f_e\left(t\right)+f_r\left(t\right)+f_b\left(t\right)+f_v\left(t\right)+f_f\left(t\right)+f_g\left(t\right)-mg$

其中，m为所述波浪能发电系统的总质量，t为时间，x(t)为所述波浪能发电系统在垂直方向上偏离平衡位置的位移的函数，f_e(t)为波浪作用在浮子上的力的函数，f_r(t)为辐射力函数，f_b(t)为静浮力函数，f_v(t)为粘滞力函数，f_f(t)为摩擦力函数，f_g(t)为所述波浪能发电系统中发电机的反电磁力函数，g为重力加速度；

对所述时域动态方程进行傅里叶变换，获取对应的频域动态方程：

$\[j\mathrm{\ω}(m+m_a(\mathrm{\ω}\left)\right)+R_a\left(\mathrm{\ω}\right)+\frac{1}{j\mathrm{\ω}}K\]\stackrel{\·}{x}\left(\mathrm{\ω}\right)=F_e\left(\mathrm{\ω}\right)+F_g\left(\mathrm{\ω}\right)$

其中，j为虚数单位，ω为波浪能发电系统的频率，m_a(ω)为由辐射力产生的附加质量函数，R_a(ω)为由辐射力产生的阻尼系数函数，K为浮子系数，F_e(ω)为波浪作用在浮子上的力的函数，F_g(ω)为所述发电机的反电磁力函数；

将所述频域动态方程转化为关于所述波浪能发电系统的等效阻抗Z_i的频域动态方程：

$Z_i\stackrel{\·}{x}\left(\mathrm{\ω}\right)=F_e\left(\mathrm{\ω}\right)+F_g\left(\mathrm{\ω}\right)$

所述

根据所述关于Z_i的频域动态方程，获取所述发电机的反电磁力函数F_g(ω)的表达式：

$F_g\left(\mathrm{\ω}\right)=-Z_g\left(\mathrm{\ω}\right)\stackrel{\·}{x}\left(\mathrm{\ω}\right)$

其中，Z_g(ω)为所述发电机的等效阻抗，为所述波浪能发电系统在垂直方向上偏离平衡位置的位移的微分。

优选的，所述根据所述关系曲线图中曲线上各个点的斜率角将所述关系曲线图划分为多个不同区域，并确定各个不同区域的扰动步长，包括：

获取所述关系曲线图中曲线上各个点的斜率角θ；

将60°<θ<＝120°的区域划分为快速变化区，并将所述快速变化区的扰动步长设置为第一预设步长；

将120°<θ<150°的区域划分为缓速变化区，并将所述缓速变化区的扰动步长设置为第二预设步长；

将0°<θ<＝60°或150°<＝θ<＝180°的区域划分为寻优区，并根据预设规则设置所述寻优区的扰动步长。

优选的，所述根据预设规则设置所述寻优区的扰动步长包括：

获取当前位于寻优区的点的斜率角θ；

将当前点在R_g维度上的扰动步长设置为10tanθ；

将当前点在K_g维度上的扰动步长设置为5tanθ。

优选的，所述以浮子位移的平衡点对应的所述波浪能发电系统输出有功功率的值作为初始值，采用扰动观察法根据所述关系曲线图上各个区域对应的扰动步长在R_g和K_g两个维度上施加交替扰动，直到获取所述波浪能发电系统的最大输出有功功率，包括：

S1：将所述初始值在所述关系曲线图上对应的点确定为对比点，并将所述对比点对应的波浪能发电系统的输出有功功率确定为对比功率；所述初始值为浮子位移的平衡点对应的所述波浪能发电系统输出有功功率的值；

S2：在维度R_g上获取目标点，并将所述目标点对应的波浪能发电系统的输出有功功率确定为目标功率；所述对比点与所述目标点为不同的点；

S3：判断所述目标点对应的目标功率是否为波浪能发电系统的最大输出有功功率；

S4：若是，输出所述目标点对应的二维变量组[R_g,K_g]；若否，比较对比功率与目标功率的大小，根据所述目标点的预设扰动步长，在不同于获取所述目标点的维度的另一维度上，沿着所述对比点与所述目标点的波浪能发电系统输出有功功率增大的方向获取下一个目标点，并将原目标点作为新的对比点，并返回S3。

一种波浪能发电系统最大输出有功功率的捕获装置，所述装置包括：

获取模块，用于对波浪能发电系统中发电机的反电磁力F_g在频域角度进行分析，获取所述发电机的反电磁力函数F_g(ω)的表达式：

$F_g\left(\mathrm{\&omega;}\right)=-Z_g\left(\mathrm{\&omega;}\right)\stackrel{\&CenterDot;}{x}\left(\mathrm{\&omega;}\right)$

其中，Z_g(ω)为所述发电机的等效阻抗，为所述波浪能发电系统在垂直方向上偏离平衡位置的位移的微分；

Z_g(ω)的表达式为：

$Z_g\left(\mathrm{\&omega;}\right)=R_g+{\mathrm{jX}}_g=R_g-j\frac{K_g}{\mathrm{\&omega;}}$

其中，R_g为所述发电机等效阻抗中的电阻；K_g为所述发电机等效阻抗中的电容；

转化模块，用于根据所述频域动态方程与所述发电机的反电磁力计算公式

将波浪能发电系统输出有功功率计算公式转化为所述波浪能发电系统输出有功功率与二维变量组[R_g,K_g]的计算关系公式：

$\stackrel{\&OverBar;}{P_g\left({\mathrm{\&omega;}}_o\right)}=\&lsqb;1-|\frac{1-R_g-j(1-\frac{K_g}{1})}{1+R_g+j(1-\frac{K_g}{1})}{|}^2\&rsqb;$

绘制模块，用于根据所述波浪能发电系统输出有功功率与二维变量组[R_g,K_g]的数学关系绘制所述波浪能发电系统输出有功功率与二维变量组[R_g,K_g]的关系曲线图；

划分模块，用于根据所述关系曲线图中曲线上各个点的斜率角将所述关系曲线图划分为多个不同区域，并确定各个不同区域的扰动步长；

扰动模块，用于以所述浮子位移的平衡点对应的所述波浪能发电系统输出有功功率的值作为初始值，采用扰动观察法根据所述关系曲线图上所述各个区域对应的扰动步长在R_g和K_g两个维度上施加交替扰动，直到获取所述波浪能发电系统的最大输出有功功率。

优选的，所述获取模块包括：

第一获取子模块，用于获取波浪能发电系统的时域动态方程：

$m\stackrel{\&CenterDot;\&CenterDot;}{x}\left(t\right)=f_e\left(t\right)+f_r\left(t\right)+f_b\left(t\right)+f_v\left(t\right)+f_f\left(t\right)+f_g\left(t\right)-mg$

其中，m为所述波浪能发电系统的总质量，t为时间，x(t)为所述波浪能发电系统在垂直方向上偏离平衡位置的位移的函数，f_e(t)为波浪作用在浮子上的力的函数，f_r(t)为辐射力函数，f_b(t)为静浮力函数，f_v(t)为粘滞力函数，f_f(t)为摩擦力函数，f_g(t)为所述波浪能发电系统中发电机的反电磁力函数，g为重力加速度；

傅里叶变换子模块，用于对所述时域动态方程进行傅里叶变换，获取对应的频域动态方程：

$\&lsqb;j\mathrm{\&omega;}(m+m_a(\mathrm{\&omega;}\left)\right)+R_a\left(\mathrm{\&omega;}\right)+\frac{1}{j\mathrm{\&omega;}}K\&rsqb;\stackrel{\&CenterDot;}{x}\left(\mathrm{\&omega;}\right)=F_e\left(\mathrm{\&omega;}\right)+F_g\left(\mathrm{\&omega;}\right)$

其中，j为虚数单位，ω为波浪能发电系统的频率，m_a(ω)为由辐射力产生的附加质量函数，R_a(ω)为由辐射力产生的阻尼系数函数，K为浮子系数，F_e(ω)为波浪作用在浮子上的力的函数，F_g(ω)为所述发电机的反电磁力函数；

转化子模块，用于将所述频域动态方程转化为关于所述波浪能发电系统的等效阻抗Z_i的频域动态方程：

$Z_i\stackrel{\&CenterDot;}{x}\left(\mathrm{\&omega;}\right)=F_e\left(\mathrm{\&omega;}\right)+F_g\left(\mathrm{\&omega;}\right)$

所述

第二获取子模块，用于根据所述关于Z_i的频域动态方程，获取所述发电机的反电磁力函数F_g(ω)的表达式：

$F_g\left(\mathrm{\&omega;}\right)=-Z_g\left(\mathrm{\&omega;}\right)\stackrel{\&CenterDot;}{x}\left(\mathrm{\&omega;}\right)$

其中，Z_g(ω)为所述发电机的等效阻抗，为所述波浪能发电系统在垂直方向上偏离平衡位置的位移的微分。

优选的，所述划分模块包括：

第三获取子模块，用于获取所述关系曲线图中曲线上各个点的斜率角θ；

第一划分子模块，用于将60°<θ<＝120°的区域划分为快速变化区，并将所述快速变化区的扰动步长设置为第一预设步长；

第二划分子模块，用于将120°<θ<150°的区域划分为缓速变化区，并将所述缓速变化区的扰动步长设置为第二预设步长；

第三划分子模块，将0°<θ<＝60°或150°<＝θ<＝180°的区域划分为寻优区，并根据预设规则设置所述寻优区的扰动步长。

优选的，所述第三划分子模块包括：

设置模块，用于获取当前位于寻优区的点的斜率角θ；将当前点在R_g维度上的扰动步长设置为10tanθ；将当前点在K_g维度上的扰动步长设置为5tanθ。

优选的，所述扰动模块包括：

确定子模块，用于将所述初始值在所述关系曲线图上对应的点确定为对比点，并将所述对比点对应的波浪能发电系统的输出有功功率确定为对比功率；所述初始值为浮子位移的平衡点对应的所述波浪能发电系统输出有功功率的值；

第四获取子模块，用于在维度R_g上获取目标点，并将所述目标点对应的波浪能发电系统的输出有功功率确定为目标功率；所述对比点与所述目标点为不同的点；

判断子模块，用于判断所述目标点对应的目标功率是否为波浪能发电系统的最大输出有功功率；若是，输出所述目标点对应的二维变量组[R_g,K_g]；若否，比较对比功率与目标功率的大小，根据所述目标点的预设扰动步长，在不同于获取所述目标点的维度的另一维度上，沿着所述对比点与所述目标点的波浪能发电系统输出有功功率增大的方向获取下一个目标点，并将原目标点作为新的对比点，并重新判断新的目标点对应的目标功率是否为波浪能发电系统的最大输出有功功率。

本发明提供的方法，对波浪能发电系统的运动状态进行频域分析，得出所述波浪能发电系统的输出有功功率与一个[R_g,K_g]的二维变量组有关，R_g为所述发电机等效阻抗中的电阻；K_g为所述发电机等效阻抗中的电容；通过扰动观察法在R_g和K_g两个维度上施加交替扰动不断快速寻求所述波浪能发电系统的最大输出有功功率运行点，在无法得知波浪能发电系统准确参数的情况下，调整波浪能发电系统的等效阻抗，使所述波浪能发电系统始终捕获最大输出有功功率。且本发明中在所述关系曲线图中分区域设置不同的扰动步长，根据斜率的变化改变扰动步长，使波浪能发电系统快速稳定在最大输出有功功率点。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据提供的附图获得其他的附图。

图1为本发明公开的一种波浪能发电系统最大输出有功功率的捕获方法流程图；

图2为本发明公开的一种波浪能发电系统最大输出有功功率的捕获方法又一方法流程图；

图3为本发明公开的一种波浪能发电系统最大输出有功功率的捕获方法又一方法流程图；

图4为本发明公开的一种波浪能发电系统最大输出有功功率的捕获方法又一方法流程图；

图5为本发明公开的一种波浪能发电系统最大输出有功功率的捕获方法又一方法流程图；

图6为本发明公开的一种波浪能发电系统最大输出有功功率的捕获装置结构示意图；

图7为本发明公开的另一种波浪能发电系统最大输出有功功率的捕获装置结构示意图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

请参阅图1，图1为本发明公开的一种波浪能发电系统最大输出有功功率的捕获方法流程图，所述方法包括以下步骤：

步骤S101：对波浪能发电系统中发电机的反电磁力F_g在频域角度进行分析，获取所述发电机的反电磁力函数F_g(ω)的表达式：

$F_g\left(\mathrm{\&omega;}\right)=-Z_g\left(\mathrm{\&omega;}\right)\stackrel{\&CenterDot;}{x}\left(\mathrm{\&omega;}\right)$

其中，Z_g(ω)为所述发电机的等效阻抗，为所述波浪能发电系统在垂直方向上偏离平衡位置的位移的微分；

Z_g(ω)的表达式为：

$Z_g\left(\mathrm{\&omega;}\right)=R_g+{\mathrm{jX}}_g=R_g-j\frac{K_g}{\mathrm{\&omega;}}$

其中，R_g为所述发电机等效阻抗中的电阻；K_g为所述发电机等效阻抗中的电容；

步骤S102：根据波浪能发电系统的频域动态方程与所述发电机的反电磁力函数F_g(ω)的表达式，将波浪能发电系统输出有功功率P_g(ω)的表达式

$\stackrel{\&OverBar;}{P_g\left(\mathrm{\&omega;}\right)}=-\mathrm{Re}\&lsqb;\frac{1}{\sqrt{2}}{F}_g\left(\mathrm{\&omega;}\right).\frac{1}{\sqrt{2}}{\stackrel{\&CenterDot;}{x}}^{*}\left(\mathrm{\&omega;}\right)\&rsqb;$

转化为P_g(ω)与二维变量组[R_g,K_g]的计算关系表达式：

$\stackrel{\&OverBar;}{P_g\left({\mathrm{\&omega;}}_o\right)}=\&lsqb;1-|\frac{1-R_g-j(1-\frac{K_g}{1})}{1+R_g+j(1-\frac{K_g}{1})}{|}^2\&rsqb;$

步骤S103：根据P_g(ω)与二维变量组[R_g,K_g]的数学关系绘制P_g(ω)与二维变量组[R_g,K_g]的关系曲线图；

具体的，所述关系图为一个三维曲线图。

步骤S104：根据所述关系曲线图中曲线上各个点的斜率角将所述关系曲线图划分为多个不同区域，并确定各个不同区域的扰动步长；

步骤S105：以所述浮子位移的平衡点对应的所述波浪能发电系统输出有功功率的值作为初始值，采用扰动观察法根据所述关系曲线图上所述各个区域对应的扰动步长，在R_g和K_g两个维度上施加交替扰动，直到获取所述波浪能发电系统的最大输出有功功率。

具体的，所述浮子位移的平衡点为浮子相对于水面静止的点。

优选的，所述波浪能发电系统的最大输出有功功率对应的点在所述关系曲线图上的斜率为0。

以上为本发明提供的一种波浪能发电系统最大输出有功功率的捕获方法，对波浪能发电系统中发电机的反电磁力F_g在频域角度进行分析，获取所述发电机的反电磁力函数F_g(ω)的表达式，根据波浪能发电系统的频域动态方程与所述发电机的反电磁力函数F_g(ω)的表达式，将波浪能发电系统输出有功功率P_g(ω)的表达式转化为P_g(ω)与二维变量组[R_g,K_g]的计算关系表达式，根据所述波浪能发电系统的输出有功功率与二维变量组[R_g,K_g]的数学关系绘制关系曲线图，根据曲线图上点的斜率的不同将所述关系曲线图划分为不同区域，并在不同区域设置不同的扰动步长，在R_g和K_g两个维度上施加交替扰动，直到获得波浪能发电系统的最大输出有功功率。

本发明提供的方法，对波浪能发电系统的运动状态进行频域分析，得出所述波浪能发电系统的输出有功功率与一个[R_g,K_g]的二维变量组有关，R_g为所述发电机等效阻抗中的电阻；K_g为所述发电机等效阻抗中的电容；通过扰动观察法在R_g和K_g两个维度上施加交替扰动不断快速寻求所述波浪能发电系统的最大输出有功功率运行点，在无法得知波浪能发电系统准确参数的情况下，调整波浪能发电系统的等效阻抗，始终进行最大输出有功功率捕获的目的。且本发明中在所述关系曲线图中分区域设置不同的扰动步长，根据斜率的变化改变扰动步长，使波浪能发电系统快速稳定在最大输出有功功率点。

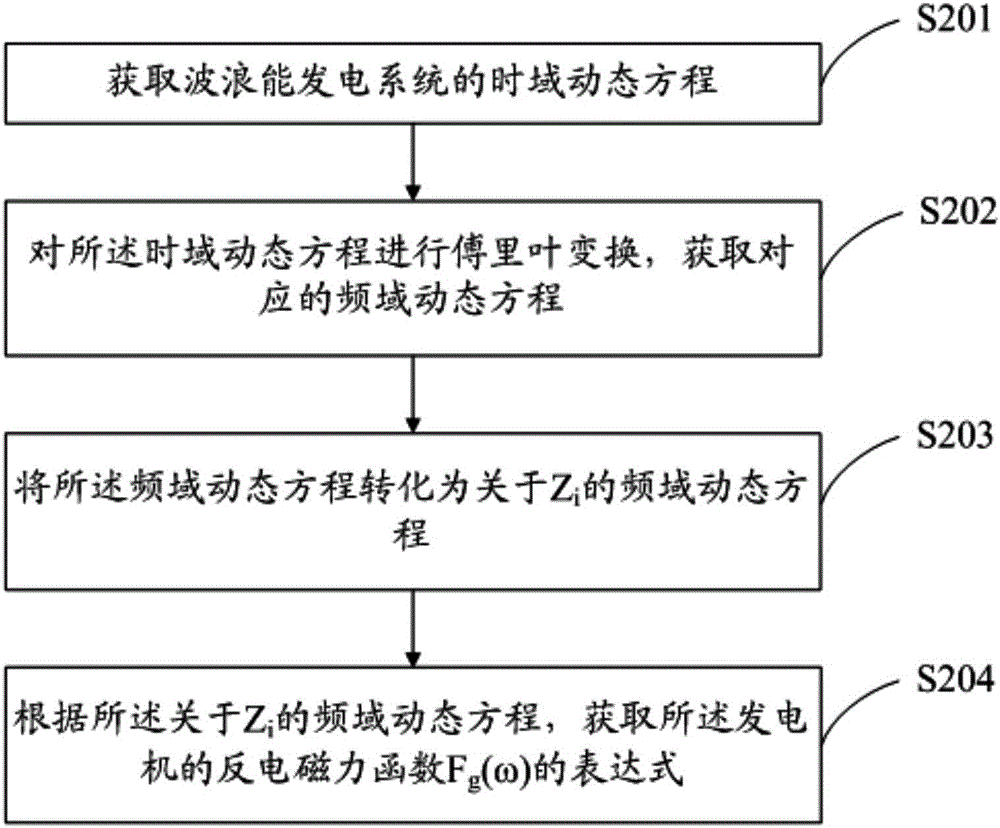
请参阅图2，对波浪能发电系统中发电机的反电磁力F_g在频域角度进行分析，获取所述发电机的反电磁力函数F_g(ω)的表达式，具体包括以下步骤：

步骤S201：获取波浪能发电系统的时域动态方程：

$m\stackrel{\&CenterDot;\&CenterDot;}{x}\left(t\right)=f_e\left(t\right)+f_r\left(t\right)+f_b\left(t\right)+f_v\left(t\right)+f_f\left(t\right)+f_g\left(t\right)-mg$

其中，m为所述波浪能发电系统的总质量，t为时间，x(t)为所述波浪能发电系统在垂直方向上偏离平衡位置的位移的函数，f_e(t)为波浪作用在浮子上的力的函数，f_r(t)为辐射力函数，f_b(t)为静浮力函数，f_v(t)为粘滞力函数，f_f(t)为摩擦力函数，f_g(t)为所述波浪能发电系统中发电机的反电磁力函数，g为重力加速度；

步骤S202：对所述时域动态方程进行傅里叶变换，获取对应的频域动态方程：

$\&lsqb;j\mathrm{\&omega;}(m+m_a(\mathrm{\&omega;}\left)\right)+R_a\left(\mathrm{\&omega;}\right)+\frac{1}{j\mathrm{\&omega;}}K\&rsqb;\stackrel{\&CenterDot;}{x}\left(\mathrm{\&omega;}\right)=F_e\left(\mathrm{\&omega;}\right)+F_g\left(\mathrm{\&omega;}\right)$

其中，j为虚数单位，ω为波浪能发电系统的频率，m_a(ω)为由辐射力产生的附加质量函数，R_a(ω)为由辐射力产生的阻尼系数函数，K为浮子系数，F_e(ω)为波浪作用在浮子上的力的函数，F_g(ω)为所述发电机的反电磁力函数；

步骤S203：将所述频域动态方程转化为关于所述波浪能发电系统的等效阻抗Z_i的频域动态方程：

$Z_i\stackrel{\&CenterDot;}{x}\left(\mathrm{\&omega;}\right)=F_e\left(\mathrm{\&omega;}\right)+F_g\left(\mathrm{\&omega;}\right)$

所述

步骤S204：根据所述关于Z_i的频域动态方程，获取所述发电机的反电磁力函数F_g(ω)的表达式：

$F_g\left(\mathrm{\&omega;}\right)=-Z_g\left(\mathrm{\&omega;}\right)\stackrel{\&CenterDot;}{x}\left(\mathrm{\&omega;}\right)$

其中，Z_g(ω)为所述发电机的等效阻抗，为所述波浪能发电系统在垂直方向上偏离平衡位置的位移的微分。

具体的，将波浪能发电系统从时域角度转换到频域角度，利用傅里叶变换，可得：

$\&lsqb;j\mathrm{\&omega;}(m+m_a(\mathrm{\&omega;}\left)\right)+R_a\left(\mathrm{\&omega;}\right)+\frac{1}{j\mathrm{\&omega;}}K\&rsqb;\stackrel{\&CenterDot;}{x}\left(\mathrm{\&omega;}\right)=F_e\left(\mathrm{\&omega;}\right)+F_g\left(\mathrm{\&omega;}\right)---\left(1\right)$

Zi为所述波浪能发电系统的等效阻抗，令Zi的表达式为：

$Z_i\left(\mathrm{\&omega;}\right)=R_a\left(\mathrm{\&omega;}\right)+j\mathrm{\&omega;}\&lsqb;(m+m_a(\mathrm{\&omega;}\left)\right)+\frac{K}{{\left(j\mathrm{\&omega;}\right)}^2}\&rsqb;=R_i\left(\mathrm{\&omega;}\right)+{\mathrm{jX}}_i\left(\mathrm{\&omega;}\right)---\left(2\right)$

将所述频域动态方程转化为关于Z_i的频域动态方程：

$Z_i\stackrel{\&CenterDot;}{x}\left(\mathrm{\&omega;}\right)=F_e\left(\mathrm{\&omega;}\right)+F_g\left(\mathrm{\&omega;}\right)$

通过观察上述Z_i的形式可以发现，Z_i的形式与电路中的阻抗相类似，且波浪能发电系统在垂直方向上偏离平衡位置的位移的微分，即波浪能发电机的速度，与电流类似，所述发电机的反电磁力与电压源类似，所以，为了易于实现所述发电机反电磁力的计算，将所述发电机的反电磁力确定为所述发电机的等效阻抗与波浪能发电系统在垂直方向上偏离平衡位置的位移的微分的乘积，获取所述发电机的反电磁力计算公式：

$F_g\left(\mathrm{\&omega;}\right)=-Z_g\left(\mathrm{\&omega;}\right)\stackrel{\&CenterDot;}{x}\left(\mathrm{\&omega;}\right)---\left(3\right)$

其中，Z_g(ω)为所述发电机的等效阻抗；

Z_g(ω)的表达式为：

$Z_g\left(\mathrm{\&omega;}\right)=R_g+{\mathrm{jX}}_g=R_g-j\frac{K_g}{\mathrm{\&omega;}}---\left(4\right)$

将式(2)-(4)代入所述波浪能发电系统的频域动态方程式(1)中，可得：

$\&lsqb;Z_i\left(\mathrm{\&omega;}\right)+Z_g\left(\mathrm{\&omega;}\right)\&rsqb;\stackrel{\&CenterDot;}{x}\left(\mathrm{\&omega;}\right)=F_e\left(\mathrm{\&omega;}\right)---\left(5\right)$

实际中，电路系统频域分析中取复功率的实部作为系统的输出有功功率，也就是平均功率。相对应于电路系统，波浪能发电系统也可以采用上述方法得出从波浪能中所提取到的输出有功功率，如下式所示：

$\stackrel{\&OverBar;}{P_g\left(\mathrm{\&omega;}\right)}=-\mathrm{Re}\&lsqb;\frac{1}{\sqrt{2}}{F}_g\left(\mathrm{\&omega;}\right).\frac{1}{\sqrt{2}}{\stackrel{\&CenterDot;}{x}}^{*}\left(\mathrm{\&omega;}\right)\&rsqb;---\left(6\right)$

式中*代表共轭。

对上式(6)进行化简，可得：

$\stackrel{\&OverBar;}{P_g\left(\mathrm{\&omega;}\right)}=\frac{|F_e\left(\mathrm{\&omega;}\right){|}^2}{8R_i\left(\mathrm{\&omega;}\right)}\&lsqb;1-|\frac{Z_i^{*}\left(\mathrm{\&omega;}\right)-Z_g\left(\mathrm{\&omega;}\right)}{Z_i\left(\mathrm{\&omega;}\right)+Z_g\left(\mathrm{\&omega;}\right)}{|}^2\&rsqb;---\left(7\right)$

对上式(7)进行分析，可以看出，在频域分析中，从波浪能中提取到的输出有功功率P_g(ω)与波浪能发电系统除发电机外其他部分的等效阻抗Z_i以及所述发电机的等效阻抗Z_g有着明确的数学关系。

在上式中，输出有功功率P_g(ω)有着一个最大值P_gmax(ω)：

$\stackrel{\&OverBar;}{P_{gmax}\left(\mathrm{\&omega;}\right)}=\frac{|F_e\left(\mathrm{\&omega;}\right){|}^2}{8R_i\left(\mathrm{\&omega;}\right)}---\left(8\right)$

令：

$\mathrm{\&beta;}=\&lsqb;1-|\frac{Z_i^{*}\left(\mathrm{\&omega;}\right)-Z_g\left(\mathrm{\&omega;}\right)}{Z_i\left(\mathrm{\&omega;}\right)+Z_g\left(\mathrm{\&omega;}\right)}{|}^2\&rsqb;---\left(9\right)$

可以看出β反映了波浪能发电系统从波浪能中所提取到的输出有功功率的占比。为使得β＝1，即捕获到最大波浪能，必须满足以下条件：

$Z_i^{*}\left(\mathrm{\&omega;}\right)=Z_g\left(\mathrm{\&omega;}\right)---\left(10\right)$

式(10)反映了波浪能发电系统在达到最大波浪能捕获时的状态，从物理上来描述，当波浪能发电系统中负责功率输出的部分，也就是发电机，其等效阻抗与波浪能发电系统波能捕获部分的等效阻抗相匹配时，满足最大功率传输条件。

在稳定情况下的海洋区域，较长一段时间内波浪都处于缓慢变化状态。因此，可以把该状态下的波浪运动简化成具有稳定频率ω_o的运动。该情况下，波浪纵向方向运动给浮子所带来的附加质量m_a以及产生的阻尼系数R_a都具有稳定值为：

m_a＝m_a(ω_o)

R_a＝R_a(ω_o)

(11)

把式(11)代入式(2)中得：

$Z_i\left({\mathrm{\&omega;}}_o\right)=R_i\left({\mathrm{\&omega;}}_o\right)+{\mathrm{jX}}_i\left({\mathrm{\&omega;}}_o\right)=R_a\left({\mathrm{\&omega;}}_o\right)+j\&lsqb;{\mathrm{\&omega;}}_o(m+m_a({\mathrm{\&omega;}}_o\left)\right)-\frac{K}{{\mathrm{\&omega;}}_o}\&rsqb;---\left(12\right)$

式(12)反映了在稳态情况下波浪捕获结构等效阻抗的稳态值，从中可以看出该等效阻抗与波浪运动的频率直接相关。

为了得出P_g(ω)与Z_i以及Z_g在稳态下的关系，把式(4)式(12)代入式(7)中

观察式(13)，在稳定波浪频率下，ω_o，|F_e(ω_o)|以及R_i(ω_o)和X_i(ω_o)均具有一个由波浪捕获结构的物理特性和波浪频率决定的确定值。为了对式(13)进行具体分析，式(13)中波浪频率、最大提取功率、能量捕获结构等效阻抗都标幺化，简化后可得：

$\stackrel{\&OverBar;}{P_g\left({\mathrm{\&omega;}}_o\right)}=\&lsqb;1-|\frac{1-R_g-j(1-\frac{K_g}{1})}{1+R_g+j(1-\frac{K_g}{1})}{|}^2\&rsqb;---\left(14\right)$

请参阅图3，所述根据所述关系曲线图中曲线上各个点的斜率角将所述关系曲线图划分为多个不同区域，并确定各个不同区域的扰动步长，具体包括以下步骤：

步骤S301：获取所述关系曲线图中曲线上各个点的斜率角θ；

步骤S302：将60°<θ<＝120°的区域划分为快速变化区，并将所述快速变化区的扰动步长设置为第一预设步长；

具体的，在快速变化区变量较小的变化都会引起功率的显著的变化，特别是在最大功率点附近，会引起扰动的剧烈变化，为了避免在最大功率点附近产生剧烈振荡，在快速变化区采用一个较小的步长。

优选的，所述第一预设步长为0.05。

步骤S303：将120°<θ<150°的区域划分为缓速变化区，并将所述缓速变化区的扰动步长设置为第二预设步长；

具体的，在缓速变化区域上，小步长扰动会使波浪能发电系统寻找最大功率点的速度大大下降，在效率上不能够满足要求。为了使波浪能发电系统快速过渡，跳出缓速变化区域，在缓速变化区域上采用一个较大的步长。

优选的，所述第二预设步长为3。

步骤S304：将0°<θ<＝60°或150°<＝θ<＝180°的区域划分为寻优区，并根据预设规则设置所述寻优区的扰动步长。

具体的，在寻优区根据斜率的变化改变步长，使波浪能发电系统快速稳定在最大功率点附近。

优选的，如图4所示，所述根据预设规则计算所述寻优区的扰动步长包括：

步骤S401：获取当前位于寻优区的点的斜率角θ；

步骤S402：将当前点在R_g维度上的扰动步长设置为10tanθ；

步骤S403：将当前点在K_g维度上的扰动步长设置为5tanθ。

请参阅图5，所述以所述浮子位移的平衡点对应的所述波浪能发电系统输出有功功率的值作为初始值，采用扰动观察法根据所述关系曲线图上各个区域对应的扰动步长在Rg和Kg两个维度上施加交替扰动，直到获取所述波浪能发电系统的最大输出有功功率，具体包括以下步骤：

步骤S501：S1：将所述初始值在所述关系曲线图上对应的点确定为对比点，并将所述对比点对应的波浪能发电系统的输出有功功率确定为对比功率；所述初始值为浮子位移的平衡点对应的所述波浪能发电系统输出有功功率的值；

步骤S502：S2：在维度R_g上获取目标点，并将所述目标点对应的波浪能发电系统的输出有功功率确定为目标功率；所述对比点与所述目标点为不同的点；

步骤S503：S3：判断所述目标点对应的目标功率是否为波浪能发电系统的最大输出有功功率；

步骤S504：S4：若是，输出所述目标点对应的二维变量组[R_g,K_g]；若否，比较对比功率与目标功率的大小，根据所述目标点的预设扰动步长，在不同于获取所述目标点的维度的另一维度上，沿着所述对比点与所述目标点的波浪能发电系统输出有功功率增大的方向获取下一个目标点，并将原目标点作为新的对比点，并返回S3。

本发明公开的波浪能发电系统最大输出有功功率的捕获方法，通过变步长扰动观察法在R_g和K_g两个维度上施加交替扰动不断快速寻求波浪能发电系统的最大输出有功功率运行点，在无法得知波浪能发电系统准确参数的情况下，动态调整波浪能发电系统的等效阻抗，始终能够捕获到最大输出有功功率。

基于上述本发明公开的一种波浪能发电系统最大输出有功功率的捕获方法，请参阅图6，本发明对应公开了一种波浪能发电系统最大输出有功功率的捕获装置，包括：

获取模块101，用于对波浪能发电系统中发电机的反电磁力F_g在频域角度进行分析，获取所述发电机的反电磁力函数F_g(ω)的表达式：

$F_g\left(\mathrm{\&omega;}\right)=-Z_g\left(\mathrm{\&omega;}\right)\stackrel{\&CenterDot;}{x}\left(\mathrm{\&omega;}\right)$

其中，Z_g(ω)为所述发电机的等效阻抗，为所述波浪能发电系统在垂直方向上偏离平衡位置的位移的微分；

Z_g(ω)的表达式为：

$Z_g\left(\mathrm{\&omega;}\right)=R_g+{\mathrm{jX}}_g=R_g-j\frac{K_g}{\mathrm{\&omega;}}$

其中，R_g为所述发电机等效阻抗中的电阻；K_g为所述发电机等效阻抗中的电容；

转化模块102，用于根据所述频域动态方程与所述发电机的反电磁力计算公式将波浪能发电系统输出有功功率计算公式

转化为所述波浪能发电系统输出有功功率与二维变量组[R_g,K_g]的计算关系公式：

$\stackrel{\&OverBar;}{P_g\left({\mathrm{\&omega;}}_o\right)}=\&lsqb;1-|\frac{1-R_g-j(1-\frac{K_g}{1})}{1+R_g+j(1-\frac{K_g}{1})}{|}^2\&rsqb;$

绘制模块103，用于根据所述波浪能发电系统输出有功功率与二维变量组[R_g,K_g]的数学关系绘制所述波浪能发电系统输出有功功率与二维变量组[R_g,K_g]的关系曲线图；

划分模块104，用于根据所述关系曲线图中曲线上各个点的斜率角将所述关系曲线图划分为多个不同区域，并确定各个不同区域的扰动步长；

扰动模块105，用于以所述浮子位移的平衡点对应的所述波浪能发电系统输出有功功率的值作为初始值，采用扰动观察法根据所述关系曲线图上所述各个区域对应的扰动步长在R_g和K_g两个维度上施加交替扰动，直到获取所述波浪能发电系统的最大输出有功功率。

以上为本发明提供的一种波浪能发电系统最大输出有功功率的捕获装置，对波浪能发电系统中发电机的反电磁力F_g在频域角度进行分析，获取所述发电机的反电磁力函数F_g(ω)的表达式，根据波浪能发电系统的频域动态方程与所述发电机的反电磁力函数F_g(ω)的表达式，将波浪能发电系统输出有功功率P_g(ω)的表达式转化为P_g(ω)与二维变量组[R_g,K_g]的计算关系表达式，根据所述波浪能发电系统的输出有功功率与二维变量组[R_g,K_g]的数学关系绘制关系曲线图，根据曲线图上点的斜率的不同将所述关系曲线图划分为不同区域，并在不同区域设置不同的扰动步长，在R_g和K_g两个维度上施加交替扰动，直到获得波浪能发电系统的最大输出有功功率。

本发明提供的装置，对波浪能发电系统的运动状态进行频域分析，得出所述波浪能发电系统的输出有功功率与一个[R_g,K_g]的二维变量组有关，R_g为所述发电机等效阻抗中的电阻；K_g为所述发电机等效阻抗中的电容；通过扰动观察法在R_g和K_g两个维度上施加交替扰动不断快速寻求所述波浪能发电系统的最大输出有功功率运行点，在无法得知波浪能发电系统准确参数的情况下，调整波浪能发电系统的等效阻抗，始终进行最大输出有功功率捕获的目的。且本发明中在所述关系曲线图中分区域设置不同的扰动步长，根据斜率的变化改变扰动步长，使波浪能发电系统快速稳定在最大输出有功功率点。

请参阅图7，所述获取模块101包括：

第一获取子模块106，用于获取波浪能发电系统的时域动态方程：

$m\stackrel{\&CenterDot;\&CenterDot;}{x}\left(t\right)=f_e\left(t\right)+f_r\left(t\right)+f_b\left(t\right)+f_v\left(t\right)+f_f\left(t\right)+f_g\left(t\right)-mg$

其中，m为所述波浪能发电系统的总质量，t为时间，x(t)为所述波浪能发电系统在垂直方向上偏离平衡位置的位移的函数，f_e(t)为波浪作用在浮子上的力的函数，f_r(t)为辐射力函数，f_b(t)为静浮力函数，f_v(t)为粘滞力函数，f_f(t)为摩擦力函数，f_g(t)为所述波浪能发电系统中发电机的反电磁力函数，g为重力加速度；

傅里叶变换子模块107，用于对所述时域动态方程进行傅里叶变换，获取对应的频域动态方程：

$\&lsqb;j\mathrm{\&omega;}(m+m_a(\mathrm{\&omega;}\left)\right)+R_a\left(\mathrm{\&omega;}\right)+\frac{1}{j\mathrm{\&omega;}}K\&rsqb;\stackrel{\&CenterDot;}{x}\left(\mathrm{\&omega;}\right)=F_e\left(\mathrm{\&omega;}\right)+F_g\left(\mathrm{\&omega;}\right)$

其中，j为虚数单位，ω为波浪能发电系统的频率，m_a(ω)为由辐射力产生的附加质量函数，R_a(ω)为由辐射力产生的阻尼系数函数，K为浮子系数，F_e(ω)为波浪作用在浮子上的力的函数，F_g(ω)为所述发电机的反电磁力函数；

转化子模块108，用于将所述频域动态方程转化为关于所述波浪能发电系统的等效阻抗Z_i的频域动态方程：

$Z_i\stackrel{\&CenterDot;}{x}\left(\mathrm{\&omega;}\right)=F_e\left(\mathrm{\&omega;}\right)+F_g\left(\mathrm{\&omega;}\right)$

所述

第二获取子模块109，用于根据所述关于Z_i的频域动态方程，获取所述发电机的反电磁力函数F_g(ω)的表达式：

$F_g\left(\mathrm{\&omega;}\right)=-Z_g\left(\mathrm{\&omega;}\right)\stackrel{\&CenterDot;}{x}\left(\mathrm{\&omega;}\right)$

其中，Z_g(ω)为所述发电机的等效阻抗，为所述波浪能发电系统在垂直方向上偏离平衡位置的位移的微分。

所述划分模块104包括：

第三获取子模块110，用于获取所述关系曲线图中曲线上各个点的斜率角θ；

第一划分子模块111，用于将60°<θ<＝120°的区域划分为快速变化区，并将所述快速变化区的扰动步长设置为第一预设步长；

第二划分子模块112，用于将120°<θ<150°的区域划分为缓速变化区，并将所述缓速变化区的扰动步长设置为第二预设步长；

第三划分子模块113，将0°<θ<＝60°或150°<＝θ<＝180°的区域划分为寻优区，并根据预设规则设置所述寻优区的扰动步长。

优选的，所述第三划分子模块113包括：

设置模块，用于获取当前位于寻优区的点的斜率角θ；将当前点在R_g维度上的扰动步长设置为10tanθ；将当前点在K_g维度上的扰动步长设置为5tanθ。

所述扰动模块105包括：

确定子模块114，用于将所述初始值在所述关系曲线图上对应的点确定为对比点，并将所述对比点对应的波浪能发电系统的输出有功功率确定为对比功率；所述初始值为浮子位移的平衡点对应的所述波浪能发电系统输出有功功率的值；

第四获取子模块115，用于在维度R_g上获取目标点，并将所述目标点对应的波浪能发电系统的输出有功功率确定为目标功率；所述对比点与所述目标点为不同的点；

判断子模块116，用于判断所述目标点对应的目标功率是否为波浪能发电系统的最大输出有功功率；若是，输出所述目标点对应的二维变量组[R_g,K_g]；若否，比较对比功率与目标功率的大小，根据所述目标点的预设扰动步长，在不同于获取所述目标点的维度的另一维度上，沿着所述对比点与所述目标点的波浪能发电系统输出有功功率增大的方向获取下一个目标点，并将原目标点作为新的对比点，并重新判断新的目标点对应的目标功率是否为波浪能发电系统的最大输出有功功率。

对所公开的实施例的上述说明，使本领域专业技术人员能够实现或使用本发明。对这些实施例的多种修改对本领域的专业技术人员来说将是显而易见的，本文中所定义的一般原理可以在不脱离本发明的精神或范围的情况下，在其它实施例中实现。因此，本发明将不会被限制于本文所示的这些实施例，而是要符合与本文所公开的原理和新颖特点相一致的最宽的范围。