电磁波与孔缝腔体内复杂传输线耦合预测方法与流程

本发明针对雷达电磁波与孔缝腔体内复杂传输线(TL)耦合预测问题，提出一种基于矩量法(MOM)、并矢格林函数(GF)和传输线PI等效电路与Agrawal混合模型的预测方法，属于微波和电磁兼容领域。
背景技术：
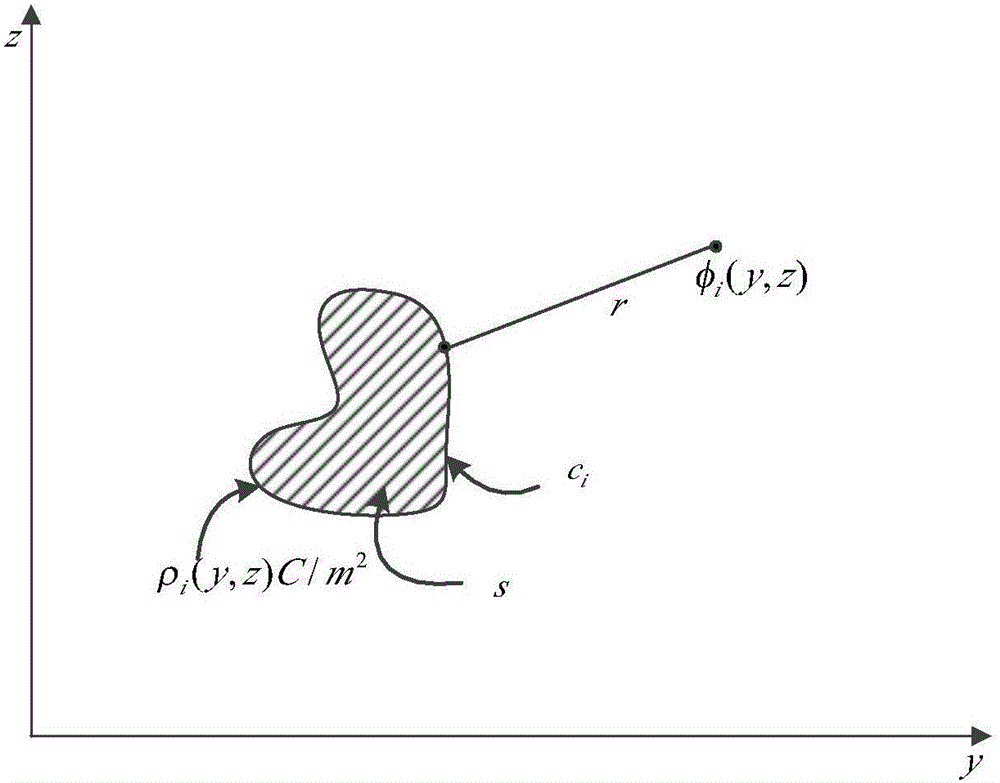
：随着电子科学技术的发展,海战场上的电磁环境逐渐变得恶劣,敏感设备越来越容易受电磁波干扰，房间内雷达设施或电子箱内设备也易受到干扰。房间或箱体等腔体由于通风散热口等需要,不可避免存在孔缝,这使得电磁波可通过腔体的孔缝耦合到腔体内。故电磁场通过孔缝对腔体内线缆的耦合响应已经是EMC领域的重要问题。很多学者已经对此类问题作出大量的研究，主要分为数值方法、混合算法和解析算法。数值算法虽然准确，但是耗费很大，计算时间较长，不能满足计算的快速性。有人提出一种基于电磁场下BLT方程求解传输线的负载响应的混合算法，但是BLT混合算法有时不能求解复杂传输线的耦合响应。本发明分析电磁波对房间这一大腔体内的复杂分布的传输线耦合，用MOM求得雷达天线产生的入射电磁场；采用MOM-GF混合算法计算孔缝处等效磁流并求得腔体内的电磁场；接着运用所得电磁场与传输线混合模型计算传输线的负载电流响应。技术实现要素：本发明针对雷达电磁波与孔缝腔体内复杂传输线耦合预测问题，提出一种基于矩量法(MOM)、并矢格林函数和传输线等效电路与Agrawal混合模型的预测方法。本发明的目的是这样实现的：电磁波与孔缝腔体内复杂传输线耦合预测方法包括如下步骤：步骤1.运用MOM计算雷达天线入射电磁场；步骤2.利用MOM-GF分析孔缝腔体内电磁场；步骤3.对步骤2所述孔缝腔体内任意截面形状的多导体传输线电容、电感参数计算；步骤4.建立PI等效电路与Agrawal混合模型对传输线分析。步骤1所述计算电磁场的方法如下：(1):利用雷达天线表面积分方程建立雷达天线的电场模型；(2):用RWG基函数将目标电流展开得到线性方程组：[Z][I]＝[V]其中，Z为阻抗矩阵，I为待求电流系数，V为激励向量；(3):根据步骤(1)所述的电场模型采用步骤(2)所述的电流系数I得到雷达天线的辐射电场E；(4):根据步骤(3)所述的雷达天线辐射场电场求得磁场强度H：H=1η·r^×E]]>其中，为雷达天线远区某点的坐标向量；η≈377。步骤2所述孔缝腔体内电磁场的分析方法如下：1)：用脉冲基函数将孔缝分解为P(x)×Q(y)块面元，得到孔缝每个面元中心点的等效磁流；2)：根据步骤1)所述的孔缝每个面元中心点的等效磁流得到孔缝腔体内任意一点的电场：Exb=Σm,n[jZ0k0kxkzAmn+kyBmn]cos(kxx)sin(kyy)sin(kz·(z+c))]]>Eyb=Σm,n[jZ0k0kxkzAmn-kyBmn]sin(kxx)cos(kyy)sin(kz·(z+c))]]>Ezb=-Σm,njZ0kc2k0Amnsin(kxx)sin(kyy)cos(kz·(z+c))]]>其中，ϵn=1,n=02,n>0]]>Ixmn=∫sMxsin(kxx)cos(kyy)ds]]>Iymn=∫sMycos(kxx)sin(kyy)ds]]>kx=mπ/a;ky=nπ/b;kc2=kx2+ky2;]]>Z0为自由空间波阻抗；j为虚数单位；k0为自由空间波数；Y0为自由空间导纳；a，b和c分别为腔体的长、高和宽；Mx和My分别孔缝处x和y方向的等效磁流。步骤3所述多导体传输线电容、电感参数计算方法如下：运用传输线PI等效电路模型将n+1传输线多导体系统第i个导体传输线划分为Ni段,每一段的传输线通过矩量法求得电容、互容、自感和互感，其中，0<i≤n+1，i和n均为大于1的正整数。步骤4所述传输线分析方法如下：首先，运用传输线PI等效电路模型将传输线划分为N段，N为大于1的自然数；其次，将传输线网络分为多个多导体和单导体的集合，而电磁场对多导体和单导体传输线的耦合电压采用Agrawal模型求出；最后，根据耦合电压输出最后的电流响应。电磁波波与孔缝内复杂传输线耦合计算问题，单独运用全波算法耗费大、时间长，本发明提出一种基于矩量法、并矢格林函数和传输线PI等效电路与Agrawal混合模型的计算方法。该算法适用多导体的情况，对于解决电磁波通过孔缝耦合到其他敏感设备的分析具有很强的优势。附图说明图1：电磁波与孔缝腔体内多导体束传输线耦合模型；其中，A为雷达天线简化模型。图2：传输线第i个导体的截面图；图3：传输线PI等效电路模型。具体实施方式下面该方法作进一步的详细说明。步骤1.运用MOM计算雷达天线入射电磁场图1所示为一个电磁波与孔缝腔体内传输线耦合模型图。为便于计算，将雷达天线A用线天线代替，其长度L0、半径r0，激励源在天线中心，位置为P0(x0,y0,z0)。腔体是一个体积为a(x)×b(y)×c(z)的矩形腔体且默认腔体内外都为自由空间；孔缝也为矩形，面积等于l(x)×w(y)，其近原点坐标为(xa,yb,0)。传输线的长L、半径r、首末段负载Z1Z2。首先，运用矩量法计算位于P(x,y,0)的孔缝中心处的雷达电磁场。理想导体构成的天线表面电场积分方程：其中，为导体表面在点的单位矢量；为辐射电场；μ0为真空磁导率，ε0为真空介电值常数；为点的表面电流；k为波数；为并矢和为单位坐标向量；g(r,r′)＝e-ik|r-r′|/|r-r′|；j为虚数单位。用RWG基函数将目标电流展开得到线性方程组：[Z][I]＝[V](2)其中，Z为阻抗矩阵，I为待求电流系数，V为激励向量。阻抗矩阵的表达式为：其中，为第m条边对应的RWG基函数；ω＝2πf；ε、μ分别为电介质常数和磁导率。将求得的电流带入电场积分方程(1)可得入射电场根据理想导体的边界条件：可得天线的辐射电场。运用线天线远区辐射场电场强度与磁场强度关系可以求得磁场强度：H=1η·r^×E---(4)]]>其中，为远区某点的坐标向量。步骤2.利用MOM-GF分析腔体内电磁场为求孔缝腔体内的电磁场，根据Schelkunoff场等效原理，满足内外等效电流切向连续，在孔缝处引入等效磁流M(忽略传输线对其的影响)。腔体外的a区和腔体内b区等效磁流分别满足：其中，为入射电场；为磁流M在腔体外产生的电场；为腔体内产生的电场。根据公式(5)、(6)可知：其中，为与对应的磁场；为腔体内部磁场。其中，k0是自由空间波数；Y0为自由空间导纳；此处s为孔缝范围，而且为二维格林函数，只与x、y有关。其中，依据公式(7)-(9)可得：为求解此公式，用脉冲基函数将孔缝分解为P(x)×Q(y)块面元，即展开M，得到线性方程组：[Ya+Yb]·[M]＝[C](14)其中，[M]的元素为包含位置编号为(p,q)的面元上磁流的x、y分量，即Mxpq和Mypq[12,15]；[C]中元素为：其中，spq为编号(p,q)的面元范围。Ya、Yb分别为a和b区的广义导纳，由于等效磁流有x、y分量，故Ya、Yb有四个分量，即和求得每个面元中心点的等效磁流后，近似认为每个小面元上的等效磁流相等。运用下列公式可得腔体内任意一点的电场：Exb=Σm,n[jZ0k0kxkzAmn+kyBmn]cos(kxx)sin(kyy)sin(kz·(z+c))---(16)]]>Eyb=Σm,n[jZ0k0kxkzAmn-kyBmn]sin(kxx)cos(kyy)sin(kz·(z+c))---(17)]]>Ezb=-Σm,njZ0kc2k0Amnsin(kxx)sin(kyy)cos(kz·(z+c))---(18)]]>其中，ϵn=1,n=02,n>0---(20)]]>Ixmn=∫sMxsin(kxx)cos(kyy)dsIymn=∫sMycos(kxx)sin(kyy)ds---(21)]]>Z0为自由空间波阻抗；j为虚数单位；k0为自由空间波数；Y0为自由空间导纳；Mx和My分别孔缝处x和y方向的等效磁流。步骤3.任意截面形状的多导体传输线电容、电感参数计算对于平行均匀的传输线，每Δx长度段的单位长度电感和电容相同；对于非平行或非均匀的传输线每段是不同的，需要分别计算。传输线第i个导体的截面图如图2所示，是非圆的非规则截面，其沿着x轴方向放置。其电势与电荷密度满足积分形式的泊松方程：φi(y,z)=14πϵ∫∫siρi(y,z)r---(22)]]>式中，φi(y,z)为某点产生的电势；r为导体上电荷分布的某点与产生电势点的距离；ρi(y,z)C/m2为电荷密度；si为导体截面；ε为周围介质介电常数。对于非规则截面的传输线，无法直接求单位长度电容的解析解，在这里可以利用矩量法(MOM)求近似解。首先将导体表面电荷分布近似成沿着x轴划分为Ni个细丝电荷，每段电荷密度为ρik。根据传输线导体之间间距与导体半径之比大于4及以上时，导体表面电荷分布可视为近似均匀分布(对于不规则截面，可认为间距与最大半径之比大于4及以上),假设在导体表面存在均匀分布的未知的电荷密度ρi(y,z)(单位C/m2)，那么将导体全部电荷分布表现为基函数ρik的线性组合：ρi(y,z)=αi1ρi1(y,z)+αi2ρi2(y,z)+...+αiNiρiNi(y,z)=Σk=1Niαikρik(y,z)---(23)]]>式中，αik为电荷分布的具体水平，可以由第i个导体上的电势为φi的边界条件确定。x方向单位长度总电荷可以由该导体上各个子部分的电荷之和得到：qi=Σk=1Niαik∫ciρikdci---(24)]]>式中，ci是图2中导体截面边界。用脉冲法展开公式(12)，简化为：式中，是第i个导体中第k个子段的宽度。在第i个导体中，任意一点的电势都是所有未知电荷分布的贡献，可以将它们的关系写成如下的公式：φi(y,z)=ζi1αi1+ζi2αi2+...+ζiNiαiNi=Σk=1Niζikαik---(26)]]>式中，ζik是每个基函数单独对电势的贡献，即其值大小可由下列公式计算可得：dφi=-ρiln(r)2πϵdci⇒φi=-∫ciρiln(r)2πϵdci---(27)]]>式中，dφi为每个字段中心处的电势。对于一个n+1传输线多导体系统，每个导体上的电势是系统中全部电荷产生的电势，因此可得导体i的电势为：φi=Σi=0nΣk=1Niζikαik---(28)]]>其中，0<i≤n+1，n为大于1的正整数。根据展开系数，可以得到联立方程：Φ0...Φi...Φn=D00...D0j...D0n...............Di0...Dij...Din...............Dn0...Dnj...DnnA0...Ai...An---(29)]]>⇒A0...Ai...An=B00...B0j...B0n...............Bi0...Bij...Bin...............Bn0...Bnj...BnnΦ0...Φi...Φn---(30)]]>式中，Φi为第i个导体上的匹配点处的电势向量，值为(φi…φi…φi)T是一个Ni×1矩阵；Ai第i个导体上电荷分布的展开系数向量，其也是一个Ni×1的矩阵，值为B＝D-1。由公式(18)得到：Ai＝BijΦj(31)电荷分布qi、电势φi与广义电容矩阵C的关系,可以计算传输线之间的自容和互容：由公式(13)、(19)和(20)可以得到广义电容矩阵中元素的大小：式中，如果即导体i的各子段的宽度相同，记为那么公式(21)简化为：式中，∑Bij的值是子矩阵Bij所有元素之和。假设导体之间充满介电常数为εr的介质或非均匀介质：含介质的单位长度电容为C；不含介质的单位长度电容为C0；单位长度电感为L。它们之间的关系：均匀介质：非均匀介质：式中：εr,eff为有效介电常数。步骤4.建立PI等效电路与Agrawal混合模型对传输线分析首先，运用传输线PI等效电路模型将传输线划分为N段，如图3所示，N＝Nl+NL+Nr，Nl、Nr为首端和末端接地的分段数，NL为传输线的分段数；ΔL为每个分段的长度；li1,i1,i、ci1,i1,i分别为第i1个传输线第i段的单位自感和自容，li1,i2,i、ci1,i2,i分别为第i1个i2和传输线第i段的单位互感和互容，其值由步骤3可得，由此可得第i段的阻抗Zli和导纳Yci：Zli＝jωliΔL；Yci＝jωciΔL。由此可得所有传输线第i段阻抗Zli的元素：Zi1,i1,i＝jωli1,i1,iΔL；Zi1,i2,i＝jωli1,i2,iΔL。所有传输线第i段阻抗Yci的元素：Yi1,i1,i＝1/jωci1,i1,iΔL；Yi1,i2,i＝1/jωci1,i2,iΔL。将复杂的传输线网络分为多个多导体和单导体的集合，而电磁场对多导体和单导体传输线的耦合电压可用Agrawal模型求出[13]。在首端、末端的电压受电场Ey激励，其值可由下列公式求出：Vli=∫yli-1yliEy(xli,y,zli)dy;Vri=-∫yri-1yriEy(xri,y,zri)dy---(37)]]>Vxl(i1,i2,i)=∫xli1xli2Ex(x,yli,zli)dxVzl(i1,i2,i)=∫zli1zli2Ez(x,yli,zli)dx⇒Vdl(i1,i2,i)=V2xl(i1,i2,i)+V2zl(i1,i2,)---(38)]]>其中，Vli、Vri为首末端第i段的自感电压；xliylizlixriyri和zri分别为首末段第i段的位置坐标；为首端第i1和第i2个传输线第i段的互感电压，末端同首端方法可求。为求传输线上的耦合电压，首先将传输线上每一段分解为x、y和z轴的平方和的二次根，即：分别求x、y和z轴方向电压，最后再合成总电压。VxLi=∫xLi-1xLiEx(x,yLi,zLi)dx≈Ex(x,yLi,zLi)·ΔxLi---(39)]]>VyLi=∫yLi-1yLiEy(xLi,y,zLi)dy≈Ey(xLi,y,zLi)·ΔyLi---(40)]]>VzLi=∫zLi-1zLiEz(xLi,yLi,z)dz≈Ez(xLi,yLi,z)·ΔzLi---(41)]]>VLi=VxLi2+VyLi2+VzLi2---(42)]]>其中，VLi分别为第i段的x、y和z轴自感方向电压与自感总电压。互感电压大小求解方法同式(5.34)，将x、y和z轴方向电压合成总电压如同式(5.35)-(5.38)。为方便表示，将首段到末端每段电压用向量V1,V2…Vi…VN-1,VN编号，每段电流用I1、I2…Ii…IN-1、IN编号，Vi、Ii由n个传输线的第i段自电压电流和互电压电流构成。通过电压与电流的关系可得电流的大小：其中，Ei为单位向量，如果第i段时有传输线i1到达末端，则Ei第i段之后第i1个位置值为0。当前第1页1 2 3