一种风电场输出功率爬坡事件预测的系统及方法与流程

本发明属于风力发电及其并网的技术领域，尤其涉及一种风电场输出电功率爬坡事件预测的系统及方法。

背景技术：

风力发电在电力系统中的作用正在不断增强，然而由于风速具有随机波动的特性，风电输出功率在短时间内存在大幅度波动现象，称为风电爬坡事件。在含高比例风电的电力系统中，风电爬坡事件已严重威胁到电力系统的安全稳定运行，直接造成电网的经济损失，严重影响电力系统用发电的平衡，甚至造成大规模停电事故。为减小风电爬坡事件对电力系统稳定性的影响，提高改善风电的并网特性，及时准确地对其进行预测已成为风电场运营及电网调度工作亟需解决的问题。

在现有的研究中，根据预测方式的不同，风电爬坡事件可分为直接预测法和间接预测法两类。其中，直接法是指直接对爬坡率或爬坡量等爬坡信息进行预测；间接法是指首先对风电功率进行预测，然后基于预测结果提取爬坡事件的有关信息。根据预测目标的不同，风电爬坡事件预测可分为确定性预测和不确定性预测。确定性预测是指对爬坡率、爬坡持续时间等爬坡指标的值进行预测；不确定性预测是指在一定置信区间下，对爬坡率、爬坡持续时间等爬坡指标的范围进行预测。根据预测手段的不同，风电爬坡事件可分为基于NWP(数值天气预报)预测和时间序列预测。基于NWP(数值天气预报)预测是指根据风速、风向等气象信息与风电爬坡事件之间的映射关系对风电爬坡事件进行预测；时间序列预测是指基于历史爬坡信息的内在规律对未来爬坡事件进行预测。

在以上各类预测方法中存在一个共同的问题：风电爬坡事件预测的全面性与准确性无法同时满足。对风电爬坡事件预测得越全面，在所预测的爬坡事件中错误率就越高；相反，对风电爬坡事件预测得越准确，遗漏的爬坡事件就越多。针对以上问题，本发明提出一种预测策略：将风电功率爬坡量分解为若干子信号，对每个子信号分别进行预测。一方面，在每个子信号的预测过程中，在满足设定捕获率的前提下，均以最高准确率为目标；另一方面，只要其中一个子信号的预测值超过设定阈值，就认为有风电爬坡事件发生。该策略解决了风电爬坡事件预测的全面性与准确性不能兼顾的问题，对电力系统运行调度具有重要意义。

技术实现要素：

本发明要解决的技术问题在于，针对现有技术对风电爬坡事件预测的全面性与准确性不能同时满足的问题。为解决二者之间的矛盾，提供一种风电场输出功率爬坡事件的预测方法及系统。通过将原始风电爬坡序列分解为若干子信号，对子信号分别预测，根据子信号预测信息共同判定未来爬坡事件的发生情况。

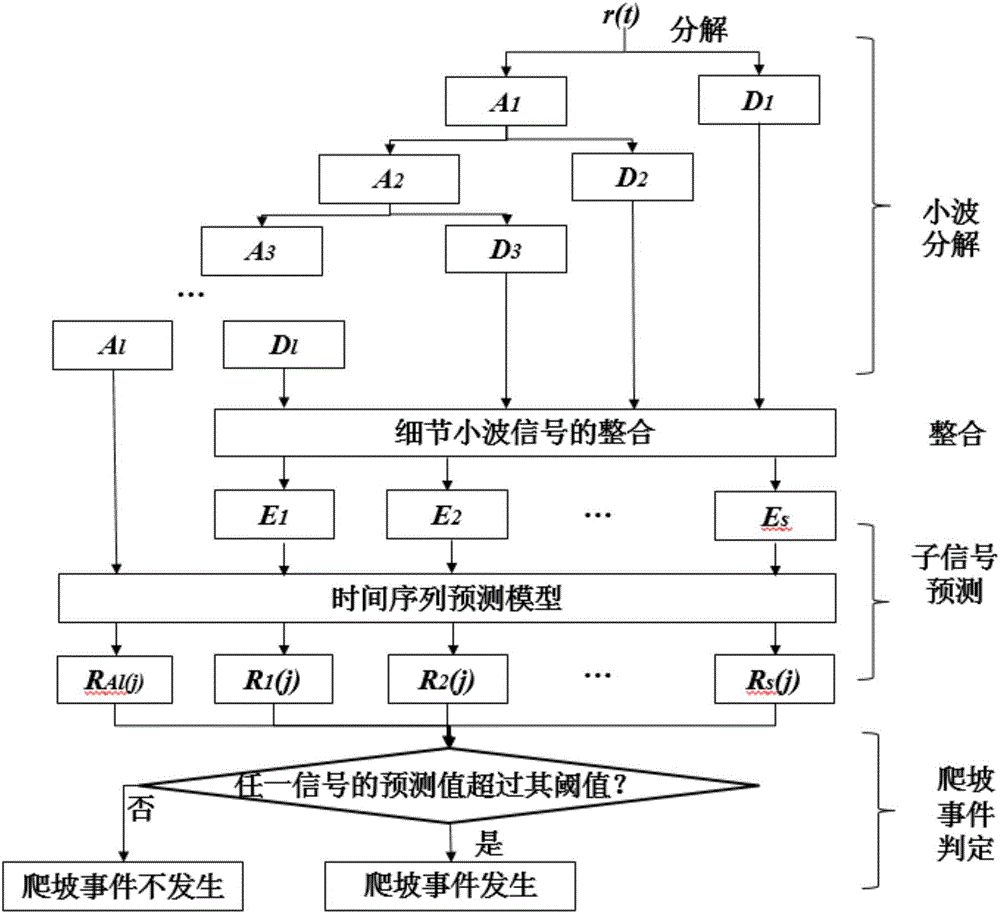
本发明提出了一种风电场输出功率爬坡事件的预测系统，其特征在于，该系统由四个主要模块构成：数据预处理模块、小波变换模块、子信号预测模块及爬坡事件判定模块；其中，数据预处理模块包括：数据读取模块和爬坡序列计算模块；小波变换模块包括：小波分解模块和子小波信号整合模块；子信号预测模块包括：时间序列预测模块和分辨率转换模块。在本系统中数据预处理模块作为小波变换模块的输入，小波变换模块的输出连接到子信号预测模块，子信号预测模块作为爬坡事件判定模块的输入。

需要说明的是，以上各模块之间的连接关系表示逻辑上的连接，而不仅限于物理上的连接。

所述数据预处理模块用于风电功率信息的提取、验证和订正，以及输出功率爬坡量序列的计算。数据预处理模块由数据读取模块和爬坡序列计算模块两部分构成。

所述数据读取模块用于提取风电功率信息，以及对原始数据进行验证和订正；

所述爬坡序列计算模块是依据数据读取模块中得到的风电功率序列，计算风电功率爬坡序列，作为样本时间序列。

所述小波变换模块用于将数据预处理模块得到的原始风电功率爬坡序列转换为若干子信号的时间序列。小波变换模块由小波分解模块和子小波信号整合模块构成。

所述小波分解模块基于小波变换技术，将数据预处理模块得到的原始风电功率爬坡序列进行l层分解，得到l+1个子信号(包含1个大约信号和l个细节信号)；

所述子小波信号整合模块用于将小波分解模块得到的l个信号重构为s个新的细节信号，由此将小波分解模块得到的l+1个子信号整合为s+1个新的子信号：E₁(t)，E₂(t)…E_s(t)及A_l(t)(s≤l)。其整合方式可根据具体案例选定，例如，将l个细节信号重构为一个信号L(s＝1)，由此将原始风电功率爬坡序列整合为2个新的子信号(一个大约信号和一个总细节信号)。

所述子信号预测模块用于对小波变换模块得到的子信号进行预测，由时间序列预测模块和分辨率转换模块构成。

所述时间序列预测模块对小波变换模块中得到的s+1个子信号(E₁(t)，E₂(t)…E_s(t)及A_l(t))分别进行时间序列预测，即基于时间序列预测模型依据其历史值预测其未来值，时间序列预测模型包括：自回归模型AR，滑动平均模型MA，自回归滑动平均模型ARMA，有外源输入的自回归滑动平均模型ARMAX，求和自回归滑动平均模型ARIMA，马尔科夫模型，混沌时间序列模型，门限自回归模型TAR，向量自回归模型VAR，自回归条件异方差模型ARCH，广义自回归条件异方差模型GARCH，均值广义自回归条件异方差模型GARCH-M，分整型广义自回归条件异方差模型FIGARCH，分整自回归移动平均模型ARFIMA。其预测原则是，在满足设定的捕获率下，追求其最大准确率；

所述分辨率转换模块用于将时间序列预测模块得到的各子信号的预测序列通过求每相邻n个预测值的最大值的方式，转化为n倍时间间隔的新时间序列；

所述爬坡事件判定模块是依据子信号预测模块得到的各自信号的预测信息对未来爬坡事件的发生情况进行判定。其判定方式如下，若超过一个子信号的预测值在时刻t超过其设定阈值，则认为在t时刻有爬坡事件发生。

一种风电场输出电功率爬坡事件预测方法，其特征在于，它包括以下步骤：

步骤1：提取风电场的实测历史输出功率数据，对原始数据进行验证和订正。并计算输出功率爬坡量序列，作为样本时间序列。

步骤2：基于小波变换原理，对输出功率爬坡量序列进行l层分解，分解的子信号包含1个近似信号(A_l)和l个细节信号(D₁，D₂，…，D_l)。然后，对l个细节信号(D₁，D₂，…，D_l)重构为s个新的子信号，于是共得到s+1个新的子信号：E₁(t)，E₂(t)…E_s(t)及A_l(t)(s≤l)；

步骤3：选择一个或几个时间序列预测模型，以最大准确率为目标分别对s+1个子信号分别进行预测，并将预测爬坡序列转换为更长时间间隔(更小时间分辨率)的新的时间序列。时间序列预测模型包括：自回归模型AR，滑动平均模型MA，自回归滑动平均模型ARMA，有外源输入的自回归滑动平均模型ARMAX，求和自回归滑动平均模型ARIMA，马尔科夫模型，混沌时间序列模型，门限自回归模型TAR，向量自回归模型VAR，自回归条件异方差模型ARCH，广义自回归条件异方差模型GARCH，均值广义自回归条件异方差模型GARCH-M，分整型广义自回归条件异方差模型FIGARCH，分整自回归移动平均模型ARFIMA；

步骤4：根据步骤3得到的s+1个子信号的预测结果，对未来风电爬坡事件进行判定。

所述步骤1的具体步骤为：

步骤101：对原始风电功率数据进行验证和订正。

数据验证是指提取数据信息，去除漏测的数据；数据订正是指利用代数差值法对挑选出来的数据进行订正，形成等时间步长的时间序列，具体方法如下：

以实测的风电场输出功率p为例，

其中，t为待订正的数据点，p(t)为修正后的风电场输出功率，t₁为待订正点前相邻最近的有效数据观测点，t₂为待订正点后相邻最近的有效数据观测点，且t₁<t<t₂，p(t₁)为t₁对应的风电场输出功率的实测值，p(t₂)为t₂对应的风电场输出功率的实测值。

步骤102：基于订正后的历史功率数据，计算输出功率爬坡量序列。

r(t)＝p(t+Δt)-p(t) (2)

式中，p(t+Δt)和p(t)分别为t+Δt和t时刻订正后的风电场输出功率，Δt为某一固定的时间间隔，r(t)为时刻t风电功率的爬坡量。

所述步骤2的具体步骤为：

步骤201：原始风电功率爬坡序列的小波分解。

通过小波变换对原始输出功率爬坡量序列进行l层分解，分解的子信号包含一个近似信号(A_l)和l个细节信号(D₁，D₂，…，D_l)。

步骤202：对l个细节信号(D₁，D₂，…，D_l)重构为s个新的信号。于是，将步骤201中得到的l+1个子信号整合为s+1个新的子信号：E₁(t)，E₂(t)…E_s(t)及A_l(t)(s≤l)，重构方式可根据具体案例选定。

所述步骤3的具体步骤为：

步骤301：选取个或几个合适的时间序列预测模型，以最大爬坡事件预测准确率FA为目标，对s+1个子信号分别进行时间序列预测。时间序列预测模型包括：如自回归模型AR，滑动平均模型MA，自回归滑动平均模型ARMA，有外源输入的自回归滑动平均模型ARMAX，求和自回归滑动平均模型ARIMA，马尔科夫模型，混沌时间序列模型，门限自回归模型TAR，向量自回归模型VAR，自回归条件异方差模型ARCH，广义自回归条件异方差模型GARCH，均值广义自回归条件异方差模型GARCH-M，分整型广义自回归条件异方差模型FIGARCH，分整自回归移动平均模型ARFIMA。其中，爬坡事件预测准确率FA、爬坡事件捕获率RC及爬坡事件预测综合指数CSI的定义式分别为：

爬坡事件捕获率：

爬坡事件捕获正确率：

爬坡事件综合

其中，

TF(正确预测个数)：同时被预测且被观察到的风电爬坡事件个数。

FF(错误预测个数)：被预测但未被观察到的风电爬坡事件个数。

MR(遗漏预测个数)：被观察但未被预测到的风电爬坡事件个数。

通过以上定义可见，RC与FA分别体现风电爬坡事件预测的全面性和准确性。所以，二者基本成负相关关系；即RC值越大，FA越小，反之亦然。在对子信号的时间序列预测模型进行训练的过程中，在其RC值满足设定条件的前提下，均以最大FA值为训练目标，确定其各自的预测模型参数。

步骤302：根据预测要求的时间分辨率，计算各个子信号在每n个连续时间点的预测值的最大值，构成新的时间序列R₁(j)，R₂(j)…R_s(j)及

$R_{A_l}\left(j\right)=max\left(\right|A_l\left(t\right)\left|\right)---\left(6\right)$

R_i(j)＝max(|E_i(t)|) (7)

式中，t＝n×(j-1)+1,n×(j-1)+1,...,n×j；i＝1,2，…s；j为正整数。

所述步骤4的具体步骤为：

基于步骤302中得到的时间序列R₁(j)，R₂(j)…R_s(j)及对未来是否风电爬坡事件进行判断。判断的原则为，只要R₁(j)，R₂(j)…R_s(j)及中有一者超过设定阈值，则判定有风电爬坡事件发生。

Y(t)为1时认为风电爬坡事件在t时刻发生，当Y(t)为0时认为风电爬坡事件在t时刻不发生。其中，i＝1,2，…s；T_r(i)及T_r(A_l)的计算方式如下：

$T_r\left(i\right)=P_r\&times;\frac{\underset{t=1}{\mathrm{\&Sigma;}}\left|E_i\left(t\right)\right|}{\underset{t=1}{\mathrm{\&Sigma;}}\left|A_l\left(t\right)\right|+\underset{i=1}{\overset{s}{\mathrm{\&Sigma;}}}\underset{t=1}{\mathrm{\&Sigma;}}\left|E_i\left(t\right)\right|}---\left(9\right)$

$T_r\left(A_l\right)=P_r\&times;\frac{\underset{t=1}{\mathrm{\&Sigma;}}\left|A_l\left(t\right)\right|}{\underset{t=1}{\mathrm{\&Sigma;}}\left|A_l\left(t\right)\right|+\underset{i=1}{\overset{s}{\mathrm{\&Sigma;}}}\underset{t=1}{\mathrm{\&Sigma;}}\left|E_i\left(t\right)\right|}---\left(10\right)$

式中，P_r为风电场装机容量的某一百分比，其值并没有统一的定义，可以根据具体风电场的情况而定。

有益效果

1.同时实现了对风电爬坡事件预测的高捕获率和高准确性

风电爬坡事件的捕获率和准确率呈负相关关系，即更高的捕获率对应更小的准确率。但本通过对风电功率爬坡量序列进行小波分解，对其子信号分别进行预测，通过子信号的预测信息对未来爬坡事件进行预测。一方面，一旦某一子信号预测出爬坡信息，则判定爬坡事件发生；另一方面，在每一子信号预测过程中以最大准确率为原则。从而实现了风电爬坡事件预测全面性与准确性的兼顾。

2.提供了一种简便易行的风电爬坡事件预测方法，

该系统基于历史风电功率数据，无需风速、风向等气象要素的输入，克服了数值天气预报误差对风电爬坡事件预测结果的影响。且该系统逻辑简单，计算量小，运算时间短。

附图说明

图1为本发明提出的风电场输出功率爬坡事件预测系统框图；

图2为本发明提出的风电场输出功率爬坡事件预测的方法流程图。

图3为本发明方法在实施例1中的流程图。

具体实施方式

本发明提供一种风电场输出功率爬坡事件预测的方法及系统，以下结合附图和具体实施例对本发明详细说明。

图1为本发明提出的一种风电场输出电功率爬坡事件预测方法的系统框图；该系统由四个主要模块构成：数据预处理模块、小波变换模块、子信号预测模块及爬坡事件判定模块；其中，数据预处理模块包括：数据读取模块和爬坡序列计算模块；小波变换模块包括：小波分解模块和子小波信号整合模块；子信号预测模块包括：时间序列预测模块和分辨率转换模块。在本系统中数据预处理模块作为小波变换模块的输入，小波变换模块的输出连接到子信号预测模块，子信号预测模块作为爬坡事件判定模块的输入。

需要说明的是，以上各模块之间的连接关系表示逻辑上的连接，而不仅限于物理上的连接。

图2为本发明提出的风电场输出功率爬坡事件预测的方法流程图，该方法流程以图1所示的系统结构为基础。以下结合第一实施例对该方法的具体过程进行详细说明，图3为本发明方法在实施例1中的流程图。

步骤1：提取中国某风电场长达一年的10分钟间隔的实测输出功率数据，对原始数据进行验证和订正，并计算输出功率爬坡量序列作为样本时间序列。

步骤2：基于小波变换原理，对输出功率爬坡量序列进行3层分解，分解的子信号包含1个近似信号A_l(t)和3个细节信号：D₁(t)，D₂(t)，和D₃(t)。然后，对3个细节信号D₁(t)，D₂(t)，和D₃(t)重构为1个新的子信号E₁(t)，于是共得到两个新的子信号：E₁(t)和A_l(t)；

步骤3：基于ARMA(自回归滑动平均)预测模型，以最大准确率为目标分别对两个子信号分别进行提前1小时的预测，并将以10分钟为间隔的爬坡预测序列转换为更长时间间隔(1小时，3小时和6小时)的新序列；

步骤4：根据步骤3得到的两个子信号的预测结果，对未来风电爬坡事件进行判定。

所述步骤1的具体步骤为：

步骤101：对原始风电功率数据进行验证和订正。

数据验证是指提取数据信息，去除漏测的数据；数据订正是指利用代数差值法对挑选出来的数据进行订正，形成等时间步长的时间序列，具体方法如下：

以实测的风电场输出功率p为例，

其中，t为待订正的数据点，p(t)为修正后的风电场输出功率，t₁为待订正点前相邻最近的有效数据观测点，t₂为待订正点后相邻最近的有效数据观测点，且t₁<t<t₂，p(t₁)为t₁对应的风电场输出功率的实测值，p(t₂)为t₂对应的风电场输出功率的实测值。

步骤102：基于订正后的历史功率数据，计算每30分钟间隔的输出功率爬坡量序列。

r(t)＝p(t+Δt)-p(t) (12)

式中，p(t+Δt)和p(t)分别为t+Δt和t时刻订正后的风电场输出功率，r(t)为时刻t风电功率的爬坡量，Δt为30分钟。

所述步骤2的具体步骤为：

步骤201：原始风电功率爬坡序列的小波分解。

通过小波变换对原始输出功率爬坡量序列进行3层分解，分解的子信号包含一个近似信号A_l(t)和3个细节信号:D₁(t)，D₂(t)，和D₃(t)。

步骤202：对3个细节信号D₁(t)，D₂(t)，和D₃(t)中重构为一个信号E₁(t)。于是，将步骤201中得到的4个子信号整合为2个新的子信号：E₁(t)及A_l(t)。

E₁(t)＝D₁(t)+D₂(t)+D₃(t) (13)

所述步骤3的具体步骤为：

步骤301：基于ARMA(自回归滑动平均)模型，以最大爬坡事件预测准确率FA为目标，对两个子信号分别进行提前1小时的预测。其中，爬坡事件预测准确率FA、爬坡事件捕获率RC及爬坡事件预测综合指数CSI的定义式分别为：

爬坡事件捕获率：

爬坡事件预测准确率：

爬坡事件综合指数：

其中，

TF(正确预测个数)：同时被预测且被观察到的风电爬坡事件个数。

FF(错误预测个数)：被预测但未被观察到的风电爬坡事件个数。

MR(遗漏预测个数)：被观察但未被预测到的风电爬坡事件个数。

通过以上定义可见，RC与FA分别体现风电爬坡事件预测的全面性和准确性。所以，二者基本成负相关关系；即RC值越大，FA越小，反之亦然。在对子信号A_l和D的时间序列预测模型进行训练的过程中，在其RC值满足设定条件的前提下，均以最大FA值为训练目标，确定其各自的预测模型参数。

经训练发现，对于提前1小时(6×10分钟＝60分钟)的风电爬坡事件预测，以前8个历史风电功率爬坡量为输入时(8×10分钟＝80分钟)，预测效果最优。

步骤302：分别计算每1小时、3小时及6小时中的最大预测爬坡量序列和R₁(j)。

根据预测要求的时间分辨率，计算对应时间段内s+1个子信号每n个预测值的最大值，构成新的时间序列R₁(j)及

$R_{A_l}\left(j\right)=max\left(\right|A_l\left(t\right)\left|\right)---\left(17\right)$

R_i(j)＝max(|E_i(t)|) (18)

式中，t＝n×(j-1)+1,n×(j-1)+1,...,n×j；j为正整数；在1小时、3小时和6小时的时间分辨率下，n分别为6(1×60/10＝18)，18(3×60/10＝18)，及36(6×60/10＝36)。

所述步骤4的具体步骤为：

基于步骤302中得到的时间序列R₁(j)，R₂(j)…R_s(j)及对未来是否风电爬坡事件进行判断。判断的原则为，只要R₁(j)，R₂(j)…R_s(j)及中有一者超过设定阈值，则判定有风电爬坡事件发生。

Y(t)为1时认为风电爬坡事件在t时刻发生，当Y(t)为0时认为风电爬坡事件在t时刻不发生。其中，i＝1,2，…s；T_r(i)及T_r(A_l)的计算方式如下：

$T_r\left(i\right)=P_r\&times;\frac{\underset{t=1}{\mathrm{\&Sigma;}}\left|E_i\left(t\right)\right|}{\underset{t=1}{\mathrm{\&Sigma;}}\left|A_l\left(t\right)\right|+\underset{i=1}{\overset{s}{\mathrm{\&Sigma;}}}\underset{t=1}{\mathrm{\&Sigma;}}\left|E_i\left(t\right)\right|}---\left(20\right)$

$T_r\left(A_l\right)=P_r\&times;\frac{\underset{t=1}{\mathrm{\&Sigma;}}\left|A_l\left(t\right)\right|}{\underset{t=1}{\mathrm{\&Sigma;}}\left|A_l\left(t\right)\right|+\underset{i=1}{\overset{s}{\mathrm{\&Sigma;}}}\underset{t=1}{\mathrm{\&Sigma;}}\left|E_i\left(t\right)\right|}---\left(21\right)$

式中，P_r为风电场装机容量的某一百分比，在本实施例中，P_r分别取装机容量的10％和15％。

经过预测数据与实测数据的对比，其预测结果如表1所示。

表1不同时间分辨率下的风电爬坡事件预测结果

结果表明，本发明能够准确地预测未来风电场输出功率的爬坡事件，且系统运行高效、简便，具有良好的工程应用前景。