城市轨道交通换乘站高峰期客流控制方法与流程

本发明涉及城市轨道交通控制领域，尤其涉及换乘站高峰期客流控制领域。

背景技术：

地铁车站是一个由客流、设施、列车等多个部分组成的混杂系统。换乘车站与普通车站相比，客流种类除了进出站乘客和上下车乘客外，还有一大部分客流为换乘客流，相应的，换乘车站的客流行走流线也要比普通车站复杂许多。

换乘通道的宽度直接决定了其通行能力。现有的规范中给出了不同宽度下通道通行能力大小，但没有考虑行人服务水平等相关因素的影响，现有技术中大多数从行人服务水平角度对通道宽度设计分析，研究方法大都基于排队论。也有部分研究学者通过分析通道内客流集散机理，提出了换乘通道合理长度评估方法。既有的管控措施在控制的触发条件、位置、时间、怎样布设等方面缺少科学依据，这样就增加了换乘站高峰时段客流组织的难度，同时也降低了换乘站的服务和安全水平。在城市轨道交通网络化进程快速发展背景下，迫切需要对高峰时段换乘站客流控制理论展开深入研究，亟需建立一套系统的科学理论与方法，以解决换乘车站高峰期过饱和客流拥堵问题。

技术实现要素：

为了解决上述技术问题，本发明以站台客流密度最小为目标，利用控制理论建立了高峰时段换乘车站客流控制模型并求解出最优客流控制策略。具体采用如下技术方案：

(1)建立换乘站高峰期客流控制模型：

状态方程：

其中，x₁(k)、x₁(k+1)分别为上行方向在k、k+1时刻站台聚集人数，x₂(k)、x₂(k+1)分别为下行方向在k、k+1时刻站台聚集人数，u₁(k)为上行方向一个周期内流入站台的客流，u₂(k)为下行方向一个周期内流入站台的客流，α为高峰时段每个采样周期内离开站台的客流与站台聚集人数比值，β为下行方向每个 采样周期内离开站台的客流与站台聚集人数的比值,q₁(k)为上行站台的干扰客流，q₂(k)为下行站台的干扰客流；

目标函数：

其中，S₁为上行站台候车面积，S₂为下行站台候车面积；

最优控制规律：

其中，为上行方向站台的最优流入客流，为下行方向站台的最优流入客流，为上行方向站台的理想流入客流流量，为下行方向站台的理想流入客流流量，为上行方向采样时刻点的站台聚集人数，为下行方向采样时刻点的站台聚集人数，为上行方向站台的理想聚集人数，为下行方向站台的理想聚集人数，q₁、q₂为来自邻近对向站台闸机所流入到本站台的干扰客流，k₁、k₂为常数。

(2)模型求解

根据干扰客流的历史数据用小波神经网络预测算法得到预测时间段内干扰客流的预测值，并设定控制步长为K步，方法如下：

(i)确定网络结构：依据干扰客流的特性设计网络各层节点的个数为n，用来表示当前时刻的前n个时刻的干扰客流的数量；隐含层的传递函数为小波函数，输出层的节点数量为1个，表征当前时刻的干扰客流的预测结果；

(ii)小波神经网络训练：用干扰客流的历史数据进行训练，次数设计为m次。

(iii)小波神经网络测试：用训练好的网络预测的干扰客流流量，并与观测的实际干扰客流流量进行比较，检验所训练网络的准确性；

得到K步内干扰客流的预测值后，第一步：采集实际数据x(0)，利用离散线 性二次最优控制理论求解在K步内使目标函数最小的K个输入变量的值U(0)^*、U(1)^*、…、U(K-1)^*；第二步：采集实际站台客流人数x(k)，再重复第一步的过程，又得到一组U(0)^*、U(1)^*、…、U(K-1)^*；从第一步到第二步，时间步长往前推进了一步，如此一直继续下去，直到到达预先设定的预测步长为止，每次都取每一步得到的第一个预测值U(0)^*来组成最优控制序列，U(0)^*′取第一步的U(0)^*，U(1)^*′取第二步的U(0)^*，……U(K-1)^*′取第K步的U(0)^*，从而得到一组最优控制序列U(0)^*′、U(1)^*′、…U(K-1)^*′。

本发明具有如下有益效果：

(1)从控制的角度对高峰时段换乘站的各类客流进行分析，把流入站台客流作为系统输入变量，采样时刻点站台客流聚集人数作为系统状态变量，以采样时刻点站台客流密度最小为目标函数，利用离散系统线性二次最优理论建立换乘车站的客流控制模型，得到目标函数下流入客流的最佳控制序列。

(2)考虑了干扰客流影响因素下，利用MPC思想建立了换乘站的客流控制模型。采用小波神经网络求解干扰客流预测值，利用MPC思想求解有干扰客流影响因素下流入站台客流的最佳控制序列。

(3)为换乘站高峰时段的客流控制方案提供理论依据，为建立高效的客流控制管理策略提供科学依据和理论基础。

(4)将换乘车站各类客流根据行走路径不同进行分类，在对站台客流集聚过程进行详细分析的基础上，发掘短期各类客流高峰时段的客流波动规律，有利于运营管理部门根据各类客流波动规律提前做出响应，提高运营管理部门的管理决策水平。

附图说明

图1为采样周期内列车停走行为图。

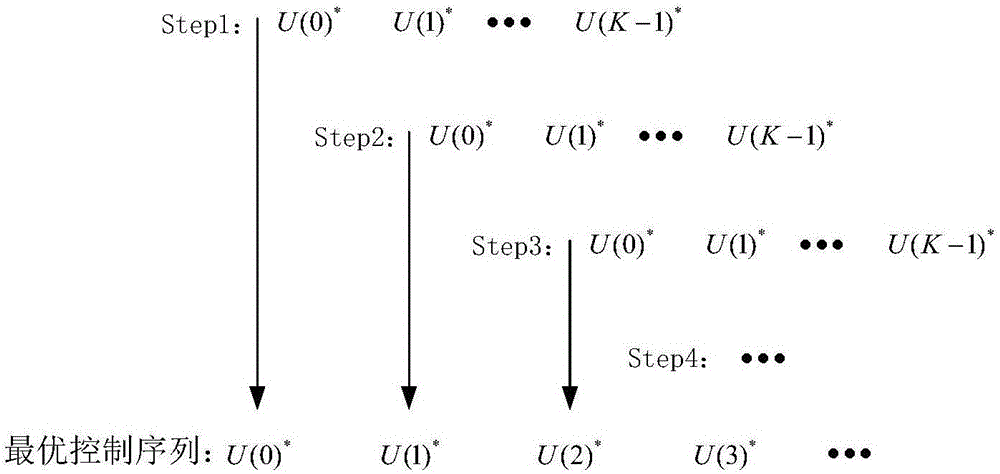
图2为MPC求解客流控制模型过程图。

具体实施方式

将两列相邻列车的发车间隔作为一个采样周期，将一个采样周期内列车的停走行为细分为列车到站(t_k)、列车停车时段(τ_sk)、列车出站(t′_k)、间隔时段 (τ_tk)四个阶段。列车在一个采样周期内的停走行为如图1所示：

设采样周期为T，由图1-2可知，一个采样周期由停车时段τ_sk和间隔时段τ_tk两部分时间段组成，即T＝τ_sk+τ_tk。其中，列车停站时段τ_sk＝t'_k-t_k，即列车从进站停车到列车再次出站的时段；间隔时段τ_tk＝t_k+1-t′_k，即从车1出站时刻到车2进站时刻之间的时间段。

对上行方向站台：设采样时刻站台聚集人数为x₁(k)，一个周期内流入站台客流为u₁(k)，高峰时段每个采样周期内离开站台的客流与站台聚集人数比值为α，S₁为上行站台候车面积，得到：

x₁(k+1)＝(1-α)x₁(k)+u₁(k)(0＜α≤1)k＝0,1,…N-1

目标函数为：

同理，可得下行方向站台客流状态方程和目标函数：

x₂(k+1)＝(1-β)x₂(k)+u₂(k)(0＜β≤1)k＝0,1,…N-1

式中，β表示下行方向每个采样周期内离开站台的客流与站台聚集人数的比值。目标函数为：

式中S₂为下行站台候车面积。

对上行下方向两个站台进行考虑，得到状态空间表达式：

得到系统目标函数为：

对应于本模型，Q和R内各元素具有实际物理意义，为适用于本模型，求解 式(4-4)中Q和R内各元素如下：

对式(4-4)中第一项：

令Q₂＝Q₃＝0，得到

对式(4-5)中第二项：

令R₁＝r₁，R₂＝R₃＝0，R₄＝r₂，得到

将Q和R代入式(4-5)得：

综上，该站客流控制的完整模型如下：

状态方程：

目标函数：

最优控制规律：

建立该模型的主要内容分为两个部分：首先利用小波神经网络求解干扰客流 的预测值，然后再利用MPC思想求解在有干扰客流因素下的最优控制序列。

1、小波神经网络求解干扰客流预测值

课题组对通过闸机流入对面站台的客流流量分别进行了现场观测，为了尽量保证预测的准确性，统计了2015年12月21至24日共4日的早高峰7:00-10:00时段的干扰客流数据，每隔3分钟计算一次该时段内干扰客流数量。上下行站台各记录240组数据流量。

以上行干扰客流预测为例，说明利用小波神经网络算法求解干扰客流预测值的流程。其流程主要分为三步：确定其网络结构、用训练数据对网络进行训练、用测试数据对网络进行测试。

(1)确定网络结构：重点是依据干扰客流的特性来设计网络各层节点的个数。本文设计输入层节点个数为4，用来表示当前时刻的前4个时刻的干扰客流的数量；隐含层的传递函数为小波函数mymorlet，该层的节点数量需要经过反复试验，根据最终预测效果的准确性来确定其数目大小。输出层的节点数量为1个，表征当前时刻的干扰客流的预测结果。

(2)小波神经网络训练：用21日至23日的3天的180个数据进行训练，次数设计为100次。

(3)小波神经网络测试：用训练好的网络预测24日的干扰客流流量，并与24日观测的实际干扰客流流量进行比较，检验所训练网络的准确性。

因为客流流量只能为整数，根据实际物理意义，按照“四舍五入”原则将预测值取整，用该算法得到在早高峰7:30-8:30时段内，上下行干扰客流预测值与观察实际值分别如表4-2、表4-3所示：

表4-2上行干扰客流预测值与实际值

表4-3下行干扰客流预测值与实际值

2、MPC求解最优控制序列

当考虑干扰客流时，每个控制步程内，上下行两个站台的状态空间表达式为：

其中，u₁'(k)＝u₁(k)+q₁(k)，u'₂(k)＝u₂(k)+q₂(k)；u₁(k)、u₂(k)表示通过闸机或换乘通道流入本站台的流入客流；q₁(k)、q₂(k)表示来自邻近对向站台闸机所流入到本站台的干扰客流。

得到最优客流控制规律为：

利用MPC控制思想建立客流控制模型的求解过程如下：

首先根据干扰客流的历史数据用小波神经网络预测算法得到预测时间段内干扰客流的预测值。设定控制步长为K步，同样以站台候车面积的客流密度最小为优化目标。第一步：得到K步内干扰客流的预测值，采集实际数据x(0)，求解在K步内使目标函数最小的K个输入变量的值U(0)^*、U(1)^*、…、U(K-1)^*。第二步：采集实际站台客流人数x(k)，再重复第一步的过程，又得到一组U(0)^*、U(1)^*、…、U(K-1)^*。从第一步到第二步，时间步长往前推进了一步，如此一直继续下去，直到到达预先设定的预测步长为止。在这个过程中，每次采集实际的站台客流人数是为了防止模型预测出现偏差，是一种反馈校正的形式。根据实际预测效果取每次控制步程的一个(或几个)输入变量的值。假设每次都取每一 步得到的第一个预测值，从而得到一组最优控制序列U(0)^*、U(1)^*、U(2)^*、…。如图2所示：

仿真中首先利用matlab的dlqr()函数求解出k₁、k₂的值，然后将k₁、k₂的值及表4-2、表4-3的值在Anylogic进行设定，在Anylogic仿真环境中编程实现MPC求解最优控制序列。