一种高炉铁水硅含量在线估计方法及系统与流程

本发明属于高炉控制
技术领域：
，具体是一种高炉铁水硅含量在线估计方法及系统。
背景技术：
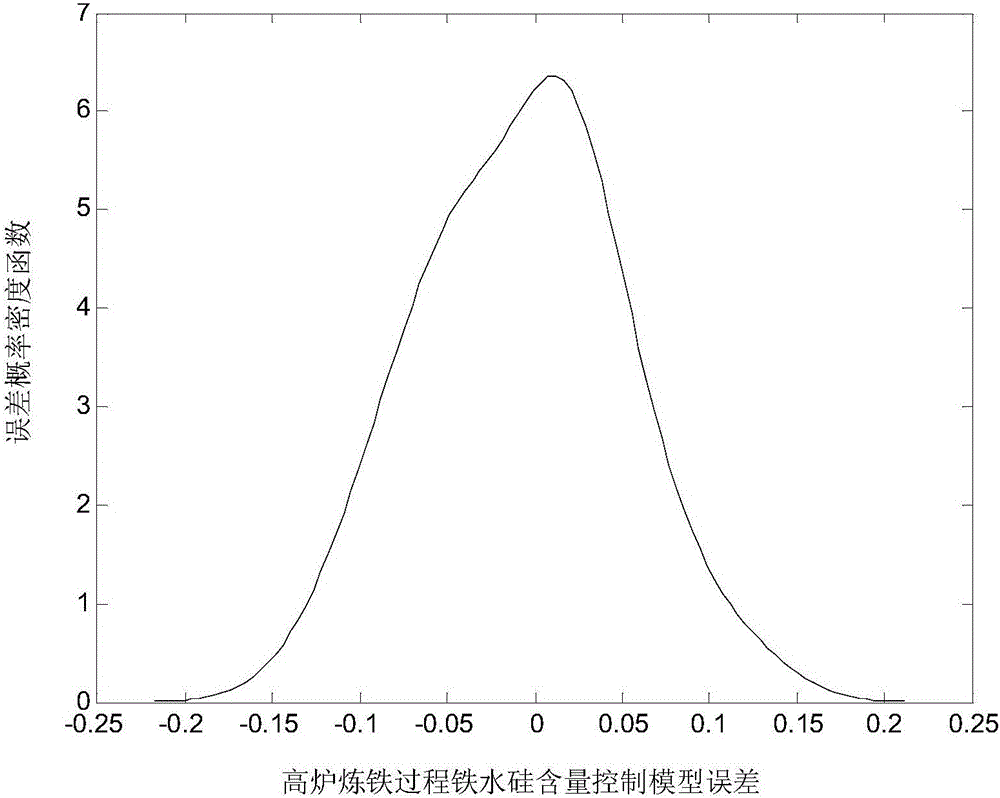
：高炉炼铁是钢铁生产中的重要单元，其作用就是将固态的铁矿石通过复杂高温、高压等物理化学变化和多相多场耦合效应，在焦炭、煤气等作用下还原成液态的铁水。目前，由于测量手段的限制，反映铁水质量和高炉热状态的关键指标——硅含量的测量一般仍采用人工定期抽样化验的方式进行，由于人工检测的滞后性和不精确性，使得基于硅含量的高炉炉况判断和高炉操作异常困难。因此，实现优质、低耗的高炉运行优化与控制就必须实现铁水硅含量的在线估计或软测量。高炉炼铁过程的上述复杂动态特性，使得用于铁水[Si]在线估计的机理模型不易建立。对于难以机理建模的复杂工业过程，数据驱动的智能建模和统计建模受到了越来越广泛的关注。在众多数据驱动建模方法中，最小二乘-支持向量机建模方法(LS-SVR)凭借其在解决小样本、非线性及高维模式识别问题中的优势，得到了广泛的应用。利用LS-SVR进行建模，需要对关键参数进行调节，以得到更小的建模误差。建模误差是一个随机变量，现有的建模方法的指标一般都是建模误差的均值和方差大小。然而，建模误差的均值和方差并不能包含误差的全部信息，只有误差概率密度函数(PDF)才能够包含误差的全部信息。技术实现要素：针对现有技术存在的不足，本发明提供一种高炉铁水硅含量在线估计方法及系统。本发明的技术方案是：一种高炉铁水硅含量在线估计方法，包括：步骤1、实时采集高炉炼铁过程中的热风压力、热风温度、富氧率、设定喷煤量、鼓风湿度、炉腹煤气量；步骤2、利用基于最小二乘-支持向量机的高炉铁水硅含量在线估计模型，在线估计高炉铁水硅含量。所述步骤2，包括：步骤2-1、建立基于最小二乘-支持向量机的高炉铁水硅含量在线估计模型，以历史高炉炼铁过程中的热风压力、热风温度、富氧率、设定喷煤量、鼓风湿度、炉腹煤气量作为输入变量，历史高炉炼铁过程中的铁水硅含量作为输出变量；步骤2-2、对高炉铁水硅含量在线估计模型进行优化，确定高炉铁水硅含量在线估计模型参数，进而确定优化后的高炉铁水硅含量在线估计模型；步骤2-3、利用优化后的高炉铁水硅含量在线估计模型，在线估计高炉铁水硅含量。所述步骤2-2，包括：步骤2-2-1、将高炉铁水硅含量在线估计模型误差转换成误差概率密度函数形式；步骤2-2-2、确定当前高炉铁水硅含量在线估计模型的误差概率密度函数和设定的理想误差概率密度函数相同时的高炉铁水硅含量在线估计模型参数，进而得到优化后的高炉铁水硅含量在线估计模型。所述步骤2-2-2，包括：步骤2-2-2-1、利用基函数分别将当前高炉铁水硅含量在线估计模型的误差概率密度函数和设定的理想误差概率密度函数解耦转换成基函数对应的权值向量，即当前的误差权值向量、理想误差权值向量；步骤2-2-2-2、将高炉铁水硅含量在线估计模型参数作为输入，当前的误差权值向量作为输出，利用子空间建模方法建立参数-权值模型，用来描述高炉铁水硅含量在线估计模型参数与当前的误差权值向量之间的函数关系；步骤2-2-2-3、利用迭代学习控制方法调节参数-权值模型输入，将参数-权值模型输出控制到理想状态，即参数-权值模型的误差权值向量与理想误差权值向量相同；步骤2-2-2-4、根据参数-权值模型的误差权值向量与理想误差权值向量相同状态下的高炉铁水硅含量在线估计模型参数，确定优化后的高炉铁水硅含量在线估计模型。一种高炉铁水硅含量在线估计系统，包括：采集模块，用于实时采集高炉炼铁过程中的热风压力、热风温度、富氧率、设定喷煤量、鼓风湿度、炉腹煤气量；估计模块，用于利用基于最小二乘-支持向量机的高炉铁水硅含量在线估计模型，在线估计高炉铁水硅含量。所述估计模块，包括：模型建立模块，用于建立基于最小二乘-支持向量机的高炉铁水硅含量在线估计模型，以历史高炉炼铁过程中的热风压力、热风温度、富氧率、设定喷煤量、鼓风湿度、炉腹煤气量作为输入变量，历史高炉炼铁过程中的铁水硅含量作为输出变量；模型优化模块，用于对高炉铁水硅含量在线估计模型进行优化，确定高炉铁水硅含量在线估计模型参数，进而确定优化后的高炉铁水硅含量在线估计模型；在线估计模块，用于利用优化后的高炉铁水硅含量在线估计模型，在线估计高炉铁水硅含量。所述模型优化模块，包括：转换模块，用于将高炉铁水硅含量在线估计模型误差转换成误差概率密度函数形式；优化模型确定模块，用于确定当前高炉铁水硅含量在线估计模型的误差概率密度函数和设定的理想误差概率密度函数相同时的高炉铁水硅含量在线估计模型参数，进而得到优化后的高炉铁水硅含量在线估计模型。所述优化模型确定模块，包括：解耦转换模块，用于利用基函数分别将当前高炉铁水硅含量在线估计模型的误差概率密度函数和设定的理想误差概率密度函数解耦转换成基函数对应的权值向量，即当前的误差权值向量、理想误差权值向量；参数-权值模型建立模块，用于将高炉铁水硅含量在线估计模型参数作为输入，当前的误差权值向量作为输出，利用子空间建模方法建立参数-权值模型，用来描述高炉铁水硅含量在线估计模型参数与当前的误差权值向量之间的函数关系；迭代学习模块，用于利用迭代学习控制方法调节参数-权值模型输入，将参数-权值模型输出控制到理想状态，即参数-权值模型的误差权值向量与理想误差权值向量相同；优化模型输出模块，用于根据参数-权值模型的误差权值向量与理想误差权值向量相同状态下的高炉铁水硅含量在线估计模型参数，确定优化后的高炉铁水硅含量在线估计模型。有益效果：本发明利用最小二乘-支持向量机对高炉铁水硅含量进行建模，并直接从模型误差概率密度函数曲线入手，利用随机分布控制理论将建模误差概率密度函数曲线解耦为更容易控制的误差权值向量，通过改变高炉铁水硅含量在线估计模型参数，即正则化参数c和高斯核函数伸缩量σ来控制建模误差PDF曲线的形状，使高炉铁水硅含量在线估计模型的误差概率密度函数曲线达到理想状态，取得了良好建模，利用优化的高炉铁水硅含量在线估计模型对高炉铁水硅含量在线估计，得到了准确的估计结果。附图说明图1为本发明具体实施方式中高炉铁水硅含量在线估计方法流程图；图2为本发明具体实施方式中当正则化参数c＝30高斯核函数神缩量σ＝10时得到的误差概率密度函数曲线；图3为本发明具体实施方式中利用迭代学习控制得到的最后一个迭代周期的误差权值向量图；图4为本发明具体实施方式中选取的二次型性能指标与迭代学习次数的关系图；图5为本发明具体实施方式中利用迭代学习控制得到的最后一个迭代周期的高炉铁水硅含量在线估计模型的误差密度函数曲线图；图6为本发明具体实施方式中利用迭代学习控制得到的最后一次迭代所对应的误差概率密度函数曲线与理想误差概率密度函数曲线对比图；图7为本发明具体实施方式中步骤2流程图；图8为本发明具体实施方式中步骤2-2流程图；图9为本发明具体实施方式中步骤2-2-2流程图；图10为本发明具体实施方式中高炉铁水硅含量在线估计系统框图；图11为本发明具体实施方式中估计模块框图；图12为本发明具体实施方式中模型优化模块框图；图13为本发明具体实施方式中优化模型确定模块框图。具体实施方式下面结合附图对本发明的具体实施方式做详细说明。一种高炉铁水硅含量在线估计方法，如图1所示，包括：步骤1、实时采集高炉炼铁过程中的热风压力、热风温度、富氧率、设定喷煤量、鼓风湿度、炉腹煤气量；步骤2、利用基于最小二乘-支持向量机的高炉铁水硅含量在线估计模型，在线估计高炉铁水硅含量。所述步骤2，如图7所示，包括：步骤2-1、建立基于最小二乘-支持向量机(LS-SVR)的高炉铁水硅含量在线估计模型，以历史高炉炼铁过程中的热风压力x1、热风温度x2、富氧率x3、设定喷煤量x4、鼓风湿度x5、炉腹煤气量x6作为输入变量x＝[x1，x2，…，xn]，即n＝6，历史高炉炼铁过程中的铁水硅含量作为输出变量y；利用文献【VapnikVN.Anoverviewofstatisticallearningtheory[J].IEEETransNeuralNetwork.1999，10(5)：988-999】报道的LS-SVR进行建模。将不同历史时刻采集的输入变量数据训练数据集为xi∈RN，yi∈R，N为训练数据量。建立基于最小二乘-支持向量机(LS-SVR)的高炉铁水硅含量在线估计模型：式中：为训练数据在特征空间F的非线性映射，a是与特征空间相同维度的训练数据权值向量，b为偏移量，f(x)为模型输出变量值即高炉炼铁过程铁水硅含量值。基于最小二乘-支持向量机(LS-SVR)的高炉铁水硅含量在线估计模型可以描述为求解如下二次规划(QP)问题，即以高炉铁水硅含量在线估计模型的输出变量值的误差平方最小为目标的目标函数：式中：c为正则化参数，ei为高炉铁水硅含量在线估计模型误差，即高炉铁水硅含量在线估计模型输出变量值与实际高炉炼铁过程铁水硅含量的差值。为简化计算，引入拉格朗日乘子：式中：λi∈R为拉格朗日乘子。令式(3)中的各偏导数为零：消去变量a和ei，得到如下线性方程用来求解a和b：01T1Ω+c-1I·bλ=0y---(5)]]>式中：y＝(y1，y2，…，yN)T，λ＝(λ1，λ2，…，λN)T；Ω是N维方阵，是满足Mercers条件的核函数。本实施方式选用如下径向高斯核函数K(x,xi)=exp(||x-xi||2σ2)---(6)]]>式中：σ为高斯函数伸缩量。上述线性方程中c和σ为给定参数，因此下面针对这两个参数进行优化，从而确定最佳的a和b，进而确定最终的高炉铁水硅含量在线估计模型。步骤2-2、对高炉铁水硅含量在线估计模型进行优化，确定高炉铁水硅含量在线估计模型参数，进而确定优化后的高炉铁水硅含量在线估计模型；所述步骤2-2，如图8所示，包括：步骤2-2-1、将高炉铁水硅含量在线估计模型误差转换成误差概率密度函数形式；选择正则化参数c＝1∶1∶30(30组)，高斯核函数伸缩量σ＝1∶0.5∶9(7组)，共270组高炉铁水硅含量在线估计模型误差，通过统计，得到出在不同范围内误差的所占百分比，即误差的分布情况，由此可以得到270组误差概率密度函数(PDF)曲线。当正则化参数c＝30，高斯核函数神缩量σ＝10时得到的误差概率密度函数(PDF)曲线如图2所示。步骤2-2-2、确定当前高炉铁水硅含量在线估计模型的误差概率密度函数和设定的理想误差概率密度函数相同时的高炉铁水硅含量在线估计模型参数，进而得到优化后的高炉铁水硅含量在线估计模型。所述步骤2-2-2，如图9所示，包括：步骤2-2-2-1、利用基函数分别将当前高炉铁水硅含量在线估计模型的误差概率密度函数和设定的理想误差概率密度函数解耦转换成基函数对应的权值向量，即当前的误差权值向量、理想误差权值向量；采用文献【WangH.BoundedDynamicStochasticSystems[M].SpringerLondonLtd，2000.】报道的随机分布控制理论B样条逼近方法，将270组误差概率密度函数(PDF)曲线转化为基函数对应的权值向量。误差概率密度函数(PDF)曲线表达式为γ(y)，用平方根B样条模型逼近误差概率密度函数(PDF)曲线的平方根，在离散系统中无误差逼近的条件为：γ(y)=Σi=1nωiBi(y)---(7)]]>式中：ωi为基函数对应的权值向量，Bi(y)为B样条基函数，共有n个基函数，基函数可由以下递推公式得到：Bi,1(y)=1y∈[yi,yi+1)0y∉[yi,yi+1)---(8)]]>Bi,k(y)=y-yiyi+k-1-yiBi,k-1(y)+yi+k-yyi+k-yi+1Bi+1,k-1(y)---(9)]]>式中：Bi，k表示在高炉铁水硅含量在线估计模型的误差分布区间[yi，yi+1)上的阶数为k的第i个基函数。在本实施方式中，取阶数k＝3。提取误差概率密度函数(PDF)曲线对应的权值向量：将误差概率密度函数(PDF)曲线表达如下：γ(y)=C0(y)Vk+wn,kBn(y)=[C0(y)Bn(y)]Vkwn,k---(10)]]>式中：Vk＝[w1，w2，…，wn-1]表示k时刻的前n-1个基函数对应的权值向量，wn，k为k时刻第n个基函数对应的权值向量，C0(y)＝[B1(y)B2(y)…Bn-1(y)]为选定的n-1个基函数。对式(10)两边同时左乘[C0(y)T，Bn(y)]，整理得到如下方程：C0(y)TBn(y)γ(y)=C0(y)TC0(y)C0(y)TBn(y)Bn(y)C0(y)Bn(y)2Vkwn,k---(11)]]>对式(11)两边同时积分得到：∫abC0(y)Tγ(y)dy∫abBn(y)γ(y)dy=Σ0Σ1TΣ1Σ2-1Vkwn,k---(12)]]>式中：将式(12)两边同时左乘得到误差权值向量的计算公式为：Vkwn,k=Σ0Σ1TΣ1Σ2-1∫abC0(y)Tγ(y)dy∫abBn(y)γ(y)dy---(13)]]>利用随机分布控制理论中的B样条逼近方法，将理想误差概率密度函数转化为理想误差权值向量：选取期望为0，方差为0.062的正态分布为理想误差概率密度函数，其表达式为：γ(y)=12π×0.06exp(-y22×0.062)---(14)]]>将式(14)代入式(13)中，得到理想误差权值向量。步骤2-2-2-2、将高炉铁水硅含量在线估计模型参数c和σ作为输入，当前的误差权值向量作为输出，利用子空间建模方法建立参数-权值模型，用来描述高炉铁水硅含量在线估计模型参数与当前的误差权值向量之间的函数关系；采用文献【VanOverschee，DeMoor.Subspaceidentificationforlinearsystems：Theoryimplementationapplications[M].Dordrecht：KluwerAcademicPublishers，1996】中报道的子空间建模方法建立参数-权值模型，其中参数-权值模型的输入输出变量如下：参数-权值模型输入：正则化参数c和高斯核函数伸缩量σ参数-权值模型输出：转化出来的270组误差权值向量；步骤2-2-2-3、利用迭代学习控制方法调节参数-权值模型输入，将参数-权值模型输出控制到理想状态，即参数-权值模型的误差权值向量与理想误差权值向量相同；利用文献【AmannN，RogersE.Itearativelearningcontrolfordiscrete-timesystemswithexponentialrateofconvergence[J].IEEProc.ControlTheoryApplication.1996，143(2)：217-224】报道的迭代学习控制理论，将270组误差权值向量控制到理想状态；参数-权值模型如下：αi+1,k=Aαi,k+Bui,kVi,k=Cαi,k+Dui,k---(15)]]>式中：α∈Rn，u∈Rm，V∈Rp，分别为参数-权值模型的状态变量、参数-权值模型输入、参数-权值模型输出，k代表迭代周期数，k∈[0，1，2…N]，i代表采样点数。设在整个运行过程中时间域被分为80个迭代周期，每个迭代周期共有10个采样点，即N＝80。由式(15)可以得到第k个迭代周期中的i个采样点的误差权值向量逼近为Vi，k＝V0+Gui，k(16)式中：Vi，k为第k个迭代周期第i个采样点的误差权值向量，ui，k为第k个迭代周期第i个采样点的参数-权值模型输入，V0为初始误差权值向量。V0＝[CT，(CA)T，(CA2)T…(CAi)T]Tα0，i式中：α0，i为初始状态量。为了满足迭代学习控制的初始条件要求，同时也不失一般性，假设每个迭代周期的误差权值向量初始状态都为零。为了将基于范数优化的迭代学习控制理论应用于参数-权值模型，选取如下二次型性能指标：Jk+1(uk+1)＝||ek+1||Q2+||uk+1-uk||R2＝ek+1TQek+1+(uk+1-uk)TR(uk+1-uk)(18)式中：uk＝[u0，kT，u1，kT，u2，kT…ui，kT]T，Q和R为预先定义的正定矩阵，式中第一项||ek+1||Q2为第k次迭代周期的误差权值向量跟踪误差即ek+1＝Vk-Vg，表示第k次迭代的误差权值向量与理想误差权值向量之间的差值，式中第二项||uk+1-uk||R2表征了相邻两次迭代的参数-权值模型输入之差，是为了迭代参数-权值模型输入平稳过渡。最小化该性能指标，可以使得当前误差权值向量与理想误差权值向量最为接近，并且使得参数-权值模型输入达到平稳过渡的目的。为了保证性能指标的单调递减，根据李雅普诺夫稳定性判据，要使其导数小于零。因此对式(18)求导得到：12∂Jk+1∂uk+1=GTQek+1+R(uk+1-uk)---(19)]]>由式(19)可以看出解出的第k+1迭代的最优参数-权值模型输入uk+1是非因果的，因此考虑用第k次的迭代误差权值向量表示k+1次的迭代误差权值向量：ek+1＝ek+(Vk+1-Vg)-(Vk-Vg)＝ek+Vk+1-Vk＝ek+G(uk+1-uk)(20)式中：Vg表示为理想误差权值向量，Vk为第k次迭代的误差权值向量结果。将式(20)代入到式(19)中，得到性能指标导数值，另其小于零，可以使得性能指标单调递减，得到：12∂Jk+1∂uk+1=GTQek+[GTQG+R](uk+1-uk)<0⇒Δuk<-φk---(21)]]>式中：φk＝[GTQG+R]-1GTQek，引入自适应迭代学习率，得到：参数-权值模型输入增量Δuk(i)=-(1+β)φk(i),φk(i)>0-(1-β)φk(i),φk(i)<0---(22)]]>式中：β为自适应学习率。由式(22)得到最优迭代参数-权值模型输入为：uk+1(i)＝uk(i)+Δuk(i)(23)利用上述迭代学习率，不断更新迭代学习参数-权值模型输入，可以使性能指标逐渐减小，从而达到误差权值向量与理想误差权值向量最为接近的状态，由此，可以使得高炉铁水硅含量在线估计模型的误差概率密度函数与设定的理想误差概率密度函数最为接近。迭代结束后，可以得到最后一个迭代周期的误差权值向量，如图3所示，从图中可以看出，误差权值向量最终收敛到理想状态。迭代过程中，性能指标变化如图4所示，从图中可以看出性能指标呈指数下降状态，迭代误差最终收敛到0。迭代结束后，可以得到最后一个迭代周期的实时误差概率密度函数曲线附图5所示，从图中可以看出，误差概率密度函数曲线最终收敛到理想状态。迭代结束后，可以得到最后一次迭代对应的误差概率密度函数曲线与理想误差概率密度函数曲线如图6所示，从图中可以看出，最终迭代出来的误差概率密度函数与理想误差概率密度函数基本一样，因此，通过迭代学习控制，可以达到高炉铁水硅含量在线估计模型目标。步骤2-2-2-4、根据参数-权值模型的误差权值向量与理想误差权值向量相同状态下的高炉铁水硅含量在线估计模型参数，确定优化后的高炉铁水硅含量在线估计模型。步骤2-3、利用优化后的高炉铁水硅含量在线估计模型，在线估计高炉铁水硅含量。本实施方式还提供一种高炉铁水硅含量在线估计系统，如图10所示，包括：采集模块，用于实时采集高炉炼铁过程中的热风压力、热风温度、富氧率、设定喷煤量、鼓风湿度、炉腹煤气量；估计模块，用于利用基于最小二乘-支持向量机的高炉铁水硅含量在线估计模型，在线估计高炉铁水硅含量。所述估计模块，如图11所示，包括：模型建立模块，用于建立基于最小二乘-支持向量机的高炉铁水硅含量在线估计模型，以历史高炉炼铁过程中的热风压力、热风温度、富氧率、设定喷煤量、鼓风湿度、炉腹煤气量作为输入变量，历史高炉炼铁过程中的铁水硅含量作为输出变量；模型优化模块，用于对高炉铁水硅含量在线估计模型进行优化，确定高炉铁水硅含量在线估计模型参数，进而确定优化后的高炉铁水硅含量在线估计模型；在线估计模块，用于利用优化后的高炉铁水硅含量在线估计模型，在线估计高炉铁水硅含量。所述模型优化模块，如图12所示，包括：转换模块，用于将高炉铁水硅含量在线估计模型误差转换成误差概率密度函数形式；优化模型确定模块，用于确定当前高炉铁水硅含量在线估计模型的误差概率密度函数和设定的理想误差概率密度函数相同时的高炉铁水硅含量在线估计模型参数，进而得到优化后的高炉铁水硅含量在线估计模型。所述优化模型确定模块，如图13所示，包括：解耦转换模块，用于利用基函数分别将当前高炉铁水硅含量在线估计模型的误差概率密度函数和设定的理想误差概率密度函数解耦转换成基函数对应的权值向量，即当前的误差权值向量、理想误差权值向量；参数-权值模型建立模块，用于将高炉铁水硅含量在线估计模型参数作为输入，当前的误差权值向量作为输出，利用子空间建模方法建立参数-权值模型，用来描述高炉铁水硅含量在线估计模型参数与当前的误差权值向量之间的函数关系；迭代学习模块，用于利用迭代学习控制方法调节参数-权值模型输入，将参数-权值模型输出控制到理想状态，即参数-权值模型的误差权值向量与理想误差权值向量相同；优化模型输出模块，用于根据参数-权值模型的误差权值向量与理想误差权值向量相同状态下的高炉铁水硅含量在线估计模型参数，确定优化后的高炉铁水硅含量在线估计模型。当前第1页1 2 3