一种基于双目立体视觉系统的多视角三维重建方法与流程

本发明涉及多镜头机器视觉
技术领域：
，具体涉及一种基于双目立体视觉系统的多视角三维重建方法。
背景技术：
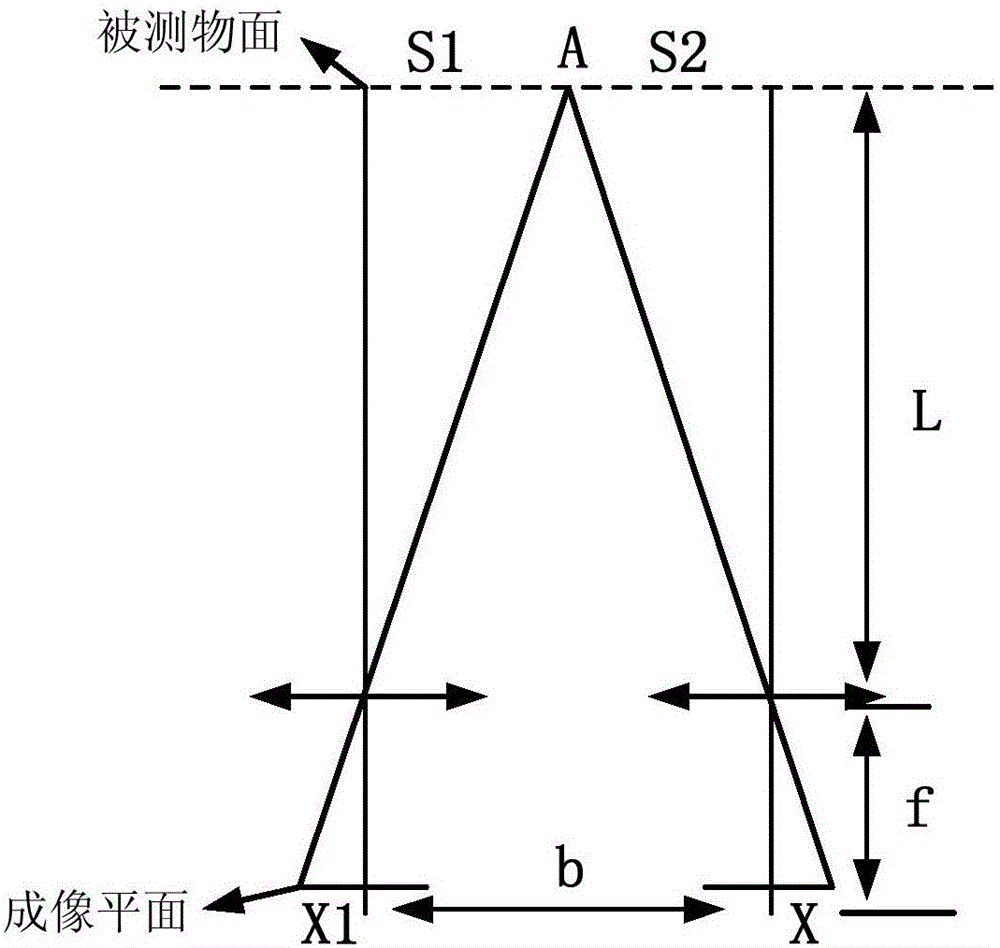
：三维重建是通过数字化手段对三维物体建立适合计算机表示和处理的数学模型。二维信息已经在众多领域有应用，但随着工业生产的要求，物体的二维信息已经不能满足于人们的要求。三维重建技术能够快速、精确的数字化表示三维物体。从而被广泛应用在工业测量、3D打印、文物数字化、人机交互等众多领域，其研究价值日益凸显。三维数据采集通常有两种方式。测量设备接触被重建物体表面测量数据。主要优点是数据采集不受物体材质和光线影响，边缘轮廓保存完整，精度较高。缺点是数据采集速度慢，效率低。另外一种设备主要利用光、声波等物理特性。例如3D扫描仪、TOF相机等。其优点是测量速度快，效率高，缺点是易受光照和物体表面材质影响，轮阔边缘保存不完整。三维重建技术能够快速、精确的数字化表示三维物体。该技术对人类生活具有重要作用。研究价值日益凸显，众多学者和公司从事相关方向的研究。2011年微软研究院开始进行一个名为KinectFusion项目，通过移动Kinect设备扫描物体进行实时三维模型重建。通过融合不同时序的深度数据，重建出目标物的三维模型，可以达到适时效果。2014年Google宣布了Tango项目，使用低成本的手机进行场景的3D扫描。其基本原理和KinectFusion相似。目前，现有的三维信息采集设备昂贵，三维重建操作相对复杂。基于双目立体视觉系统三维重建可以在相同重建效果下，大幅度降低三维信息采集设备费用，目前基于双目立体视觉系统三维重建市场应用少，具有较高的研究价值、应用价值和市场价值。技术实现要素：为了克服现有技术存在的缺陷，本发明提供一种基于双目立体视觉系统的多视角三维重建方法，该方法具有三维信息采集设备低廉、过程简单有效、工程实用价值高的优点。本发明采用如下技术方案：一种基于双目立体视觉系统的多视角三维重建方法，包括如下步骤：S1根据被重建物体大小建立双目立体视觉系统，所述双目立体视觉系统由两个型号及参数相同的摄像头构成，两个摄像头平行固定，对两个摄像头进行立体标定，制作双目立体视觉恢复三维信息查找表；S2双目立体视觉系统采集被重建物体的视频信息，对右摄像头采集的视频信息进行单应性变换，将单应性变换后的视频信息和对应左摄像头采集的视频信息进行立体匹配得到被重建物体的视差，根据视差和三维信息查找表得到图像中每个点的三维信息；S3对重建物体不同视角三点云信息进行依次进行预处理、粗配准、精配准，获取相邻视角点云之间的旋转和平移，然后将不同视角三维点云转换到同一坐标系，完成对被重建物体多视角的三维重建。所述S1根据被重建物体大小建立双目立体视觉系统，所述双目立体视觉系统由两个型号及参数相同的摄像头构成，两个摄像头平行固定，对两个摄像头进行立体标定，制作双目立体视觉恢复三维信息查找表，具体为：S1.1所述双目立体视觉系统由两个型号及参数相同的摄像头构成，两个摄像头平行固定；S1.2对左右摄像头进行标定，获取左右摄像头的光心坐标、焦距、内参、两摄像头之间的旋转和平移参数，所述两个摄像头具体左、右摄像头；S1.3然后在双目摄像头前方设置标定板，标定板与双目摄像头图像平面平行，找到对应距离的视差，根据视差与距离之间的反比例关系，导出视差和深度的查找表即Z坐标和视差之间的关系查找表；S1.4所述视差和三维坐标点之间的关系为：X＝B(X1-O1)/(X1-X2)Y＝B(Y1-O1)/(X1-X2)Z＝Bf/(X1-X2)其中，Z为物体距离双目摄像头的深度值，B为双目摄像头的基线长度，X1,X2分别是特征点在左右像素平面上的像素坐标值，f是双目摄像头的焦距，单位是像素；S1.5根据视差和三维点坐标之间的关系，可知X、Y坐标和Z坐标之间相差一个系数，由视差深度表，即可得到视差和X、Y坐标之间的查找表。所述S2中左右摄像头采集被重建物体的视频信息，对右摄像头采集的视频信息进行单应性变换，将单应性变换后的视频信息和对应左摄像头采集的视频信息进行立体匹配得到被重建物体的视差视频，根据视差视频恢复物体的三维信息，具体为：S2.1左右摄像头采集被重建物体的视频信息，所述视频信息帧率同步；S2.2对右摄像头采集的视频信息进行单应性变换，所述单应性变换包括单应性矩阵求解和图像映射插值；S2.3将单应性变换后的视频信息和对应左摄像头采集的视频信息进行立体匹配得到图像中每个点的视差，根据视差值和三维信息查找表得到图像中每个点的三维信息。所述S3中，预处理包括离散点的去除、点云的降采样及噪声的去除。预处理后的三维点云进行粗配准获取相邻视角三维点云之间的初始旋转矩阵和平移矩阵，已知相邻视角三维点云之间的初始旋转矩阵和平移矩阵进行精配准，采用ICP迭代最邻近点算法对相邻视角进行精配准，得到最优旋转矩阵和平移矩阵。所述粗配准采用基于二维RGB图辅助三维点云粗配准方案。本发明的有益效果：(1)本发明方法可以大幅度降低三维数据采集设备费用。(2)本发明方法可以实现有较大平移和旋转相邻视角的配准。(3)本发明方法简单有效，具有很高的工程实用价值。附图说明图1是本发明的工作流程图；图2是本发明实施例1中的视差深度原理图；图3是本发明实施例1中的双目立体视觉系统模型示意图；图4是本发明实施例1中的生成三维点云流程图；图5是本发明实施例1中的单应性矩阵映射图；图6是本发明实施例1中的双线性插值原理图；图7是本发明实施例1中的正向映射模型图；图8是本发明实施例1中的逆向映射模型图；图9为本发明实施例1的二维RGB图辅助三维点云粗配准的流程图；图10为本发明实施例1多视角三维点云配准流程图。具体实施方式下面结合实施例及附图，对本发明作进一步地详细说明，但本发明的实施方式不限于此。实施例一种基于双目立体视觉系统的多视角三维重建方法，包括如下步骤：如图1所示，S1根据被重建物体大小建立双目立体视觉系统，包括摄像头的选择，基线的大小设置、摄像头的分辨率设置等。所述双目立体视觉系统包括具有平行光轴结构的左、右摄像头，采用外置标准尺寸棋盘格标定法对左右摄像头进行标定，得到双目摄像头的光心坐标、焦距、畸变系数、内参、两摄像头之间的旋转和平移参数，制作双目立体视觉恢复三维信息查找表，具体为：具体如下：1.1)如图2所示的双目立体视觉系统双目相机结构示意图。双目像机采用两个型号相同、参数基本相同的摄像头，且两个摄像头保持平行并固定在云台上。水平校准仪可以校准水平，可以旋转。1.2)待测点A，深度L与在两个图像平面的视差是X＝X1+X满足反比例关系：L=b*fX---(1)]]>其中b基线长度、f为摄像头焦距、X为视差1.3)由(1.2)可知双目立体视觉系统恢复三维信息与焦距、基线、视差有关。与焦距大小、基线的长度成正比和视差大小成反比。但是基线越大、焦距越大双目立体视觉系统左右摄像头公共区域越小。分辨率越高视差值越大，但是计算量越大，运算速度越慢。因此设计双目立体视觉系统要根据项目要求综合考虑。1.4)采用外置标准尺寸棋盘格标定法对左右摄像头进行立体标定，采用工程上的常用标定算法张正友标定算法。在Matlab和Opencv都已经有现成的标定方案，可以借助标定工具箱进行标定。即可获取双目摄像头光心坐标、焦距、内参、两摄像头之间的旋转和平移参数。1.5)如图3所示平行双目立体视觉系统模型示意图。两摄像头参数基本相同。C1、C2为两摄像头的光心，光轴C1O1交图像平面X1O1Y1于点O1，光轴C2O2交图像平面X2O2Y2于点O2，左右摄像头的光轴平行。空间点P(X,Y,Z)在两图像的投影点P1(X1,Y1)和P2(X2,Y2)。C1C2为基线长度，任意一台摄像头平移基线长度可以和另一台摄像头图像平面重合。以左摄像头光心O1为坐标系原点，O1X1为X轴方向，O1Y1为Y轴方向，O1Z1为Z轴方向。双目立体视觉系统三角测量是基于视差和深度成反比的原理。双目立体视觉系统要求两台摄像头的参数性能基本相同，光轴相互平行且X轴互相重合。I1,I2为左右摄像头的图像平面，P1,P2分别为空间点P在左右图像平面上的成像点。f是摄像头的焦距,视差定义为|X1-X2|。由相似三角形可以导出视差和三维坐标点之间的关系：X＝B(X1-O1)/(X1-X2)(2)Y＝B(Y1-O1)/(X1-X2)(3)Z＝Bf/(X1-X2)(4)Z为物体距离双目摄像头的深度值，B为双目摄像头的基线长度，X1,X2分别是特征点在左右像素平面上的像素坐标值，f是双目摄像头的焦距，单位是像素。1.6)在双目摄像头前方放置一块标定板，标定板保持与双目摄像头图像平面平行。将标定板移至距离双目摄像头较远处，拍摄两张照片，进行标定求单应性矩阵。按照0.1米甚至更小的距离间隔向双目摄像头移动，拍摄一组照片。利用已求出的单应性矩阵做映射，即可得到对应距离的视差。根据视差和距离之间的反比例关系，既可用反比例关系进行拟合，导出视差深度表。由式(2)(3)(4)双目立体视觉系统恢复三维信息示意图可知X、Y坐标和Z坐标之间相差一个系数，即可得到视差和X、Y坐标之间的查找表。S2如图4所示，左右摄像头采集被重建物体的视频信息，对右摄像头采集的视频信息进行单应性变换，将单应性变换后的视频信息和对应左摄像头采集的视频信息进行立体匹配得到被重建物体的视差，根据视差和三维信息查找表得到图像中每个点的三维信息；具体为：2.1)双目立体视觉系统借助于Opencv库采集被重建物体的视频信息，确保左右摄像头采集的视频信息帧率同步。2.2)空间点在两个摄像头下的图像点具有一一对应关系，对应关系是齐次性的，可以用3阶单应性矩阵来描述。单应性矩阵中可以描述图像的平移、旋转等关系。如图5所示单应性矩阵映射图。空间平面上的三维坐标点M，在两个图像平面上的投影点为Ml和Mr。由摄像头的小孔成像模型可以知道，从空间平面到两个图像平面存在映射矩阵H1和H2使Ml＝H1X、Mr＝H2X，由于平面Π不通过摄像头的任意光心，因此在Ml和Mr之间存在射影变换变换H＝H2H'1。两图像对应点之间单应性矩阵如式所示。Mr=HM1=h1h2h3h4h5h6h7h8h9M1---(5)]]>可以利用归一化的DLT来求解单应性矩阵。2.2.1根据DLT算法求解单应性矩阵求解步骤，需要在成像平面上至少选取4组对应点。首先给对应点做归一化处理，将对应点坐标减去均值除以标准差，可归一化到Ml＝TLM(6)Mr＝TrM(7)2.2.2对于两对应点X'i和Xi有X'i＝HXi，又由两向量叉乘为0的性质可以得到。如果H矩阵第j行可以表示为hjT，那HXi可以表示为HXi=h1TXih2TXih3TXi---(8)]]>若X'i＝(X'i,Y′i,Z'i)T,那么叉乘可以表示为：Xi′×HXi=yi′h3Txi-wi′h2Txiwi′h1Txi-xi′h3Txixi′h2Txi-yi′h1Txi---(9)]]>由于，因此上式可以表示为:0T-wi′xiTyi′xiTwi′xiT0T-xi′xiT-yi′xiTxi′xiT0Th1h2h3=0---(10)]]>h1h2h3=H=h1h2h3h4h5h6h7h8h9---(11)]]>将归一化的点坐标组成上述3n×9的矩阵，为了减少计算过程可以可以简化成2n×9的矩阵。2.2.3对上述2n×9矩阵进行SVD奇异值分解求解H矩阵。2.3图像映射插值技术包括像素坐标计算和像素插值技术。工程上常用像素插值技术是双线性插值、双三次插值。如图6所示双线性插值原理图，Q11,Q12,Q21,Q22分别为四个顶点的值。首先在X方向上进行插值，可以得到：R1=x2-xx2-x1Q11+x-x1x2-x1Q21---(12)]]>R2=x2-xx2-x1Q12+x-x1x2-x1Q22---(13)]]>然后在Y方向上进行插值，可以得到：P=y2-yy2-y1R1+y-y1y2-y1R2---(14)]]>像素坐标计算有两种映射模型，正向坐标映射模型和逆向坐标映射模型。如图7所示正向映射模型、如图8所示逆向映射模型。使用正向坐标映射模型实现会出现像素缺少，同时双线性插值工程实现更为复杂，因此采用逆向坐标映射，双线性插值技术工程实现简单，不会出现像素缺少现象。2.4)立体匹配的目的是得到图像中每个点的视差，根据视差值查找视差和三维信息的查找表，可以得到图像中每个点的三维信息，因此采用基于模块的匹配方式。2.5)由式(2)(3)(4)，双目立体视觉系统三角测量是基于视差和深度成反比的原理，由相似三角形可以导出视差和三维坐标点Z坐标之间的查找表。S3根据物体的三维信息，对三维点云进行依次进行预处理、粗配准、精配准，将不同视角三维点云转换到同一坐标系，完成对被重建物体多视角的三维重建。3.1)根据三维点云的质量选择点云预处理的方式。离散点去除和噪声去除可以提高三维重建质量，点云的降采样可以减少计算机的运算量，提高重建的速度。3.2)三维点云的粗配准是获取相邻视角点云之间的初始旋转矩阵和平移矩阵，本方案提出基于二维RGB图辅助三维点云粗配准方案。如图9所示二维RGB图辅助三维点云粗配准的流程图。借助于不同视角下深度图对应的二维RGB图像进行粗配准，对RGB图像特征点检测、特征点描述、目标特征点集匹配、消除错误匹配点。根据匹配点对查找对应深度图深度值，并根据深度值计算对应的三维坐标，即可得到已匹配的三维坐标点对。根据已匹配三维坐标点对，计算两组三维数据集之间的旋转和平移矩阵。完成不同视角下三维点云之间的粗配准。3.3)三维点云的精配准是在已知相邻视角点云之间的初始旋转矩阵和平移矩阵前提下，采用ICP迭代最邻近点算法对相邻视角进行精配准，逐渐逼近最佳的匹配结果，优化获得的最优旋转矩阵和平移矩阵，所述最优即为函数值最小。3.4)如图10采集不同视角的深度图和RGB图，对深度图进行预处理，生成对应的三维点云。根据需要对三维点云数据进行降采样、去除离群点等预处理，然后相邻视角之间进行粗配准和精配准，得到两两视角之间的旋转和平移矩阵，可以根据需要转换到某一个视角的坐标系上，完成被重建物体的多视角的三维重建。上述实施例为本发明较佳的实施方式，但本发明的实施方式并不受所述实施例的限制，其他的任何未背离本发明的精神实质与原理下所作的改变、修饰、替代、组合、简化，均应为等效的置换方式，都包含在本发明的保护范围之内。当前第1页1 2 3