判别航天器身部激波/前缘类激波干扰发生条件及类型的方法与流程

本发明涉及一种判别航天器激波/激波干扰发生条件及类型的方法，尤其涉及一种通过高速航天器飞行状态和气动外形对身部激波和前缘类激波的干扰发生条件及类型进行快速判别的方法，属于航天器气动热环境分析领域。

背景技术：
：

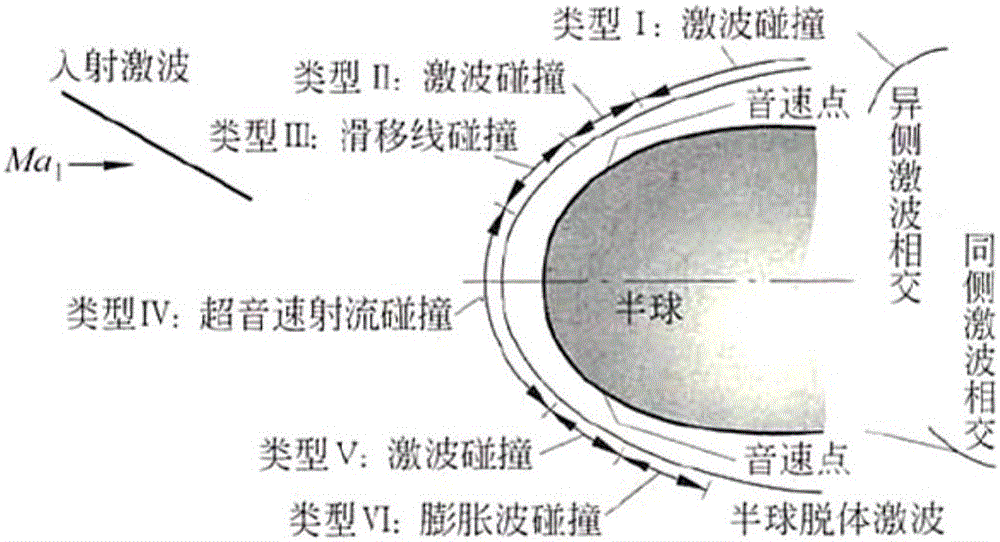
高速航天器通常具有水平翼、垂直安定面、控制舵等部件，头部激波向身部延伸，可能与上述各部件前缘脱体激波发生相交从而出现身部激波/前缘类激波干扰。而身部激波/前缘类激波干扰会对局部热流造成影响，严重时可能对飞行安全形成威胁。传统定义中，根据斜激波相对球头激波的入射位置将激波/激波干扰分为六种典型类型，如图2所示。而身部激波/前缘类激波干扰使得流场中产生了包括激波与剪切层在内的复杂波系结构，表现为多种不同的形式，传统的类型定义对于复杂的身部激波/前缘类激波干扰难以适用。

另外，现有的激波/激波干扰类型判别方法，需要通过数值模拟或地面试验获取激波干扰结构的详细信息方能对激波/激波干扰类型及作用位置进行判别，准确获取激波干扰结构详细信息又对数值模拟的网格数量、质量、模拟精度以及试验的流场结构捕捉能力提出非常高的要求；而激波干扰发生条件的判别则需要进行大量不同状态的数值模拟或地面试验方能获取。上述方法导致身部激波/前缘类激波干扰发生条件及类型判别周期长、难度大，难以在方案设计阶段为总体及气动外形设计提供防热约束条件。

技术实现要素：
：

本发明的技术解决问题是：克服现有技术的不足，提供判别航天器身部激波/前缘类激波干扰发生条件及类型的方法，适用于各种形式的身部激波/前缘类激波干扰，可大大缩减身部激波/前缘类激波干扰发生条件及类型的判别周期，降低判别难度，提高设计效率。

本发明的技术解决方案是：判别航天器身部激波/前缘类激波干扰发生条件及类型的方法，包括如下步骤：

(1)选择一道身部激波和一道前缘类激波作为待分析的两道激波，确定每道激波的参数；

(2)根据激波关系式建立激波干扰作用位置X与飞行状态和气动外形的定量关系；

(3)当激波干扰作用位置X位于产生两道激波的飞行器外形长度Ls范围内时，判定待分析的两道激波干扰发生条件成立，进入步骤(4)，否则，待分析的两道激波未发生干扰，判别结束；

(4)设来流依次经过身部激波和前缘类激波后流动的马赫数和压力分别为Ma₃、P₃，来流经过前缘类激波后流动的马赫数和压力分别为Ma₄、P₄，建立Ma₃、P₃、Ma₄、P₄与飞行状态和气动外形的定量关系，并根据飞行状态和气动外形参数求解Ma₃、P₃、Ma₄、P₄，当Ma₃>1&Ma₄>1&P₃>P₄时，判定身部激波/前缘类激波干扰类型为Ⅵ类激波/激波干扰；当Ma₃>1&Ma₄<1时，判定身部激波/前缘类激波干扰类型为V类激波/激波干扰；当Ma₃<1&Ma₄<1时，判定身部激波/前缘类激波干扰类型为IV类激波/激波干扰。

所述步骤(2)中，激波干扰作用位置X与飞行状态和气动外形的定量关系如下：

Ma₁为来流的初始马赫数，L为身部激波前部距前缘类激波前尖的距离，γ为来流气体比热比，θ为航天器身部楔角，λ为前缘后掠角，α为来流初始攻角。

所述步骤(4)中，Ma₃、P₃与飞行状态和气动外形的定量关系如下：

${{\mathrm{Ma}}_3}^2=\frac{{{\mathrm{Ma}}_2}^2+\frac{2}{\mathrm{\&gamma;}-1}}{\frac{2\mathrm{\&gamma;}}{\mathrm{\&gamma;}-1}{{\mathrm{Ma}}_2}^2{\sin }^2({\mathrm{\&beta;}}_2-\mathrm{\&theta;})-1}+\frac{{{\mathrm{Ma}}_2}^2{\cos }^2({\mathrm{\&beta;}}_2-\mathrm{\&theta;})}{\frac{\mathrm{\&gamma;}-1}{2}{{\mathrm{Ma}}_2}^2{\sin }^2({\mathrm{\&beta;}}_2-\mathrm{\&theta;})+1}$

$\frac{P_3}{P_2}=1+\frac{2\mathrm{\&gamma;}}{\mathrm{\&gamma;}+1}\&lsqb;{{\mathrm{Ma}}_2}^2{\sin }^2({\mathrm{\&beta;}}_2-\mathrm{\&theta;})-1\&rsqb;$

其中，

${{\mathrm{Ma}}_2}^2=\frac{{{\mathrm{Ma}}_1}^2+\frac{2}{\mathrm{\&gamma;}-1}}{\frac{2\mathrm{\&gamma;}}{\mathrm{\&gamma;}-1}{{\mathrm{Ma}}_1}^2{\sin }^2(\mathrm{\&alpha;}+{\mathrm{\&beta;}}_1)-1}+\frac{{{\mathrm{Ma}}_1}^2{\cos }^2(\mathrm{\&alpha;}+{\mathrm{\&beta;}}_1)}{\frac{\mathrm{\&gamma;}-1}{2}{{\mathrm{Ma}}_1}^2{\sin }^2(\mathrm{\&alpha;}+{\mathrm{\&beta;}}_1)+1},$

$\frac{P_2}{P_1}=1+\frac{2\mathrm{\&gamma;}}{\mathrm{\&gamma;}+1}\&lsqb;{{\mathrm{Ma}}_1}^2{\sin }^2(\mathrm{\&alpha;}+{\mathrm{\&beta;}}_1)-1\&rsqb;;$

$sin(\mathrm{\&alpha;}+{\mathrm{\&beta;}}_1)=\frac{1}{{\mathrm{Ma}}_1}+\frac{\mathrm{\&gamma;}+1}{2}\frac{{\mathrm{Ma}}_1}{\sqrt{{{\mathrm{Ma}}_1}^2-1}}sin(\mathrm{\&alpha;}+\mathrm{\&theta;});$

Ma₂为来流经过航天器身部激波后流动的马赫数，P₂为来流经过航天器身部激波后流动的压力，β₁为身部激波与航天器轴线之间的夹角，β₂为前缘后掠角的余角；

Ma₄、P₄与飞行状态和气动外形的定量关系如下：

${{\mathrm{Ma}}_4}^2=\frac{{{\mathrm{Ma}}_1}^2+\frac{2}{\mathrm{\&gamma;}-1}}{\frac{2\mathrm{\&gamma;}}{\mathrm{\&gamma;}-1}{{\mathrm{Ma}}_1}^2{\sin }^2(\mathrm{\&alpha;}+{\mathrm{\&beta;}}_2)-1}+\frac{{{\mathrm{Ma}}_1}^2{\cos }^2(\mathrm{\&alpha;}+{\mathrm{\&beta;}}_2)}{\frac{\mathrm{\&gamma;}-1}{2}{{\mathrm{Ma}}_1}^2{\sin }^2(\mathrm{\&alpha;}+{\mathrm{\&beta;}}_2)+1}$

$\frac{P_4}{P_1}=1+\frac{2\mathrm{\&gamma;}}{\mathrm{\&gamma;}+1}.\&lsqb;{{\mathrm{Ma}}_1}^2{\sin }^2(\mathrm{\&alpha;}+{\mathrm{\&beta;}}_2)-1\&rsqb;.$

与现有技术相比，本发明具有如下有益效果：

(1)本发明将根据斜激波相对球头激波的入射位置对激波/激波干扰类型进行划分的判别方式更新为以激波/激波干扰波系结构和流动特征为依据的判别方式，抓住了激波/激波干扰的物理本质，适用于各种形式的身部激波/前缘类激波干扰。事实上，本发明还可以进一步推广到所有激波/激波干扰，具有广泛的适用性。

(2)本发明提出的判别方法不再需要获取激波干扰结构详细信息，避免了大量不同状态的数值模拟或地面试验，从而大大缩减了判别周期，降低了判别难度，提高了设计效率。

附图说明：

图1为本发明流程图；

图2为传统激波干扰类型示意图；

图3为本发明实施例中高速航天器身部激波/前缘激波干扰示意图；

图4为本发明实施例中待分析的两道干扰激波参数示意图。

具体实施方式：

如图1所示，本发明提出一种判别高速航天器身部激波/前缘类激波干扰发生条件及类型的方法，包括如下步骤：

(1)选择一道身部激波和一道前缘类激波作为待分析的两道激波，确定每道激波的参数；

(2)根据激波关系式建立激波干扰作用位置X与飞行状态和气动外形的定量关系；

(3)当激波干扰作用位置X位于产生两道激波的飞行器外形长度Ls范围内时，判定待分析的两道激波干扰发生条件成立，进入步骤(4)，否则，待分析的两道激波未发生干扰，判别结束；

(4)建立身部激波/前缘类激波干扰类型判别特征参数与飞行状态和气动外形参数的关联关系，根据不同类型身部激波/前缘类激波干扰流动结构特征，对干扰类型作出快速判别。

步骤(4)的实现方法为：设来流依次经过身部激波和前缘类激波后流动的马赫数和压力分别为Ma₃、P₃，来流经过前缘类激波后流动的马赫数和压力分别为Ma₄、P₄，建立Ma₃、P₃、Ma₄、P₄与飞行状态和气动外形的定量关系，并根据飞行状态和气动外形参数求解Ma₃、P₃、Ma₄、P₄，当Ma₃>1&Ma₄>1&P₃>P₄时，判定身部激波/前缘类激波干扰类型为Ⅵ类激波/激波干扰；当Ma₃>1&Ma₄<1时，判定身部激波/前缘类激波干扰类型为V类激波/激波干扰；当Ma₃<1&Ma₄<1时，判定身部激波/前缘类激波干扰类型为IV类激波/激波干扰。

实施例：

以图3所示某高速航天器身部激波/迎风方向舵前缘激波干扰为例，本发明提出的快速判别身部激波/前缘类激波干扰发生条件及类型的方法具体实施步骤如下：

1.选择迎风方向舵前缘激波和身部激波作为待分析激波，如图4所示，身部激波及迎风方向舵前缘激波均可近似视作斜激波，圆圈内区域即为身部激波/前缘激波干扰区域。前缘激波附近流动主要由身部激波层外曝露于自由来流中的前缘激波后流动与身部激波层内依次经过身部激波和前缘激波后的流动组成。身部激波层内流动：自由来流(马赫数Ma₁、压力P₁)以攻角α流向航天器，经过航天器身部斜激波后流动方向发生偏折，形成与身部平行的流动(马赫数Ma₂、压力P₂)，到达前缘附近后，经过前缘激波后流动方向再次发生偏折，形成与前缘平行的流动(马赫数Ma₃、压力P₃)；身部激波层外流动：自由来流(马赫数Ma₁、压力P₁)以攻角α流向前缘，经过前缘激波后流动方向发生偏折，形成与前缘平行的流动(马赫数Ma₄、压力P₄)，图中θ为航天器身部楔角，β₁为身部激波与航天器轴线之间的夹角，λ为前缘后掠角，β₂为后掠角的余角。

2.根据激波关系式建立身部激波/前缘类激波干扰发生条件与飞行状态和气动外形的定量关系；图中L为身部激波前部距迎风方向舵前缘激波前尖的距离，L_s为模型总长(产生两道激波的飞行器外形长度)，X为身部激波/迎风方向舵前缘激波干扰轴向位置。根据方向舵前缘激波与身部激波几何关系，身部激波/迎风方向舵前缘激波干扰轴向位置表达式如下：

$X=\frac{{\mathrm{tan\&beta;}}_2\&CenterDot;L}{{\mathrm{tan\&beta;}}_2-tan({\mathrm{\&beta;}}_1+\mathrm{\&alpha;})}$

而由斜激波关系式：

$sin({\mathrm{\&beta;}}_1+\mathrm{\&alpha;})=\frac{1}{{\mathrm{Ma}}_1}+\frac{\mathrm{\&gamma;}+1}{2}\frac{{\mathrm{Ma}}_1}{\sqrt{{{\mathrm{Ma}}_1}^2-1}}sin(\mathrm{\&theta;}+\mathrm{\&alpha;})$

将上式代入身部激波/迎风方向舵前缘激波干扰轴向位置表达式，激波干扰作用位置可以表示为：

由图中几何关系可知，激波/激波发生干扰条件为：X≤Ls，即：

若上式成立，则迎风方向舵前缘激波和身部激波发生干扰，由身部激波/迎风方向舵前缘激波干扰轴向位置表达式即可求解得到身部激波/迎风方向舵前缘激波干扰轴向位置量值。否则不发生干扰。

3.身部激波/前缘激波干扰流动结构由来流依次经过身部激波和前缘激波后的马赫数和压力Ma₃、P₃，来流经过前缘激波后的马赫数和压力Ma₄、P₄之间的匹配关系决定。根据身部斜激波关系:

$sin(\mathrm{\&alpha;}+{\mathrm{\&beta;}}_1)=\frac{1}{{\mathrm{Ma}}_1}+\frac{\mathrm{\&gamma;}+1}{2}\frac{{\mathrm{Ma}}_1}{\sqrt{{{\mathrm{Ma}}_1}^2-1}}sin(\mathrm{\&alpha;}+\mathrm{\&theta;})$

${{\mathrm{Ma}}_2}^2=\frac{{{\mathrm{Ma}}_1}^2+\frac{2}{\mathrm{\&gamma;}-1}}{\frac{2\mathrm{\&gamma;}}{\mathrm{\&gamma;}-1}{{\mathrm{Ma}}_1}^2{\sin }^2(\mathrm{\&alpha;}+{\mathrm{\&beta;}}_1)-1}+\frac{{{\mathrm{Ma}}_1}^2{\cos }^2(\mathrm{\&alpha;}+{\mathrm{\&beta;}}_1)}{\frac{\mathrm{\&gamma;}-1}{2}{{\mathrm{Ma}}_1}^2{\sin }^2(\mathrm{\&alpha;}+{\mathrm{\&beta;}}_1)+1}$

$\frac{P_2}{P_1}=1+\frac{2\mathrm{\&gamma;}}{\mathrm{\&gamma;}+1}\&lsqb;{{\mathrm{Ma}}_1}^2{\sin }^2(\mathrm{\&alpha;}+{\mathrm{\&beta;}}_1)-1\&rsqb;$

同理，来流经过身部激波后再经过前缘激波，根据前缘斜激波关系：

${{\mathrm{Ma}}_3}^2=\frac{{{\mathrm{Ma}}_2}^2+\frac{2}{\mathrm{\&gamma;}-1}}{\frac{2\mathrm{\&gamma;}}{\mathrm{\&gamma;}-1}{{\mathrm{Ma}}_2}^2{\sin }^2({\mathrm{\&beta;}}_2-\mathrm{\&theta;})-1}+\frac{{{\mathrm{Ma}}_2}^2{\cos }^2({\mathrm{\&beta;}}_2-\mathrm{\&theta;})}{\frac{\mathrm{\&gamma;}-1}{2}{{\mathrm{Ma}}_2}^2{\sin }^2({\mathrm{\&beta;}}_2-\mathrm{\&theta;})+1}$

$\frac{P_3}{P_2}=1+\frac{2\mathrm{\&gamma;}}{\mathrm{\&gamma;}+1}\&lsqb;{{\mathrm{Ma}}_2}^2{\sin }^2({\mathrm{\&beta;}}_2-\mathrm{\&theta;})-1\&rsqb;$

来流经过前缘激波后，根据前缘斜激波关系：

${{\mathrm{Ma}}_4}^2=\frac{{{\mathrm{Ma}}_1}^2+\frac{2}{\mathrm{\&gamma;}-1}}{\frac{2\mathrm{\&gamma;}}{\mathrm{\&gamma;}-1}{{\mathrm{Ma}}_1}^2{\sin }^2(\mathrm{\&alpha;}+{\mathrm{\&beta;}}_2)-1}+\frac{{{\mathrm{Ma}}_1}^2{\cos }^2(\mathrm{\&alpha;}+{\mathrm{\&beta;}}_2)}{\frac{\mathrm{\&gamma;}-1}{2}{{\mathrm{Ma}}_1}^2{\sin }^2(\mathrm{\&alpha;}+{\mathrm{\&beta;}}_2)+1}$

$\frac{P_4}{P_1}=1+\frac{2\mathrm{\&gamma;}}{\mathrm{\&gamma;}+1}\&lsqb;{{\mathrm{Ma}}_1}^2{\sin }^2(\mathrm{\&alpha;}+{\mathrm{\&beta;}}_2)-1\&rsqb;.$

4.根据不同类型身部激波/前缘类激波干扰流动结构特征，对身部激波/前缘类激波干扰类型作出判别；将飞行状态和气动外形参数具体数值代入上一步中建立的关联关系中，即可求解得到身部激波/前缘类激波干扰类型判别特征参数(Ma₃、P₃、Ma₄、P₄)具体量值，结合不同类型身部激波/前缘类激波干扰流动结构特征即可对身部激波/前缘类激波干扰类型作出判别。在本实施例中，Ma₃>1&Ma₄>1&P₃>P₄，身部激波层内外的前缘激波均为弱激波，且经过两道斜激波之后气流的压力高于直接曝露于来流中的斜激波后压力，两道弱激波在相交点处形成膨胀波，形成Ⅵ类激波/激波干扰。

该高速航天器身部激波/前缘类激波干扰，如果采用传统干扰流场数值模拟对身部激波/前缘类激波干扰类型及发生条件进行判别，其耗费时间：按平均生成一套网格需要10天、完成一个状态计算需要4天来算，所需计算时间＝10+4*20＝90天；地面试验判别激波干扰发生条件及类型的时间：按平均加工一套试验模型需要15天、完成一个状态试验与测量需要2天来算，所需计算时间＝30+2*20＝70天；而本发明提出的判别方法：身部激波/前缘类激波干扰发生条件及类型判别仅需1小时左右。由此可见，本发明方法大大缩减了身部激波/前缘类激波干扰发生条件及类型的判别周期，降低了判别难度，提高了设计效率。

本发明提供的技术方案可用于其它各类激波/激波干扰。上述实施例只是对本发明的解释，而不能作为对本发明的限制，因此凡是与本发明思路类似的实施方式均在本发明的保护范围内。

本发明未详细说明部分属于本领域技术人员公知常识。