基于储能调度模式的分布式光伏两阶段多目标就地消纳法的制作方法

本发明涉及一种电力系统的经济运行、调度仿真方法。特别是涉及一种基于储能调度模式的分布式光伏两阶段多目标就地消纳法。
背景技术：
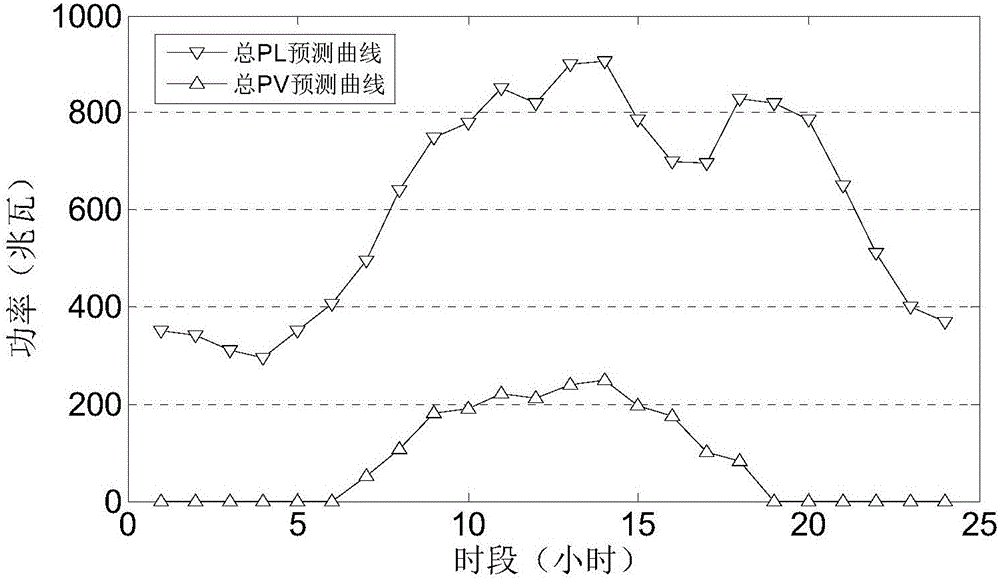
：2015年3月，《国家能源局关于下达2015年光伏发电建设实施方案的通知》出台，要求全年新增光伏电站建设规模达17.8GW，并优先建设35kV以下、20MW以下的接入配电网的分布式光伏电站项目。根据中国风能资源分布特点，未来中国风电发展将呈现大规模、高集中的开发趋势。而随着分布式光伏发电接入容量的提高，研究配电网光伏消纳能力及提高光伏消纳能力的措施具有重要的现实意义从系统的角度看，不同的电力系统对分布式光伏输出的接纳能力并不相同，尤其是快速响应能力低的系统，其消纳能力也较为有限。面对这样的情况，如果系统有充足的储能设备，则光伏的输出相对容易充分消纳，可更容易实现对光伏输出的平稳消纳而且能够满足系统的安全稳定需求，从而提高光伏的消纳能力。然而，当分布式光伏渗透率较低的情况下，传统的仅以光伏消纳率最高为目标的消纳模型得出的最优解通常不是唯一的，而且无法计及含分布式光伏配电网的运行效益。因此需要重新建立模型并在模型中计及其他目标，使得模型更加合理和符合实际。技术实现要素：本发明所要解决的技术问题是，提供一种可以在优化光伏消纳率的同时，更好地兼顾系统运行成本最小化目标的基于储能调度模式的分布式光伏两阶段多目标就地消纳法。本发明所采用的技术方案是：一种基于储能调度模式的分布式光伏两阶段多目标就地消纳法，包括如下步骤：1)采集含分布式光伏、储能以及火电机组的区域性电网历史运行数据，综合相应地区气象数据，对当地未来一天光伏出力及负荷进行预测，得到光伏出力预测曲线；2)将未来一天分为24个调度时段，以光伏集群的功率消纳率最高建立优先目标函数；3)建立次要目标函数，所述次要目标函数为多目标函数，包括以系统运行成本最小为目标的第一个子目标，以储能电量越限惩罚量最小为为目标的第二个子目标，其中，所述系统运行成本包括发电成本和网损成本；4)建立就地消纳模型所要满足的储能相关的约束条件，所述约束条件包括储能充放电上下限约束，储能电量与储能充放电功率关系的约束，以及储能首末电量约束，建立就地消纳模型所要满足的火电机组相关的约束条件，储能相关的约束条件、火电机组相关约束条件以及其他必要约束共同构成就地消纳模型的约束条件；所述其他必要约束包括节点电压约束、以及联络线传输功率约束；5)将优先目标函数和约束条件共同构成第一光伏集群就地消纳模型，对所所述第一光伏集群就地消纳模型进行求解得到：储能一天的出力计划曲线，机组一天的出力计划曲线，以及联络线一天的传输功率曲线；6)判断步骤5)求解结果是否唯一，如果唯一，则步骤5)的结果就是光伏集群就地消纳方案，如果步骤5)求解结果不唯一，则建立由次要目标函数和约束条件构成的第二光伏集群就地消纳模型，并以步骤5)中所有光伏集群就地消纳方案为寻优范围，对所述的第二光伏集群就地消纳模型求解得到光伏集群就地消纳方案。本发明的基于储能调度模式的分布式光伏两阶段多目标就地消纳法，具有如下优点：1、本发明的方法可以在优化光伏消纳率的同时，更好地兼顾系统运行成本最小化的目标。2、当分布式光伏渗透率较低的情况下，采用储能调度模式对分布式光伏消纳率的提升没有显著作用，当满足优先目标最优时的最优解不唯一，此时模型可以自主地计及次要目标即系统运行成本最低，制定经济的调度策略。3、当分布式光伏渗透率较高的情况下，模型自主地以优先目标即消纳率最大为目标，采用储能调度模式对分布式光伏消纳率的提升有显著作用。附图说明图1是本发明基于储能调度模式的分布式光伏两阶段多目标就地消纳法的流程图；图2是实例1低渗透率时负荷与光伏预测；图3是实例1消纳光伏策略；图4是实例2低渗透率时负荷与光伏预测；图5是实例2消纳光伏策略；图6是实例1和实例2一天各时段储能电量情况。具体实施方式下面结合实施例和附图对本发明的基于储能调度模式的分布式光伏两阶段多目标就地消纳法做出详细说明。如图1所示，本发明的基于储能调度模式的分布式光伏两阶段多目标就地消纳法，适用于含光伏电池、火电机组的区域电网，包括如下步骤：1)采集含分布式光伏、储能以及火电机组的区域性电网历史运行数据，综合相应地区气象数据，对当地未来一天光伏出力及负荷进行预测，得到光伏出力预测曲线；2)将未来一天分为24个调度时段，以光伏集群的功率消纳率最高建立优先目标函数，即最大化光伏消纳率，所述的优先目标函数为：F1=Σt=1TPPV(t)Σt=1TPPV,0(t)]]>式中：PPV，0(t)为光伏出力预测曲线中t时段功率；PPV(t)为t时段光伏实际消纳功率；3)建立次要目标函数，即最小化系统运行成本，所述次要目标函数为多目标函数，包括以系统运行成本最小为目标的第一个子目标，以储能电量越限惩罚量最小为为目标的第二个子目标，其中，所述系统运行成本包括发电成本和网损成本，所述的多目标模型包括：(1)发电成本数学模型：C1=Σt=1T(Σg=1Gfg(Pg(t)))ΔT]]>式中：C1为经济成本；G为总机组数；fg()为机组g所对应的成本曲线，以及包含了燃料成本、运行维护成本、设备折旧成本等必要成本；Pg(t)为机组g在t时段的出力；ΔT为每个时段对应的时长，本实施例中取为一小时；(2)网损成本数学模型如下：C2=Σt=1T(Σl=1LPloss,l(t))p(t)ΔT]]>式中：C2为网损成本；Ploss,l(t)为t时段线路l的网损，总线路数量为L；p(t)为t时段外网分时电价水平；(3)发电成本数学模型和网损成本数学模型共同构成次要目标中的第一个子目标，即：f1＝C1+C2(4)次要目标中的第二个子目标为储能电量越限惩罚项：f2＝λΔSSB(t)ΔSSB(t)=SSBmin-SSB(t)SSBmin,0≤SSB≤SSBmin0,SSBmin≤SSB≤SSBmaxSSB(t)-SSBmax1-SSBmax,SSBmax≤SSB(t)≤1]]>式中：λ储能电量越限惩罚系数；SSB(t)为t时段储能电量；为储能放电深度，为储能充电深度，可以选取为一般文献里对储能电量上下限进行约束的储能电量下限和上限；所建立的次要目标函数为：F2＝γ1f1+γ2f2,γ1+γ2＝1式中：γ1与γ2为权系数；4)在得出优先目标函数与次要目标函数之后，应当满足一定约束条件，因此，建立就地消纳模型所要满足的储能相关的约束条件，所述约束条件包括储能充放电上下限约束，储能电量与储能充放电功率关系的约束，以及储能首末电量约束，建立就地消纳模型所要满足的火电机组相关的约束条件，储能相关的约束条件、火电机组相关约束条件以及其他必要约束共同构成就地消纳模型的约束条件；所述其他必要约束包括节点电压约束、以及联络线传输功率约束，其中所述的储能充放电上下限约束为：PSBmin≤PSB(t)≤PSBmax]]>其中，表示储能放电功率上限，表示蓄电池功率下限；当为负时，相反数表示储能充电功率上限；所述的储能电量与储能充放电功率关系的约束为：SSB(t)＝SSB(t-1)-ΔTPSB(t)ηinSSB(t)＝SSB(t-1)-ΔTPSB(t)/ηout式中：SSB(t)为t时段蓄电池的荷电量；PSB(t)为t时段蓄电池功率，以放电为正方向；ηin为充电效率，ηout为放电效率；所述的储能首末电量约束为：SSB(0)＝SSB(T)式中：SSB(0)表示第一时段前的储能电量，SSB(T)表示一天最后一个时段末的储能电量。所述火电机组相关约束条件为机组出力上下限约束：Pgmin≤Pg(t)≤Pgmax]]>式中：为机组g的出力下限，为机组g的出力上限，该约束对任意时段t都成立。所述节点电压约束和联络线传输功率约束：Ufmin≤Uft≤Ufmax]]>式中：为t时段节点f的运行电压；和分别为节点f的运行电压最小值和运行电压最大值。Plmin≤Plt≤Plmax式中：Plt为t时段含分布式光伏接入配电网的线路l的运行传输功率；规定线路传输功率向某一个方向为正，则Plmax为正向传输功率上限，Plmin为负，其相反数为反向传输功率上限。5)将优先目标函数和约束条件共同构成第一光伏集群就地消纳模型，对所述第一光伏集群就地消纳模型进行求解得到：储能一天的出力计划曲线，机组一天的出力计划曲线，以及联络线一天的传输功率曲线；6)判断步骤5)求解结果是否唯一，如果唯一，则步骤5)的结果就是光伏集群就地消纳方案，如果步骤5)求解结果不唯一，则建立由次要目标函数和约束条件构成的第二光伏集群就地消纳模型，并以步骤5)中所有光伏集群就地消纳方案为寻优范围，对所述的第二光伏集群就地消纳模型求解得到光伏集群就地消纳方案。下面给出实例：本发明的基于储能调度模式的分布式光伏两阶段多目标就地消纳法，基于IEEE九节点系统构建了改进的含分布式光伏接入的系统。在实例中有3台发电机组分别为Gen1、Gen2、Gen3分别接入节点1、2、3，容量依次为400MW、400MW、200MW，其中节点1通过PCC与外网连接，可以由外网向该含分布式光伏的配电网传输功率，为了保证外网的安全可靠性，因此不考虑节点1通过PCC向外网售电的情况。在负荷节点5、6、8分别接入分布式光伏，接入容量相等，接入总容量在具体算例中根据要考察的渗透率而定；在节点9接入集中式储能系统蓄电池组，其配置容量为250MWh，充放电功率上限50MW。本发明主要研究分布式光伏有功功率的消纳模型，因此假定系统中无功功率充足而不考虑无功运行特性。实例1：光伏占比较低的情况。分布式光伏集群的总容量为250MW，渗透率为20％。备用容量取负荷的10％及光伏计划的20％，且不考虑机组检修和突发性误差等问题。系统中光伏预测曲线PV与负荷预测曲线PL如图2所示采用本发明的储能调度模式进行求解，可以得到结果该算例中可以做到光伏100％消纳，因此求解方法中的优化目标自动调整为综合经济性即次要目标。在不使用储能的情况下，全调度周期的综合成本为106858.7元，光伏就地消纳率100％；在加入储能的情况下，全调度周期的综合成本为103357.7元，光伏就地消纳率100％。这种情况下，模型的优先目标消纳率最高，容易得到满足且满足时的最优解不唯一，因此模型按照次要目标运行成本最小进行优化调度。在实例1中，储能主要作用是小额度的削峰填谷，由于火电机组的燃料成本曲线的斜率随着其出力的增大而增大，因此通过储能的削峰填谷作用可以让机组尽量运行在效率较高的低斜率部分，从而降低运行成本。事实上，算例一中综合成本降低了3.3％，各机组以及储能充放电状况如图3所示。实例2：同算例一，只按比例改变光伏的总装机容量，将其提高到875MW，此时渗透率为70％，这个数据意味着在光伏输出高峰时对其他发电单元有明显的替代效果。高渗透率下系统中光伏预测曲线PV与负荷预测曲线PL如图4所示。在不使用储能的情况下光伏消纳率为98.17％，综合成本65177.83元；使用储能的情况下，光伏消纳率提高到100％，综合成本为63831.52元。可以看出，储能的合理调度实现了光伏就地消纳率的提升，将本来难以消纳的部分也得以充分利用，光伏消纳率提高了1.83％，实现了就地充分消纳；综合成本降低了2.06％，相比之下效果没有光伏占比较低的情况更显著，这是因为当分布式光伏渗透率较高时，可以大大降低机组出力，使得机组更倾向于运行于燃料成本曲线的高效率部分，而使得通过储能进一步提高效率的空间相对有限，所以通过储能削峰填谷的成本下降效益没有算例一显著。在这种情况下，模型按照优先目标进行优化调度，当优先目标既光伏消纳率达到最大时，此时优化运行结果唯一；事实上，实例2中的各机组出力曲线以及储能充放电状况如图5所示。具体分析储能的作用可以看出，在光伏高峰阶段储能主要是吸收能量，而在晚上负荷小高峰但光伏无输出的情况下，储能放电，实现了光伏功率的更充分利用，整体满足合理利用的要求。在上述两个实例中，储能的一天各时段电量情况如图6所示。在实例1中，储能的作用主要是削峰填谷，因此其电量在负荷高峰时期较低；而在实例2中，储能调度的主要目的是提高光伏消纳率，因此在光伏大量并网时充分充电，其电量在光伏出力大时较高。当前第1页1 2 3