一种复杂场景下的目标车辆视频跟踪系统的制作方法

本发明涉及目标车辆跟踪技术领域，具体涉及一种复杂场景下的目标车辆视频跟踪系统。

背景技术：

随着计算机技术和图像处理技术的不断发展，基于视频技术的目标车辆检测与跟踪系统已成为智能交通系统的核心内容和关键技术。相关技术中的基于视频技术的检测与跟踪系统处理速度快、安装维护便捷且费用较低，并且监视范围广，可获取更多种类的交通参数，然而所述系统在采集包含目标车辆的视频时存在视频抖动的问题，进而影响后续的图像处理，系统处理视频图像的精度不高。

技术实现要素：

为解决上述问题，本发明旨在提供一种复杂场景下的目标车辆视频跟踪系统。

本发明的目的采用以下技术方案来实现：

一种复杂场景下的目标车辆视频跟踪系统，包括目标车辆视频采集装置、视频稳像装置、目标车辆追踪装置和目标车辆位置更新装置，所述目标车辆视频采集装置用于采集包含目标车辆的视频；所述视频稳像装置用于对采集的视频进行预处理，消除视频抖动的影响；所述目标车辆追踪装置用于对视频中的所述目标车辆进行检测和跟踪，最终获得所述目标车辆的检测跟踪结果；所述目标车辆位置更新装置用于利用所述检测跟踪结果通过在线学习更新所述目标车辆追踪装置，进而更新所述目标车辆的位置。

本发明的有益效果为：设置视频稳像装置对采集的视频图像进行预处理，消除视频抖动的影响，从而解决了上述的技术问题。

附图说明

利用附图对本发明作进一步说明，但附图中的应用场景不构成对本发明的任何限制，对于本领域的普通技术人员，在不付出创造性劳动的前提下，还可以根据以下附图获得其它的附图。

图1是本发明的结构示意图；

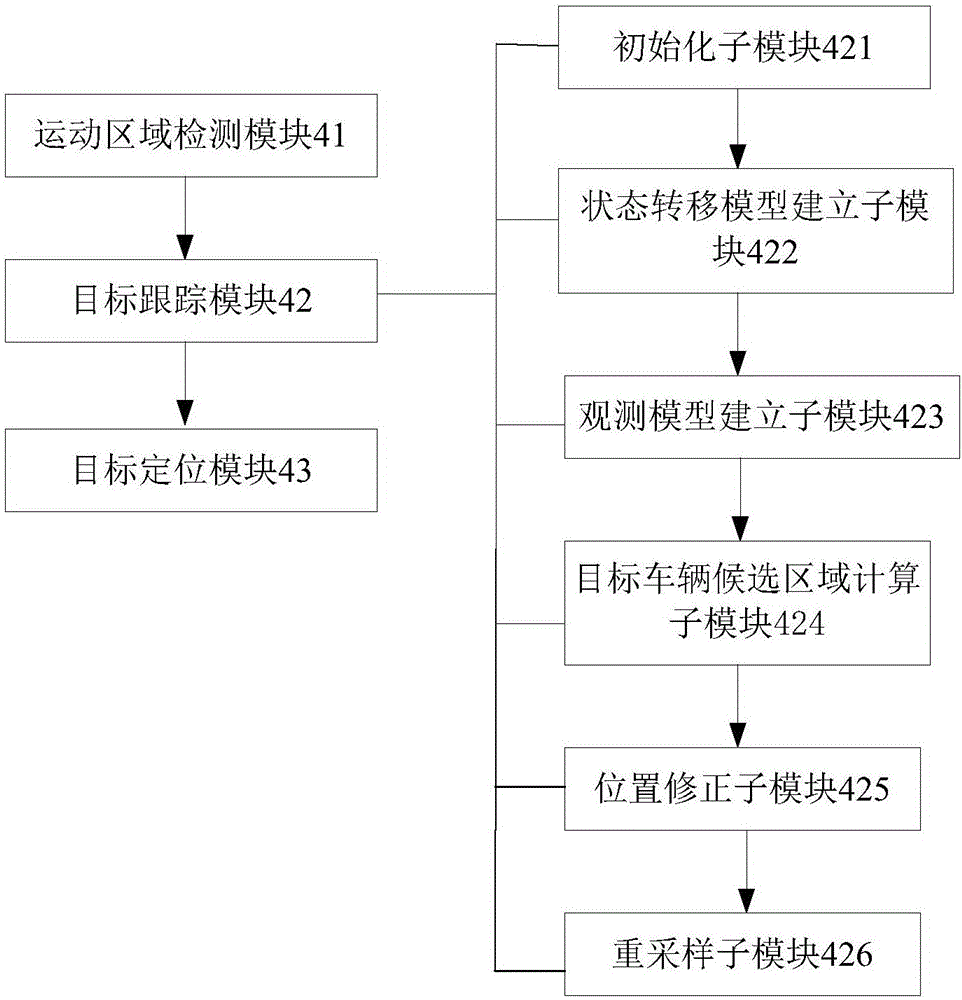
图2是本发明目标车辆追踪装置的模块连接示意图。

附图标记：

目标车辆视频采集装置1、视频稳像装置2、目标车辆追踪装置3、目标车辆位置更新装置4、高速相机11、视频图像采集器12、运动区域检测模块41、目标跟踪模块42、目标定位模块43、初始化子模块421、状态转移模型建立子模块422、观测模型建立子模块423、目标车辆候选区域计算子模块424、位置修正子模块425、重采样子模块426。

具体实施方式

结合以下应用场景对本发明作进一步描述。

应用场景1

参见图1、图2，本应用场景的一个实施例的复杂场景下的目标车辆视频跟踪系统，包括目标车辆视频采集装置1、视频稳像装置2、目标车辆追踪装置3、目标车辆位置更新装置4，所述目标车辆视频采集装置1用于采集包含目标车辆的视频；所述视频稳像装置2用于对采集的视频进行预处理，消除视频抖动的影响；所述目标车辆追踪装置3用于对视频中的所述目标车辆进行检测和跟踪，最终获得所述目标车辆的检测跟踪结果；所述目标车辆位置更新装置4用于利用所述检测跟踪结果通过在线学习更新所述目标车辆追踪装置3，进而更新所述目标车辆的位置。

优选的，所述目标车辆视频采集装置1包括高速相机11和与高速相机11连接的视频图像采集器12，所述视频图像采集器12用于采集目标车辆视频中的视频图像。

本发明上述实施例设置视频稳像装置2对采集的视频图像进行预处理，消除视频抖动的影响，从而解决了上述的技术问题。

优选的，所述对采集的视频进行预处理，包括：选定所述视频图像的第一帧图像为参考帧，并将参考帧平均划分为互不重叠的四个区域，W表示图像的宽度，H表示图像高度，四个区域大小均为0.5W×0.5H，从图像左上开始按照顺时针方向依次为区域1、2、3、4；在下一帧接收到的图像中心位置选定区域A₀，A₀的大小选定为0.5W×0.5H；将A₀按照上述方法划分为大小为0.25W×0.25H的四个图像子块A₁、A₂、A₃、A₄，A₁和A₂用于估算垂直方向上的局部运动向量，A₃和A₄用于估算水平方向上的局部运动向量，令A₁、A₂、A₃、A₄分别在1、2、3、4四个区域内搜寻最佳匹配，从而估计出视频序列的全局运动矢量，然后进行反向运动补偿，消除视频抖动的影响。

本优选实施例完善了视频稳像装置2对采集的视频图像进行预处理的功能，对视频图像进行稳像，避免了视频抖动对后续图像处理造成的影响，预处理的效率高。

优选的，所述目标车辆追踪装置3包括运动区域检测模块41、目标跟踪模块42和目标定位模块43；所述运动区域检测模块41用于在视频图像的一帧图像中检测目标车辆的运动区域D₁并以此作为目标模板；所述目标跟踪模块42用于建立粒子状态转移和观测模型并基于上述模型，采用粒子滤波预测目标车辆候选区域；所述目标定位模块43用于对所述目标车辆候选区域和所述目标模板进行特征相似度量，获得所述目标车辆的检测跟踪结果，即目标车辆的位置。

本优选实施例构建了目标车辆追踪装置3的模块架构。

优选的，所述目标跟踪模块42包括：

(1)初始化子模块421：用于在所述运动区域D₁内随机选取数量为n的粒子并对各粒子进行初始化处理，初始化处理后粒子的初始状态为x₀ⁱ，初始权值为{Q_oⁱ＝1/n,i＝1,...n}；

(2)状态转移模型建立子模块422：用于建立粒子状态转移模型，所述粒子状态转移模型采用下式：

$x_m^i={\mathrm{Ax}}_{m-1}^i+v_m^i$

式中，表示m时刻的新粒子，m≥2，为均值为0的高斯白噪声，A为4阶单位阵；m-1时刻的粒子通过状态转移模型传播；

(3)观测模型建立子模块423，用于通过颜色直方图、纹理特征直方图和运动边缘特征相结合的方式建立粒子观测模型；

(4)目标车辆候选区域计算子模块424：其利用最小方差估计来计算目标车辆候选区域：

$x_{now}=\underset{j=1}{\overset{n}{\Σ}}{Q}_m^j\·x_m^j$

式中，x_now表示计算的当前帧图像的目标车辆候选区域，表示m时刻第j个粒子的对应状态值；

(5)位置修正子模块425：用于修正异常数据：

$x_{pre}=\underset{j=1}{\overset{n}{\Σ}}{Q}_{m-1}^j\·x_{m-1}^j$

式中，x_pre表示计算的当前帧图像的目标车辆候选区域，表示m-1时刻第j个粒子的对应状态值；

设置数据异常评价函数P＝|x_now-x_pre|，若P的值大于设定的经验值T,则x_now＝x_pre；

(6)重采样子模块426：用于通过重采样操作删除权值过小的粒子，重采样时，利用系统当前时刻预测和观测的差值提供新息残差，进而通过量测新息残差对采样的粒子进行在线自适应性调整，采样过程中粒子数量和信息残差之间的关系定义为：

其中，N_m表示采样过程中m时刻的粒子数量，N_max和N_min分别表示最小和最大粒子数，N_min+1表示仅大于N_min的粒子数，N_max-1表示仅小于N_max的粒子数，表示m时刻系统的新息残差。

本优选实施例采用基于颜色直方图、纹理特征直方图和运动边缘特征相结合的方式进行采样粒子的权值更新，有效增强了跟踪系统的鲁棒性；设置位置修正子模块425，能够避免异常数据对整个系统带来的影响；在重采样子模块426中，利用当前时刻预测和观测的差值提供新息残差，进而通过量测新息残差对采样的粒子进行在线自适应性调整，并定义了采样过程中粒子数量和信息残差之间的关系，较好地保证了粒子采样的高效性和算法的实时性。

优选地，所述粒子观测模型的粒子权值更新公式为：

$Q_m^j=\frac{\stackrel{\‾}{Q_{Cm}^j}\·\stackrel{\‾}{Q_{Mm}^j}\·\stackrel{\‾}{Q_{Wm}^j}+{\mathrm{\λ}}_1\stackrel{\‾}{Q_{Cm}^j}+{{\mathrm{\λ}}_2}^2\stackrel{\‾}{Q_{Mm}^j}+{{\mathrm{\λ}}_2}^3\stackrel{\‾}{Q_{Wm}^j}+{\mathrm{\λ}}_1{\mathrm{\λ}}_2{\mathrm{\λ}}_3}{(1+{\mathrm{\λ}}_1)(1+{\mathrm{\λ}}_2)(1+{\mathrm{\λ}}_3)}$

式中

$\stackrel{\‾}{Q_{Cm}^j}=Q_{Cm}^j/\underset{j=1}{\overset{n}{\Σ}}{Q}_{Cm}^j,Q_{Cm}^j=Q_{C(m-1)}^j\frac{1}{\sqrt{2\mathrm{\π}\mathrm{\σ}}}\exp \left(-\frac{A_m^2}{2{\mathrm{\σ}}^2}\right)$

$\stackrel{\‾}{Q_{Mm}^j}=Q_{Mm}^j/\underset{j=1}{\overset{n}{\Σ}}{Q}_{Mm}^j,Q_{Mm}^j=Q_{M(m-1)}^j\frac{1}{\sqrt{2\mathrm{\π}\mathrm{\σ}}}\exp \left(-\frac{B_m^2}{2{\mathrm{\σ}}^2}\right)$

$\stackrel{\‾}{Q_{Wm}^j}=Q_{Wm}^j/\underset{j=1}{\overset{n}{\Σ}}{Q}_{Wm}^j,Q_{Wm}^j=Q_{W(m-1)}^j\frac{1}{\sqrt{2\mathrm{\π}\mathrm{\σ}}}\exp \left(-\frac{C_m^2}{2{\mathrm{\σ}}^2}\right)$

其中，表示m时刻第j个粒子的最终更新权值，和分别表示m时刻和m-1时刻中第j个粒子基于颜色直方图的更新权值，表示m时刻和m-1时刻中第j个粒子基于运动边缘的更新权值，表示m时刻和m-1时刻中第j个粒子基于纹理特征直方图的更新权值，A_m为m时刻中第j个粒子基于颜色直方图的观测值与真实值之间的Bhattacharrya距离，B_m为m时刻中第j个粒子基于运动边缘的观测值与真实值之间的Bhattacharrya距离,C_m为m时刻中第j个粒子基于纹理特征直方图的观测值与真实值之间的Bhattacharrya距离,σ为高斯似然模型方差，λ₁为基于颜色直方图的特征权值归一化的自适应调整因子，λ₂为基于运动边缘的特征权值归一化的自适应调整因子,λ₃为基于纹理特征直方图的特征权值归一化的自适应调整因子；

所述自适应调整因子的计算公式为：

${\mathrm{\λ}}_s^m={\mathrm{\ξ}}_{m-1}\·\[-\underset{j=1}{\overset{n}{\Σ}}\left(p_{m-1}^{s/j}\right){\log }_2^{p_{m-1}^{s/j}}\],s=1,2,3;$

其中，s＝1时，表示m时刻中基于颜色直方图的特征权值归一化的自适应调整因子，为m-1时刻中基于颜色直方图的特征值在j个粒子下的观测概率值；s＝2时，表示m时刻中基于运动边缘的特征权值归一化的自适应调整因子，为m-1时刻中基于运动边缘的特征值在j个粒子下的观测概率值；s＝3时，表示m时刻中基于纹理特征直方图的特征权值归一化的自适应调整因子，为m-1时刻中基于纹理特征直方图的特征值在j个粒子下的观测概率值；ξ_m-1表示在m-1时刻中所有粒子的空间位置方差值。

本优选实施例提出粒子观测模型的粒子权值更新公式和自适应调整因子的计算公式，对粒子的特征权值进行融合处理，有效克服了加性融合和乘性融合存在的缺陷，进一步增强了跟踪系统的鲁棒性。

在此应用场景中，选取粒子数n＝50，跟踪速度相对提高了8％，跟踪精度相对提高了7％。

应用场景2

参见图1、图2，本应用场景的一个实施例的复杂场景下的目标车辆视频跟踪系统，包括目标车辆视频采集装置1、视频稳像装置2、目标车辆追踪装置3、目标车辆位置更新装置4，所述目标车辆视频采集装置1用于采集包含目标车辆的视频；所述视频稳像装置2用于对采集的视频进行预处理，消除视频抖动的影响；所述目标车辆追踪装置3用于对视频中的所述目标车辆进行检测和跟踪，最终获得所述目标车辆的检测跟踪结果；所述目标车辆位置更新装置4用于利用所述检测跟踪结果通过在线学习更新所述目标车辆追踪装置3，进而更新所述目标车辆的位置。

优选的，所述目标车辆视频采集装置1包括高速相机11和与高速相机11连接的视频图像采集器12，所述视频图像采集器12用于采集目标车辆视频中的视频图像。

本发明上述实施例设置视频稳像装置2对采集的视频图像进行预处理，消除视频抖动的影响，从而解决了上述的技术问题。

优选的，所述对采集的视频进行预处理，包括：选定所述视频图像的第一帧图像为参考帧，并将参考帧平均划分为互不重叠的四个区域，W表示图像的宽度，H表示图像高度，四个区域大小均为0.5W×0.5H，从图像左上开始按照顺时针方向依次为区域1、2、3、4；在下一帧接收到的图像中心位置选定区域A₀，A₀的大小选定为0.5W×0.5H；将A₀按照上述方法划分为大小为0.25W×0.25H的四个图像子块A₁、A₂、A₃、A₄，A₁和A₂用于估算垂直方向上的局部运动向量，A₃和A₄用于估算水平方向上的局部运动向量，令A₁、A₂、A₃、A₄分别在1、2、3、4四个区域内搜寻最佳匹配，从而估计出视频序列的全局运动矢量，然后进行反向运动补偿，消除视频抖动的影响。

本优选实施例完善了视频稳像装置2对采集的视频图像进行预处理的功能，对视频图像进行稳像，避免了视频抖动对后续图像处理造成的影响，预处理的效率高。

优选的，所述目标车辆追踪装置3包括运动区域检测模块41、目标跟踪模块42和目标定位模块43；所述运动区域检测模块41用于在视频图像的一帧图像中检测目标车辆的运动区域D₁并以此作为目标模板；所述目标跟踪模块42用于建立粒子状态转移和观测模型并基于上述模型，采用粒子滤波预测目标车辆候选区域；所述目标定位模块43用于对所述目标车辆候选区域和所述目标模板进行特征相似度量，获得所述目标车辆的检测跟踪结果，即目标车辆的位置。

本优选实施例构建了目标车辆追踪装置3的模块架构。

优选的，所述目标跟踪模块42包括：

(1)初始化子模块421：用于在所述运动区域D₁内随机选取数量为n的粒子并对各粒子进行初始化处理，初始化处理后粒子的初始状态为x₀ⁱ，初始权值为{Q_oⁱ＝1/n,i＝1,...n}；

(2)状态转移模型建立子模块422：用于建立粒子状态转移模型，所述粒子状态转移模型采用下式：

$x_m^i={\mathrm{Ax}}_{m-1}^i+v_m^i$

式中，表示m时刻的新粒子，m≥2，为均值为0的高斯白噪声，A为4阶单位阵；m-1时刻的粒子通过状态转移模型传播；

(3)观测模型建立子模块423，用于通过颜色直方图、纹理特征直方图和运动边缘特征相结合的方式建立粒子观测模型；

(4)目标车辆候选区域计算子模块424：其利用最小方差估计来计算目标车辆候选区域：

$x_{now}=\underset{j=1}{\overset{n}{\Σ}}{Q}_m^j\·x_m^j$

式中，x_now表示计算的当前帧图像的目标车辆候选区域，表示m时刻第j个粒子的对应状态值；

(5)位置修正子模块425：用于修正异常数据：

$x_{pre}=\underset{j=1}{\overset{n}{\Σ}}{Q}_{m-1}^j\·x_{m-1}^j$

式中，x_pre表示计算的当前帧图像的目标车辆候选区域，表示m-1时刻第j个粒子的对应状态值；

设置数据异常评价函数P＝|x_now-x_pre|，若P的值大于设定的经验值T,则x_now＝x_pre；

(6)重采样子模块426：用于通过重采样操作删除权值过小的粒子，重采样时，利用系统当前时刻预测和观测的差值提供新息残差，进而通过量测新息残差对采样的粒子进行在线自适应性调整，采样过程中粒子数量和信息残差之间的关系定义为：

其中，N_m表示采样过程中m时刻的粒子数量，N_max和N_min分别表示最小和最大粒子数，N_min+1表示仅大于N_min的粒子数，N_max-1表示仅小于N_max的粒子数，表示m时刻系统的新息残差。

本优选实施例采用基于颜色直方图、纹理特征直方图和运动边缘特征相结合的方式进行采样粒子的权值更新，有效增强了跟踪系统的鲁棒性；设置位置修正子模块425，能够避免异常数据对整个系统带来的影响；在重采样子模块426中，利用当前时刻预测和观测的差值提供新息残差，进而通过量测新息残差对采样的粒子进行在线自适应性调整，并定义了采样过程中粒子数量和信息残差之间的关系，较好地保证了粒子采样的高效性和算法的实时性。

优选地，所述粒子观测模型的粒子权值更新公式为：

$Q_m^j=\frac{\stackrel{\‾}{Q_{Cm}^j}\·\stackrel{\‾}{Q_{Mm}^j}\·\stackrel{\‾}{Q_{Wm}^j}+{\mathrm{\λ}}_1\stackrel{\‾}{Q_{Cm}^j}+{{\mathrm{\λ}}_2}^2\stackrel{\‾}{Q_{Mm}^j}+{{\mathrm{\λ}}_2}^3\stackrel{\‾}{Q_{Wm}^j}+{\mathrm{\λ}}_1{\mathrm{\λ}}_2{\mathrm{\λ}}_3}{(1+{\mathrm{\λ}}_1)(1+{\mathrm{\λ}}_2)(1+{\mathrm{\λ}}_3)}$

式中

$\stackrel{\‾}{Q_{Cm}^j}=Q_{Cm}^j/\underset{j=1}{\overset{n}{\Σ}}{Q}_{Cm}^j,Q_{Cm}^j=Q_{C(m-1)}^j\frac{1}{\sqrt{2\mathrm{\π}\mathrm{\σ}}}\exp \left(-\frac{A_m^2}{2{\mathrm{\σ}}^2}\right)$

$\stackrel{\‾}{Q_{Mm}^j}=Q_{Mm}^j/\underset{j=1}{\overset{n}{\Σ}}{Q}_{Mm}^j,Q_{Mm}^j=Q_{M(m-1)}^j\frac{1}{\sqrt{2\mathrm{\π}\mathrm{\σ}}}\exp \left(-\frac{B_m^2}{2{\mathrm{\σ}}^2}\right)$

$\stackrel{\‾}{Q_{Wm}^j}=Q_{Wm}^j/\underset{j=1}{\overset{n}{\Σ}}{Q}_{Wm}^j,Q_{Wm}^j=Q_{W(m-1)}^j\frac{1}{\sqrt{2\mathrm{\π}\mathrm{\σ}}}\exp \left(-\frac{C_m^2}{2{\mathrm{\σ}}^2}\right)$

其中，表示m时刻第j个粒子的最终更新权值，和分别表示m时刻和m-1时刻中第j个粒子基于颜色直方图的更新权值，表示m时刻和m-1时刻中第j个粒子基于运动边缘的更新权值，表示m时刻和m-1时刻中第j个粒子基于纹理特征直方图的更新权值，A_m为m时刻中第j个粒子基于颜色直方图的观测值与真实值之间的Bhattacharrya距离，B_m为m时刻中第j个粒子基于运动边缘的观测值与真实值之间的Bhattacharrya距离,C_m为m时刻中第j个粒子基于纹理特征直方图的观测值与真实值之间的Bhattacharrya距离,σ为高斯似然模型方差，λ₁为基于颜色直方图的特征权值归一化的自适应调整因子，λ₂为基于运动边缘的特征权值归一化的自适应调整因子,λ₃为基于纹理特征直方图的特征权值归一化的自适应调整因子；

所述自适应调整因子的计算公式为：

${\mathrm{\λ}}_s^m={\mathrm{\ξ}}_{m-1}\·\[-\underset{j=1}{\overset{n}{\Σ}}\left(p_{m-1}^{s/j}\right){\log }_2^{p_{m-1}^{s/j}}\],s=1,2,3;$

其中，s＝1时，表示m时刻中基于颜色直方图的特征权值归一化的自适应调整因子，为m-1时刻中基于颜色直方图的特征值在j个粒子下的观测概率值；s＝2时，表示m时刻中基于运动边缘的特征权值归一化的自适应调整因子，为m-1时刻中基于运动边缘的特征值在j个粒子下的观测概率值；s＝3时，表示m时刻中基于纹理特征直方图的特征权值归一化的自适应调整因子，为m-1时刻中基于纹理特征直方图的特征值在j个粒子下的观测概率值；ξ_m-1表示在m-1时刻中所有粒子的空间位置方差值。

本优选实施例提出粒子观测模型的粒子权值更新公式和自适应调整因子的计算公式，对粒子的特征权值进行融合处理，有效克服了加性融合和乘性融合存在的缺陷，进一步增强了跟踪系统的鲁棒性。

在此应用场景中，选取粒子数n＝55，跟踪速度相对提高了7％，跟踪精度相对提高了8％。

应用场景3

参见图1、图2，本应用场景的一个实施例的复杂场景下的目标车辆视频跟踪系统，包括目标车辆视频采集装置1、视频稳像装置2、目标车辆追踪装置3、目标车辆位置更新装置4，所述目标车辆视频采集装置1用于采集包含目标车辆的视频；所述视频稳像装置2用于对采集的视频进行预处理，消除视频抖动的影响；所述目标车辆追踪装置3用于对视频中的所述目标车辆进行检测和跟踪，最终获得所述目标车辆的检测跟踪结果；所述目标车辆位置更新装置4用于利用所述检测跟踪结果通过在线学习更新所述目标车辆追踪装置3，进而更新所述目标车辆的位置。

优选的，所述目标车辆视频采集装置1包括高速相机11和与高速相机11连接的视频图像采集器12，所述视频图像采集器12用于采集目标车辆视频中的视频图像。

本发明上述实施例设置视频稳像装置2对采集的视频图像进行预处理，消除视频抖动的影响，从而解决了上述的技术问题。

优选的，所述对采集的视频进行预处理，包括：选定所述视频图像的第一帧图像为参考帧，并将参考帧平均划分为互不重叠的四个区域，W表示图像的宽度，H表示图像高度，四个区域大小均为0.5W×0.5H，从图像左上开始按照顺时针方向依次为区域1、2、3、4；在下一帧接收到的图像中心位置选定区域A₀，A₀的大小选定为0.5W×0.5H；将A₀按照上述方法划分为大小为0.25W×0.25H的四个图像子块A₁、A₂、A₃、A₄，A₁和A₂用于估算垂直方向上的局部运动向量，A₃和A₄用于估算水平方向上的局部运动向量，令A₁、A₂、A₃、A₄分别在1、2、3、4四个区域内搜寻最佳匹配，从而估计出视频序列的全局运动矢量，然后进行反向运动补偿，消除视频抖动的影响。

本优选实施例完善了视频稳像装置2对采集的视频图像进行预处理的功能，对视频图像进行稳像，避免了视频抖动对后续图像处理造成的影响，预处理的效率高。

优选的，所述目标车辆追踪装置3包括运动区域检测模块41、目标跟踪模块42和目标定位模块43；所述运动区域检测模块41用于在视频图像的一帧图像中检测目标车辆的运动区域D₁并以此作为目标模板；所述目标跟踪模块42用于建立粒子状态转移和观测模型并基于上述模型，采用粒子滤波预测目标车辆候选区域；所述目标定位模块43用于对所述目标车辆候选区域和所述目标模板进行特征相似度量，获得所述目标车辆的检测跟踪结果，即目标车辆的位置。

本优选实施例构建了目标车辆追踪装置3的模块架构。

优选的，所述目标跟踪模块42包括：

(1)初始化子模块421：用于在所述运动区域D₁内随机选取数量为n的粒子并对各粒子进行初始化处理，初始化处理后粒子的初始状态为x₀ⁱ，初始权值为{Q_oⁱ＝1/n,i＝1,...n}；

(2)状态转移模型建立子模块422：用于建立粒子状态转移模型，所述粒子状态转移模型采用下式：

$x_m^i={\mathrm{Ax}}_{m-1}^i+v_m^i$

式中，表示m时刻的新粒子，m≥2，为均值为0的高斯白噪声，A为4阶单位阵；m-1时刻的粒子通过状态转移模型传播；

(3)观测模型建立子模块423，用于通过颜色直方图、纹理特征直方图和运动边缘特征相结合的方式建立粒子观测模型；

(4)目标车辆候选区域计算子模块424：其利用最小方差估计来计算目标车辆候选区域：

$x_{now}=\underset{j=1}{\overset{n}{\Σ}}{Q}_m^j\·x_m^j$

式中，x_now表示计算的当前帧图像的目标车辆候选区域，表示m时刻第j个粒子的对应状态值；

(5)位置修正子模块425：用于修正异常数据：

$x_{pre}=\underset{j=1}{\overset{n}{\Σ}}{Q}_{m-1}^j\·x_{m-1}^j$

式中，x_pre表示计算的当前帧图像的目标车辆候选区域，表示m-1时刻第j个粒子的对应状态值；

设置数据异常评价函数P＝|x_now-x_pre|，若P的值大于设定的经验值T,则x_now＝x_pre；

(6)重采样子模块426：用于通过重采样操作删除权值过小的粒子，重采样时，利用系统当前时刻预测和观测的差值提供新息残差，进而通过量测新息残差对采样的粒子进行在线自适应性调整，采样过程中粒子数量和信息残差之间的关系定义为：

其中，N_m表示采样过程中m时刻的粒子数量，N_max和N_min分别表示最小和最大粒子数，N_min+1表示仅大于N_min的粒子数，N_max-1表示仅小于N_max的粒子数，表示m时刻系统的新息残差。

本优选实施例采用基于颜色直方图、纹理特征直方图和运动边缘特征相结合的方式进行采样粒子的权值更新，有效增强了跟踪系统的鲁棒性；设置位置修正子模块425，能够避免异常数据对整个系统带来的影响；在重采样子模块426中，利用当前时刻预测和观测的差值提供新息残差，进而通过量测新息残差对采样的粒子进行在线自适应性调整，并定义了采样过程中粒子数量和信息残差之间的关系，较好地保证了粒子采样的高效性和算法的实时性。

优选地，所述粒子观测模型的粒子权值更新公式为：

$Q_m^j=\frac{\stackrel{\‾}{Q_{Cm}^j}\·\stackrel{\‾}{Q_{Mm}^j}\·\stackrel{\‾}{Q_{Wm}^j}+{\mathrm{\λ}}_1\stackrel{\‾}{Q_{Cm}^j}+{{\mathrm{\λ}}_2}^2\stackrel{\‾}{Q_{Mm}^j}+{{\mathrm{\λ}}_2}^3\stackrel{\‾}{Q_{Wm}^j}+{\mathrm{\λ}}_1{\mathrm{\λ}}_2{\mathrm{\λ}}_3}{(1+{\mathrm{\λ}}_1)(1+{\mathrm{\λ}}_2)(1+{\mathrm{\λ}}_3)}$

式中

$\stackrel{\‾}{Q_{Cm}^j}=Q_{Cm}^j/\underset{j=1}{\overset{n}{\Σ}}{Q}_{Cm}^j,Q_{Cm}^j=Q_{C(m-1)}^j\frac{1}{\sqrt{2\mathrm{\π}\mathrm{\σ}}}\exp \left(-\frac{A_m^2}{2{\mathrm{\σ}}^2}\right)$

$\stackrel{\‾}{Q_{Mm}^j}=Q_{Mm}^j/\underset{j=1}{\overset{n}{\Σ}}{Q}_{Mm}^j,Q_{Mm}^j=Q_{M(m-1)}^j\frac{1}{\sqrt{2\mathrm{\π}\mathrm{\σ}}}\exp \left(-\frac{B_m^2}{2{\mathrm{\σ}}^2}\right)$

$\stackrel{\‾}{Q_{Wm}^j}=Q_{Wm}^j/\underset{j=1}{\overset{n}{\Σ}}{Q}_{Wm}^j,Q_{Wm}^j=Q_{W(m-1)}^j\frac{1}{\sqrt{2\mathrm{\π}\mathrm{\σ}}}\exp \left(-\frac{C_m^2}{2{\mathrm{\σ}}^2}\right)$

其中，表示m时刻第j个粒子的最终更新权值，和分别表示m时刻和m-1时刻中第j个粒子基于颜色直方图的更新权值，表示m时刻和m-1时刻中第j个粒子基于运动边缘的更新权值，表示m时刻和m-1时刻中第j个粒子基于纹理特征直方图的更新权值，A_m为m时刻中第j个粒子基于颜色直方图的观测值与真实值之间的Bhattacharrya距离，B_m为m时刻中第j个粒子基于运动边缘的观测值与真实值之间的Bhattacharrya距离,C_m为m时刻中第j个粒子基于纹理特征直方图的观测值与真实值之间的Bhattacharrya距离,σ为高斯似然模型方差，λ₁为基于颜色直方图的特征权值归一化的自适应调整因子，λ₂为基于运动边缘的特征权值归一化的自适应调整因子,λ₃为基于纹理特征直方图的特征权值归一化的自适应调整因子；

所述自适应调整因子的计算公式为：

${\mathrm{\λ}}_s^m={\mathrm{\ξ}}_{m-1}\·\[-\underset{j=1}{\overset{n}{\Σ}}\left(p_{m-1}^{s/j}\right){\log }_2^{p_{m-1}^{s/j}}\],s=1,2,3;$

其中，s＝1时，表示m时刻中基于颜色直方图的特征权值归一化的自适应调整因子，为m-1时刻中基于颜色直方图的特征值在j个粒子下的观测概率值；s＝2时，表示m时刻中基于运动边缘的特征权值归一化的自适应调整因子，为m-1时刻中基于运动边缘的特征值在j个粒子下的观测概率值；s＝3时，表示m时刻中基于纹理特征直方图的特征权值归一化的自适应调整因子，为m-1时刻中基于纹理特征直方图的特征值在j个粒子下的观测概率值；ξ_m-1表示在m-1时刻中所有粒子的空间位置方差值。

本优选实施例提出粒子观测模型的粒子权值更新公式和自适应调整因子的计算公式，对粒子的特征权值进行融合处理，有效克服了加性融合和乘性融合存在的缺陷，进一步增强了跟踪系统的鲁棒性。

在此应用场景中，选取粒子数n＝60，跟踪速度相对提高了6.5％，跟踪精度相对提高了8.4％。

应用场景4

参见图1、图2，本应用场景的一个实施例的复杂场景下的目标车辆视频跟踪系统，包括目标车辆视频采集装置1、视频稳像装置2、目标车辆追踪装置3、目标车辆位置更新装置4，所述目标车辆视频采集装置1用于采集包含目标车辆的视频；所述视频稳像装置2用于对采集的视频进行预处理，消除视频抖动的影响；所述目标车辆追踪装置3用于对视频中的所述目标车辆进行检测和跟踪，最终获得所述目标车辆的检测跟踪结果；所述目标车辆位置更新装置4用于利用所述检测跟踪结果通过在线学习更新所述目标车辆追踪装置3，进而更新所述目标车辆的位置。

优选的，所述目标车辆视频采集装置1包括高速相机11和与高速相机11连接的视频图像采集器12，所述视频图像采集器12用于采集目标车辆视频中的视频图像。

本发明上述实施例设置视频稳像装置2对采集的视频图像进行预处理，消除视频抖动的影响，从而解决了上述的技术问题。

优选的，所述对采集的视频进行预处理，包括：选定所述视频图像的第一帧图像为参考帧，并将参考帧平均划分为互不重叠的四个区域，W表示图像的宽度，H表示图像高度，四个区域大小均为0.5W×0.5H，从图像左上开始按照顺时针方向依次为区域1、2、3、4；在下一帧接收到的图像中心位置选定区域A₀，A₀的大小选定为0.5W×0.5H；将A₀按照上述方法划分为大小为0.25W×0.25H的四个图像子块A₁、A₂、A₃、A₄，A₁和A₂用于估算垂直方向上的局部运动向量，A₃和A₄用于估算水平方向上的局部运动向量，令A₁、A₂、A₃、A₄分别在1、2、3、4四个区域内搜寻最佳匹配，从而估计出视频序列的全局运动矢量，然后进行反向运动补偿，消除视频抖动的影响。

本优选实施例完善了视频稳像装置2对采集的视频图像进行预处理的功能，对视频图像进行稳像，避免了视频抖动对后续图像处理造成的影响，预处理的效率高。

优选的，所述目标车辆追踪装置3包括运动区域检测模块41、目标跟踪模块42和目标定位模块43；所述运动区域检测模块41用于在视频图像的一帧图像中检测目标车辆的运动区域D₁并以此作为目标模板；所述目标跟踪模块42用于建立粒子状态转移和观测模型并基于上述模型，采用粒子滤波预测目标车辆候选区域；所述目标定位模块43用于对所述目标车辆候选区域和所述目标模板进行特征相似度量，获得所述目标车辆的检测跟踪结果，即目标车辆的位置。

本优选实施例构建了目标车辆追踪装置3的模块架构。

优选的，所述目标跟踪模块42包括：

(1)初始化子模块421：用于在所述运动区域D₁内随机选取数量为n的粒子并对各粒子进行初始化处理，初始化处理后粒子的初始状态为x₀ⁱ，初始权值为{Q_oⁱ＝1/n,i＝1,...n}；

(2)状态转移模型建立子模块422：用于建立粒子状态转移模型，所述粒子状态转移模型采用下式：

$x_m^i={\mathrm{Ax}}_{m-1}^i+v_m^i$

式中，表示m时刻的新粒子，m≥2，为均值为0的高斯白噪声，A为4阶单位阵；m-1时刻的粒子通过状态转移模型传播；

(3)观测模型建立子模块423，用于通过颜色直方图、纹理特征直方图和运动边缘特征相结合的方式建立粒子观测模型；

(4)目标车辆候选区域计算子模块424：其利用最小方差估计来计算目标车辆候选区域：

$x_{now}=\underset{j=1}{\overset{n}{\Σ}}{Q}_m^j\·x_m^j$

式中，x_now表示计算的当前帧图像的目标车辆候选区域，表示m时刻第j个粒子的对应状态值；

(5)位置修正子模块425：用于修正异常数据：

$x_{pre}=\underset{j=1}{\overset{n}{\Σ}}{Q}_{m-1}^j\·x_{m-1}^j$

式中，x_pre表示计算的当前帧图像的目标车辆候选区域，表示m-1时刻第j个粒子的对应状态值；

设置数据异常评价函数P＝|x_now-x_pre|，若P的值大于设定的经验值T,则x_now＝x_pre；

(6)重采样子模块426：用于通过重采样操作删除权值过小的粒子，重采样时，利用系统当前时刻预测和观测的差值提供新息残差，进而通过量测新息残差对采样的粒子进行在线自适应性调整，采样过程中粒子数量和信息残差之间的关系定义为：

其中，N_m表示采样过程中m时刻的粒子数量，N_max和N_min分别表示最小和最大粒子数，N_min+1表示仅大于N_min的粒子数，N_max-1表示仅小于N_max的粒子数，表示m时刻系统的新息残差。

本优选实施例采用基于颜色直方图、纹理特征直方图和运动边缘特征相结合的方式进行采样粒子的权值更新，有效增强了跟踪系统的鲁棒性；设置位置修正子模块425，能够避免异常数据对整个系统带来的影响；在重采样子模块426中，利用当前时刻预测和观测的差值提供新息残差，进而通过量测新息残差对采样的粒子进行在线自适应性调整，并定义了采样过程中粒子数量和信息残差之间的关系，较好地保证了粒子采样的高效性和算法的实时性。

优选地，所述粒子观测模型的粒子权值更新公式为：

$Q_m^j=\frac{\stackrel{\‾}{Q_{Cm}^j}\·\stackrel{\‾}{Q_{Mm}^j}\·\stackrel{\‾}{Q_{Wm}^j}+{\mathrm{\λ}}_1\stackrel{\‾}{Q_{Cm}^j}+{{\mathrm{\λ}}_2}^2\stackrel{\‾}{Q_{Mm}^j}+{{\mathrm{\λ}}_2}^3\stackrel{\‾}{Q_{Wm}^j}+{\mathrm{\λ}}_1{\mathrm{\λ}}_2{\mathrm{\λ}}_3}{(1+{\mathrm{\λ}}_1)(1+{\mathrm{\λ}}_2)(1+{\mathrm{\λ}}_3)}$

式中

$\stackrel{\‾}{Q_{Cm}^j}=Q_{Cm}^j/\underset{j=1}{\overset{n}{\Σ}}{Q}_{Cm}^j,Q_{Cm}^j=Q_{C(m-1)}^j\frac{1}{\sqrt{2\mathrm{\π}\mathrm{\σ}}}\exp \left(-\frac{A_m^2}{2{\mathrm{\σ}}^2}\right)$

$\stackrel{\‾}{Q_{Mm}^j}=Q_{Mm}^j/\underset{j=1}{\overset{n}{\Σ}}{Q}_{Mm}^j,Q_{Mm}^j=Q_{M(m-1)}^j\frac{1}{\sqrt{2\mathrm{\π}\mathrm{\σ}}}\exp \left(-\frac{B_m^2}{2{\mathrm{\σ}}^2}\right)$

$\stackrel{\‾}{Q_{Wm}^j}=Q_{Wm}^j/\underset{j=1}{\overset{n}{\Σ}}{Q}_{Wm}^j,Q_{Wm}^j=Q_{W(m-1)}^j\frac{1}{\sqrt{2\mathrm{\π}\mathrm{\σ}}}\exp \left(-\frac{C_m^2}{2{\mathrm{\σ}}^2}\right)$

其中，表示m时刻第j个粒子的最终更新权值，和分别表示m时刻和m-1时刻中第j个粒子基于颜色直方图的更新权值，表示m时刻和m-1时刻中第j个粒子基于运动边缘的更新权值，表示m时刻和m-1时刻中第j个粒子基于纹理特征直方图的更新权值，A_m为m时刻中第j个粒子基于颜色直方图的观测值与真实值之间的Bhattacharrya距离，B_m为m时刻中第j个粒子基于运动边缘的观测值与真实值之间的Bhattacharrya距离,C_m为m时刻中第j个粒子基于纹理特征直方图的观测值与真实值之间的Bhattacharrya距离,σ为高斯似然模型方差，λ₁为基于颜色直方图的特征权值归一化的自适应调整因子，λ₂为基于运动边缘的特征权值归一化的自适应调整因子,λ₃为基于纹理特征直方图的特征权值归一化的自适应调整因子；

所述自适应调整因子的计算公式为：

${\mathrm{\λ}}_s^m={\mathrm{\ξ}}_{m-1}\·\[-\underset{j=1}{\overset{n}{\Σ}}\left(p_{m-1}^{s/j}\right){\log }_2^{p_{m-1}^{s/j}}\],s=1,2,3;$

其中，s＝1时，表示m时刻中基于颜色直方图的特征权值归一化的自适应调整因子，为m-1时刻中基于颜色直方图的特征值在j个粒子下的观测概率值；s＝2时，表示m时刻中基于运动边缘的特征权值归一化的自适应调整因子，为m-1时刻中基于运动边缘的特征值在j个粒子下的观测概率值；s＝3时，表示m时刻中基于纹理特征直方图的特征权值归一化的自适应调整因子，为m-1时刻中基于纹理特征直方图的特征值在j个粒子下的观测概率值；ξ_m-1表示在m-1时刻中所有粒子的空间位置方差值。

本优选实施例提出粒子观测模型的粒子权值更新公式和自适应调整因子的计算公式，对粒子的特征权值进行融合处理，有效克服了加性融合和乘性融合存在的缺陷，进一步增强了跟踪系统的鲁棒性。

在此应用场景中，选取粒子数n＝65，跟踪速度相对提高了6.5％，跟踪精度相对提高了8.5％。

应用场景5

参见图1、图2，本应用场景的一个实施例的复杂场景下的目标车辆视频跟踪系统，包括目标车辆视频采集装置1、视频稳像装置2、目标车辆追踪装置3、目标车辆位置更新装置4，所述目标车辆视频采集装置1用于采集包含目标车辆的视频；所述视频稳像装置2用于对采集的视频进行预处理，消除视频抖动的影响；所述目标车辆追踪装置3用于对视频中的所述目标车辆进行检测和跟踪，最终获得所述目标车辆的检测跟踪结果；所述目标车辆位置更新装置4用于利用所述检测跟踪结果通过在线学习更新所述目标车辆追踪装置3，进而更新所述目标车辆的位置。

优选的，所述目标车辆视频采集装置1包括高速相机11和与高速相机11连接的视频图像采集器12，所述视频图像采集器12用于采集目标车辆视频中的视频图像。

本发明上述实施例设置视频稳像装置2对采集的视频图像进行预处理，消除视频抖动的影响，从而解决了上述的技术问题。

优选的，所述对采集的视频进行预处理，包括：选定所述视频图像的第一帧图像为参考帧，并将参考帧平均划分为互不重叠的四个区域，W表示图像的宽度，H表示图像高度，四个区域大小均为0.5W×0.5H，从图像左上开始按照顺时针方向依次为区域1、2、3、4；在下一帧接收到的图像中心位置选定区域A₀，A₀的大小选定为0.5W×0.5H；将A₀按照上述方法划分为大小为0.25W×0.25H的四个图像子块A₁、A₂、A₃、A₄，A₁和A₂用于估算垂直方向上的局部运动向量，A₃和A₄用于估算水平方向上的局部运动向量，令A₁、A₂、A₃、A₄分别在1、2、3、4四个区域内搜寻最佳匹配，从而估计出视频序列的全局运动矢量，然后进行反向运动补偿，消除视频抖动的影响。

本优选实施例完善了视频稳像装置2对采集的视频图像进行预处理的功能，对视频图像进行稳像，避免了视频抖动对后续图像处理造成的影响，预处理的效率高。

优选的，所述目标车辆追踪装置3包括运动区域检测模块41、目标跟踪模块42和目标定位模块43；所述运动区域检测模块41用于在视频图像的一帧图像中检测目标车辆的运动区域D₁并以此作为目标模板；所述目标跟踪模块42用于建立粒子状态转移和观测模型并基于上述模型，采用粒子滤波预测目标车辆候选区域；所述目标定位模块43用于对所述目标车辆候选区域和所述目标模板进行特征相似度量，获得所述目标车辆的检测跟踪结果，即目标车辆的位置。

本优选实施例构建了目标车辆追踪装置3的模块架构。

优选的，所述目标跟踪模块42包括：

(1)初始化子模块421：用于在所述运动区域D₁内随机选取数量为n的粒子并对各粒子进行初始化处理，初始化处理后粒子的初始状态为x₀ⁱ，初始权值为{Q_oⁱ＝1/n,i＝1,...n}；

(2)状态转移模型建立子模块422：用于建立粒子状态转移模型，所述粒子状态转移模型采用下式：

$x_m^i={\mathrm{Ax}}_{m-1}^i+v_m^i$

式中，表示m时刻的新粒子，m≥2，为均值为0的高斯白噪声，A为4阶单位阵；m-1时刻的粒子通过状态转移模型传播；

(3)观测模型建立子模块423，用于通过颜色直方图、纹理特征直方图和运动边缘特征相结合的方式建立粒子观测模型；

(4)目标车辆候选区域计算子模块424：其利用最小方差估计来计算目标车辆候选区域：

$x_{now}=\underset{j=1}{\overset{n}{\Σ}}{Q}_m^j\·x_m^j$

式中，x_now表示计算的当前帧图像的目标车辆候选区域，表示m时刻第j个粒子的对应状态值；

(5)位置修正子模块425：用于修正异常数据：

$x_{pre}=\underset{j=1}{\overset{n}{\Σ}}{Q}_{m-1}^j\·x_{m-1}^j$

式中，x_pre表示计算的当前帧图像的目标车辆候选区域，表示m-1时刻第j个粒子的对应状态值；

设置数据异常评价函数P＝|x_now-x_pre|，若P的值大于设定的经验值T,则x_now＝x_pre；

(6)重采样子模块426：用于通过重采样操作删除权值过小的粒子，重采样时，利用系统当前时刻预测和观测的差值提供新息残差，进而通过量测新息残差对采样的粒子进行在线自适应性调整，采样过程中粒子数量和信息残差之间的关系定义为：

其中，N_m表示采样过程中m时刻的粒子数量，N_max和N_min分别表示最小和最大粒子数，N_min+1表示仅大于N_min的粒子数，N_max-1表示仅小于N_max的粒子数，表示m时刻系统的新息残差。

本优选实施例采用基于颜色直方图、纹理特征直方图和运动边缘特征相结合的方式进行采样粒子的权值更新，有效增强了跟踪系统的鲁棒性；设置位置修正子模块425，能够避免异常数据对整个系统带来的影响；在重采样子模块426中，利用当前时刻预测和观测的差值提供新息残差，进而通过量测新息残差对采样的粒子进行在线自适应性调整，并定义了采样过程中粒子数量和信息残差之间的关系，较好地保证了粒子采样的高效性和算法的实时性。

优选地，所述粒子观测模型的粒子权值更新公式为：

$Q_m^j=\frac{\stackrel{\‾}{Q_{Cm}^j}\·\stackrel{\‾}{Q_{Mm}^j}\·\stackrel{\‾}{Q_{Wm}^j}+{\mathrm{\λ}}_1\stackrel{\‾}{Q_{Cm}^j}+{{\mathrm{\λ}}_2}^2\stackrel{\‾}{Q_{Mm}^j}+{{\mathrm{\λ}}_2}^3\stackrel{\‾}{Q_{Wm}^j}+{\mathrm{\λ}}_1{\mathrm{\λ}}_2{\mathrm{\λ}}_3}{(1+{\mathrm{\λ}}_1)(1+{\mathrm{\λ}}_2)(1+{\mathrm{\λ}}_3)}$

式中

$\stackrel{\‾}{Q_{Cm}^j}=Q_{Cm}^j/\underset{j=1}{\overset{n}{\Σ}}{Q}_{Cm}^j,Q_{Cm}^j=Q_{C(m-1)}^j\frac{1}{\sqrt{2\mathrm{\π}\mathrm{\σ}}}\exp \left(-\frac{A_m^2}{2{\mathrm{\σ}}^2}\right)$

$\stackrel{\‾}{Q_{Mm}^j}=Q_{Mm}^j/\underset{j=1}{\overset{n}{\Σ}}{Q}_{Mm}^j,Q_{Mm}^j=Q_{M(m-1)}^j\frac{1}{\sqrt{2\mathrm{\π}\mathrm{\σ}}}\exp \left(-\frac{B_m^2}{2{\mathrm{\σ}}^2}\right)$

$\stackrel{\‾}{Q_{Wm}^j}=Q_{Wm}^j/\underset{j=1}{\overset{n}{\Σ}}{Q}_{Wm}^j,Q_{Wm}^j=Q_{W(m-1)}^j\frac{1}{\sqrt{2\mathrm{\π}\mathrm{\σ}}}\exp \left(-\frac{C_m^2}{2{\mathrm{\σ}}^2}\right)$

其中，表示m时刻第j个粒子的最终更新权值，和分别表示m时刻和m-1时刻中第j个粒子基于颜色直方图的更新权值，表示m时刻和m-1时刻中第j个粒子基于运动边缘的更新权值，表示m时刻和m-1时刻中第j个粒子基于纹理特征直方图的更新权值，A_m为m时刻中第j个粒子基于颜色直方图的观测值与真实值之间的Bhattacharrya距离，B_m为m时刻中第j个粒子基于运动边缘的观测值与真实值之间的Bhattacharrya距离,C_m为m时刻中第j个粒子基于纹理特征直方图的观测值与真实值之间的Bhattacharrya距离,σ为高斯似然模型方差，λ₁为基于颜色直方图的特征权值归一化的自适应调整因子，λ₂为基于运动边缘的特征权值归一化的自适应调整因子,λ₃为基于纹理特征直方图的特征权值归一化的自适应调整因子；

所述自适应调整因子的计算公式为：

${\mathrm{\λ}}_s^m={\mathrm{\ξ}}_{m-1}\·\[-\underset{j=1}{\overset{n}{\Σ}}\left(p_{m-1}^{s/j}\right){\log }_2^{p_{m-1}^{s/j}}\],s=1,2,3;$

其中，s＝1时，表示m时刻中基于颜色直方图的特征权值归一化的自适应调整因子，为m-1时刻中基于颜色直方图的特征值在j个粒子下的观测概率值；s＝2时，表示m时刻中基于运动边缘的特征权值归一化的自适应调整因子，为m-1时刻中基于运动边缘的特征值在j个粒子下的观测概率值；s＝3时，表示m时刻中基于纹理特征直方图的特征权值归一化的自适应调整因子，为m-1时刻中基于纹理特征直方图的特征值在j个粒子下的观测概率值；ξ_m-1表示在m-1时刻中所有粒子的空间位置方差值。

本优选实施例提出粒子观测模型的粒子权值更新公式和自适应调整因子的计算公式，对粒子的特征权值进行融合处理，有效克服了加性融合和乘性融合存在的缺陷，进一步增强了跟踪系统的鲁棒性。

在此应用场景中，选取粒子数n＝70，跟踪速度相对提高了6％，跟踪精度相对提高了9％

最后应当说明的是，以上应用场景仅用以说明本发明的技术方案，而非对本发明保护范围的限制，尽管参照较佳应用场景对本发明作了详细地说明，本领域的普通技术人员应当理解，可以对本发明的技术方案进行修改或者等同替换，而不脱离本发明技术方案的实质和范围。