一种风电场风速的多步预测方法及系统与流程

本发明涉及预测学技术领域，更具体的说，是涉及一种风电场风速的多步预测方法及系统。

背景技术：

在现有技术中，预测学现已广泛应用于国民经济各部门以及社会、科技、军事、政治等领域，成为管理决策不可缺少的重要组成部分。同样对于风电机组而言，由于风能具有间歇性、不可控性和波动性等特点，极大影响了电力系统的发电质量、安全性和稳定性，因而对风速进行准确的预测是实现电网合理调度运行的有效手段，提供风速预测的精度具有很重要的现实意义。

目前，风电场风速预测主要包括：迭代预测模型和单纯基于历史数据的预测模型以及将“多输出模型”与“单纯基于历史数据的预测模型”结合起来的预测模型来对进行风速进行直接的多步预测。对于迭代式预测模型，该模型在一些预测中取得了不错的效果，该模型通过将预测值不断地加入到预测模型中来扩充预测模型的样本，从而达到迭代的效果，但每一步产生的误差会向后传递，造成误差的累积，预测步数越多，累积的误差越大；单纯基于历史数据的预测模型，该方法通过模型用同一组历史数据对接下来的几个风速点进行预测，在预测过程中没有引入估计值，即没有累积误差，但这种预测方法没有考虑到时间序列内在的相关性或者说内部的混沌特性，若产生线性或者轻微非线性的模型会对时间序列的混沌性造成破坏；另外就是将以上两种方法组合到一起的预测模型，同基于历史数据的预测模型一样，运用不同模型对每一步进行预测，而且每一步预测中都加入前几步的预测值，这种方法同样无法避免误差累积对结果的影响。

因此，提供一种可以解决上述几种风电场风速预测方法带来的问题，是本领域技术人员亟待解决的技术问题。

技术实现要素：

有鉴于此，本发明提供了一种风电场风速的多步预测方法及系统，以解决现有技术中采用迭代预测模型和将“多输出模型”与“单纯基于历史数据的预测模型”结合起来的预测模型的方法进行风电场风速的预测产生的迭代误差的问题。

为实现上述目的，本发明提供如下技术方案：

一种风电场风速的多步预测方法，该方法基于并行相关向量机，该方法包括：

构建预测模型，得到目标值与特征向量之间的关系；

根据CAO计算方法确定所述目标值的嵌入维数m；

将每组的所述训练样本的最后m个样本作为特征向量输入所述预测模型中进行相关向量机的计算，得到每组所述训练样本的特征向量对应的预测值；

将所述每组所述训练样本的特征向量对应的预测值进行排序得到多步预测结果。

其中，所述构建预测模型包括：

对训练样本构造样本特征，所述训练样本为原始风速时间序列；

对所述训练样本的各个样本特征向量与目标值的对应关系进行整合，得到所述训练样本的特征，即得到目标值与特征向量之间的关系。

其中，所述对训练样本构造样本特征，所述训练样本为原始风速时间序列包括：

将原始风速时间序列按照预设时间间隔进行分组，得到所述预设时间间隔个分组序列；

采用相空间重构理论分别对所述预设时间间隔个分组序列进行分析，得到所述分组序列与目标值之间的关系。

其中，所述将每组的所述训练样本的特征输入所述预测模型中进行相关向量机的计算，得到每组的所述训练样本的特征对应的预测值包括：

分别对每组时间序列进行样本训练，建立相关向量机预测模型；

将每组的所述训练样本的最后m个样本作为特征向量输入所述预测模型中计算得到每组的所述训练样本的特征向量对应的预测值。

一种风电场风速的多步预测系统，该系统基于并行相关向量机，该系统包括：

模型构建单元，用于构建预测模型，得到目标值与特征向量之间的关系；

第一计算单元，用于根据CAO计算方法确定所述目标值的嵌入维数m；

第二计算单元，用于将每组的所述训练样本的最后m个样本作为特征向量输入所述预测模型中进行相关向量机的计算，得到每组所述训练样本的特征向量对应的预测值；

排序单元，用于将所述每组所述训练样本的特征向量对应的预测值进行排序得到多步预测结果。

其中，所述模型构建单元包括：

构造单元，用于对训练样本构造样本特征，所述训练样本为原始风速时间序列；

整合单元，用于对所述训练样本的各个样本特征向量与目标值的对应关系进行整合，得到所述训练样本的特征，即得到目标值与特征向量之间的关系。

其中，所述构造单元包括：

分组单元，用于将原始风速时间序列按照预设时间间隔进行分组，得到所述预设时间间隔个分组序列；

分析单元，用于采用相空间重构理论分别对所述预设时间间隔个分组序列进行分析，得到所述分组序列与目标值之间的关系。

其中，所述第二计算单元包括：

样本训练单元，用于分别对每组时间序列进行样本训练，建立相关向量机预测模型；

计算子单元，用于将每组的所述训练样本的最后m个样本作为特征向量输入所述预测模型中计算得到每组的所述训练样本的特征向量对应的预测值。

经由上述的技术方案可知，与现有技术相比，本发明公开了一种风电场风速的多步预测方法及系统，本方法及系统基于并行相关向量机，具体该方法包括：构建预测模型，得到目标值与特征向量之间的关系；根据CAO计算方法确定所述目标值的嵌入维数m；将每组的训练样本的最后m个样本作为特征向量输入预测模型中进行相关向量机的计算，得到每组训练样本的特征向量对应的预测值；将每组训练样本的特征向量对应的预测值进行排序得到多步预测结果。本发明通过对原始风速时间序列分为多个组，再通过相空间重构得到的时间延迟对风速序列进行重构，对每组风速序列进行相关向量机预测，且每组风速序列逻辑上为并列关系，相互之间不会发生影响，避免了现有技术中迭代法产生的迭代误差，保证了预测精度的同时大大提高了预测步长。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据提供的附图获得其他的附图。

图1为本发明实施例提供的一种风电场风速的多步预测方法流程示意图；

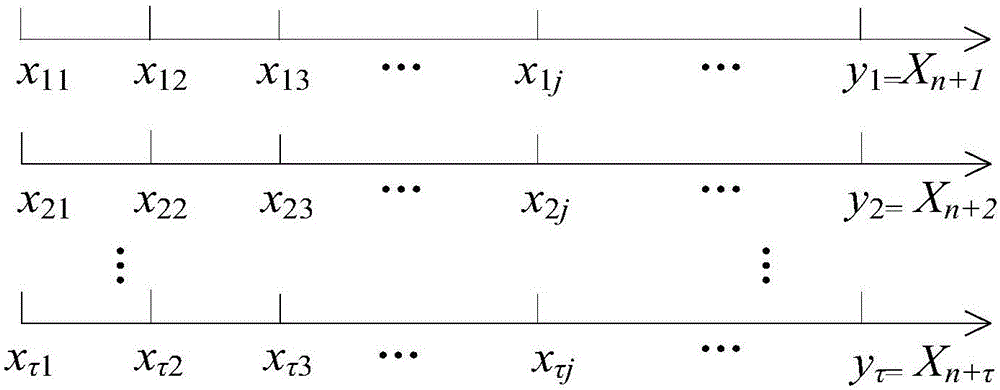
图2为本发明实施例中时间序列并行多步预测结果示意图；

图3为本发明实施例提供的一种风电场风速的多步预测系统结构示意图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

本文提出的“基于并行相关向量机(P-RVM)的多步预测方法”提到的相关概念解释如下。

“并行”是指通过向空间重构将风速时间序列分为τ组，组与组之间是并列并且同时进行的预测，即所谓的“并行”；

“相关向量机”是指相关向量机(RVM)是通过核函数映射把数据由低维向高维空间的转化，相关向量机的训练是基于贝叶斯理论，在先验分布的条件下，利用自动相关决策理论(Automatic Relevance Determination，ARD)来消除无关联的点，从而获得稀疏化的分类模型。

核函数：RVM是一种基于核的算法。核函数的定义为设X是Rn中的一个子集，如果存在着从X到某个Hilbert空间H的映射：使得其中(·)表示内积，称定义在X×X上的函数K(x,x^/)是核函数。

核函数的作用就是把来自低维空间里的两个向量进行某种变换，从而能够计算出他们在高维空间里的向量内积值。

多步预测：进行一次预测可以产生在时间序列上顺序排列的多个预测值的预测过程称为多步预测，而单步预测则一次只产生一个预测值。由于多步预测的方法较多，产生的效果一样，但过程不一样。比如迭代预测是每迭代一次产生一次预测值，需要多次迭代才可以产生多步预测的效果；多输出模型，由于模型的特点，可一次输出多个预测值；而本文所提出的方法是通过τ个并行的风速序列，每组建立RVM模型，每组产生一个预测值从而产生步长为τ的多步预测效果，因此多步预测并不是只通过一步预测就可以产生多个预测值，这还与采取的预测方法有关。

时间延迟：在本专利中利用时间延迟作为风速时间序列所分的并行组数的度量。

嵌入维数：在本专利中利用嵌入维数作为样本特征的度量，用来构造样本条件特征值，并使其与目标值对应。

采用Cao方法来对嵌入维数m进行计算，并将m作为特征维数，得到样本特征。以时间序列x_i(i＝1，2，…，τ)为例，构造样本条件特征值，并与目标值对应：

Cao方法是学者Liangyue Cao提出的主要用来求取时间序列嵌入维数的方法，还可以用于时间序列混沌特性的分析。Cao方法可以依照一下步骤实现。

在m维空间中，每一个相点矢量为X(i)＝{x(i)，x(i+τ)，.…x(i+(m-1)τ)}，都有一个某距离内最临近点X^NN(i)，其距离为R_m(i)，则R²_m(i)＝||X(i)-X^NN(i)||²。

当向空间的维数增加到m+1维时，这两个相点的距离就会发生变化，两者距离变成为R_m+1(i)，由m增加1而引起的两临近点间距离变化是[R²_m+1(i)-R²_m(i)]^1/2＝|x(i+τm)-x^NN(i+τm)|可见，如果两临近点的距离不随m增大而增大，即R_m(i)＝R_m+1(i)，则邻近点是真实的；如果R_m+1(i)比R_m(i)大很多，可以认为这是由于高维混沌吸引子中两个不相邻的点投影到低维轨道上时变成相邻的两个点造成的，因此这样的邻点是虚设的。定义其中X_m(i)和X_m^NN(i)为m维空间的第i个向量和它的最邻近点，X_m+1(i)和X_d+1^NN(i)为m+1维空间的第i个向量和它的最邻近点。

定义E₁(m)＝E(m+1)/E(m),如果时间序列是确定的，则嵌入维数是存在的，即E₁(m)将在m大于某一特定值m₀时不再变化。若时间序列是随机信号，则E₁(m)应逐渐增加，但在实际应用中不容易判断有现场序列E₁(m)究竟是在缓慢变化还是已经稳定，因此补充一个判断准则：

$E^{*}\left(m\right)=\frac{1}{N-m\mathrm{\τ}}\underset{i=1}{\overset{N-m\mathrm{\τ}}{\Σ}}|x(i+\mathrm{\τ}m)-x^{NN}(i+\mathrm{\τ}m)|$

E₂(m)＝E*(m+1)/E*(m)

对于随机序列，数据之间没有相关性，即不具备可与测性，E₂(m)始终为1；对于确定序列，数据之间的相关关系是依赖于嵌入维数m值变化的，总存在一些m值使得E₂(m)不等于1。

请参阅附图1，图1为本发明实施例提供的一种风电场风速的多步预测方法流程示意图。如图1所示，本发明公开了一种风电场风速的多步预测方法，该方法基于并行相关向量机，该方法包括如下具体流程：

S101、构建预测模型，得到目标值与特征向量之间的关系。

在本实施例中，构建预测模型的具体步骤如下：

对训练样本构造样本特征，训练样本为原始风速时间序列。

需要说明的是，该步骤可以具体为：

将原始风速时间序列按照预设时间间隔进行分组，得到预设时间间隔个分组序列；

采用相空间重构理论分别对预设时间间隔个分组序列进行分析，得到分组序列与目标值之间的关系。

对训练样本的各个样本特征与目标值的对应关系进行整合，得到训练样本的特征，即得到预测值与其样本特征之间的关系。

具体说明的是：

基于并行相关向量机的多步预测模型建立：

对于时间序列X＝{X1,X2,…,Xn}，Xi分别为第i个时刻对应的风速值，基于并行RVM多步预测的模型建立具体步骤如下：

首先，确定时间延迟τ。从风场风速数据中选取合适数目的一组风速数据并分析其混沌特性，通过互信息法计算时间延迟τ。

其次，利用τ将数据分组。以τ作为时间间隔将时间样本进行分组，最终将样本分为τ组。如下所示。

x1＝{x11,x12,…}＝{X1,X1+τ,…}；

x2＝{x21,x22,…}＝{X2,X2+τ,…}；

…

xτ＝{xτ1,xτ2,…}＝{Xτ,Xτ+τ,…}；

然后，分别针对τ组数据建立τ个RVM预测模型。

利用相空间重构理论对分别对τ组训练样本进行分析，得到训练样本的特征，从而得到目标值与特征向量之间的关系。

步骤S102、根据CAO计算方法确定目标值的嵌入维数m。

根据CAO方法计算求得嵌入维数m，即：

(x_i1,x_i2，…，x_im)→(x_i(m+1))

(x_i2,x_i3，…，x_i(m+1))→(x_i(m+2))

…

(x_ij，x_i(j+1)，…，x_i(j+m-1))→(x_i(j+m))

…

其中，左侧为样本条件特征向量，右侧为对应目标值。即得到第i个时间序列的训练样本，根据确定的风速数据进行模型的训练，将左侧样本条件特征向量输入到训练模型中即可得到右侧对应目标值。根据这个进行RVM进行预测模型的建立。

基于训练样本x_i，利用RVM方法建立预测模型。具体步骤如下：

建立预测模型，分别对每组时间序列进行样本训练，建立RVM预测模型。

首先，设定目标值t_i与条件特征值{x_i}_i＝1^N、权重系数w_i存在的函数关系

t_i＝y(x_i,w)+ε_i

$y(x_i,w)={\Σ}_{i=1}^N{w}_{i}k(x,x^{/})+w_0$

式中，x_i与t_i分别是上述的样本条件特征值与其对应的目标值、w_i为权重系数、目标函数带有噪声且满足ε_i～N(0,σ²)，w_i为权重系数，k(x，x^/)为核函数，N为样本数量。

其次，将条件特征值{x_i}_i＝1^N与目标值t_i代入到核函数矩阵：

由上述公式t_i＝y(x_i,w)+ε_i可知，求得t_i服从t_i～(y(x_i,w),σ²)的分布。对于相互独立的目标值t＝[t₁,t₂,…,t_n]^T、w_i与σ²已知的条件下，训练集的似然估计如下：

$p\left(t\right|w,{\mathrm{\σ}}^2)={\left(2{\mathrm{\π\σ}}^2\right)}^{-N/2}\exp (-\frac{\left|\right|t-\mathrm{\Φ}w|{|}^2}{2{\mathrm{\σ}}^2})$

式中，t＝(t₁,t₂,…,t_N)’，w＝(w₁,w₂,…w_N)’，Φ是由特征向量代入到核函数中的N×(N+1)维矩阵：

再次，引入超参数向量，将求解权重w_i的问题转化为对超参数向量的求解：

采用稀疏贝叶斯原理对w赋予零均值高斯先验分布得：

$p\left(w\right|\mathrm{\α})=\underset{i=0}{\overset{N}{\Π}}N\left(w_i\right|0,{\mathrm{\α}}_i^{-1})$

式中，α＝[α₁,α_2,…,α_n]^T是N+1维超参数向量，每一个权重对应一个独立的超参数分量，因此将求解权重w_i的问题转化为对α_i的求解，并且保证了RVM的稀疏性。

然后，求解超参数α和方差σ²：

在定义了先验概率分布及似然分布以后，根据贝叶斯原理，就以求得所有未知参数的后验概率分布为：

$p\left(w\right|t,\mathrm{\α},{\mathrm{\σ}}^2)={\left(2\mathrm{\π}\right)}^{-\frac{(N+1)}{2}}{|\Σ|}^{-\frac{1}{2}}\{-\frac{1}{2}{(w-\mathrm{\μ})}^T{\Σ}^{-1}(w-\mathrm{\μ})\}$

式中，Σ＝(σ^-2Φ^TΦ+A)^-1，μ＝σ^-2ΣΦ^Tl，A＝diag(α₁,α₂,…,α_N)。使用最大似然法可得超参数α和方差σ²。

最后，得到目标值t_i与条件特征值{x_i}_i＝1^N、权重系数w_i的预测模型

t_i＝y(x_i,w)+ε_i

S103、将每组的训练样本的最后m个样本作为特征向量输入预测模型中进行相关向量机的计算，得到每组训练样本的特征向量对应的预测值。

在本实施例中，该步骤可以具体为：

分别对每组时间序列进行样本训练，建立相关向量机预测模型；

将每组的训练样本的最后m个样本作为特征向量输入预测模型中计算得到每组训练样本的特征向量对应的预测值，即：具体的，其实模型建立的过程是将每组时间序列得到的样本条件特征向量与目标值之间的对应关系输入到RVM中，让其进行训练，构建预测模型；预测的过程是通过将每组序列的最后m个风速数据作为特征向量输入到经过训练后的RVM，得到第m+1个风速值，这个风速值就是预测值。

S104、将每组训练样本的特征向量对应的预测值进行排序得到多步预测结果。

通过上述具体的建立模型的方法，通过对训练样本(x_i)构造样本特征，再对训练样本(x_i)各个样本特征向量与目标值的对应关系进行整合，得到训练样本(x_i)的特征，即为，得到预测值与其样本特征之间的关系。

分别将每组训练样本最后m个风速数据作为特征向量输入到RVM预测模型中，从而每组分别得到各自的预测值，即可以确定第m+1的风速值，实现对风速的准确预测。

利用每个时间序列整合的样本特征，得到每个时间序列的预测值y_i，对τ组的预测值进行有序的排列最终形成多步预测的预测结果，如附图2中所示(y₁、y₂、…y_τ即为多步预测结果)。

本发明中，在并行的多个RVM中，每个RVM模型都相当于一步预测，即通过重构的历史数据对下一个时间点的风速值进行预测，从而避免了迭代法中预测值的加入导致的迭代误差；另外，本方法充分考虑到风速序列的混沌性，通过计算时间序列时间延迟τ(即为预测步长)，利用该参数对原始时间序列模型进行重构，从而形成τ个并行的风速时间序列，从而避免了直接法对时间序列混沌特性的破坏；最后，嵌入维数确定了特征向量，将嵌入维数作为特征维数，得到样本特征，同样避免了对混沌特性的破坏。因此，与传统的多步预测模型相比，本发明提出的基于并行相关向量机的多步预测方法预测精度更高。

在上述公开的方法的基础上，本发明还公开了一种系统。

请参阅附图3，图3为本发明实施例提供的一种风电场风速的多步预测系统结构示意图。如图3所示，本发明实施例公开了一种风电场风速的多步预测系统，该系统基于并行相关向量机，该系统具体结构包括：

模型构建单元301，用于构建预测模型，得到目标值与特征向量之间的关系；

第一计算单元302，用于根据CAO计算方法确定所述目标值的嵌入维数m；

第二计算单元303，用于将每组的训练样本的最后m个样本作为特征向量输入预测模型中进行相关向量机的计算，得到每组训练样本的特征向量对应的预测值；

排序单元304，用于将每组训练样本的特征向量对应的预测值进行排序得到多步预测结果。

优选的，所述模型构建单元301包括：

构造单元，用于对训练样本构造样本特征，训练样本为原始风速时间序列；

整合单元，用于对训练样本的各个样本特征向量与目标值的对应关系进行整合，得到训练样本的特征，即得到目标值与特征向量之间的关系。

优选的，所述构造单元包括：

分组单元，用于将原始风速时间序列按照预设时间间隔进行分组，得到预设时间间隔个分组序列；

分析单元，用于采用相空间重构理论分别对预设时间间隔个分组序列进行分析，得到分组序列对应的特征向量与目标值之间的关系。

优选的，所述第二计算单元303包括：

样本训练单元，用于分别对每组时间序列进行样本训练，建立相关向量机预测模型；

计算子单元，用于将每组的训练样本的最后m个样本作为特征向量输入预测模型中计算得到每组的训练样本的特征向量对应的预测值。

本发明中，在并行的多个RVM中，每个RVM模型都相当于一步预测，即通过重构的历史数据对下一个时间点的风速值进行预测，从而避免了迭代法中预测值的加入导致的迭代误差；另外，本方法充分考虑到风速序列的混沌性，通过计算时间序列时间延迟τ(即为预测步长)，利用该参数对原始时间序列模型进行重构，从而形成τ个并行的风速时间序列，从而避免了直接法(直接预测策略是指通过历史观测数据独立的进行每一步预测，每一步之间没有影响)对时间序列混沌特性的破坏；最后，嵌入维数确定了特征向量，将嵌入维数作为特征维数，得到样本特征，同样避免了对混沌特性的破坏。因此，与传统的多步预测模型相比，本发明提出的基于并行相关向量机的多步预测方法预测精度更高。

综上所述，本发明公开了一种风电场风速的多步预测方法及系统，本方法基于并行相关向量机，该方法包括：构建预测模型，得到目标值与特征向量之间的关系；根据CAO计算方法确定所述目标值的嵌入维数m；将每组的训练样本的最后m个样本作为特征向量输入预测模型中进行相关向量机的计算，得到每组训练样本的特征向量对应的预测值；将每组训练样本的特征向量对应的预测值进行排序得到多步预测结果。本发明通过对原始风速时间序列分为多个组，再通过相空间重构得到的时间延迟对风速序列进行重构，对每组风速序列进行相关向量机预测，且每组风速序列逻辑上为并列关系，相互间不会发生影响，避免了现有技术中迭代法产生的迭代误差，保证预测精度的同时大大提高了预测步长。

需要说明的是，本说明书中的各个实施例均采用递进的方式描述，每个实施例重点说明的都是与其他实施例的不同之处，各个实施例之间相同相似的部分互相参见即可。

以上结合附图对本发明所提出的方法进行了示例性描述，以上实施例的说明只是用于帮助理解本发明的核心思想。对于本领域的一般技术人员，依据本发明的思想，在具体实施方式及应用范围上均会有改变之处。综上所述，本说明书内容不应理解为对本发明的限制。

对所公开的实施例的上述说明，使本领域专业技术人员能够实现或使用本发明。对这些实施例的多种修改对本领域的专业技术人员来说将是显而易见的，本文中所定义的一般原理可以在不脱离本发明的精神或范围的情况下，在其它实施例中实现。因此，本发明将不会被限制于本文所示的这些实施例，而是要符合与本文所公开的原理和新颖特点相一致的最宽的范围。