一种深度生成网络随机训练算法及装置的制作方法

本发明涉及机器学习领域，具体涉及一种深度生成网络随机训练算法及装置。

背景技术：

深度生成网络用多层的结构去刻画数据的分布，其每一层都经过一些非线性的转换。在众多的需要随机性以及概率推理的任务中，例如图像生成、数据补全等，深度生成网络取得了广泛的应用。随着一些判别性的特征加入，深度生成网络在分类、预测等问题上存在的性能不足也得到了明显的改善。

在众多深度生成模型的例子中，Goodfellow等人在2015年提出了generative adversarial network(GAN)，其模拟了一个博弈游戏用来生成数据。然而其优化目标为一个最大-最小问题，通常而言其难以训练。在同期，Li等人提出了Generative Moment Matching Network(GMMN)，其从一个简单地分布中采样，例如均匀分布，之后通过网络传播获得一个样本。与GAN不同的是，GMMN是将目标概率嵌入到某个再生核希尔伯特空间中，其优化目标可以归结为使得在此空间中的两个元素之间的差异最小(在范数意义下)，此准则被称为Maximum Mean Discrepancy(MMD)。通过核技巧，此优化目标具有简单的形式，进而通过梯度随机下降结合后向传播即可完成训练。

虽然GMMN在非监督的数据生成上取得了成功，但是其只能应用在此。对于更加广泛的问题，例如分类、预测问题，以及根据不同的条件变量生成数据等问题，由于GMMN训练目标中不包含条件变量，所以其不能应用在此。与之相对的GAN可以很容易地扩展成基于条件变量的版本，因此GMMN的相对狭小的应用范围限制了其影响力。然而，对于概率在希尔伯特空间中的嵌入问题，Song等人在2009年就做出了对于条件概率嵌入的研究。与MMD不同，单个概率分布的嵌入是希尔伯特空间的一个元素，而条件概率的嵌入可以理解为希尔伯特空间之间的算子。这种扩展的技术对GMMN的扩展提供了借鉴意义。

上述领域的最新成果为采用条件最大矩匹配作为训练准则的条件深度生成网络的提出打下了坚实的基础。然而这些技术并不能使得之前的基于矩匹配的深度生成网络应用于诸如依据条件生成数据以及分类问题等。

因此，如何扩展基于矩匹配的深度生成模型的应用范围，使之能够应用于多样的任务例如根据类别的图像生成、数据分类、贝叶斯网络的指示提取等，具有十分重要的意义。

技术实现要素：

针对现有技术中的缺陷，本发明提供一种深度生成网络随机训练算法及装置。

一方面，本发明提出一种深度生成网络随机训练算法，包括：

输入包括条件变量以及生成数据本身的数据集合；

将所述数据集合随机分割成包括一定数量样本的若干批次；

对各批次的样本数据通过梯度后向传播进行参数更新并输出所述参数；

其中，所述对各批次的样本数据通过梯度后向传播进行参数更新包括使用条件极大矩匹配准则。

本发明提出的深度生成网络随机训练算法，由于在对样本数据的处理过程中使用了条件极大矩匹配准则，所述条件极大矩匹配准则是对MMD的拓展，因此，可扩展基于矩匹配的深度生成模型的应用范围。

另一方面，本发明还提出一种深度生成网络随机训练装置，包括：

输入单元，用于输入包括条件变量以及生成数据本身的数据集合；

分割单元，用于将所述数据集合随机分割成包括一定数量样本的若干批次；

训练单元，用于对各批次的样本数据通过梯度后向传播进行参数更新并输出所述参数；

其中，所述对各批次的样本数据通过梯度后向传播进行参数更新包括使用条件极大矩匹配准则。

本发明提出的深度生成网络随机训练装置，由于在对样本数据的处理过程中使用了条件极大矩匹配准则，所述条件极大矩匹配准则是对MMD的拓展，因此，可扩展基于矩匹配的深度生成模型的应用范围。

附图说明

图1为深度生成网络的结构示意图；

图2为本发明深度生成网络随机训练算法实施例的流程示意图；

图3为本发明深度生成网络随机训练装置实施例的结构示意图。

具体实施方式

为使本发明实施例的目的、技术方案和优点更加清楚，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

图1为深度生成网络的结构示意图，参看图3，需要说明的是，对于深度生成网络而言，其训练是反向的，即从输出层开始通过梯度反向传播。对于生成网络而言，其输入是条件变量以及隐式变量的向量组(x,h)，所述隐式变量h通过采样获得，其作用是对生成数据的隐层编码。所述条件变量与所述隐式变量通过例如向量的拼接实现链接从而形成网络的输入层。

网络的中间层通常是全连接层(MLP)或者卷积层(CNN)。网络层间需要非线性转换，因此，可选择ReLu作为网络数据的非线性转换器。

输入通过网络传播，最终生成数据y。算法的输出为模型参数w，其包含网络的全部参数。对于深度生成网络而言，每一层都具有其自身的参数，例如，对于全连接层(MLP)而言，其输入x和输出y的关系为y＝relu(Wx+b)，则其参数为(W，b)。每一层参数汇总则可得模型参数w。

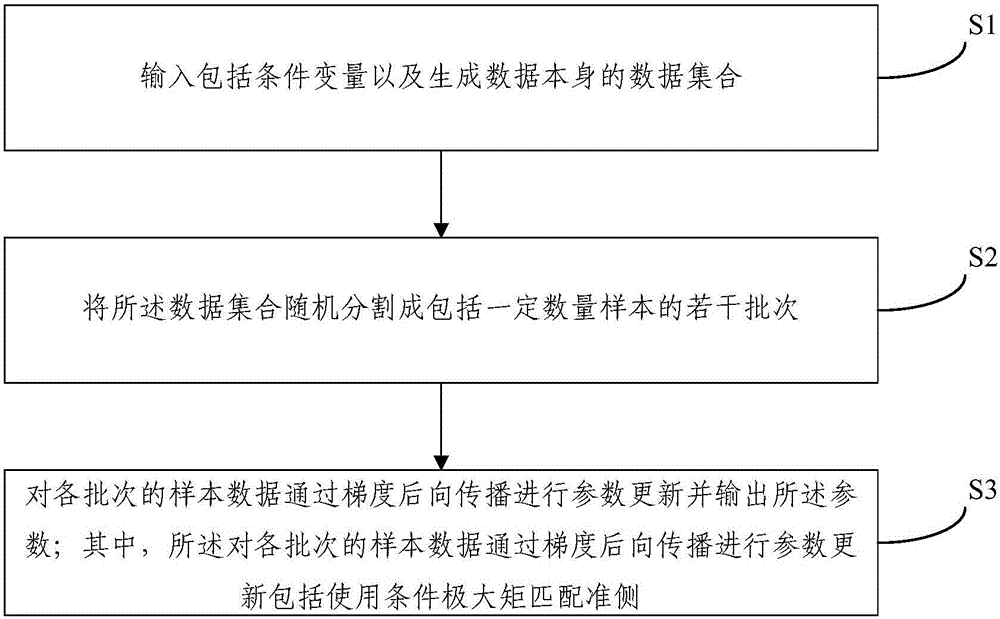
图2为本发明深度生成网络随机训练算法实施例的流程示意图，参看图1，本实施例公开一种生成网络随机训练算法，包括：

S1、输入包括条件变量以及生成数据本身的数据集合；

S2、将所述数据集合随机分割成包括一定数量样本的若干批次；

S3、对各批次的样本数据通过梯度后向传播(back-propagation)进行参数更新并输出所述参数；其中，所述对各批次的样本数据通过梯度后向传播进行参数更新包括使用条件极大矩匹配准则。

本发明提出的深度生成网络随机训练算法，由于在对样本数据的处理过程中使用了条件极大矩匹配准则，所述条件极大矩匹配准则是对MMD的拓展，因此，可扩展基于矩匹配的深度生成模型的应用范围。

具体地，在步骤S1中，输入数据为数据集合；例如输入数据集合其中，x_i为条件变量，y_i为生成数据本身；例如，对于一张被标记为类别A的图片，A即为条件变量x_i，图片为生成数据本身y_i。

在步骤S2中，每次可从数据集合中随机用一个批次来近似整个数据集。所述批次的样本数量可根据数据集合的结构选取，具体地，对于结构简单的数据集，各批次包括的样本个数可以偏小，例如100-200。对于结构相对复杂的数据集，各批次的样本个数可适当增加。

步骤S3包括如下步骤：

S31、随机从输入数据集合D中选择一个批次B，对于任一x∈B，生成一个样本y；记B’为生成的数据集合(x,y)；

具体地，对于任一x∈B，其会与通过采样获得的隐式变量h组成向量组(x，h)。所述向量组通过网络传播生成样本y。

S32、根据B与B’计算条件极大矩匹配准则

S33、获取所述条件极大矩匹配准则关于参数的导数并以所述条件极大矩匹配准则关于参数的导数作为输出层的梯度；

S34、根据链式求导法则获取各中间层的梯度；

S35、对所述参数w通过梯度下降算法进行更新；

S36、重复步骤S31-S35直至所述参数w满足收敛条件后，输出所述参数w。

具体地，所述条件极大矩匹配准则(Conditional Maximum Mean Discreoancy，CMMD)包括：比较两个再生核希尔伯特空间之间算子的差异，以判断两个条件概率之间的差距。

具体地，所述条件极大矩匹配准则是MMD的推广，其通过比较两个再生核希尔伯特空间之间的算子的差异，以判断两个条件概率之间的差距。例如，设条件随机变量X，其对应的再生核希尔伯特空间为F；设另外两个条件随机变量Y，Z，两者对应的再生核希尔伯特空间都为G，则两个条件概率分别为P(Y|X)以及P(Z|X)。为对比上述两个条件概率，先将所述两个条件概率嵌入到希尔伯特空间中，可得两个希尔伯特空间之间的算子C_Y|X与C_Z|X，其也可看作是两个希尔伯特空间张量积形成的空间里的一个元素。所述条件极大矩匹配准则对比两个嵌入之间在空间所装备的范数意义下的差距：

$L_{CMMD}^2=\left|\right|C_{Y|X}-C_{Z|X}|{|}_{F\⊗G}^2$

实际应用中，设两个数据集与则可以比较两个概率嵌入估计的差值以近似L_CMMD：

${\hat{L}}_{CMMD}^2=\left|\right|{{\hat{C}}^s}_{Y|X}-{{\hat{C}}^d}_{Y|X}|{|}_{F\⊗G}^2$

其中，与分别是由两个数据集(即训练数据集与模型生成的数据集)生成的经验估计。一般地，条件概率的嵌入是无穷维的，但是通过核技巧，上述目标可以通过Kernel Gram矩阵高效地计算出来。对于连续变量，可选取高斯核函数；对于离散变量，可选择Delta核函数。具体地，核技巧通过将无线维的内积运算通过核函数准确地计算出来，因此有着可以实际计算的形式：

${\hat{L}}_{CMMD}^2=Tr(L_d\·C_1)+Tr(L_s\·C_2)+Tr(L_{ds}\·C_3)$

其中L是输出变量的Gram矩阵，C是由训练数据确定的参数矩阵。

在完成对当前批次的随机训练后，则重复上述步骤，直至完成对所述数据集合内的所有批次的随机训练。

本发明提供的深度生成网络随机训练算法，由于融合了现有技术中的深度生成网络模型以及本发明提出的条件极大矩匹配准则，因此，可有效地扩展基于矩匹配的深度生成模型的应用范围，使之能够应用于多样的任务例如根据类别的图像生成、数据分类、贝叶斯网络的指示提取等。

图3为本发明深度生成网络随机训练装置实施例的结构示意图，参看图3，本发明还提出一种深度生成网络随机训练装置，包括：输入单元1、分割单元2以及训练单元3。其中，所述输入单元1用于输入包括条件变量以及生成数据本身的数据集合；分割单元2用于将所述数据集合随机分割成包括一定数量样本的若干批次；训练单元3用于对各批次的样本数据通过梯度后向传播进行参数更新并输出所述参数；其中，所述对各批次的样本数据通过梯度后向传播进行参数更新包括使用条件极大矩匹配准则。

本发明提出的深度生成网络随机训练装置，由于在对样本数据的处理过程中使用了条件极大矩匹配准则，所述条件极大矩匹配准则是对MMD的拓展，因此，可扩展基于矩匹配的深度生成模型的应用范围。

具体地，所述输入单元1输入数据集合；例如输入数据集合其中，x_i为条件变量，y_i为生成数据本身；例如，对于一张被标记为类别A的图片，A即为条件变量x_i，图片为生成数据本身y_i。

所述分割单元2每次可从数据集合中随机用一个批次来近似整个数据集。所述批次的样本数量可根据数据集合的结构选取，具体地，对于结构简单的数据集，各批次包括的样本个数可以偏小，例如100-200。对于结构相对复杂的数据集，各批次的样本个数可适当增加。

所述训练单元3具体用于：

随机从输入数据集合D中选择一个批次B，对于任一x∈B，生成一个样本y；记B’为生成的数据集合(x,y)；

具体地，对于任一x∈B，其会与通过采样获得的隐式变量h组成向量组(x，h)。所述向量组通过网络传播生成样本y。

根据B与B’计算条件极大矩匹配准则

获取所述条件极大矩匹配准则关于参数的导数并以所述条件极大矩匹配准则关于参数的导数作为输出层的梯度；

根据链式求导法则获取各中间层的梯度；

对所述参数w通过梯度下降算法进行更新；

重复上述步骤直至所述参数w满足收敛条件后，输出所述参数w。

具体地，所述条件极大矩匹配准则(Conditional Maximum Mean Discreoancy，CMMD)包括：比较两个再生核希尔伯特空间之间算子的差异，以判断两个条件概率之间的差距。

具体地，所述条件极大矩匹配准则是MMD的推广，其通过比较两个再生核希尔伯特空间之间的算子的差异，以判断两个条件概率之间的差距。例如，设条件随机变量X，其对应的再生核希尔伯特空间为F；设另外两个条件随机变量Y，Z，两者对应的再生核希尔伯特空间都为G，则两个条件概率分别为P(Y|X)以及P(Z|X)。为对比上述两个条件概率，先将所述两个条件概率嵌入到希尔伯特空间中，可得两个希尔伯特空间之间的算子C_Y|X与C_Z|X，其也可看作是两个希尔伯特空间张量积形成的空间里的一个元素。所述条件极大矩匹配准则对比两个嵌入之间在空间所装备的范数意义下的差距：

$L_{CMMD}^2=\left|\right|C_{Y|X}-C_{Z|X}|{|}_{F\⊗G}^2$

实际应用中，设两个数据集与则可以比较两个概率嵌入估计的差值以近似L_CMMD：

${\hat{L}}_{CMMD}^2=\left|\right|{{\hat{C}}^s}_{Y|X}-{{\hat{C}}^d}_{Y|X}|{|}_{F\⊗G}^2$

其中，与分别是由两个数据集(即训练数据集与模型生成的数据集)生成的经验估计。一般地，条件概率的嵌入是无穷维的，但是通过核技巧，上述目标可以通过Kernel Gram矩阵高效地计算出来。对于连续变量，可选取高斯核函数；对于离散变量，可选择Delta核函数。具体地，核技巧通过将无线维的内积运算通过核函数准确地计算出来，因此有着可以实际计算的形式：

${\hat{L}}_{CMMD}^2=Tr(L_d\·C_1)+Tr(L_s\·C_2)+Tr(L_{ds}\·C_3)$

其中L是输出变量的Gram矩阵，C是由训练数据确定的参数矩阵。

在完成对当前批次的随机训练后，所述装置则重复上述步骤，直至完成对所述数据集合内的所有批次的随机训练。

本发明提供的深度生成网络随机训练装置，由于融合了现有技术中的深度生成网络模型以及本发明提出的条件极大矩匹配准则，因此，可有效地扩展基于矩匹配的深度生成模型的应用范围，使之能够应用于多样的任务例如根据类别的图像生成、数据分类、贝叶斯网络的指示提取等。

本发明在多项任务中取得了优秀的结果。在分类问题中，使用上述训练算法在手写数字MINST数据集分类错误率为0.9％，MINST数据集包含60,000个0-9手写数字，是一个10分类问题。此结果与当前最先进的分类器，例如Network in Network等相同。在另一个10分类问题SVHN数据集中取得了3.17％的错误率，SVHN包含了600,000个0-9的现实中的门牌编号照片。此结果同样与当前最先进的分类器可比。

在生成问题中，使用上述训练算法在MINST数据集上生成了高质量的样本。在人脸数据集Yale Face中，根据不同的人，生成了高质量的不同的图片。Yale Face数据集包含了38个不同人的脸部特写，训练数据总共2,414张图片。

在贝叶斯网络的知识提取任务中，使用上述训练算法在Boston Housing数据集上的结果为几乎没有性能损失。具体而言，Boston Housing包含了506个13维的数据，目标是根据数据进行预测。实验首先训练一个贝叶斯网络PBP来进行预测，之后用本发明训练算法进行知识提取。PBP网络的预测在均方误差的度量下均值为2.574，而经过提取之后均值为2.580，几乎没有性能损失。

最后应说明的是：以上实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的精神和范围。