基于素数标记的有圈图小枝存在性查询方法与流程

本发明涉及一种基于素数标记的有圈图小枝存在性查询方法，更具体的说，尤其涉及一种首相将有圈图转换为有向无圈图再根据小枝中节点类别和边的要求进行查找的基于素数标记的有圈图小枝存在性查询方法。

背景技术：

图论以图为研究对象，图由若干给定的点及连接两点的线所构成的图像，是解决复杂工程问题常用的数学理论和工具。图论中，用点代表事物，用连接两点的线表示相应两个事物间具有的关系。

基于区间标记的方法是树形结构图中用的较广的方法。其思想是对树T中的每个节点标记一个区间[s,e]。根据前序遍历法所构建的区间有一个重要的特点，即如果节点u可达节点v，则u的区间[su,eu]包含v的区间[sv,ev]。然而区间标记法不支持有圈图。

素数标记法也可以支持小枝存在性查询。其思想是为图中的每个节点赋一个素数或素数的乘积，使得若节点u是节点v的祖先，u的素数标记可以被v的素数标记整除。素数标记法可以支持有圈图的查询，但要求用到大量的素数。而众所周知，大素数生成是非常耗时的，因此效率较低。

DataGuide方法构建一个模型来描述G中所有的路径。DataGuide的思想是把图G看做一个不确定性自动机，并根据自动机理论用多个确定性自动机来描述一个不确定性自动机。然而DataGuide需要指数数量的确定性自动机来准确描述一个不确定自动机。

Straight-Line Grammar构建语法树来支持存在性查询。Straight-Line Grammar是上线文无关文法的特殊形式。Straight-Line Grammar的思想是用通配符来表达文法中的非终结符。然而该方法的效率较低。

XSketch是构建G的一个概要图。XSketch的思想是找出G中重复出现的部分，将多个部分进行合并成一个，这样能节省查询时的重复计算，降低计算量。然而XSketch仅支持无分支路径查询。

故，现有的查询方法不支持有圈图查询或不支持小枝查询，而且查询效率十分低下。

技术实现要素：

本发明为了克服上述技术问题的缺点，提供了一种基于素数标记的有圈图小枝存在性查询方法。

本发明的基于素数标记的有圈图小枝存在性查询方法，其特别之处在于，通过以下步骤来实现：

a).标记有圈图、小枝，将有圈图标记为G，设有圈图G中的节点数为n，n个节点分别标记为v1、v2、...、vn，其类别分别标记为kindv1、kindv2、...、kindvn；将待查询的小枝标记为T，设小枝T中的节点数为k，k个节点分别标记为u1、u2、...、uk，其类别分别标记为kindu1、kindu2、...、kindun，k、n均为正整数；不同节点可为同一类别；

b).将有圈图转换为无圈图，按照“有圈图G中的一个强连通分量变为有向无圈图中的一个节点，且变为节点的类别为强连通分量中各节点类别的并集”的原则，从有圈图G中提取强连通分量，把有圈图G转换为一个有向无圈图G′；设转换后的有向无圈图G′有m个节点，m个节点分别为v1′、v2′、...、vm′，m为正整数，m＜n；

c).素数标记，先对有向无圈图G′中的节点进行素数标记，然后在根据“有圈图G的同一个强连通分量的节点赋相同素数标记”的原则对有圈图G中的节点进行素数标记；

d).根据类别信息查找匹配节点，根据小枝T中节点ui的类别kindui，从有向无圈图G′中查找出与类别kindui一致的节点，并将节点ui与查找出的节点建立对应；直至小枝T中所有节点查找完毕；

e).根据小枝T中边的要求进行筛选，按照小枝T中各单跳边、多跳边以及孩子节点、父亲节点对有向无圈图G′中节点类别的要求，判断步骤d)中查找的节点是否满足要求，如果满足要求，则表明有圈图G中存在小枝T；如果不满足要求，则表明有圈图G中不存在小枝T。

本发明的基于素数标记的有圈图小枝存在性查询方法，步骤c)中所述的素数标记按照如下步骤实现：

c-1).对G′进行素数标记：

c-1-1).叶子节点赋素数，首先将有向无圈图G′中的每个叶子节点赋一个不同的素数；

c-1-2).父亲节点赋素数，如果父亲节点u的所有孩子节点均存在另一个父亲节点，则把u的所有孩子的素数标记进行乘积，再乘以一个新的素数，将最后的乘积赋给u；否则，将u的所有孩子的素数标记进行乘积，将乘积赋给u；

c-2).对G进行素数标记：

c-2-1).若G中的节点u在G′中是一个独立的节点u′，则直接把u′的素数标记赋给u；

c-2-2).若G中的节点u在G′中是一个强连通分量缩变成的节点u′，则直接把u′的素数标记赋给u。

本发明的有益效果是：本发明的基于素数标记的有圈图小枝存在性查询方法，首先将有圈图转化为有向无圈图，再利用“叶子节点赋一个不同的素数、父亲节点赋孩子素数乘积或孩子素数与新素数乘积”的形式对有向无圈图中各节点进行素数标记；在小枝查询的过程中，首先根据小枝节点中节点的类别查询出符合要求的节点，再根据小枝中单跳边、多跳边以及孩子节点、父亲节点对节点类别的要求，进行进一步筛选，以判断有圈图中是否存在所要查找的小枝，解决了现有的查询方法不支持有圈图查询或不支持小枝查询的问题。

本发明的基于素数标记的有圈图小枝存在性查询方法的优点体现在：

(1)本发明所提出的素数标记法所需要的素数大大小于现有的素数标记法，一方面大大减少了素数标记的空间开销，另一方面大大减少了素数生成所需的时间开销。

(2)本发明能支持有圈图上的小枝查询，而现有的方法要么不支持有圈图，要么不支持小枝查询，本发明拓宽了小枝查询的应用范围。

附图说明

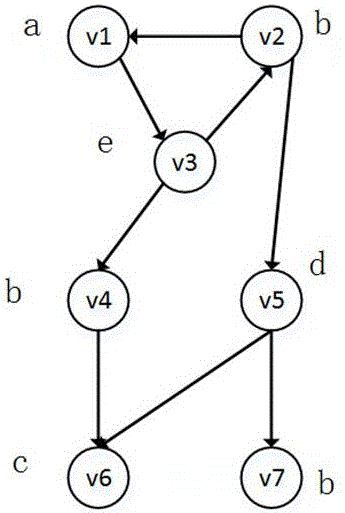
图1为本发明的实施例中有圈图G；

图2为本发明的实施例中待查询的小枝T；

图3为本发明的实施例中有圈图G转换为的有向无圈图G′；

图4为本发明的实施例中有向无圈图G′进行素数标记后的示意图。

具体实施方式

下面结合附图与实施例对本发明作进一步说明。

如图1所示，给出了本发明的实施例中有圈图G，有圈图G中包含的节点分别为v1、v2、v3、v4、v5、v6、v7，其类别分别为a、b、e、b、d、c、b。如图2所示，给出了本发明的实施例中待查询的小枝T，小枝T中包含的节点分别为u1、u2、.u3、u4，其类别分别为a、b、c、d。

如图3所示，给出了有圈图G转换为的有向无圈图G′，图1中有圈图G中的三个节点v1、v2、v3为G的一个强连通分量，合并为有向无圈图G′的一个节点v1′。v1′节点的类别是v1、v2、v3三个节点类别的并集a、b、e。有圈图G中的v1、v2、v3的素数标记等于有向无圈图G′中v1′的素数标记。有圈图G转换为的有向无圈图G′中，节点分别为v1′、v2′、v3′、v4′、v5′，其类别分别为a、b、e，b，c，e，b。

如图4所示，给出了有向无圈图G′进行素数标记后的示意图，对有向无圈图G′进行素数标记进行素数标记过程中，叶子节点v3′、v5′分别赋予素数3、5；在无圈图G′中，父亲节点v2′只有v3′节点一个孩子，但是v3′节点有2个父亲(v2′和v4′)，所以父亲节点v2′的素数标记需要引入一个新的素数(素数7)。父亲节点v4′有两个孩子v3′节点和v5′节点，但不是所有的孩子都有多个父亲(节点v5′只有一个父亲v4′)，所以v4′的素数标记为v4′的孩子(v3′、v5′)的素数标记的乘积即可。同理，父亲节点v1′标记为孩子节点v2′和v4′的素数标记的乘积。

在查询有向无圈图G′是否存在小枝T的过程中，首先根据类别信息，找出小枝T中的节点和有向无圈图G′中的节点的匹配关系。例如小枝T中u1的类别为a，它对应到G′中所有类别为a的节点。即u1对应v1′；u2的类别为b，它对应到G′中的v2′和v5′。u3的类别为c，它对应到G′中的节点v3′；u4的类别为d，它对应到G′中的节点v4′。

然后，根据小枝T中边的要求，对上面匹配的节点进行筛选。具体如下：小枝T总要求类别a的u1和类别b的u2要有多跳可达关系，而G′中的v2′和v5′都满足该要求；小枝T中要求类别b的u2要有一个类别为c的孩子，则只有v2′满足该要求；小枝T中要求类别为c的节点要有一个类别为d的父亲，则v3′和v4′可满足该要求，筛选完毕后，可见有圈图G中是存在小枝T的。