一种建筑物不同参数对大气电场畸变效应的数值模拟方法与流程

本发明涉及一种建筑物不同参数对大气电场畸变效应的数值模拟方法，属于雷电监测预警技术领域。

背景技术：

雷暴是指积雨云中发生的雷电交作的激烈放电现象，作为一种局地强对流天气现象，常与暴雨、大风、冰雹、龙卷风等灾害性天气联系在一起，近年来，关于雷电对人民生命财产安全构成算严重的威胁，因此雷暴监测预警工作尤为重要。大气电场仪是雷暴监测预警系统的重要组成部分，由于大气电场仪安装的位置周围有建筑物存在，建筑物对大气电场具有一定的畸变效应，因此需要对建筑物大气电场的畸变效应进行研究，从而对大气电场仪的安装位置进行场地修订，能够提高雷电监测预警的准确性。

就目前，对建筑物参数不同针对大气电场畸变效应数值的影响的相关研究较少，且不够完善、系统，急需对相关的内容进行研究，得到完善的结论，能够有效地对大气电场仪的修订以及对雷暴检测预警工作的展开提供科学指导。

技术实现要素：

针对现有技术存在的不足，本发明目的是提供一种建筑物不同参数对大气电场畸变效应的数值模拟方法，通过对建筑物大气电场的畸变效应进行数值模拟，以便能够对大气电场仪的测量数据进行修订，能够提高雷电监测预警的准确性。

为了实现上述目的，本发明是通过如下的技术方案来实现：

本发明的一种建筑物不同参数对大气电场畸变效应的数值模拟方法，包括以下步骤：

(1)利用有限差分方法求出建筑物大气电场的畸变系数，用于对大气电场仪的实际测量值进行修订；

所述有限差分方法具体方法如下：

对所研究的空间模拟域进行离散化处理，满足泊松方程的二维电场基本表达式如下：

式中，ρ为所研究区域的自由电荷密度值，ε为介电常数，为所研究区域的电势；如果所研究的空间模拟域内没有自由电荷的影响下，上述公式中取ρ＝0，则上述泊松方程就等效成拉普拉斯方程：

然后将上述等效后的拉普拉斯方程写成在直角坐标系的表达形式：

然后采用五点差分的格式，对所研究的空间模拟域进行离散化处理，假设在空间尺度上x和y方向上的网格部分的步长均相等，步长值均为h,因子所模拟的空间场域内的差分方程表达式为：

其中，i为x方向的格点数，j为y方向的格点数；如i＝1即x方向的第1个格点，j＝2即y方向的第2个格点；

然后，将方程(2)和(3)公式带入差分后的方程(4)中得到：

最后，考虑建筑物所在的空间模拟区域的一系列边界条件，对方程(5)计算，就可以求出离散化后的空间范围内每一个格点的电位值；

(2)对每一个格点的电位值进行计算，在计算的过程中，i,j是按照从小到大的原则进行计算的，然后进行迭代，迭代到设定的一个空间位置时，计算出新的对方程(5)采用超松弛迭代算法，并将方程改写成：

其中，n为迭代次数，ω为超松弛迭代因子，利用方程(6)就可以计算出，整个空间模拟域内的每一个格点上的电位值，然后通过所求出的电位值计算出格点上的电场强度，电场强度与电位之间的关系表达式为：

即电场强度等于负的电位的梯度；

将格点上的电场强度值与所研究的空间模拟域的背景电场值之比，即畸变系数。

步骤(1)中，模拟域的上边界以及左右边界满足Neumann边界条件，地面以及建筑物表面满足Dirichlet边界条件。

上述超松弛迭代因子ω的取值为1<ω<2。

与现有技术相比，本发明具有的有益效果是：通过有限差分方法分别研究单个建筑物的高度、宽度以及多个建筑物的高度、宽度对大气电场畸变效应的数值模拟，并求出畸变系数，用于对大气电场仪的实际测量值进行修订，能够提高雷电监测预警的准确性。

附图说明

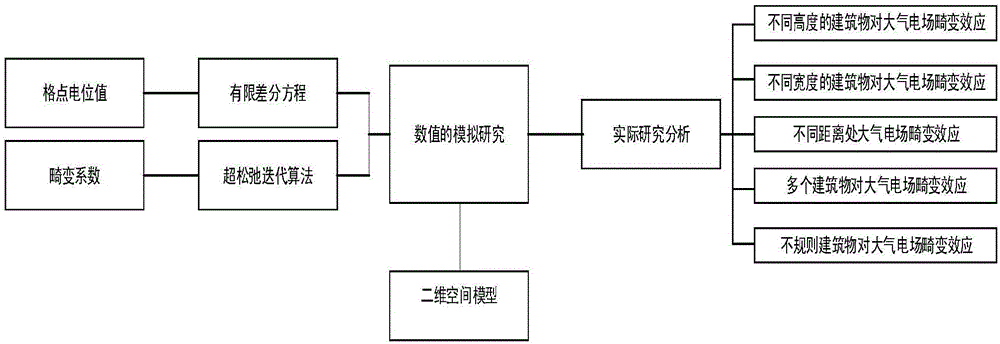
图1为本发明的结构框图；

图2为模拟域空间结构图；

图3(a)为建筑物高度为20m时对大气电场畸变效应模拟结果；

图3(b)为建筑物高度为25m时对大气电场畸变效应模拟结果；

图3(c)为建筑物高度为30m时对大气电场畸变效应模拟结果；

图3(d)为建筑物高度为35m时对大气电场畸变效应模拟结果；

图4为建筑物不同高度下的畸变系数以及线性拟合结果；

图5(a)为建筑物宽度取值为5m时对大气电场畸变效应模拟结果；

图5(b)为建筑物宽度取值为7m时对大气电场畸变效应模拟结果；

图5(c)为建筑物宽度取值为9m时对大气电场畸变效应模拟结果；

图5(d)为建筑物宽度取值为11m时对大气电场畸变效应模拟结果；

图6为建筑物不同宽度下的畸变系数以及线性拟合结果；

图7(a)为大气电场仪安装位于距离建筑物建取值为2m时对大气电场畸变效应模拟结果；

图7(b)为大气电场仪安装位于距离建筑物建取值为4m时对大气电场畸变效应模拟结果；

图7(c)为大气电场仪安装位于距离建筑物建取值为8m时对大气电场畸变效应模拟结果；

图7(d)为大气电场仪安装位于距离建筑物建取值为16m时对大气电场畸变效应模拟结果；

图8地面电场仪安装位置与建筑物之间不同距离下的畸变系数以及线性拟合结果；

图9(a)大气电场仪安装在高度分别为35m、45m，宽度分别为10m、10m的两个建筑物建之间时大气电场畸变效应模拟结果；

图9(b)大气电场仪安装在高度分别为35m、70m，宽度分别为10m、10m的两个建筑物建之间时大气电场畸变效应模拟结果；

图9(c)大气电场仪安装在高度分别为35m、45m，宽度分别为10m、6m的两个建筑物建之间时大气电场畸变效应模拟结果；

图9(d)大气电场仪安装在高度分别为35m、70m，宽度分别为10m、6m的两个建筑物建之间时大气电场畸变效应模拟结果；

图10(a)为大气电场仪安装在复杂度低的不规则建筑物旁边时大气电场畸变效应模拟结果；

图10(b)为大气电场仪安装在复杂度高的不规则建筑物旁边时大气电场畸变效应模拟结果。

具体实施方式

为使本发明实现的技术手段、创作特征、达成目的与功效易于明白了解，下面结合具体实施方式，进一步阐述本发明。

本发明在研究建筑物对大气电场造成的畸变效应研究时，需要求出其畸变系数表示为求出的格点上的电场强度值与所研究的空间模拟域的背景电场值的比值。提供一种建筑物不同参数对大气电场畸变效应的数值，通过对建筑物大气电场的畸变效应进行数值模拟，以便能够对大气电场仪的实际测量结果进行修订。

参见图1，有限差分的方法最主要的思想就是将所研究的空间模拟域进行离散化处理，本发明可以使用有限差分对此类电磁学问题进行求解。满足泊松方程的二维电场基本表达式如下：

式中，ρ为所研究区域的自由电荷密度值，ε为介电常数，为所研究区域的电势。如果所研究的空间模拟域内没有自由电荷的影响下，上述公式中取ρ＝0，则上述泊松方程就等效成拉普拉斯方程：

然后将上述等效后的拉普拉斯方程写成在直角坐标系的表达形式：

对于二维问题，本文然后采用五点差分的格式，对所研究的空间模拟域进行离散化处理，本文假设在空间尺度上x和y方向上的网格剖分的步长均相等，步长值均为h,因子所模拟的空间场域内的差分方程表达式为：

然后将方程(2)和(3)公式带入差分后的方程(4)中得到：

最后在考虑建筑物所在的空间模拟区域的一些列边界条件，对方程(5)计算，就可以求出离散化后的空间范围内每一个格点的电位值。

本发明在对大气电场畸变效应的计算工程中，对模拟的空间场域进行了离散划分，然后对每一个格点的电场值进行计算，在计算的过程中，i,j是按照从小到大的原则进行计算的，然后进行迭代，迭代到某一个空间位置时，计算出新的对方程(5)采用超松弛迭代算法，并将方程改写成：

为了保证计算过程中迭代的收敛性，通常对超松弛迭代因子取值为1<ω<2。利用方程(6)就可以计算出，整个空间模拟域内的每一个格点上的电位值，然后通过所求出的电位值计算出格点上的电场强度，电场强度与电位之间的关系表达式为：

即电场强度等于负的电位的梯度。本文在研究建筑物对大气电场造成的畸变效应研究时，需要求出其畸变系数可以表示为求出的格点上的电场强度值与所研究的空间模拟域的背景电场值的比值。

本发明在对大气电场的畸变效应的研究工作中，建立了二维空间模拟域，空间域的大小为300m×100m，本文对空间模拟域的背景电场取值为晴天大气电场的均值，即130V/m，晴天大气电场方向垂直指向地面，且该研究空间模拟域内没有其它自由电荷的影响，且假设建筑物的表面与地面呈等电势分布，即电势取值为0。图2为模拟域的空间结构图，图中W为建筑物的宽度，H为建筑物高度。对空间模拟域的边界条件设置为，模拟域的上边界以及左右边界满足Neumann边界条件；地面以及建筑物表面满足Dirichlet边界条件。所研究区域的空间模拟域的空间分辨率为，即空间采取离散化后所剖分出的网格总数为(300/h)*(100/h)。

本发明首先研究在建筑物宽度一定时，不同建筑物的高度对大气电场的畸变效应的影响。所选取的建筑物的宽度为20m，然后分别选取建筑物的高度为20m,25m,30m,35m这四种情况，空间模拟域的尺寸均为300m×100m。大气电场仪安装在建筑物的顶端，电场仪的高度取值为0.5m，宽度取值为0.08m，且模拟区域内无其它自由电荷。利用matlab软件，编写出上文中所描述的满足一定边界条件下对泊松方程进行求解的程序。图3(a)、(b)、(c)、(d)为建筑物高度分别为20m、25m、30m、35m时对大气电场畸变效应模拟结果，从图中可以看出，如果模拟区域没有建筑物时，大气电场应该呈一条等势线，当模拟区域存在建筑物时，建筑物会对大气电场造成一定的畸变效应，且等值线越密集的地方，建筑物对大气电场造成的畸变效应就越显著。当空间模拟域内建筑物的高度为20m时，求出的大气电场畸变系数为2.0091；当建筑物高为25m时，求出的大气电场畸变系数为2.2610；当建筑物高为30m时，求出的大气电场畸变系数为2.5125；当建筑物高为30m时，求出的大气电场畸变系数为2.7638，可以看出，随着建筑的高度逐渐增高时，电场仪顶端处的大气电场畸变系数也随之逐渐增大。

表1建筑物不同高度下的大气电场畸变系数

表1统计出了建筑高度取值范围在20m-90m之间时的大气电场畸变系数统计结果，可以看出在不同高度下，大气电场畸变系数均大于1，进一步说明了建筑物均会对大气电场造成一定的畸变效应。其中，还可以看出，大气电场畸变系数与建筑物高度之间存在一定的正相关性关系，即建筑物越高，大气电场畸变系数值也就越大。对表1中计算出的畸变系数结果，进行曲线拟合，拟合结果如图4所示，从图中可以看出，大气电场畸变系数与建筑物的高度之间存在显著的一元线性关系，拟合出的一元直线方程为y＝0.0502*x+1.0058，方程中的x为建筑物的高度，y为大气电场畸变系数，可以看大气电场畸变系数随着x取值的增加呈现出线性递增的变化趋势。因此，如果想要求出本文研究高度范围(20m-90m)之外的大气电场畸变系数值时，只要将建筑物高度值带入上述拟合出来的方程即可。

本发明其次研究在建筑物高度一定时，研究不同建筑物的宽度对大气电场的畸变效应的影响。所选取的建筑物的高度为35m，然后分别选取建筑物的宽度为5m,7m,9m,11m这四种情况，空间模拟域的尺寸均为300m×100m。大气电场仪安装在建筑物的顶端中间位置处，电场仪的高度取值为0.5m，宽度取值为0.08m，且模拟区域内任然无其它自由电荷。利用matlab软件，编写出上文中所描述的满足一定边界条件下对泊松方程进行求解的程序。图5(a)、(b)、(c)、(d)为建筑物高度一定时，宽度分别取值为5m、7m、9m、11m时对大气电场畸变效应模拟结果，从图中可以直观的看出，建筑物的宽度取值不一样时，对大气电场造成的畸变效应也不相同，其中建筑物宽度取值越小时，对大气电场造成的畸变效应越显著。当空间模拟域内建筑物的宽度取值为5m时，求出的大气电场畸变系数为4.9525；当建筑物宽度取值为7m时，求出的大气电场畸变系数为4.2000；当建筑物宽度取值为9m时，求出的大气电场畸变系数为3.7511；当建筑物宽度取值为11m时，求出的大气电场畸变系数为3.4521，可以看出，随着建筑的宽度逐渐增高时，大气电场的畸变系数随之逐渐减小，在建筑物的顶端等势线越密集的地方，造成的畸变效应越显著，电场值的大小，等于该位置处的电势的梯度。距离地面越高处的等势线，就越平行于地面。

表2建筑物不同宽度下的大气电场畸变系数

表2统计出了建筑宽度取值范围在5m-33m之间时的大气电场畸变系数统计结果，可以看出在不同建筑物宽度取值下，大气电场畸变系数均大于1，进一步说明了建筑物宽度取值均会对大气电场造成一定的畸变效应。其中，还可以看出，大气电场畸变系数与建筑物宽度之间存在一定的负相关性关系，即建筑物越宽，大气电场畸变系数值就越小。对表2中计算出的畸变系数结果，进行曲线拟合，拟合结果如图6所示，从图中可以看出，大气电场畸变系数与建筑物的宽度之间为非线性的关系，呈现出了二次曲线的关系，拟合出的二元曲线方程为y＝0.0007*x²-0.1030*x+6.4071，方程中的x为建筑物的宽度，y为大气电场畸变系数，可以看大气电场畸变系数随着x取值的增加呈现非线性递减的变化趋势。且在建筑物宽度为5m-7m之间，随着建筑物宽度的增加，大气电场畸变系数呈显著性的递减趋势，从建筑物的宽度增加至7m之后，随着建筑物宽度的继续增加，大气电场畸变系数递减的幅度较小。此外，如果想要求出本文研究宽度范围(5m-33m)之外的大气电场畸变系数值时，只要将建筑物宽度值带入上述拟合出来的二元曲线方程即可。

本发明继续研究在建筑物尺寸一定时，研究大气电场仪安装位置距离建筑物不同距离处时的大气电场的畸变效应。所选取的建筑物的高度为35m，宽度为20m。大气电场仪安装在地面上，电场仪的高度取值为0.5m，宽度取值为0.08m，然后分别选取大气电场仪安装位置与建筑物之间的距离分别取值为2m,4m,8m,16m这四种情况，空间模拟域的尺寸均为300m×100m。图7(a)、(b)、(c)、(d)为大气电场仪安装位于距离建筑物建分别取值2m、4m、8m、16m时对大气电场畸变效应模拟结果，从图中可以看出，当大气电场仪安装的位置周围有建筑物存在时，建筑物会对电场仪形成一种屏蔽的作用，计算出的大气电场仪安装在建筑物附近时的电场仪顶端的大气电场畸变系数均小于1，这主要是由于建筑物的屏蔽作用引起的，由于屏蔽作用的影响，从而使得大气电场仪的实测测量值偏小。当地面电场仪安装位置距离建筑物的距离取值为2m时，求出的电场仪顶端的大气电场畸变系数为0.0450；当地面电场仪安装位置距离建筑物的距离取值为4m时，求出的电场仪顶端的大气电场畸变系数为0.1794；当地面电场仪安装位置距离建筑物的距离取值为8m时，求出的电场仪顶端的大气电场畸变系数为0.4204；当地面电场仪安装位置距离建筑物的距离取值为16m时，求出的电场仪顶端的大气电场畸变系数为0.8282。

表3电场仪距离建筑物不同距离处时的大气电场畸变系数

表3统计出了地面电场仪安装位置与建筑物之间水平距离取值范围在2m-16m之间时的电场仪顶端处的大气电场畸变系数统计结果，可以看出在距离建筑物不同的位置处，计算出的地面大气电场仪顶端出的大气电场畸变系数均小于1，通常情况下，电场仪安装位置周围无其它建筑物时，计算出的电场仪顶端的畸变系数为1，从表格中的统计数据可以进一步说明了，建筑物会对安装在其周围的电场仪形成一种屏蔽作用，从而使得电场仪的实测测量值存在很大的误差，在越靠近建筑物的地方，大气电场畸变系数值就越小，越远离建筑物的地方，畸变系数值就越大，主要是建筑物对较远处的屏蔽效应较小。

对表3中计算出的畸变系数结果，进行曲线拟合，拟合结果如图8所示，图8为地面电场仪安装位置与建筑物之间不同距离下的畸变系数以及线性拟合结果，从图中可以看出，地面电场仪距离建筑物的水平距离与电场仪顶端的大气电场畸变系数之间存在正相关性的关系，即电场仪距离建筑物越远时，畸变系数值就越大。可以看出地面电场仪距离建筑物的水平距离与电场仪顶端的大气电场畸变系数之间为线性关系，拟合出的一元直线方程为y＝0.0559*x-0.0397，方程中的x为地面电场仪与建筑物之间的水平距离，y为电场仪顶端大气电场畸变系数，从方程可以直观地看出，大气电场畸变系数随着x取值的增加呈现线性递增的变化趋势。此外，如果想要求出本文研究宽度范围(2m-16m)之外的大气电场畸变系数值时，只要将地面电场仪与建筑物之间的水平距离值带入上述拟合出来的一元直线方程即可。

多个建筑物对大气电场畸变效应,当地面电场仪周围有两个或者多个建筑物存在时，多个建筑物必然会对电场仪的造成一种屏蔽作用，因此有必要研究多个建筑物对地面大气电场的畸变效应。本发明选取的空间模拟域的尺寸均为300m×100m，且模拟区域内任然无其它自由电荷。大气电场仪安装在水平地面上，且在电场仪两侧各有一栋建筑物楼层，分别模拟了4组不同楼层高度下的大气电场畸变效应。第一组情况为：地面电场仪左边的建筑物高度为35m,建筑物宽度为10m,建筑物距离电场仪水平距离为25m,地面电场仪右边的建筑物高度为45m,建筑物宽度为10m,建筑物距离电场仪水平距离为20m。第二组情况为：地面电场仪左边的建筑物尺寸同第一组设定的情况,地面电场仪右边的建筑物高度为70m,建筑物宽度为10m,建筑物距离电场仪水平距离为20m。第三组情况为：地面电场仪左边的建筑物尺寸同第一组设定的情况,地面电场仪右边的建筑物高度为45m,建筑物宽度为6m,建筑物距离电场仪水平距离为22m。第四组情况为：地面电场仪左边的建筑物尺寸同第一组设定的情况,地面电场仪右边的建筑物高度为70m,建筑物宽度为6m,建筑物距离电场仪水平距离为22m。

图9(a)、(b)、(c)、(d)为大气电场仪安装在不同尺寸下的两个建筑物建之间时大气电场畸变效应模拟结果，从图中可以看出，不同的建筑物尺寸对大气电场畸变的效应是不相同，但总体来说，等值线越密集的地方，建筑物对大气电场造成的畸变效应就越显著，在垂直距离远离建筑的地方越远处的大气电场等势线就越平行于地面。对于第一种情况，我们运用matlab软件计算出的对安装在这两种尺寸建筑物之间的电场仪顶端的畸变系数值为0.8303，畸变系数小于1，主要是由于建筑物的屏蔽效应造成的；第二组情况，只改变了右侧建筑物的高度，计算出的电场仪顶端的大气电场畸变系数值也为0.8303，这说明了在左侧建筑物尺寸不变的情况下，只改变右侧建筑物的高度，计算出的电场畸变值是相同的，这可能主要是由于电场仪距离左侧建筑物较近，电场仪处于左侧建筑物的屏蔽范围之内；对于第三组情况，计算的电场仪顶端处的电场畸变系数为0.8644，这个畸变结果要大于第一、二组的情况，主要是第三组实验缩小了右侧建筑物的宽度，越窄的建筑物对大气电场造成的畸变效应越显著；第四组情况下计算出的电场仪顶端处的电场畸变系数也为0.8644。

本发明继续研究了当大气电场仪安装在不规则建筑旁边时建筑物对大气电场畸变效应的影响，以及对地面电场仪的屏蔽效应。图10(a)、(b)为大气电场仪安装在不规则建筑物旁边时大气电场畸变效应模拟结果，从图中可以看出，在建筑物越尖端处大气电场畸变效应越显著，图中模拟了两种复杂建筑物情况，计算出的复杂建筑物对地面大气电场仪的畸变系数分别为0.4611,0.4453。

以上显示和描述了本发明的基本原理和主要特征和本发明的优点。本行业的技术人员应该了解，本发明不受上述实施例的限制，上述实施例和说明书中描述的只是说明本发明的原理，在不脱离本发明精神和范围的前提下，本发明还会有各种变化和改进，这些变化和改进都落入要求保护的本发明范围内。本发明要求保护范围由所附的权利要求书及其等效物界定。